Statistics

• 1.I.3D

  Statistics

  Part IB, 2001

  Let $X_{1}, \ldots, X_{n}$ be independent, identically distributed $N\left(\mu, \mu^{2}\right)$ random variables, $\mu>0$.

  Find a two-dimensional sufficient statistic for $\mu$, quoting carefully, without proof, any result you use.

  What is the maximum likelihood estimator of $\mu$ ?

  comment

• 1.II.12D

  Statistics

  Part IB, 2001

  What is a simple hypothesis? Define the terms size and power for a test of one simple hypothesis against another.

  State, without proof, the Neyman-Pearson lemma.

  Let $X$ be a single random variable, with distribution $F$. Consider testing the null hypothesis $H_{0}: F$ is standard normal, $N(0,1)$, against the alternative hypothesis $H_{1}: F$ is double exponential, with density $\frac{1}{4} e^{-|x| / 2}, x \in \mathbb{R}$.

  Find the test of size $\alpha, \alpha<\frac{1}{4}$, which maximises power, and show that the power is $e^{-t / 2}$, where $\Phi(t)=1-\alpha / 2$ and $\Phi$ is the distribution function of $N(0,1)$.

  [Hint: if $X \sim N(0,1), P(|X|>1)=0.3174 .]$

  comment

• 2.I.3D

  Statistics

  Part IB, 2001

  Suppose the single random variable $X$ has a uniform distribution on the interval $[0, \theta]$ and it is required to estimate $\theta$ with the loss function

  $$L(\theta, a)=c(\theta-a)^{2}$$

  where $c>0$.

  Find the posterior distribution for $\theta$ and the optimal Bayes point estimate with respect to the prior distribution with density $p(\theta)=\theta e^{-\theta}, \theta>0$.

  comment

• 2.II.12D

  Statistics

  Part IB, 2001

  What is meant by a generalized likelihood ratio test? Explain in detail how to perform such a test

  Let $X_{1}, \ldots, X_{n}$ be independent random variables, and let $X_{i}$ have a Poisson distribution with unknown mean $\lambda_{i}, i=1, \ldots, n$.

  Find the form of the generalized likelihood ratio statistic for testing $H_{0}: \lambda_{1}=\ldots=\lambda_{n}$, and show that it may be approximated by

  $$\frac{1}{\bar{X}} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2},$$

  where $\bar{X}=n^{-1} \sum_{i=1}^{n} X_{i}$.

  If, for $n=7$, you found that the value of this statistic was $27.3$, would you accept $H_{0}$ ? Justify your answer.

  comment

• 4.I.3D

  Statistics

  Part IB, 2001

  Consider the linear regression model

  $$Y_{i}=\beta x_{i}+\epsilon_{i},$$

  $i=1, \ldots, n$, where $x_{1}, \ldots, x_{n}$ are given constants, and $\epsilon_{1}, \ldots, \epsilon_{n}$ are independent, identically distributed $N\left(0, \sigma^{2}\right)$, with $\sigma^{2}$ unknown.

  Find the least squares estimator $\widehat{\beta}$ of $\beta$. State, without proof, the distribution of $\widehat{\beta}$ and describe how you would test $H_{0}: \beta=\beta_{0}$ against $H_{1}: \beta \neq \beta_{0}$, where $\beta_{0}$ is given.

  comment

• 4.II.12D

  Statistics

  Part IB, 2001

  Let $X_{1}, \ldots, X_{n}$ be independent, identically distributed $N\left(\mu, \sigma^{2}\right)$ random variables, where $\mu$ and $\sigma^{2}$ are unknown.

  Derive the maximum likelihood estimators $\widehat{\mu}, \widehat{\sigma}^{2}$ of $\mu, \sigma^{2}$, based on $X_{1}, \ldots, X_{n}$. Show that $\widehat{\mu}$ and $\widehat{\sigma}^{2}$ are independent, and derive their distributions.

  Suppose now it is intended to construct a "prediction interval" $I\left(X_{1}, \ldots, X_{n}\right)$ for a future, independent, $N\left(\mu, \sigma^{2}\right)$ random variable $X_{0}$. We require

  $$P\left\{X_{0} \in I\left(X_{1}, \ldots, X_{n}\right)\right\}=1-\alpha$$

  with the probability over the joint distribution of $X_{0}, X_{1}, \ldots, X_{n}$.

  Let

  $$I_{\gamma}\left(X_{1}, \ldots, X_{n}\right)=\left(\widehat{\mu}-\gamma \widehat{\sigma} \sqrt{1+\frac{1}{n}}, \widehat{\mu}+\gamma \widehat{\sigma} \sqrt{1+\frac{1}{n}}\right)$$

  By considering the distribution of $\left(X_{0}-\widehat{\mu}\right) /\left(\widehat{\sigma} \sqrt{\frac{n+1}{n-1}}\right)$, find the value of $\gamma$ for which $P\left\{X_{0} \in I_{\gamma}\left(X_{1}, \ldots, X_{n}\right)\right\}=1-\alpha .$

  comment

• $1 . \mathrm{I} . 3 \mathrm{H} \quad$

  Statistics

  Part IB, 2002

  State the factorization criterion for sufficient statistics and give its proof in the discrete case.

  Let $X_{1}, \ldots, X_{n}$ form a random sample from a Poisson distribution for which the value of the mean $\theta$ is unknown. Find a one-dimensional sufficient statistic for $\theta$.

  comment

• 1.II.12H

  Statistics

  Part IB, 2002

  Suppose we ask 50 men and 150 women whether they are early risers, late risers, or risers with no preference. The data are given in the following table.

  $\begin{array}{lcccc} & \text { Early risers } & \text { Late risers } & \text { No preference } & \text { Totals } \\ \text { Men } & 17 & 22 & 11 & 50 \\ \text { Women } & 43 & 78 & 29 & 150 \\ \text { Totals } & 60 & 100 & 40 & 200\end{array}$

  Derive carefully a (generalized) likelihood ratio test of independence of classification. What is the result of applying this test at the $0.01$ level?

  $\left[\begin{array}{lccccc}\text { Distribution } & \chi_{1}^{2} & \chi_{2}^{2} & \chi_{3}^{2} & \chi_{5}^{2} & \chi_{6}^{2} \\ 99 \% \text { percentile } & 6.63 & 9.21 & 11.34 & 15.09 & 16.81\end{array}\right]$

  comment

• $2 . \mathrm{I} . 3 \mathrm{H} \quad$

  Statistics

  Part IB, 2002

  Explain what is meant by a uniformly most powerful test, its power function and size.

  Let $Y_{1}, \ldots, Y_{n}$ be independent identically distributed random variables with common density $\rho e^{-\rho y}, y \geq 0$. Obtain the uniformly most powerful test of $\rho=\rho_{0}$ against alternatives $\rho<\rho_{0}$ and determine the power function of the test.

  comment

• 2.II.12H

  Statistics

  Part IB, 2002

  For ten steel ingots from a production process the following measures of hardness were obtained:

  $$73.2, \quad 74.3, \quad 75.4, \quad 73.8, \quad 74.4, \quad 76.7, \quad 76.1, \quad 73.0, \quad 74.6, \quad 74.1 .$$

  On the assumption that the variation is well described by a normal density function obtain an estimate of the process mean.

  The manufacturer claims that he is supplying steel with mean hardness 75 . Derive carefully a (generalized) likelihood ratio test of this claim. Knowing that for the data above

  $$S_{X X}=\sum_{j=1}^{n}\left(X_{i}-\bar{X}\right)^{2}=12.824$$

  what is the result of the test at the $5 \%$ significance level?

  $\left.\begin{array}{lll}{[\text { Distribution }} & t_{9} & t_{10} \\ 95 \% \text { percentile } & 1.83 & 1.81 \\ 97.5 \% \text { percentile } & 2.26 & 2.23\end{array}\right]$

  comment

• 4.I.3H

  Statistics

  Part IB, 2002

  From each of 100 concrete mixes six sample blocks were taken and subjected to strength tests, the number out of the six blocks failing the test being recorded in the following table:

  $$\begin{array}{lrrrrrrr} \text { No. } x \text { failing strength tests } & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \text { No. of mixes with } x \text { failures } & 53 & 32 & 12 & 2 & 1 & 0 & 0 \end{array}$$

  On the assumption that the probability of failure is the same for each block, obtain an unbiased estimate of this probability and explain how to find a $95 \%$ confidence interval for it.

  comment

• 4.II.12H

  Statistics

  Part IB, 2002

  Explain what is meant by a prior distribution, a posterior distribution, and a Bayes estimator. Relate the Bayes estimator to the posterior distribution for both quadratic and absolute error loss functions.

  Suppose $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables from a distribution uniform on $(\theta-1, \theta+1)$, and that the prior for $\theta$ is uniform on $(20,50)$.

  Calculate the posterior distribution for $\theta$, given $\mathbf{x}=\left(x_{1}, \ldots, x_{n}\right)$, and find the point estimate for $\theta$ under both quadratic and absolute error loss function.

  comment

• $1 . \mathrm{I} . 3 \mathrm{H} \quad$

  Statistics

  Part IB, 2003

  Derive the least squares estimators $\hat{\alpha}$ and $\hat{\beta}$ for the coefficients of the simple linear regression model

  $$Y_{i}=\alpha+\beta\left(x_{i}-\bar{x}\right)+\varepsilon_{i}, \quad i=1, \ldots, n,$$

  where $x_{1}, \ldots, x_{n}$ are given constants, $\bar{x}=n^{-1} \sum_{i=1}^{n} x_{i}$, and $\varepsilon_{i}$ are independent with $\mathrm{E} \varepsilon_{i}=0, \operatorname{Var} \varepsilon_{i}=\sigma^{2}, i=1, \ldots, n$.

  A manufacturer of optical equipment has the following data on the unit cost (in pounds) of certain custom-made lenses and the number of units made in each order:

  \begin{tabular}{l|ccccc} No. of units, $x_{i}$ & 1 & 3 & 5 & 10 & 12 \ \hline Cost per unit, $y_{i}$ & 58 & 55 & 40 & 37 & 22 \end{tabular}

  Assuming that the conditions underlying simple linear regression analysis are met, estimate the regression coefficients and use the estimated regression equation to predict the unit cost in an order for 8 of these lenses.

  [Hint: for the data above, $S_{x y}=\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right) y_{i}=-257.4$.]

  comment

• 1.II.12H

  Statistics

  Part IB, 2003

  Suppose that six observations $X_{1}, \ldots, X_{6}$ are selected at random from a normal distribution for which both the mean $\mu_{X}$ and the variance $\sigma_{X}^{2}$ are unknown, and it is found that $S_{X X}=\sum_{i=1}^{6}\left(x_{i}-\bar{x}\right)^{2}=30$, where $\bar{x}=\frac{1}{6} \sum_{i=1}^{6} x_{i}$. Suppose also that 21 observations $Y_{1}, \ldots, Y_{21}$ are selected at random from another normal distribution for which both the mean $\mu_{Y}$ and the variance $\sigma_{Y}^{2}$ are unknown, and it is found that $S_{Y Y}=40$. Derive carefully the likelihood ratio test of the hypothesis $H_{0}: \sigma_{X}^{2}=\sigma_{Y}^{2}$ against $H_{1}: \sigma_{X}^{2}>\sigma_{Y}^{2}$ and apply it to the data above at the $0.05$ level.

  

  comment

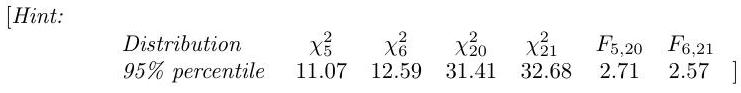
• 2.I.3H

  Statistics

  Part IB, 2003

  Let $X_{1}, \ldots, X_{n}$ be a random sample from the $N\left(\theta, \sigma^{2}\right)$ distribution, and suppose that the prior distribution for $\theta$ is $N\left(\mu, \tau^{2}\right)$, where $\sigma^{2}, \mu, \tau^{2}$ are known. Determine the posterior distribution for $\theta$, given $X_{1}, \ldots, X_{n}$, and the best point estimate of $\theta$ under both quadratic and absolute error loss.

  comment

• 2.II.12H

  Statistics

  Part IB, 2003

  An examination was given to 500 high-school students in each of two large cities, and their grades were recorded as low, medium, or high. The results are given in the table below.

  \begin{tabular}{l|ccc} & Low & Medium & High \ \hline City A & 103 & 145 & 252 \ City B & 140 & 136 & 224 \end{tabular}

  Derive carefully the test of homogeneity and test the hypothesis that the distributions of scores among students in the two cities are the same.

  

  comment

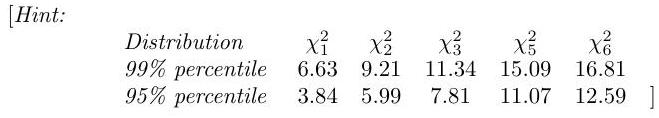
• 4.I.3H

  Statistics

  Part IB, 2003

  The following table contains a distribution obtained in 320 tosses of 6 coins and the corresponding expected frequencies calculated with the formula for the binomial distribution for $p=0.5$ and $n=6$.

  \begin{tabular}{l|rrrrrrr} No. heads & 0 & 1 & 2 & 3 & 4 & 5 & 6 \ \hline Observed frequencies & 3 & 21 & 85 & 110 & 62 & 32 & 7 \ Expected frequencies & 5 & 30 & 75 & 100 & 75 & 30 & 5 \end{tabular}

  Conduct a goodness-of-fit test at the $0.05$ level for the null hypothesis that the coins are all fair.

  [Hint:

  $\left.\begin{array}{lcccc}\text { Distribution } & \chi_{5}^{2} & \chi_{6}^{2} & \chi_{7}^{2} \\ 95 \% \text { percentile } & 11.07 & 12.59 & 14.07 & \end{array}\right]$

  comment

• 4.II.12H $\quad$

  Statistics

  Part IB, 2003

  State and prove the Rao-Blackwell theorem.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent random variables uniformly distributed over $(\theta, 3 \theta)$. Find a two-dimensional sufficient statistic $T(X)$ for $\theta$. Show that an unbiased estimator of $\theta$ is $\hat{\theta}=X_{1} / 2$.

  Find an unbiased estimator of $\theta$ which is a function of $T(X)$ and whose mean square error is no more than that of $\hat{\theta}$.

  comment

• 1.I.10H

  Statistics

  Part IB, 2004

  Use the generalized likelihood-ratio test to derive Student's $t$-test for the equality of the means of two populations. You should explain carefully the assumptions underlying the test.

  comment

• 1.II.21H

  Statistics

  Part IB, 2004

  State and prove the Rao-Blackwell Theorem.

  Suppose that $X_{1}, X_{2}, \ldots, X_{n}$ are independent, identically-distributed random variables with distribution

  $$P\left(X_{1}=r\right)=p^{r-1}(1-p), \quad r=1,2, \ldots$$

  where $p, 0<p<1$, is an unknown parameter. Determine a one-dimensional sufficient statistic, $T$, for $p$.

  By first finding a simple unbiased estimate for $p$, or otherwise, determine an unbiased estimate for $p$ which is a function of $T$.

  comment

• 2.I.10H

  Statistics

  Part IB, 2004

  A study of 60 men and 90 women classified each individual according to eye colour to produce the figures below.

  \begin{tabular}{|c|c|c|c|} \cline { 2 - 4 } \multicolumn{1}{c|}{} & Blue & Brown & Green \ \hline Men & 20 & 20 & 20 \ \hline Women & 20 & 50 & 20 \ \hline \end{tabular}

  Explain how you would analyse these results. You should indicate carefully any underlying assumptions that you are making.

  A further study took 150 individuals and classified them both by eye colour and by whether they were left or right handed to produce the following table.

  \begin{tabular}{|c|c|c|c|} \cline { 2 - 4 } \multicolumn{1}{c|}{} & Blue & Brown & Green \ \hline Left Handed & 20 & 20 & 20 \ \hline Right Handed & 20 & 50 & 20 \ \hline \end{tabular}

  How would your analysis change? You should again set out your underlying assumptions carefully.

  [You may wish to note the following percentiles of the $\chi^{2}$ distribution.

  $\left.\begin{array}{ccccccc} & \chi_{1}^{2} & \chi_{2}^{2} & \chi_{3}^{2} & \chi_{4}^{2} & \chi_{5}^{2} & \chi_{6}^{2} \\ 95 \% \text { percentile } & 3.84 & 5.99 & 7.81 & 9.49 & 11.07 & 12.59 \\ 99 \% \text { percentile } & 6.64 & 9.21 & 11.34 & 13.28 & 15.09 & 16.81\end{array}\right]$

  comment

• 2.II.21H

  Statistics

  Part IB, 2004

  Defining carefully the terminology that you use, state and prove the NeymanPearson Lemma.

  Let $X$ be a single observation from the distribution with density function

  $$f(x \mid \theta)=\frac{1}{2} e^{-|x-\theta|}, \quad-\infty<x<\infty$$

  for an unknown real parameter $\theta$. Find the best test of size $\alpha, 0<\alpha<1$, of the hypothesis $H_{0}: \theta=\theta_{0}$ against $H_{1}: \theta=\theta_{1}$, where $\theta_{1}>\theta_{0}$.

  When $\alpha=0.05$, for which values of $\theta_{0}$ and $\theta_{1}$ will the power of the best test be at least $0.95$ ?

  comment

• 4.I $9 \mathrm{H} \quad$

  Statistics

  Part IB, 2004

  Suppose that $Y_{1}, \ldots, Y_{n}$ are independent random variables, with $Y_{i}$ having the normal distribution with mean $\beta x_{i}$ and variance $\sigma^{2}$; here $\beta, \sigma^{2}$ are unknown and $x_{1}, \ldots, x_{n}$ are known constants.

  Derive the least-squares estimate of $\beta$.

  Explain carefully how to test the hypothesis $H_{0}: \beta=0$ against $H_{1}: \beta \neq 0$.

  comment

• 4.II.19H

  Statistics

  Part IB, 2004

  It is required to estimate the unknown parameter $\theta$ after observing $X$, a single random variable with probability density function $f(x \mid \theta)$; the parameter $\theta$ has the prior distribution with density $\pi(\theta)$ and the loss function is $L(\theta, a)$. Show that the optimal Bayesian point estimate minimizes the posterior expected loss.

  Suppose now that $f(x \mid \theta)=\theta e^{-\theta x}, x>0$ and $\pi(\theta)=\mu e^{-\mu \theta}, \theta>0$, where $\mu>0$ is known. Determine the posterior distribution of $\theta$ given $X$.

  Determine the optimal Bayesian point estimate of $\theta$ in the cases when

  (i) $L(\theta, a)=(\theta-a)^{2}$, and

  (ii) $L(\theta, a)=|(\theta-a) / \theta|$.

  comment

• $1 . \mathrm{I} . 7 \mathrm{D} \quad$

  Statistics

  Part IB, 2005

  The fast-food chain McGonagles have three sizes of their takeaway haggis, Large, Jumbo and Soopersize. A survey of 300 randomly selected customers at one branch choose 92 Large, 89 Jumbo and 119 Soopersize haggises.

  Is there sufficient evidence to reject the hypothesis that all three sizes are equally popular? Explain your answer carefully.

  $$\left[\begin{array}{ccccccccc} \text { Distribution } & t_{1} & t_{2} & t_{3} & \chi_{1}^{2} & \chi_{2}^{2} & \chi_{3}^{2} & F_{1,2} & F_{2,3} \\ \text { 95\% percentile } & 6 \cdot 31 & 2.92 & 2 \cdot 35 & 3.84 & 5.99 & 7 \cdot 82 & 18 \cdot 51 & 9.55 \end{array}\right]$$

  comment

• 1.II.18D

  Statistics

  Part IB, 2005

  In the context of hypothesis testing define the following terms: (i) simple hypothesis; (ii) critical region; (iii) size; (iv) power; and (v) type II error probability.

  State, without proof, the Neyman-Pearson lemma.

  Let $X$ be a single observation from a probability density function $f$. It is desired to test the hypothesis

  $$H_{0}: f=f_{0} \quad \text { against } \quad H_{1}: f=f_{1},$$

  with $f_{0}(x)=\frac{1}{2}|x| e^{-x^{2} / 2}$ and $f_{1}(x)=\Phi^{\prime}(x),-\infty<x<\infty$, where $\Phi(x)$ is the distribution function of the standard normal, $N(0,1)$.

  Determine the best test of size $\alpha$, where $0<\alpha<1$, and express its power in terms of $\Phi$ and $\alpha$.

  Find the size of the test that minimizes the sum of the error probabilities. Explain your reasoning carefully.

  comment

• 2.II.19D

  Statistics

  Part IB, 2005

  Let $X_{1}, \ldots, X_{n}$ be a random sample from a probability density function $f(x \mid \theta)$, where $\theta$ is an unknown real-valued parameter which is assumed to have a prior density $\pi(\theta)$. Determine the optimal Bayes point estimate $a\left(X_{1}, \ldots, X_{n}\right)$ of $\theta$, in terms of the posterior distribution of $\theta$ given $X_{1}, \ldots, X_{n}$, when the loss function is

  $$L(\theta, a)= \begin{cases}\gamma(\theta-a) & \text { when } \theta \geqslant a \\ \delta(a-\theta) & \text { when } \theta \leqslant a\end{cases}$$

  where $\gamma$ and $\delta$ are given positive constants.

  Calculate the estimate explicitly in the case when $f(x \mid \theta)$ is the density of the uniform distribution on $(0, \theta)$ and $\pi(\theta)=e^{-\theta} \theta^{n} / n !, \theta>0$.

  comment

• 3.I.8D

  Statistics

  Part IB, 2005

  Let $X_{1}, \ldots, X_{n}$ be a random sample from a normal distribution with mean $\mu$ and variance $\sigma^{2}$, where $\mu$ and $\sigma^{2}$ are unknown. Derive the form of the size- $\alpha$ generalized likelihood-ratio test of the hypothesis $H_{0}: \mu=\mu_{0}$ against $H_{1}: \mu \neq \mu_{0}$, and show that it is equivalent to the standard $t$-test of size $\alpha$.

  [You should state, but need not derive, the distribution of the test statistic.]

  comment

• 4.II.19D

  Statistics

  Part IB, 2005

  Let $Y_{1}, \ldots, Y_{n}$ be observations satisfying

  $$Y_{i}=\beta x_{i}+\epsilon_{i}, \quad 1 \leqslant i \leqslant n$$

  where $\epsilon_{1}, \ldots, \epsilon_{n}$ are independent random variables each with the $N\left(0, \sigma^{2}\right)$ distribution. Here $x_{1}, \ldots, x_{n}$ are known but $\beta$ and $\sigma^{2}$ are unknown.

  (i) Determine the maximum-likelihood estimates $\left(\widehat{\beta}, \widehat{\sigma}^{2}\right)$ of $\left(\beta, \sigma^{2}\right)$.

  (ii) Find the distribution of $\widehat{\beta}$.

  (iii) By showing that $Y_{i}-\widehat{\beta} x_{i}$ and $\widehat{\beta}$ are independent, or otherwise, determine the joint distribution of $\widehat{\beta}$ and $\widehat{\sigma}^{2}$.

  (iv) Explain carefully how you would test the hypothesis $H_{0}: \beta=\beta_{0}$ against $H_{1}: \beta \neq \beta_{0}$.

  comment

• $1 . \mathrm{I} . 7 \mathrm{C} \quad$

  Statistics

  Part IB, 2006

  A random sample $X_{1}, \ldots, X_{n}$ is taken from a normal distribution having unknown mean $\theta$ and variance 1. Find the maximum likelihood estimate $\hat{\theta}_{M}$ for $\theta$ based on $X_{1}, \ldots, X_{n}$.

  Suppose that we now take a Bayesian point of view and regard $\theta$ itself as a normal random variable of known mean $\mu$ and variance $\tau^{-1}$. Find the Bayes' estimate $\hat{\theta}_{B}$ for $\theta$ based on $X_{1}, \ldots, X_{n}$, corresponding to the quadratic loss function $(\theta-a)^{2}$.

  comment

• 1.II.18C

  Statistics

  Part IB, 2006

  Let $X$ be a random variable whose distribution depends on an unknown parameter $\theta$. Explain what is meant by a sufficient statistic $T(X)$ for $\theta$.

  In the case where $X$ is discrete, with probability mass function $f(x \mid \theta)$, explain, with justification, how a sufficient statistic may be found.

  Assume now that $X=\left(X_{1}, \ldots, X_{n}\right)$, where $X_{1}, \ldots, X_{n}$ are independent nonnegative random variables with common density function

  $$f(x \mid \theta)= \begin{cases}\lambda e^{-\lambda(x-\theta)} & \text { if } x \geqslant \theta \\ 0 & \text { otherwise }\end{cases}$$

  Here $\theta \geq 0$ is unknown and $\lambda$ is a known positive parameter. Find a sufficient statistic for $\theta$ and hence obtain an unbiased estimator $\hat{\theta}$ for $\theta$ of variance $(n \lambda)^{-2}$.

  [You may use without proof the following facts: for independent exponential random variables $X$ and $Y$, having parameters $\lambda$ and $\mu$ respectively, $X$ has mean $\lambda^{-1}$ and variance $\lambda^{-2}$ and $\min \{X, Y\}$ has exponential distribution of parameter $\lambda+\mu$.]

  comment

• 2.II.19C

  Statistics

  Part IB, 2006

  Suppose that $X_{1}, \ldots, X_{n}$ are independent normal random variables of unknown mean $\theta$ and variance 1 . It is desired to test the hypothesis $H_{0}: \theta \leq 0$ against the alternative $H_{1}: \theta>0$. Show that there is a uniformly most powerful test of size $\alpha=1 / 20$ and identify a critical region for such a test in the case $n=9$. If you appeal to any theoretical result from the course you should also prove it.

  [The 95th percentile of the standard normal distribution is 1.65.]

  comment

• 3.I.8C

  Statistics

  Part IB, 2006

  One hundred children were asked whether they preferred crisps, fruit or chocolate. Of the boys, 12 stated a preference for crisps, 11 for fruit, and 17 for chocolate. Of the girls, 13 stated a preference for crisps, 14 for fruit, and 33 for chocolate. Answer each of the following questions by carrying out an appropriate statistical test.

  (a) Are the data consistent with the hypothesis that girls find all three types of snack equally attractive?

  (b) Are the data consistent with the hypothesis that boys and girls show the same distribution of preferences?

  comment

• 4.II.19C

  Statistics

  Part IB, 2006

  Two series of experiments are performed, the first resulting in observations $X_{1}, \ldots, X_{m}$, the second resulting in observations $Y_{1}, \ldots, Y_{n}$. We assume that all observations are independent and normally distributed, with unknown means $\mu_{X}$ in the first series and $\mu_{Y}$ in the second series. We assume further that the variances of the observations are unknown but are all equal.

  Write down the distributions of the sample mean $\bar{X}=m^{-1} \sum_{i=1}^{m} X_{i}$ and sum of squares $S_{X X}=\sum_{i=1}^{m}\left(X_{i}-\bar{X}\right)^{2}$.

  Hence obtain a statistic $T(X, Y)$ to test the hypothesis $H_{0}: \mu_{X}=\mu_{Y}$ against $H_{1}: \mu_{X}>\mu_{Y}$ and derive its distribution under $H_{0}$. Explain how you would carry out a test of size $\alpha=1 / 100$.

  comment

• 1.I.7C

  Statistics

  Part IB, 2007

  Let $X_{1}, \ldots, X_{n}$ be independent, identically distributed random variables from the $N\left(\mu, \sigma^{2}\right)$ distribution where $\mu$ and $\sigma^{2}$ are unknown. Use the generalized likelihood-ratio test to derive the form of a test of the hypothesis $H_{0}: \mu=\mu_{0}$ against $H_{1}: \mu \neq \mu_{0}$.

  Explain carefully how the test should be implemented.

  comment

• 1.II.18C

  Statistics

  Part IB, 2007

  Let $X_{1}, \ldots, X_{n}$ be independent, identically distributed random variables with

  $$\mathbb{P}\left(X_{i}=1\right)=\theta=1-\mathbb{P}\left(X_{i}=0\right)$$

  where $\theta$ is an unknown parameter, $0<\theta<1$, and $n \geqslant 2$. It is desired to estimate the quantity $\phi=\theta(1-\theta)=n \operatorname{Var}\left(\left(X_{1}+\cdots+X_{n}\right) / n\right)$.

  (i) Find the maximum-likelihood estimate, $\hat{\phi}$, of $\phi$.

  (ii) Show that $\hat{\phi}_{1}=X_{1}\left(1-X_{2}\right)$ is an unbiased estimate of $\phi$ and hence, or otherwise, obtain an unbiased estimate of $\phi$ which has smaller variance than $\hat{\phi}_{1}$ and which is a function of $\hat{\phi}$.

  (iii) Now suppose that a Bayesian approach is adopted and that the prior distribution for $\theta, \pi(\theta)$, is taken to be the uniform distribution on $(0,1)$. Compute the Bayes point estimate of $\phi$ when the loss function is $L(\phi, a)=(\phi-a)^{2}$.

  [You may use that fact that when $r, s$ are non-negative integers,

  $$\left.\int_{0}^{1} x^{r}(1-x)^{s} d x=r ! s ! /(r+s+1) !\right]$$

  comment

• 2.II.19C

  Statistics

  Part IB, 2007

  State and prove the Neyman-Pearson lemma.

  Suppose that $X$ is a random variable drawn from the probability density function

  $$f(x \mid \theta)=\frac{1}{2}|x|^{\theta-1} e^{-|x|} / \Gamma(\theta), \quad-\infty<x<\infty$$

  where $\Gamma(\theta)=\int_{0}^{\infty} y^{\theta-1} e^{-y} d y$ and $\theta \geqslant 1$ is unknown. Find the most powerful test of size $\alpha$, $0<\alpha<1$, of the hypothesis $H_{0}: \theta=1$ against the alternative $H_{1}: \theta=2$. Express the power of the test as a function of $\alpha$.

  Is your test uniformly most powerful for testing $H_{0}: \theta=1$ against $H_{1}: \theta>1 ?$ Explain your answer carefully.

  comment

• 3.I.8C

  Statistics

  Part IB, 2007

  Light bulbs are sold in packets of 3 but some of the bulbs are defective. A sample of 256 packets yields the following figures for the number of defectives in a packet:

  \begin{tabular}{l|cccc} No. of defectives & 0 & 1 & 2 & 3 \ \hline No. of packets & 116 & 94 & 40 & 6 \end{tabular}

  Test the hypothesis that each bulb has a constant (but unknown) probability $\theta$ of being defective independently of all other bulbs.

  [Hint: You may wish to use some of the following percentage points:

  $\left.\begin{array}{c|ccccccccc}\text { Distribution } & \chi_{1}^{2} & \chi_{2}^{2} & \chi_{3}^{2} & \chi_{4}^{2} & t_{1} & t_{2} & t_{3} & t_{4} \\ \hline 90 \% \text { percentile } & 2 \cdot 71 & 4 \cdot 61 & 6.25 & 7 \cdot 78 & 3 \cdot 08 & 1.89 & 1 \cdot 64 & 1.53 \\ 95 \% \text { percentile } & 3.84 & 5.99 & 7 \cdot 81 & 9 \cdot 49 & 6 \cdot 31 & 2.92 & 2 \cdot 35 & 2 \cdot 13\end{array}\right]$

  comment

• 4.II.19C

  Statistics

  Part IB, 2007

  Consider the linear regression model

  $$Y_{i}=\alpha+\beta x_{i}+\epsilon_{i}, \quad 1 \leqslant i \leqslant n$$

  where $\epsilon_{1}, \ldots, \epsilon_{n}$ are independent, identically distributed $N\left(0, \sigma^{2}\right), x_{1}, \ldots, x_{n}$ are known real numbers with $\sum_{i=1}^{n} x_{i}=0$ and $\alpha, \beta$ and $\sigma^{2}$ are unknown.

  (i) Find the least-squares estimates $\widehat{\alpha}$and $\widehat{\beta}$ of $\alpha$ and $\beta$, respectively, and explain why in this case they are the same as the maximum-likelihood estimates.

  (ii) Determine the maximum-likelihood estimate $\widehat{\sigma}^{2}$ of $\sigma^{2}$ and find a multiple of it which is an unbiased estimate of $\sigma^{2}$.

  (iii) Determine the joint distribution of $\widehat{\alpha}, \widehat{\beta}$ and $\widehat{\sigma}^{2}$.

  (iv) Explain carefully how you would test the hypothesis $H_{0}: \alpha=\alpha_{0}$ against the alternative $H_{1}: \alpha \neq \alpha_{0}$.

  comment

• $1 . \mathrm{I} . 7 \mathrm{H} \quad$

  Statistics

  Part IB, 2008

  A Bayesian statistician observes a random sample $X_{1}, \ldots, X_{n}$ drawn from a $N\left(\mu, \tau^{-1}\right)$ distribution. He has a prior density for the unknown parameters $\mu, \tau$ of the form

  $$\pi_{0}(\mu, \tau) \propto \tau^{\alpha_{0}-1} \exp \left(-\frac{1}{2} K_{0} \tau\left(\mu-\mu_{0}\right)^{2}-\beta_{0} \tau\right) \sqrt{\tau},$$

  where $\alpha_{0}, \beta_{0}, \mu_{0}$ and $K_{0}$ are constants which he chooses. Show that after observing $X_{1}, \ldots, X_{n}$ his posterior density $\pi_{n}(\mu, \tau)$ is again of the form

  $$\pi_{n}(\mu, \tau) \propto \tau^{\alpha_{n}-1} \exp \left(-\frac{1}{2} K_{n} \tau\left(\mu-\mu_{n}\right)^{2}-\beta_{n} \tau\right) \sqrt{\tau}$$

  where you should find explicitly the form of $\alpha_{n}, \beta_{n}, \mu_{n}$ and $K_{n}$.

  comment

• 1.II.18H

  Statistics

  Part IB, 2008

  Suppose that $X_{1}, \ldots, X_{n}$ is a sample of size $n$ with common $N\left(\mu_{X}, 1\right)$ distribution, and $Y_{1}, \ldots, Y_{n}$ is an independent sample of size $n$ from a $N\left(\mu_{Y}, 1\right)$ distribution.

  (i) Find (with careful justification) the form of the size- $\alpha$ likelihood-ratio test of the null hypothesis $H_{0}: \mu_{Y}=0$ against alternative $H_{1}:\left(\mu_{X}, \mu_{Y}\right)$ unrestricted.

  (ii) Find the form of the size- $\alpha$ likelihood-ratio test of the hypothesis

  $$H_{0}: \mu_{X} \geqslant A, \mu_{Y}=0$$

  against $H_{1}:\left(\mu_{X}, \mu_{Y}\right)$ unrestricted, where $A$ is a given constant.

  Compare the critical regions you obtain in (i) and (ii) and comment briefly.

  comment

• 2.II.19H

  Statistics

  Part IB, 2008

  Suppose that the joint distribution of random variables $X, Y$ taking values in $\mathbb{Z}^{+}=\{0,1,2, \ldots\}$ is given by the joint probability generating function

  $$\varphi(s, t) \equiv E\left[s^{X} t^{Y}\right]=\frac{1-\alpha-\beta}{1-\alpha s-\beta t}$$

  where the unknown parameters $\alpha$ and $\beta$ are positive, and satisfy the inequality $\alpha+\beta<1$. Find $E(X)$. Prove that the probability mass function of $(X, Y)$ is

  $$f(x, y \mid \alpha, \beta)=(1-\alpha-\beta)\left(\begin{array}{c} x+y \\ x \end{array}\right) \alpha^{x} \beta^{y} \quad\left(x, y \in \mathbb{Z}^{+}\right)$$

  and prove that the maximum-likelihood estimators of $\alpha$ and $\beta$ based on a sample of size $n$ drawn from the distribution are

  $$\hat{\alpha}=\frac{\bar{X}}{1+\bar{X}+\bar{Y}}, \quad \hat{\beta}=\frac{\bar{Y}}{1+\bar{X}+\bar{Y}},$$

  where $\bar{X}$ (respectively, $\bar{Y}$ ) is the sample mean of $X_{1}, \ldots, X_{n}$ (respectively, $Y_{1}, \ldots, Y_{n}$ ).

  By considering $\hat{\alpha}+\hat{\beta}$ or otherwise, prove that the maximum-likelihood estimator is biased. Stating clearly any results to which you appeal, prove that as $n \rightarrow \infty, \hat{\alpha} \rightarrow \alpha$, making clear the sense in which this convergence happens.

  comment

• $3 . \mathrm{I} . 8 \mathrm{H} \quad$

  Statistics

  Part IB, 2008

  If $X_{1}, \ldots, X_{n}$ is a sample from a density $f(\cdot \mid \theta)$ with $\theta$ unknown, what is a $95 \%$ confidence set for $\theta$ ?

  In the case where the $X_{i}$ are independent $N\left(\mu, \sigma^{2}\right)$ random variables with $\sigma^{2}$ known, $\mu$ unknown, find (in terms of $\sigma^{2}$ ) how large the size $n$ of the sample must be in order for there to exist a $95 \%$ confidence interval for $\mu$ of length no more than some given $\varepsilon>0$.

  [Hint: If $Z \sim N(0,1)$ then $P(Z>1.960)=0.025 .]$

  comment

• 4.II.19H

  Statistics

  Part IB, 2008

  (i) Consider the linear model

  $$Y_{i}=\alpha+\beta x_{i}+\varepsilon_{i}$$

  where observations $Y_{i}, i=1, \ldots, n$, depend on known explanatory variables $x_{i}$, $i=1, \ldots, n$, and independent $N\left(0, \sigma^{2}\right)$ random variables $\varepsilon_{i}, i=1, \ldots, n$.

  Derive the maximum-likelihood estimators of $\alpha, \beta$ and $\sigma^{2}$.

  Stating clearly any results you require about the distribution of the maximum-likelihood estimators of $\alpha, \beta$ and $\sigma^{2}$, explain how to construct a test of the hypothesis that $\alpha=0$ against an unrestricted alternative.

  (ii) A simple ballistic theory predicts that the range of a gun fired at angle of elevation $\theta$ should be given by the formula

  $$Y=\frac{V^{2}}{g} \sin 2 \theta$$

  where $V$ is the muzzle velocity, and $g$ is the gravitational acceleration. Shells are fired at 9 different elevations, and the ranges observed are as follows:

  $\begin{array}{cccccccccc}\theta \text { (degrees) } & 5 & 15 & 25 & 35 & 45 & 55 & 65 & 75 & 85 \\ \sin 2 \theta & 0.1736 & 0.5 & 0.7660 & 0.9397 & 1 & 0.9397 & 0.7660 & 0.5 & 0.1736 \\ Y(\mathrm{~m}) & 4322 & 11898 & 17485 & 20664 & 21296 & 19491 & 15572 & 10027 & 3458\end{array}$

  The model

  $$Y_{i}=\alpha+\beta \sin 2 \theta_{i}+\varepsilon_{i}$$

  is proposed. Using the theory of part (i) above, find expressions for the maximumlikelihood estimators of $\alpha$ and $\beta$.

  The $t$-test of the null hypothesis that $\alpha=0$ against an unrestricted alternative does not reject the null hypothesis. Would you be willing to accept the model $(*)$ ? Briefly explain your answer.

  [You may need the following summary statistics of the data. If $x_{i}=\sin 2 \theta_{i}$, then $\bar{x} \equiv n^{-1} \sum x_{i}=0.63986, \bar{Y}=13802, S_{x x} \equiv \sum\left(x_{i}-\bar{x}\right)^{2}=0.81517, S_{x y}=\sum Y_{i}\left(x_{i}-\bar{x}\right)=$ 17186. ]

  comment

• Paper 1, Section I, $\mathbf{7 H} \quad$

  Statistics

  Part IB, 2009

  What does it mean to say that an estimator $\hat{\theta}$ of a parameter $\theta$ is unbiased?

  An $n$-vector $Y$ of observations is believed to be explained by the model

  $$Y=X \beta+\varepsilon$$

  where $X$ is a known $n \times p$ matrix, $\beta$ is an unknown $p$-vector of parameters, $p<n$, and $\varepsilon$ is an $n$-vector of independent $N\left(0, \sigma^{2}\right)$ random variables. Find the maximum-likelihood estimator $\hat{\beta}$ of $\beta$, and show that it is unbiased.

  comment

• Paper 3, Section $\mathbf{I}$, H

  Statistics

  Part IB, 2009

  In a demographic study, researchers gather data on the gender of children in families with more than two children. For each of the four possible outcomes $G G, G B, B G, B B$ of the first two children in the family, they find 50 families which started with that pair, and record the gender of the third child of the family. This produces the following table of counts:

  First two children Third child $B$ Third child $G$

  $\begin{array}{ccc}G G & 16 & 34 \\ G B & 28 & 22 \\ B G & 25 & 25 \\ B B & 31 & 19\end{array}$

  In view of this, is the hypothesis that the gender of the third child is independent of the genders of the first two children rejected at the $5 \%$ level?

  [Hint: the $95 \%$ point of a $\chi_{3}^{2}$ distribution is $7.8147$, and the $95 \%$ point of a $\chi_{4}^{2}$ distribution is $9.4877 .]$

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2009

  What is the critical region $C$ of a test of the null hypothesis $H_{0}: \theta \in \Theta_{0}$ against the alternative $H_{1}: \theta \in \Theta_{1}$ ? What is the size of a test with critical region $C ?$ What is the power function of a test with critical region $C$ ?

  State and prove the Neyman-Pearson Lemma.

  If $X_{1}, \ldots, X_{n}$ are independent with $\operatorname{common} \operatorname{Exp}(\lambda)$ distribution, and $0<\lambda_{0}<\lambda_{1}$, find the form of the most powerful size- $\alpha$ test of $H_{0}: \lambda=\lambda_{0}$ against $H_{1}: \lambda=\lambda_{1}$. Find the power function as explicitly as you can, and prove that it is increasing in $\lambda$. Deduce that the test you have constructed is a size- $\alpha$ test of $H_{0}: \lambda \leqslant \lambda_{0}$ against $H_{1}: \lambda=\lambda_{1}$.

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2009

  What is a sufficient statistic? State the factorization criterion for a statistic to be sufficient.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent random variables uniformly distributed over $[a, b]$, where the parameters $a<b$ are not known, and $n \geqslant 2$. Find a sufficient statistic for the parameter $\theta \equiv(a, b)$ based on the sample $X_{1}, \ldots, X_{n}$. Based on your sufficient statistic, derive an unbiased estimator of $\theta$.

  comment

• Paper 2, Section II, H

  Statistics

  Part IB, 2009

  What does it mean to say that the random $d$-vector $X$ has a multivariate normal distribution with mean $\mu$ and covariance matrix $\Sigma$ ?

  Suppose that $X \sim N_{d}\left(0, \sigma^{2} I_{d}\right)$, and that for each $j=1, \ldots, J, A_{j}$ is a $d_{j} \times d$ matrix. Suppose further that

  $$A_{j} A_{i}^{T}=0$$

  for $j \neq i$. Prove that the random vectors $Y_{j} \equiv A_{j} X$ are independent, and that $Y \equiv\left(Y_{1}^{T}, \ldots, Y_{J}^{T}\right)^{T}$ has a multivariate normal distribution.

  [Hint: Random vectors are independent if their joint $M G F$ is the product of their individual MGFs.]

  If $Z_{1}, \ldots, Z_{n}$ is an independent sample from a univariate $N\left(\mu, \sigma^{2}\right)$ distribution, prove that the sample variance $S_{Z Z} \equiv(n-1)^{-1} \sum_{i=1}^{n}\left(Z_{i}-\bar{Z}\right)^{2}$ and the sample mean $\bar{Z} \equiv$ $n^{-1} \sum_{i=1}^{n} Z_{i}$ are independent.

  comment

• Paper 1, Section I, E

  Statistics

  Part IB, 2010

  Suppose $X_{1}, \ldots, X_{n}$ are independent $N\left(0, \sigma^{2}\right)$ random variables, where $\sigma^{2}$ is an unknown parameter. Explain carefully how to construct the uniformly most powerful test of size $\alpha$ for the hypothesis $H_{0}: \sigma^{2}=1$ versus the alternative $H_{1}: \sigma^{2}>1$.

  comment

• Paper 2, Section I, E

  Statistics

  Part IB, 2010

  A washing powder manufacturer wants to determine the effectiveness of a television advertisement. Before the advertisement is shown, a pollster asks 100 randomly chosen people which of the three most popular washing powders, labelled $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$, they prefer. After the advertisement is shown, another 100 randomly chosen people (not the same as before) are asked the same question. The results are summarized below.

  \begin{tabular}{c|ccc} & $\mathrm{A}$ & $\mathrm{B}$ & $\mathrm{C}$ \ \hline before & 36 & 47 & 17 \ after & 44 & 33 & 23 \end{tabular}

  Derive and carry out an appropriate test at the $5 \%$ significance level of the hypothesis that the advertisement has had no effect on people's preferences.

  [You may find the following table helpful:

  $\left.\begin{array}{c|cccccc} & \chi_{1}^{2} & \chi_{2}^{2} & \chi_{3}^{2} & \chi_{4}^{2} & \chi_{5}^{2} & \chi_{6}^{2} \\ \hline 95 \text { percentile } & 3.84 & 5.99 & 7.82 & 9.49 & 11.07 & 12.59\end{array} \cdot\right]$

  comment

• Paper 1, Section II, E

  Statistics

  Part IB, 2010

  Consider the the linear regression model

  $$Y_{i}=\beta x_{i}+\epsilon_{i},$$

  where the numbers $x_{1}, \ldots, x_{n}$ are known, the independent random variables $\epsilon_{1}, \ldots, \epsilon_{n}$ have the $N\left(0, \sigma^{2}\right)$ distribution, and the parameters $\beta$ and $\sigma^{2}$ are unknown. Find the maximum likelihood estimator for $\beta$.

  State and prove the Gauss-Markov theorem in the context of this model.

  Write down the distribution of an arbitrary linear estimator for $\beta$. Hence show that there exists a linear, unbiased estimator $\widehat{\beta}$ for $\beta$ such that

  $$\mathbb{E}_{\beta, \sigma^{2}}\left[(\widehat{\beta}-\beta)^{4}\right] \leqslant \mathbb{E}_{\beta, \sigma^{2}}\left[(\widetilde{\beta}-\beta)^{4}\right]$$

  for all linear, unbiased estimators $\widetilde{\beta}$.

  [Hint: If $Z \sim N\left(a, b^{2}\right)$ then $\left.\mathbb{E}\left[(Z-a)^{4}\right]=3 b^{4} .\right]$

  comment

• Paper 3, Section II, E

  Statistics

  Part IB, 2010

  Let $X_{1}, \ldots, X_{n}$ be independent $\operatorname{Exp}(\theta)$ random variables with unknown parameter $\theta$. Find the maximum likelihood estimator $\hat{\theta}$ of $\theta$, and state the distribution of $n / \hat{\theta}$. Show that $\theta / \hat{\theta}$ has the $\Gamma(n, n)$ distribution. Find the $100(1-\alpha) \%$ confidence interval for $\theta$ of the form $[0, C \hat{\theta}]$ for a constant $C>0$ depending on $\alpha$.

  Now, taking a Bayesian point of view, suppose your prior distribution for the parameter $\theta$ is $\Gamma(k, \lambda)$. Show that your Bayesian point estimator $\hat{\theta}_{B}$ of $\theta$ for the loss function $L(\theta, a)=(\theta-a)^{2}$ is given by

  $$\hat{\theta}_{B}=\frac{n+k}{\lambda+\sum_{i} X_{i}} .$$

  Find a constant $C_{B}>0$ depending on $\alpha$ such that the posterior probability that $\theta \leqslant C_{B} \hat{\theta}_{B}$ is equal to $1-\alpha$.

  [The density of the $\Gamma(k, \lambda)$ distribution is $f(x ; k, \lambda)=\lambda^{k} x^{k-1} e^{-\lambda x} / \Gamma(k)$, for $\left.x>0 .\right]$

  comment

• Paper 4, Section II, E

  Statistics

  Part IB, 2010

  Consider a collection $X_{1}, \ldots, X_{n}$ of independent random variables with common density function $f(x ; \theta)$ depending on a real parameter $\theta$. What does it mean to say $T$ is a sufficient statistic for $\theta$ ? Prove that if the joint density of $X_{1}, \ldots, X_{n}$ satisfies the factorisation criterion for a statistic $T$, then $T$ is sufficient for $\theta$.

  Let each $X_{i}$ be uniformly distributed on $[-\sqrt{\theta}, \sqrt{\theta}]$. Find a two-dimensional sufficient statistic $T=\left(T_{1}, T_{2}\right)$. Using the fact that $\hat{\theta}=3 X_{1}^{2}$ is an unbiased estimator of $\theta$, or otherwise, find an unbiased estimator of $\theta$ which is a function of $T$ and has smaller variance than $\hat{\theta}$. Clearly state any results you use.

  comment

• Paper 1, Section I, $\mathbf{7 H} \quad$

  Statistics

  Part IB, 2011

  Consider the experiment of tossing a coin $n$ times. Assume that the tosses are independent and the coin is biased, with unknown probability $p$ of heads and $1-p$ of tails. A total of $X$ heads is observed.

  (i) What is the maximum likelihood estimator $\widehat{p}$ of $p$ ?

  Now suppose that a Bayesian statistician has the $\operatorname{Beta}(M, N)$ prior distribution for $p$.

  (ii) What is the posterior distribution for $p$ ?

  (iii) Assuming the loss function is $L(p, a)=(p-a)^{2}$, show that the statistician's point estimate for $p$ is given by

  $$\frac{M+X}{M+N+n}$$

  [The $\operatorname{Beta}(M, N)$ distribution has density $\frac{\Gamma(M+N)}{\Gamma(M) \Gamma(N)} x^{M-1}(1-x)^{N-1}$ for $0<x<1$ and $\left.\operatorname{mean} \frac{M}{M+N} .\right]$

  comment

• Paper 2, Section I, H

  Statistics

  Part IB, 2011

  Let $X_{1}, \ldots, X_{n}$ be random variables with joint density function $f\left(x_{1}, \ldots, x_{n} ; \theta\right)$, where $\theta$ is an unknown parameter. The null hypothesis $H_{0}: \theta=\theta_{0}$ is to be tested against the alternative hypothesis $H_{1}: \theta=\theta_{1}$.

  (i) Define the following terms: critical region, Type I error, Type II error, size, power.

  (ii) State and prove the Neyman-Pearson lemma.

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2011

  Let $X_{1}, \ldots, X_{n}$ be independent random variables with probability mass function $f(x ; \theta)$, where $\theta$ is an unknown parameter.

  (i) What does it mean to say that $T$ is a sufficient statistic for $\theta$ ? State, but do not prove, the factorisation criterion for sufficiency.

  (ii) State and prove the Rao-Blackwell theorem.

  Now consider the case where $f(x ; \theta)=\frac{1}{x !}(-\log \theta)^{x} \theta$ for non-negative integer $x$ and $0<\theta<1$.

  (iii) Find a one-dimensional sufficient statistic $T$ for $\theta$.

  (iv) Show that $\tilde{\theta}=\mathbb{\prod}_{\left\{X_{1}=0\right\}}$ is an unbiased estimator of $\theta$.

  (v) Find another unbiased estimator $\widehat{\theta}$which is a function of the sufficient statistic $T$ and that has smaller variance than $\tilde{\theta}$. You may use the following fact without proof: $X_{1}+\cdots+X_{n}$ has the Poisson distribution with parameter $-n \log \theta$.

  comment

• Paper 3, Section II, H

  Statistics

  Part IB, 2011

  Consider the general linear model

  $$Y=X \beta+\epsilon$$

  where $X$ is a known $n \times p$ matrix, $\beta$ is an unknown $p \times 1$ vector of parameters, and $\epsilon$ is an $n \times 1$ vector of independent $N\left(0, \sigma^{2}\right)$ random variables with unknown variance $\sigma^{2}$. Assume the $p \times p$ matrix $X^{T} X$ is invertible.

  (i) Derive the least squares estimator $\widehat{\beta}$ of $\beta$.

  (ii) Derive the distribution of $\widehat{\beta}$. Is $\widehat{\beta}$ an unbiased estimator of $\beta$ ?

  (iii) Show that $\frac{1}{\sigma^{2}}\|Y-X \widehat{\beta}\|^{2}$ has the $\chi^{2}$ distribution with $k$ degrees of freedom, where $k$ is to be determined.

  (iv) Let $\tilde{\beta}$ be an unbiased estimator of $\beta$ of the form $\tilde{\beta}=C Y$ for some $p \times n$ matrix $C$. By considering the matrix $\mathbb{E}\left[(\widehat{\beta}-\widetilde{\beta})(\widehat{\beta}-\beta)^{T}\right]$ or otherwise, show that $\widehat{\beta}$ and $\widehat{\beta}-\widetilde{\beta}$ are independent.

  [You may use standard facts about the multivariate normal distribution as well as results from linear algebra, including the fact that $I-X\left(X^{T} X\right)^{-1} X^{T}$ is a projection matrix of rank $n-p$, as long as they are carefully stated.]

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2011

  Consider independent random variables $X_{1}, \ldots, X_{n}$ with the $N\left(\mu_{X}, \sigma_{X}^{2}\right)$ distribution and $Y_{1}, \ldots, Y_{n}$ with the $N\left(\mu_{Y}, \sigma_{Y}^{2}\right)$ distribution, where the means $\mu_{X}, \mu_{Y}$ and variances $\sigma_{X}^{2}, \sigma_{Y}^{2}$ are unknown. Derive the generalised likelihood ratio test of size $\alpha$ of the null hypothesis $H_{0}: \sigma_{X}^{2}=\sigma_{Y}^{2}$ against the alternative $H_{1}: \sigma_{X}^{2} \neq \sigma_{Y}^{2}$. Express the critical region in terms of the statistic $T=\frac{S_{X X}}{S_{X X}+S_{Y Y}}$ and the quantiles of a beta distribution, where

  $$S_{X X}=\sum_{i=1}^{n} X_{i}^{2}-\frac{1}{n}\left(\sum_{i=1}^{n} X_{i}\right)^{2} \text { and } S_{Y Y}=\sum_{i=1}^{n} Y_{i}^{2}-\frac{1}{n}\left(\sum_{i=1}^{n} Y_{i}\right)^{2}$$

  [You may use the following fact: if $U \sim \Gamma(a, \lambda)$ and $V \sim \Gamma(b, \lambda)$ are independent, then $\left.\frac{U}{U+V} \sim \operatorname{Beta}(a, b) .\right]$

  comment

• Paper 1, Section I, H

  Statistics

  Part IB, 2012

  Describe the generalised likelihood ratio test and the type of statistical question for which it is useful.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent and identically distributed random variables with the Gamma $(2, \lambda)$ distribution, having density function $\lambda^{2} x \exp (-\lambda x), x \geqslant 0$. Similarly, $Y_{1}, \ldots, Y_{n}$ are independent and identically distributed with the Gamma $(2, \mu)$ distribution. It is desired to test the hypothesis $H_{0}: \lambda=\mu$ against $H_{1}: \lambda \neq \mu$. Derive the generalised likelihood ratio test and express it in terms of $R=\sum_{i} X_{i} / \sum_{i} Y_{i}$.

  Let $F_{\nu_{1}, \nu_{2}}^{(1-\alpha)}$ denote the value that a random variable having the $F_{\nu_{1}, \nu_{2}}$ distribution exceeds with probability $\alpha$. Explain how to decide the outcome of a size $0.05$ test when $n=5$ by knowing only the value of $R$ and the value $F_{\nu_{1}, \nu_{2}}^{(1-\alpha)}$, for some $\nu_{1}, \nu_{2}$ and $\alpha$, which you should specify.

  [You may use the fact that the $\chi_{k}^{2}$ distribution is equivalent to the $\operatorname{Gamma}(k / 2,1 / 2)$ distribution.]

  comment

• Paper 2, Section I, H

  Statistics

  Part IB, 2012

  Let the sample $x=\left(x_{1}, \ldots, x_{n}\right)$ have likelihood function $f(x ; \theta)$. What does it mean to say $T(x)$ is a sufficient statistic for $\theta$ ?

  Show that if a certain factorization criterion is satisfied then $T$ is sufficient for $\theta$.

  Suppose that $T$ is sufficient for $\theta$ and there exist two samples, $x$ and $y$, for which $T(x) \neq T(y)$ and $f(x ; \theta) / f(y ; \theta)$ does not depend on $\theta$. Let

  $$T_{1}(z)= \begin{cases}T(z) & z \neq y \\ T(x) & z=y\end{cases}$$

  Show that $T_{1}$ is also sufficient for $\theta$.

  Explain why $T$ is not minimally sufficient for $\theta$.

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2012

  From each of 3 populations, $n$ data points are sampled and these are believed to obey

  $$y_{i j}=\alpha_{i}+\beta_{i}\left(x_{i j}-\bar{x}_{i}\right)+\epsilon_{i j}, \quad j \in\{1, \ldots, n\}, i \in\{1,2,3\},$$

  where $\bar{x}_{i}=(1 / n) \sum_{j} x_{i j}$, the $\epsilon_{i j}$ are independent and identically distributed as $N\left(0, \sigma^{2}\right)$, and $\sigma^{2}$ is unknown. Let $\bar{y}_{i}=(1 / n) \sum_{j} y_{i j}$.

  (i) Find expressions for $\hat{\alpha}_{i}$ and $\hat{\beta}_{i}$, the least squares estimates of $\alpha_{i}$ and $\beta_{i}$.

  (ii) What are the distributions of $\hat{\alpha}_{i}$ and $\hat{\beta}_{i}$ ?

  (iii) Show that the residual sum of squares, $R_{1}$, is given by

  $$R_{1}=\sum_{i=1}^{3}\left[\sum_{j=1}^{n}\left(y_{i j}-\bar{y}_{i}\right)^{2}-\hat{\beta}_{i}^{2} \sum_{j=1}^{n}\left(x_{i j}-\bar{x}_{i}\right)^{2}\right]$$

  Calculate $R_{1}$ when $n=9,\left\{\hat{\alpha}_{i}\right\}_{i=1}^{3}=\{1.6,0.6,0.8\},\left\{\hat{\beta}_{i}\right\}_{i=1}^{3}=\{2,1,1\}$,

  $$\left\{\sum_{j=1}^{9}\left(y_{i j}-\bar{y}_{i}\right)^{2}\right\}_{i=1}^{3}=\{138,82,63\}, \quad\left\{\sum_{j=1}^{9}\left(x_{i j}-\bar{x}_{i}\right)^{2}\right\}_{i=1}^{3}=\{30,60,40\}$$

  (iv) $H_{0}$ is the hypothesis that $\alpha_{1}=\alpha_{2}=\alpha_{3}$. Find an expression for the maximum likelihood estimator of $\alpha_{1}$ under the assumption that $H_{0}$ is true. Calculate its value for the above data.

  (v) Explain (stating without proof any relevant theory) the rationale for a statistic which can be referred to an $F$ distribution to test $H_{0}$ against the alternative that it is not true. What should be the degrees of freedom of this $F$ distribution? What would be the outcome of a size $0.05$ test of $H_{0}$ with the above data?

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2012

  State and prove the Neyman-Pearson lemma.

  A sample of two independent observations, $\left(x_{1}, x_{2}\right)$, is taken from a distribution with density $f(x ; \theta)=\theta x^{\theta-1}, 0 \leqslant x \leqslant 1$. It is desired to test $H_{0}: \theta=1$ against $H_{1}: \theta=2$. Show that the best test of size $\alpha$ can be expressed using the number $c$ such that

  $$1-c+c \log c=\alpha .$$

  Is this the uniformly most powerful test of size $\alpha$ for testing $H_{0}$ against $H_{1}: \theta>1 ?$

  Suppose that the prior distribution of $\theta$ is $P(\theta=1)=4 \gamma /(1+4 \gamma), P(\theta=2)=$ $1 /(1+4 \gamma)$, where $1>\gamma>0$. Find the test of $H_{0}$ against $H_{1}$ that minimizes the probability of error.

  Let $w(\theta)$ denote the power function of this test at $\theta(\geqslant 1)$. Show that

  $$w(\theta)=1-\gamma^{\theta}+\gamma^{\theta} \log \gamma^{\theta}$$

  comment

• Paper 3, Section II, H

  Statistics

  Part IB, 2012

  Suppose that $X$ is a single observation drawn from the uniform distribution on the interval $[\theta-10, \theta+10]$, where $\theta$ is unknown and might be any real number. Given $\theta_{0} \neq 20$ we wish to test $H_{0}: \theta=\theta_{0}$ against $H_{1}: \theta=20$. Let $\phi\left(\theta_{0}\right)$ be the test which accepts $H_{0}$ if and only if $X \in A\left(\theta_{0}\right)$, where

  $$A\left(\theta_{0}\right)= \begin{cases}{\left[\theta_{0}-8, \infty\right),} & \theta_{0}>20 \\ \left(-\infty, \theta_{0}+8\right], & \theta_{0}<20\end{cases}$$

  Show that this test has size $\alpha=0.10$.

  Now consider

  $$\begin{aligned} &C_{1}(X)=\{\theta: X \in A(\theta)\} \\ &C_{2}(X)=\{\theta: X-9 \leqslant \theta \leqslant X+9\} \end{aligned}$$

  Prove that both $C_{1}(X)$ and $C_{2}(X)$ specify $90 \%$ confidence intervals for $\theta$. Find the confidence interval specified by $C_{1}(X)$ when $X=0$.

  Let $L_{i}(X)$ be the length of the confidence interval specified by $C_{i}(X)$. Let $\beta\left(\theta_{0}\right)$ be the probability of the Type II error of $\phi\left(\theta_{0}\right)$. Show that

  $$E\left[L_{1}(X) \mid \theta=20\right]=E\left[\int_{-\infty}^{\infty} 1_{\left\{\theta_{0} \in C_{1}(X)\right\}} d \theta_{0} \mid \theta=20\right]=\int_{-\infty}^{\infty} \beta\left(\theta_{0}\right) d \theta_{0}$$

  Here $1_{\{B\}}$ is an indicator variable for event $B$. The expectation is over $X$. [Orders of integration and expectation can be interchanged.]

  Use what you know about constructing best tests to explain which of the two confidence intervals has the smaller expected length when $\theta=20$.

  comment

• Paper 1, Section I, H

  Statistics

  Part IB, 2013

  Let $x_{1}, \ldots, x_{n}$ be independent and identically distributed observations from a distribution with probability density function

  $$f(x)= \begin{cases}\lambda e^{-\lambda(x-\mu)}, & x \geqslant \mu \\ 0, & x<\mu\end{cases}$$

  where $\lambda$ and $\mu$ are unknown positive parameters. Let $\beta=\mu+1 / \lambda$. Find the maximum likelihood estimators $\hat{\lambda}, \hat{\mu}$ and $\hat{\beta}$.

  Determine for each of $\hat{\lambda}, \hat{\mu}$ and $\hat{\beta}$ whether or not it has a positive bias.

  comment

• Paper 2, Section I, H

  Statistics

  Part IB, 2013

  State and prove the Rao-Blackwell theorem.

  Individuals in a population are independently of three types $\{0,1,2\}$, with unknown probabilities $p_{0}, p_{1}, p_{2}$ where $p_{0}+p_{1}+p_{2}=1$. In a random sample of $n$ people the $i$ th person is found to be of type $x_{i} \in\{0,1,2\}$.

  Show that an unbiased estimator of $\theta=p_{0} p_{1} p_{2}$ is

  $$\hat{\theta}= \begin{cases}1, & \text { if }\left(x_{1}, x_{2}, x_{3}\right)=(0,1,2) \\ 0, & \text { otherwise. }\end{cases}$$

  Suppose that $n_{i}$ of the individuals are of type $i$. Find an unbiased estimator of $\theta$, say $\theta^{*}$, such that $\operatorname{var}\left(\theta^{*}\right)<\theta(1-\theta)$.

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2013

  Explain the notion of a sufficient statistic.

  Suppose $X$ is a random variable with distribution $F$ taking values in $\{1, \ldots, 6\}$, with $P(X=i)=p_{i}$. Let $x_{1}, \ldots, x_{n}$ be a sample from $F$. Suppose $n_{i}$ is the number of these $x_{j}$ that are equal to $i$. Use a factorization criterion to explain why $\left(n_{1}, \ldots, n_{6}\right)$ is sufficient for $\theta=\left(p_{1}, \ldots, p_{6}\right)$.

  Let $H_{0}$ be the hypothesis that $p_{i}=1 / 6$ for all $i$. Derive the statistic of the generalized likelihood ratio test of $H_{0}$ against the alternative that this is not a good fit.

  Assuming that $n_{i} \approx n / 6$ when $H_{0}$ is true and $n$ is large, show that this test can be approximated by a chi-squared test using a test statistic

  $$T=-n+\frac{6}{n} \sum_{i=1}^{6} n_{i}^{2}$$

  Suppose $n=100$ and $T=8.12$. Would you reject $H_{0} ?$ Explain your answer.

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2013

  Consider the general linear model $Y=X \theta+\epsilon$ where $X$ is a known $n \times p$ matrix, $\theta$ is an unknown $p \times 1$ vector of parameters, and $\epsilon$ is an $n \times 1$ vector of independent $N\left(0, \sigma^{2}\right)$ random variables with unknown variance $\sigma^{2}$. Assume the $p \times p$ matrix $X^{T} X$ is invertible. Let

  $$\begin{aligned} \hat{\theta} &=\left(X^{T} X\right)^{-1} X^{T} Y \\ \hat{\epsilon} &=Y-X \hat{\theta} \end{aligned}$$

  What are the distributions of $\hat{\theta}$ and $\hat{\epsilon}$ ? Show that $\hat{\theta}$ and $\hat{\epsilon}$ are uncorrelated.

  Four apple trees stand in a $2 \times 2$ rectangular grid. The annual yield of the tree at coordinate $(i, j)$ conforms to the model

  $$y_{i j}=\alpha_{i}+\beta x_{i j}+\epsilon_{i j}, \quad i, j \in\{1,2\},$$

  where $x_{i j}$ is the amount of fertilizer applied to tree $(i, j), \alpha_{1}, \alpha_{2}$ may differ because of varying soil across rows, and the $\epsilon_{i j}$ are $N\left(0, \sigma^{2}\right)$ random variables that are independent of one another and from year to year. The following two possible experiments are to be compared:

  $$\mathrm{I}:\left(x_{i j}\right)=\left(\begin{array}{cc} 0 & 1 \\ 2 & 3 \end{array}\right) \quad \text { and } \quad \mathrm{II}:\left(x_{i j}\right)=\left(\begin{array}{cc} 0 & 2 \\ 3 & 1 \end{array}\right) \text {. }$$

  Represent these as general linear models, with $\theta=\left(\alpha_{1}, \alpha_{2}, \beta\right)$. Compare the variances of estimates of $\beta$ under I and II.

  With II the following yields are observed:

  $$\left(y_{i j}\right)=\left(\begin{array}{ll} 100 & 300 \\ 600 & 400 \end{array}\right)$$

  Forecast the total yield that will be obtained next year if no fertilizer is used. What is the $95 \%$ predictive interval for this yield?

  comment

• Paper 3, Section II, H

  Statistics

  Part IB, 2013

  Suppose $x_{1}$ is a single observation from a distribution with density $f$ over $[0,1]$. It is desired to test $H_{0}: f(x)=1$ against $H_{1}: f(x)=2 x$.

  Let $\delta:[0,1] \rightarrow\{0,1\}$ define a test by $\delta\left(x_{1}\right)=i \Longleftrightarrow$ 'accept $H_{i}$ '. Let $\alpha_{i}(\delta)=P\left(\delta\left(x_{1}\right)=1-i \mid H_{i}\right)$. State the Neyman-Pearson lemma using this notation.

  Let $\delta$ be the best test of size $0.10$. Find $\delta$ and $\alpha_{1}(\delta)$.

  Consider now $\delta:[0,1] \rightarrow\{0,1, \star\}$ where $\delta\left(x_{1}\right)=\star$ means 'declare the test to be inconclusive'. Let $\gamma_{i}(\delta)=P\left(\delta(x)=\star \mid H_{i}\right)$. Given prior probabilities $\pi_{0}$ for $H_{0}$ and $\pi_{1}=1-\pi_{0}$ for $H_{1}$, and some $w_{0}, w_{1}$, let

  $$\operatorname{cost}(\delta)=\pi_{0}\left(w_{0} \alpha_{0}(\delta)+\gamma_{0}(\delta)\right)+\pi_{1}\left(w_{1} \alpha_{1}(\delta)+\gamma_{1}(\delta)\right)$$

  Let $\delta^{*}\left(x_{1}\right)=i \Longleftrightarrow x_{1} \in A_{i}$, where $A_{0}=[0,0.5), A_{\star}=[0.5,0.6), A_{1}=[0.6,1]$. Prove that for each value of $\pi_{0} \in(0,1)$ there exist $w_{0}, w_{1}$ (depending on $\left.\pi_{0}\right)$ such that $\operatorname{cost}\left(\delta^{*}\right)=\min _{\delta} \operatorname{cost}(\delta) .\left[\right.$ Hint $\left.: w_{0}=1+2(0.6)\left(\pi_{1} / \pi_{0}\right) .\right]$

  Hence prove that if $\delta$ is any test for which

  $$\alpha_{i}(\delta) \leqslant \alpha_{i}\left(\delta^{*}\right), \quad i=0,1$$

  then $\gamma_{0}(\delta) \geqslant \gamma_{0}\left(\delta^{*}\right)$ and $\gamma_{1}(\delta) \geqslant \gamma_{1}\left(\delta^{*}\right)$.

  comment

• Paper 1, Section I, $\mathbf{7 H} \quad$

  Statistics

  Part IB, 2014

  Consider an estimator $\hat{\theta}$ of an unknown parameter $\theta$, and assume that $\mathbb{E}_{\theta}\left(\hat{\theta}^{2}\right)<\infty$ for all $\theta$. Define the bias and mean squared error of $\hat{\theta}$.

  Show that the mean squared error of $\hat{\theta}$ is the sum of its variance and the square of its bias.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables with mean $\theta$ and variance $\theta^{2}$, and consider estimators of $\theta$ of the form $k \bar{X}$ where $\bar{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i}$.

  (i) Find the value of $k$ that gives an unbiased estimator, and show that the mean squared error of this unbiased estimator is $\theta^{2} / n$.

  (ii) Find the range of values of $k$ for which the mean squared error of $k \bar{X}$ is smaller $\operatorname{than} \theta^{2} / n$.

  comment

• Paper 2, Section I, H

  Statistics

  Part IB, 2014

  There are 100 patients taking part in a trial of a new surgical procedure for a particular medical condition. Of these, 50 patients are randomly selected to receive the new procedure and the remaining 50 receive the old procedure. Six months later, a doctor assesses whether or not each patient has fully recovered. The results are shown below:

  \begin{tabular}{l|c|c} & Fully recovered & Not fully recovered \ \hline Old procedure & 25 & 25 \ \hline New procedure & 31 & 19 \end{tabular}

  The doctor is interested in whether there is a difference in full recovery rates for patients receiving the two procedures. Carry out an appropriate $5 \%$ significance level test, stating your hypotheses carefully. [You do not need to derive the test.] What conclusion should be reported to the doctor?

  [Hint: Let $\chi_{k}^{2}(\alpha)$ denote the upper $100 \alpha$ percentage point of a $\chi_{k}^{2}$ distribution. Then

  $$\left.\chi_{1}^{2}(0.05)=3.84, \chi_{2}^{2}(0.05)=5.99, \chi_{3}^{2}(0.05)=7.82, \chi_{4}^{2}(0.05)=9.49 .\right]$$

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2014

  Consider a linear model

  $$\mathbf{Y}=X \boldsymbol{\beta}+\varepsilon$$

  where $X$ is a known $n \times p$ matrix, $\boldsymbol{\beta}$ is a $p \times 1(p<n)$ vector of unknown parameters and $\varepsilon$ is an $n \times 1$ vector of independent $N\left(0, \sigma^{2}\right)$ random variables with $\sigma^{2}$ unknown. Assume that $X$ has full rank $p$. Find the least squares estimator $\hat{\boldsymbol{\beta}}$ of $\boldsymbol{\beta}$ and derive its distribution. Define the residual sum of squares $R S S$ and write down an unbiased estimator $\hat{\sigma}^{2}$ of $\sigma^{2}$.

  Suppose that $V_{i}=a+b u_{i}+\delta_{i}$ and $Z_{i}=c+d w_{i}+\eta_{i}$, for $i=1, \ldots, m$, where $u_{i}$ and $w_{i}$ are known with $\sum_{i=1}^{m} u_{i}=\sum_{i=1}^{m} w_{i}=0$, and $\delta_{1}, \ldots, \delta_{m}, \eta_{1}, \ldots, \eta_{m}$ are independent $N\left(0, \sigma^{2}\right)$ random variables. Assume that at least two of the $u_{i}$ are distinct and at least two of the $w_{i}$ are distinct. Show that $\mathbf{Y}=\left(V_{1}, \ldots, V_{m}, Z_{1}, \ldots, Z_{m}\right)^{T}$ (where $T$ denotes transpose) may be written as in ( $\dagger$ ) and identify $X$ and $\boldsymbol{\beta}$. Find $\hat{\boldsymbol{\beta}}$ in terms of the $V_{i}, Z_{i}$, $u_{i}$ and $w_{i}$. Find the distribution of $\hat{b}-\hat{d}$ and derive a $95 \%$ confidence interval for $b-d$.

  [Hint: You may assume that $\frac{R S S}{\sigma^{2}}$ has a $\chi_{n-p}^{2}$ distribution, and that $\hat{\beta}$ and the residual sum of squares are independent. Properties of $\chi^{2}$ distributions may be used without proof.]

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2014

  Suppose that $X_{1}, X_{2}$, and $X_{3}$ are independent identically distributed Poisson random variables with expectation $\theta$, so that

  $$\mathbb{P}\left(X_{i}=x\right)=\frac{e^{-\theta} \theta^{x}}{x !} \quad x=0,1, \ldots$$

  and consider testing $H_{0}: \theta=1$ against $H_{1}: \theta=\theta_{1}$, where $\theta_{1}$ is a known value greater than 1. Show that the test with critical region $\left\{\left(x_{1}, x_{2}, x_{3}\right): \sum_{i=1}^{3} x_{i}>5\right\}$ is a likelihood ratio test of $H_{0}$ against $H_{1}$. What is the size of this test? Write down an expression for its power.

  A scientist counts the number of bird territories in $n$ randomly selected sections of a large park. Let $Y_{i}$ be the number of bird territories in the $i$ th section, and suppose that $Y_{1}, \ldots, Y_{n}$ are independent Poisson random variables with expectations $\theta_{1}, \ldots, \theta_{n}$ respectively. Let $a_{i}$ be the area of the $i$ th section. Suppose that $n=2 m$, $a_{1}=\cdots=a_{m}=a(>0)$ and $a_{m+1}=\cdots=a_{2 m}=2 a$. Derive the generalised likelihood ratio $\Lambda$ for testing

  $$H_{0}: \theta_{i}=\lambda a_{i} \text { against } H_{1}: \theta_{i}= \begin{cases}\lambda_{1} & i=1, \ldots, m \\ \lambda_{2} & i=m+1, \ldots, 2 m\end{cases}$$

  What should the scientist conclude about the number of bird territories if $2 \log _{e}(\Lambda)$ is $15.67 ?$

  [Hint: Let $F_{\theta}(x)$ be $\mathbb{P}(W \leqslant x)$ where $W$ has a Poisson distribution with expectation $\theta$. Then

  $$\left.F_{1}(3)=0.998, \quad F_{3}(5)=0.916, \quad F_{3}(6)=0.966, \quad F_{5}(3)=0.433 .\right]$$

  comment

• Paper 3, Section II, H

  Statistics

  Part IB, 2014

  Suppose that $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables with

  $$\mathbb{P}\left(X_{i}=x\right)=\left(\begin{array}{c} k \\ x \end{array}\right) \theta^{x}(1-\theta)^{k-x}, \quad x=0, \ldots, k$$

  where $k$ is known and $\theta(0<\theta<1)$ is an unknown parameter. Find the maximum likelihood estimator $\hat{\theta}$ of $\theta$.

  Statistician 1 has prior density for $\theta$ given by $\pi_{1}(\theta)=\alpha \theta^{\alpha-1}, 0<\theta<1$, where $\alpha>1$. Find the posterior distribution for $\theta$ after observing data $X_{1}=x_{1}, \ldots, X_{n}=x_{n}$. Write down the posterior mean $\hat{\theta}_{1}^{(B)}$, and show that

  $$\hat{\theta}_{1}^{(B)}=c \hat{\theta}+(1-c) \tilde{\theta}_{1}$$

  where $\tilde{\theta}_{1}$ depends only on the prior distribution and $c$ is a constant in $(0,1)$ that is to be specified.

  Statistician 2 has prior density for $\theta$ given by $\pi_{2}(\theta)=\alpha(1-\theta)^{\alpha-1}, 0<\theta<1$. Briefly describe the prior beliefs that the two statisticians hold about $\theta$. Find the posterior mean $\hat{\theta}_{2}^{(B)}$ and show that $\hat{\theta}_{2}^{(B)}<\hat{\theta}_{1}^{(B)}$.

  Suppose that $\alpha$ increases (but $n, k$ and the $x_{i}$ remain unchanged). How do the prior beliefs of the two statisticians change? How does $c$ vary? Explain briefly what happens to $\hat{\theta}_{1}^{(B)}$ and $\hat{\theta}_{2}^{(B)}$.

  [Hint: The Beta $(\alpha, \beta)(\alpha>0, \beta>0)$ distribution has density

  $$f(x)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1}, \quad 0<x<1$$

  with expectation $\frac{\alpha}{\alpha+\beta}$ and variance $\frac{\alpha \beta}{(\alpha+\beta+1)(\alpha+\beta)^{2}}$. Here, $\Gamma(\alpha)=\int_{0}^{\infty} x^{\alpha-1} e^{-x} d x, \alpha>0$, is the Gamma function.]

  comment

• Paper 1, Section I, H

  Statistics

  Part IB, 2015

  Suppose that $X_{1}, \ldots, X_{n}$ are independent normally distributed random variables, each with mean $\mu$ and variance 1 , and consider testing $H_{0}: \mu=0$ against $H_{1}: \mu=1$. Explain what is meant by the critical region, the size and the power of a test.

  For $0<\alpha<1$, derive the test that is most powerful among all tests of size at most $\alpha$. Obtain an expression for the power of your test in terms of the standard normal distribution function $\Phi(\cdot)$.

  [Results from the course may be used without proof provided they are clearly stated.]

  comment

• Paper 2, Section I, H

  Statistics

  Part IB, 2015

  Suppose that, given $\theta$, the random variable $X$ has $\mathbb{P}(X=k)=e^{-\theta} \theta^{k} / k !$, $k=0,1,2, \ldots .$ Suppose that the prior density of $\theta$ is $\pi(\theta)=\lambda e^{-\lambda \theta}, \theta>0$, for some known $\lambda(>0)$. Derive the posterior density $\pi(\theta \mid x)$ of $\theta$ based on the observation $X=x$.

  For a given loss function $L(\theta, a)$, a statistician wants to calculate the value of $a$ that minimises the expected posterior loss

  $$\int L(\theta, a) \pi(\theta \mid x) d \theta$$

  Suppose that $x=0$. Find $a$ in terms of $\lambda$ in the following cases:

  (a) $L(\theta, a)=(\theta-a)^{2}$;

  (b) $L(\theta, a)=|\theta-a|$.

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2015

  Consider a linear model $\mathbf{Y}=X \boldsymbol{\beta}+\varepsilon$ where $\mathbf{Y}$ is an $n \times 1$ vector of observations, $X$ is a known $n \times p$ matrix, $\boldsymbol{\beta}$ is a $p \times 1(p<n)$ vector of unknown parameters and $\varepsilon$ is an $n \times 1$ vector of independent normally distributed random variables each with mean zero and unknown variance $\sigma^{2}$. Write down the log-likelihood and show that the maximum likelihood estimators $\hat{\boldsymbol{\beta}}$ and $\hat{\sigma}^{2}$ of $\boldsymbol{\beta}$ and $\sigma^{2}$ respectively satisfy

  $$X^{T} X \hat{\boldsymbol{\beta}}=X^{T} \mathbf{Y}, \quad \frac{1}{\hat{\sigma}^{4}}(\mathbf{Y}-X \hat{\boldsymbol{\beta}})^{T}(\mathbf{Y}-X \hat{\boldsymbol{\beta}})=\frac{n}{\hat{\sigma}^{2}}$$

  $(T$ denotes the transpose $)$. Assuming that $X^{T} X$ is invertible, find the solutions $\hat{\boldsymbol{\beta}}$ and $\hat{\sigma}^{2}$ of these equations and write down their distributions.

  Prove that $\hat{\boldsymbol{\beta}}$ and $\hat{\sigma}^{2}$ are independent.

  Consider the model $Y_{i j}=\mu_{i}+\gamma x_{i j}+\varepsilon_{i j}, i=1,2,3$ and $j=1,2,3$. Suppose that, for all $i, x_{i 1}=-1, x_{i 2}=0$ and $x_{i 3}=1$, and that $\varepsilon_{i j}, i, j=1,2,3$, are independent $N\left(0, \sigma^{2}\right)$ random variables where $\sigma^{2}$ is unknown. Show how this model may be written as a linear model and write down $\mathbf{Y}, X, \boldsymbol{\beta}$ and $\varepsilon$. Find the maximum likelihood estimators of $\mu_{i}$ $(i=1,2,3), \gamma$ and $\sigma^{2}$ in terms of the $Y_{i j}$. Derive a $100(1-\alpha) \%$ confidence interval for $\sigma^{2}$ and for $\mu_{2}-\mu_{1}$.

  [You may assume that, if $\mathbf{W}=\left(\mathbf{W}_{1}^{T}, \mathbf{W}_{2}^{T}\right)^{T}$ is multivariate normal with $\operatorname{cov}\left(\mathbf{W}_{1}, \mathbf{W}_{2}\right)=0$, then $\mathbf{W}_{1}$ and $\mathbf{W}_{2}$ are independent.]

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2015

  Suppose $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables each with probability mass function $\mathbb{P}\left(X_{i}=x_{i}\right)=p\left(x_{i} ; \theta\right)$, where $\theta$ is an unknown parameter. State what is meant by a sufficient statistic for $\theta$. State the factorisation criterion for a sufficient statistic. State and prove the Rao-Blackwell theorem.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables with

  $$\mathbb{P}\left(X_{i}=x_{i}\right)=\left(\begin{array}{c} m \\ x_{i} \end{array}\right) \theta^{x_{i}}(1-\theta)^{m-x_{i}}, \quad x_{i}=0, \ldots, m$$

  where $m$ is a known positive integer and $\theta$ is unknown. Show that $\tilde{\theta}=X_{1} / m$ is unbiased for $\theta$.

  Show that $T=\sum_{i=1}^{n} X_{i}$ is sufficient for $\theta$ and use the Rao-Blackwell theorem to find another unbiased estimator $\hat{\theta}$ for $\theta$, giving details of your derivation. Calculate the variance of $\hat{\theta}$ and compare it to the variance of $\tilde{\theta}$.

  A statistician cannot remember the exact statement of the Rao-Blackwell theorem and calculates $\mathbb{E}\left(T \mid X_{1}\right)$ in an attempt to find an estimator of $\theta$. Comment on the suitability or otherwise of this approach, giving your reasons.

  [Hint: If $a$ and $b$ are positive integers then, for $r=0,1, \ldots, a+b,\left(\begin{array}{c}a+b \\ r\end{array}\right)=$ $\left.\sum_{j=0}^{r}\left(\begin{array}{c}a \\ j\end{array}\right)\left(\begin{array}{c}b \\ r-j\end{array}\right) .\right]$

  comment

• Paper 3, Section II, H

  Statistics

  Part IB, 2015

  (a) Suppose that $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables, each with density $f(x)=\theta \exp (-\theta x), x>0$ for some unknown $\theta>0$. Use the generalised likelihood ratio to obtain a size $\alpha$ test of $H_{0}: \theta=1$ against $H_{1}: \theta \neq 1$.

  (b) A die is loaded so that, if $p_{i}$ is the probability of face $i$, then $p_{1}=p_{2}=\theta_{1}$, $p_{3}=p_{4}=\theta_{2}$ and $p_{5}=p_{6}=\theta_{3}$. The die is thrown $n$ times and face $i$ is observed $x_{i}$ times. Write down the likelihood function for $\theta=\left(\theta_{1}, \theta_{2}, \theta_{3}\right)$ and find the maximum likelihood estimate of $\theta$.

  Consider testing whether or not $\theta_{1}=\theta_{2}=\theta_{3}$ for this die. Find the generalised likelihood ratio statistic $\Lambda$ and show that

  $$2 \log _{e} \Lambda \approx T, \quad \text { where } T=\sum_{i=1}^{3} \frac{\left(o_{i}-e_{i}\right)^{2}}{e_{i}}$$

  where you should specify $o_{i}$ and $e_{i}$ in terms of $x_{1}, \ldots, x_{6}$. Explain how to obtain an approximate size $0.05$ test using the value of $T$. Explain what you would conclude (and why ) if $T=2.03$.

  comment

• Paper 1, Section I, H

  Statistics

  Part IB, 2016

  Let $X_{1}, \ldots, X_{n}$ be independent samples from the exponential distribution with density $f(x ; \lambda)=\lambda e^{-\lambda x}$ for $x>0$, where $\lambda$ is an unknown parameter. Find the critical region of the most powerful test of size $\alpha$ for the hypotheses $H_{0}: \lambda=1$ versus $H_{1}: \lambda=2$. Determine whether or not this test is uniformly most powerful for testing $H_{0}^{\prime}: \lambda \leqslant 1$ versus $H_{1}^{\prime}: \lambda>1$.

  comment

• Paper 2, Section I, H

  Statistics

  Part IB, 2016

  The efficacy of a new medicine was tested as follows. Fifty patients were given the medicine, and another fifty patients were given a placebo. A week later, the number of patients who got better, stayed the same, or got worse was recorded, as summarised in this table:

  \begin{tabular}{|l|c|c|} \hline & medicine & placebo \ better & 28 & 22 \ same & 4 & 16 \ worse & 18 & 12 \ \hline \end{tabular}

  Conduct a Pearson chi-squared test of size $1 \%$ of the hypothesis that the medicine and the placebo have the same effect.

  [Hint: You may find the following values relevant:

  $\left.\begin{array}{lcccccc}\text { Distribution } & \chi_{1}^{2} & \chi_{2}^{2} & \chi_{3}^{2} & \chi_{4}^{2} & \chi_{5}^{2} & \chi_{6}^{2} \\ 99 \% \text { percentile } & 6.63 & 9.21 & 11.34 & 13.3 & 15.09 & 16.81 .\end{array}\right]$

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2016

  Consider the linear regression model

  $$Y_{i}=\alpha+\beta x_{i}+\varepsilon_{i}$$

  for $i=1, \ldots, n$, where the non-zero numbers $x_{1}, \ldots, x_{n}$ are known and are such that $x_{1}+\ldots+x_{n}=0$, the independent random variables $\varepsilon_{1}, \ldots, \varepsilon_{n}$ have the $N\left(0, \sigma^{2}\right)$ distribution, and the parameters $\alpha, \beta$ and $\sigma^{2}$ are unknown.

  (a) Let $(\hat{\alpha}, \hat{\beta})$ be the maximum likelihood estimator of $(\alpha, \beta)$. Prove that for each $i$, the random variables $\hat{\alpha}, \hat{\beta}$ and $Y_{i}-\hat{\alpha}-\hat{\beta} x_{i}$ are uncorrelated. Using standard facts about the multivariate normal distribution, prove that $\hat{\alpha}, \hat{\beta}$ and $\sum_{i=1}^{n}\left(Y_{i}-\hat{\alpha}-\hat{\beta} x_{i}\right)^{2}$ are independent.

  (b) Find the critical region of the generalised likelihood ratio test of size $5 \%$ for testing $H_{0}: \alpha=0$ versus $H_{1}: \alpha \neq 0$. Prove that the power function of this test is of the form $w\left(\alpha, \beta, \sigma^{2}\right)=g(\alpha / \sigma)$ for some function $g$. [You are not required to find $g$ explicitly.]

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2016

  (a) What does it mean to say a statistic $T$ is sufficient for an unknown parameter $\theta$ ? State the factorisation criterion for sufficiency and prove it in the discrete case.

  (b) State and prove the Rao-Blackwell theorem.

  (c) Let $X_{1}, \ldots, X_{n}$ be independent samples from the uniform distribution on $[-\theta, \theta]$ for an unknown positive parameter $\theta$. Consider the two-dimensional statistic

  $$T=\left(\min _{i} X_{i}, \max _{i} X_{i}\right) .$$

  Prove that $T$ is sufficient for $\theta$. Determine, with proof, whether or not $T$ is minimally sufficient.

  comment

• Paper 3, Section II, H

  Statistics

  Part IB, 2016

  Let $X_{1}, \ldots, X_{n}$ be independent samples from the Poisson distribution with mean $\theta$.

  (a) Compute the maximum likelihood estimator of $\theta$. Is this estimator biased?

  (b) Under the assumption that $n$ is very large, use the central limit theorem to find an approximate $95 \%$ confidence interval for $\theta$. [You may use the notation $z_{\alpha}$ for the number such that $\mathbb{P}\left(Z \geqslant z_{\alpha}\right)=\alpha$ for a standard normal $\left.Z \sim N(0,1) .\right]$

  (c) Now suppose the parameter $\theta$ has the $\Gamma(k, \lambda)$ prior distribution. What is the posterior distribution? What is the Bayes point estimator for $\theta$ for the quadratic loss function $L(\theta, a)=(\theta-a)^{2} ?$ Let $X_{n+1}$ be another independent sample from the same distribution. Given $X_{1}, \ldots, X_{n}$, what is the posterior probability that $X_{n+1}=0$ ?

  [Hint: The density of the $\Gamma(k, \lambda)$ distribution is $f(x ; k, \lambda)=\lambda^{k} x^{k-1} e^{-\lambda x} / \Gamma(k)$, for $x>0$.]

  comment

• Paper 1, Section I, H

  Statistics

  Part IB, 2017

  (a) State and prove the Rao-Blackwell theorem.

  (b) Let $X_{1}, \ldots, X_{n}$ be an independent sample from $\operatorname{Poisson}(\lambda)$ with $\theta=e^{-\lambda}$ to be estimated. Show that $Y=1_{\{0\}}\left(X_{1}\right)$ is an unbiased estimator of $\theta$ and that $T=\sum_{i} X_{i}$ is a sufficient statistic.

  What is $\mathbb{E}[Y \mid T] ?$

  comment

• Paper 2, Section I, 8H

  Statistics

  Part IB, 2017

  (a) Define a $100 \gamma \%$ confidence interval for an unknown parameter $\theta$.

  (b) Let $X_{1}, \ldots, X_{n}$ be i.i.d. random variables with distribution $N(\mu, 1)$ with $\mu$ unknown. Find a $95 \%$ confidence interval for $\mu$.

  [You may use the fact that $\Phi(1.96) \simeq 0.975 .]$

  (c) Let $U_{1}, U_{2}$ be independent $U[\theta-1, \theta+1]$ with $\theta$ to be estimated. Find a $50 \%$ confidence interval for $\theta$.

  Suppose that we have two observations $u_{1}=10$ and $u_{2}=11.5$. What might be a better interval to report in this case?

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2017

  (a) State and prove the Neyman-Pearson lemma.

  (b) Let $X$ be a real random variable with density $f(x)=(2 \theta x+1-\theta) 1_{[0,1]}(x)$ with $-1 \leqslant \theta \leqslant 1 .$

  Find a most powerful test of size $\alpha$ of $H_{0}: \theta=0$ versus $H_{1}: \theta=1$.

  Find a uniformly most powerful test of size $\alpha$ of $H_{0}: \theta=0$ versus $H_{1}: \theta>0$.

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2017

  (a) Give the definitions of a sufficient and a minimal sufficient statistic $T$ for an unknown parameter $\theta$.

  Let $X_{1}, X_{2}, \ldots, X_{n}$ be an independent sample from the geometric distribution with success probability $1 / \theta$ and mean $\theta>1$, i.e. with probability mass function

  $$p(m)=\frac{1}{\theta}\left(1-\frac{1}{\theta}\right)^{m-1} \text { for } m=1,2, \ldots$$

  Find a minimal sufficient statistic for $\theta$. Is your statistic a biased estimator of $\theta ?$

  [You may use results from the course provided you state them clearly.]

  (b) Define the bias of an estimator. What does it mean for an estimator to be unbiased?

  Suppose that $Y$ has the truncated Poisson distribution with probability mass function

  $$p(y)=\left(e^{\theta}-1\right)^{-1} \cdot \frac{\theta^{y}}{y !} \quad \text { for } y=1,2, \ldots$$

  Show that the only unbiased estimator $T$ of $1-e^{-\theta}$ based on $Y$ is obtained by taking $T=0$ if $Y$ is odd and $T=2$ if $Y$ is even.

  Is this a useful estimator? Justify your answer.

  comment

• Paper 3, Section II, $\mathbf{2 0 H}$

  Statistics

  Part IB, 2017

  Consider the general linear model

  $$\boldsymbol{Y}=X \boldsymbol{\beta}+\varepsilon$$

  where $X$ is a known $n \times p$ matrix of full rank $p<n, \varepsilon \sim \mathcal{N}_{n}\left(0, \sigma^{2} I\right)$ with $\sigma^{2}$ known and $\boldsymbol{\beta} \in \mathbb{R}^{p}$ is an unknown vector.

  (a) State without proof the Gauss-Markov theorem.

  Find the maximum likelihood estimator $\widehat{\boldsymbol{\beta}}$ for $\boldsymbol{\beta}$. Is it unbiased?

  Let $\boldsymbol{\beta}^{*}$ be any unbiased estimator for $\boldsymbol{\beta}$ which is linear in $\left(Y_{i}\right)$. Show that

  $$\operatorname{var}\left(\boldsymbol{t}^{T} \widehat{\boldsymbol{\beta}}\right) \leqslant \operatorname{var}\left(\boldsymbol{t}^{T} \boldsymbol{\beta}^{*}\right)$$

  for all $\boldsymbol{t} \in \mathbb{R}^{p}$.

  (b) Suppose now that $p=1$ and that $\boldsymbol{\beta}$ and $\sigma^{2}$ are both unknown. Find the maximum likelihood estimator for $\sigma^{2}$. What is the joint distribution of $\widehat{\boldsymbol{\beta}}$ and $\widehat{\sigma}^{2}$ in this case? Justify your answer.

  comment

• Paper 1, Section I, H

  Statistics

  Part IB, 2018

  $X_{1}, X_{2}, \ldots, X_{n}$ form a random sample from a distribution whose probability density function is

  $$f(x ; \theta)=\left\{\begin{array}{cc} \frac{2 x}{\theta^{2}} & 0 \leqslant x \leqslant \theta \\ 0 & \text { otherwise } \end{array}\right.$$

  where the value of the positive parameter $\theta$ is unknown. Determine the maximum likelihood estimator of the median of this distribution.

  comment

• Paper 2, Section I, $8 \mathrm{H}$

  Statistics

  Part IB, 2018

  Define a simple hypothesis. Define the terms size and power for a test of one simple hypothesis against another. State the Neyman-Pearson lemma.

  There is a single observation of a random variable $X$ which has a probability density function $f(x)$. Construct a best test of size $0.05$ for the null hypothesis

  $$H_{0}: \quad f(x)=\frac{1}{2}, \quad-1 \leqslant x \leqslant 1,$$

  against the alternative hypothesis

  $$H_{1}: \quad f(x)=\frac{3}{4}\left(1-x^{2}\right), \quad-1 \leqslant x \leqslant 1 .$$

  Calculate the power of your test.

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2018

  (a) Consider the general linear model $Y=X \theta+\varepsilon$ where $X$ is a known $n \times p$ matrix, $\theta$ is an unknown $p \times 1$ vector of parameters, and $\varepsilon$ is an $n \times 1$ vector of independent $N\left(0, \sigma^{2}\right)$ random variables with unknown variances $\sigma^{2}$. Show that, provided the matrix $X$ is of rank $p$, the least squares estimate of $\theta$ is

  $$\hat{\theta}=\left(X^{\mathrm{T}} X\right)^{-1} X^{\mathrm{T}} Y$$

  Let

  $$\hat{\varepsilon}=Y-X \hat{\theta}$$

  What is the distribution of $\hat{\varepsilon}^{\mathrm{T}} \hat{\varepsilon}$ ? Write down, in terms of $\hat{\varepsilon}^{\mathrm{T}} \hat{\varepsilon}$, an unbiased estimator of $\sigma^{2}$.

  (b) Four points on the ground form the vertices of a plane quadrilateral with interior angles $\theta_{1}, \theta_{2}, \theta_{3}, \theta_{4}$, so that $\theta_{1}+\theta_{2}+\theta_{3}+\theta_{4}=2 \pi$. Aerial observations $Z_{1}, Z_{2}, Z_{3}, Z_{4}$ are made of these angles, where the observations are subject to independent errors distributed as $N\left(0, \sigma^{2}\right)$ random variables.

  (i) Represent the preceding model as a general linear model with observations $\left(Z_{1}, Z_{2}, Z_{3}, Z_{4}-2 \pi\right)$ and unknown parameters $\left(\theta_{1}, \theta_{2}, \theta_{3}\right)$.

  (ii) Find the least squares estimates $\hat{\theta}_{1}, \hat{\theta}_{2}, \hat{\theta}_{3}$.

  (iii) Determine an unbiased estimator of $\sigma^{2}$. What is its distribution?

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2018

  There is widespread agreement amongst the managers of the Reliable Motor Company that the number $X$ of faulty cars produced in a month has a binomial distribution

  $$P(X=s)=\left(\begin{array}{c} n \\ s \end{array}\right) p^{s}(1-p)^{n-s} \quad(s=0,1, \ldots, n ; \quad 0 \leqslant p \leqslant 1)$$

  where $n$ is the total number of cars produced in a month. There is, however, some dispute about the parameter $p$. The general manager has a prior distribution for $p$ which is uniform, while the more pessimistic production manager has a prior distribution with density $2 p$, both on the interval $[0,1]$.

  In a particular month, $s$ faulty cars are produced. Show that if the general manager's loss function is $(\hat{p}-p)^{2}$, where $\hat{p}$ is her estimate and $p$ the true value, then her best estimate of $p$ is

  $$\hat{p}=\frac{s+1}{n+2}$$

  The production manager has responsibilities different from those of the general manager, and a different loss function given by $(1-p)(\hat{p}-p)^{2}$. Find his best estimate of $p$ and show that it is greater than that of the general manager unless $s \geqslant \frac{1}{2} n$.

  [You may use the fact that for non-negative integers $\alpha, \beta$,

  $$\left.\int_{0}^{1} p^{\alpha}(1-p)^{\beta} d p=\frac{\alpha ! \beta !}{(\alpha+\beta+1) !}\right]$$

  comment

• Paper 3, Section II, H

  Statistics

  Part IB, 2018

  A treatment is suggested for a particular illness. The results of treating a number of patients chosen at random from those in a hospital suffering from the illness are shown in the following table, in which the entries $a, b, c, d$ are numbers of patients.

  $\begin{array}{lcc} & \text { Recovery } & \text { Non-recovery } \\ \text { Untreated } & a & b \\ \text { Treated } & c & d\end{array}$

  Describe the use of Pearson's $\chi^{2}$ statistic in testing whether the treatment affects recovery, and outline a justification derived from the generalised likelihood ratio statistic. Show that

  $$\chi^{2}=\frac{(a d-b c)^{2}(a+b+c+d)}{(a+b)(c+d)(a+c)(b+d)}$$

  [Hint: You may find it helpful to observe that $a(a+b+c+d)-(a+b)(a+c)=a d-b c .]$

  Comment on the use of this statistical technique when

  $$a=50, \quad b=10, \quad c=15, \quad d=5 .$$

  comment

• Paper 1, Section I, H

  Statistics

  Part IB, 2019

  Suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. $N\left(\mu, \sigma^{2}\right)$ random variables.

  (a) Compute the MLEs $\widehat{\mu}, \widehat{\sigma}^{2}$ for the unknown parameters $\mu, \sigma^{2}$.

  (b) Give the definition of an unbiased estimator. Determine whether $\widehat{\mu}, \widehat{\sigma}^{2}$ are unbiased estimators for $\mu, \sigma^{2}$.

  comment

• Paper 2, Section I, H

  Statistics

  Part IB, 2019

  Suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. coin tosses with probability $\theta$ of obtaining a head.

  (a) Compute the posterior distribution of $\theta$ given the observations $X_{1}, \ldots, X_{n}$ in the case of a uniform prior on $[0,1]$.

  (b) Give the definition of the quadratic error loss function.

  (c) Determine the value $\widehat{\theta}$of $\theta$ which minimizes the quadratic error loss function. Justify your answer. Calculate $\mathbb{E}[\hat{\theta}]$.

  [You may use that the $\beta(a, b), a, b>0$, distribution has density function on $[0,1]$ given by

  $$c_{a, b} x^{a-1}(1-x)^{b-1}$$

  where $c_{a, b}$ is a normalizing constant. You may also use without proof that the mean of a $\beta(a, b)$ random variable is $a /(a+b) .]$

  comment

• Paper 4, Section II, 19H

  Statistics

  Part IB, 2019

  Consider the linear model

  $$Y_{i}=\beta x_{i}+\epsilon_{i} \quad \text { for } \quad i=1, \ldots, n$$

  where $x_{1}, \ldots, x_{n}$ are known and $\epsilon_{1}, \ldots, \epsilon_{n}$ are i.i.d. $N\left(0, \sigma^{2}\right)$. We assume that the parameters $\beta$ and $\sigma^{2}$ are unknown.

  (a) Find the MLE $\widehat{\beta}$ of $\beta$. Explain why $\widehat{\beta}$ is the same as the least squares estimator of $\beta$.

  (b) State and prove the Gauss-Markov theorem for this model.

  (c) For each value of $\theta \in \mathbb{R}$ with $\theta \neq 0$, determine the unbiased linear estimator $\tilde{\beta}$ of $\beta$ which minimizes

  $$\mathbb{E}_{\beta, \sigma^{2}}[\exp (\theta(\tilde{\beta}-\beta))]$$

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2019

  State and prove the Neyman-Pearson lemma.

  Suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. $\exp (\lambda)$ random variables where $\lambda$ is an unknown parameter. We wish to test the hypothesis $H_{0}: \lambda=\lambda_{0}$ against the hypothesis $H_{1}: \lambda=\lambda_{1}$ where $\lambda_{1}<\lambda_{0}$.

  (a) Find the critical region of the likelihood ratio test of size $\alpha$ in terms of the sample mean $\bar{X}$.

  (b) Define the power function of a hypothesis test and identify the power function in the setting described above in terms of the $\Gamma(n, \lambda)$ probability distribution function. [You may use without proof that $X_{1}+\cdots+X_{n}$ is distributed as a $\Gamma(n, \lambda)$ random variable.]

  (c) Define what it means for a hypothesis test to be uniformly most powerful. Determine whether the likelihood ratio test considered above is uniformly most powerful for testing $H_{0}: \lambda=\lambda_{0}$ against $\widetilde{H}_{1}: \lambda<\lambda_{0}$.

  comment

• Paper 3, Section II, H

  Statistics

  Part IB, 2019

  Suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. $N\left(\mu, \sigma^{2}\right)$. Let

  $$\bar{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i} \quad \text { and } \quad S_{X X}=\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}$$

  (a) Compute the distributions of $\bar{X}$ and $S_{X X}$ and show that $\bar{X}$ and $S_{X X}$ are independent.

  (b) Write down the distribution of $\sqrt{n}(\bar{X}-\mu) / \sqrt{S_{X X} /(n-1)}$.

  (c) For $\alpha \in(0,1)$, find a $100(1-\alpha) \%$ confidence interval in each of the following situations: (i) for $\mu$ when $\sigma^{2}$ is known; (ii) for $\mu$ when $\sigma^{2}$ is not known; (iii) for $\sigma^{2}$ when $\mu$ is not known.

  (d) Suppose that $\widetilde{X}_{1}, \ldots, \widetilde{X}_{\widetilde{n}}$ are i.i.d. $N\left(\widetilde{\mu}, \widetilde{\sigma}^{2}\right)$. Explain how you would use the $F$ test to test the hypothesis $H_{1}: \sigma^{2}>\tilde{\sigma}^{2}$ against the hypothesis $H_{0}: \sigma^{2}=\tilde{\sigma}^{2}$. Does the $F$ test depend on whether $\mu, \widetilde{\mu}$ are known?

  comment

• Paper 1, Section I, $\mathbf{6 H}$

  Statistics

  Part IB, 2020

  Suppose $X_{1}, \ldots, X_{n}$ are independent with distribution $N(\mu, 1)$. Suppose a prior $\mu \sim N\left(\theta, \tau^{-2}\right)$ is placed on the unknown parameter $\mu$ for some given deterministic $\theta \in \mathbb{R}$ and $\tau>0$. Derive the posterior mean.

  Find an expression for the mean squared error of this posterior mean when $\theta=0$.

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2020

  Let $X_{1}, \ldots, X_{n}$ be i.i.d. $U[0,2 \theta]$ random variables, where $\theta>0$ is unknown.

  (a) Derive the maximum likelihood estimator $\hat{\theta}$ of $\theta$.

  (b) What is a sufficient statistic? What is a minimal sufficient statistic? Is $\hat{\theta}$ sufficient for $\theta$ ? Is it minimal sufficient? Answer the same questions for the sample mean $\tilde{\theta}:=\sum_{i=1}^{n} X_{i} / n$. Briefly justify your answers.

  [You may use any result from the course provided it is stated clearly.]

  (c) Show that the mean squared errors of $\hat{\theta}$ and $\tilde{\theta}$ are respectively

  $$\frac{2 \theta^{2}}{(n+1)(n+2)} \quad \text { and } \quad \frac{\theta^{2}}{3 n} \text {. }$$

  (d) Show that for each $t \in \mathbb{R}, \lim _{n \rightarrow \infty} \mathbb{P}(n(1-\hat{\theta} / \theta) \geqslant t)=h(t)$ for a function $h$ you should specify. Give, with justification, an approximate $1-\alpha$ confidence interval for $\theta$ whose expected length is

  $$\left(\frac{n \theta}{n+1}\right)\left(\frac{\log (1 / \alpha)}{n-\log (1 / \alpha)}\right)$$

  [Hint: $\lim _{n \rightarrow \infty}\left(1-\frac{t}{n}\right)^{n}=e^{-t}$ for all $t \in \mathbb{R}$.]

  comment

• Paper 2, Section II, H

  Statistics

  Part IB, 2020

  Consider the general linear model $Y=X \beta^{0}+\varepsilon$ where $X$ is a known $n \times p$ design matrix with $p \geqslant 2, \beta^{0} \in \mathbb{R}^{p}$ is an unknown vector of parameters, and $\varepsilon \in \mathbb{R}^{n}$ is a vector of stochastic errors with $\mathbb{E}\left(\varepsilon_{i}\right)=0, \operatorname{var}\left(\varepsilon_{i}\right)=\sigma^{2}>0$ and $\operatorname{cov}\left(\varepsilon_{i}, \varepsilon_{j}\right)=0$ for all $i, j=1, \ldots, n$ with $i \neq j$. Suppose $X$ has full column rank.

  (a) Write down the least squares estimate $\hat{\beta}$ of $\beta^{0}$ and show that it minimises the least squares objective $S(\beta)=\|Y-X \beta\|^{2}$ over $\beta \in \mathbb{R}^{p}$.

  (b) Write down the variance-covariance matrix $\operatorname{cov}(\hat{\beta})$.

  (c) Let $\tilde{\beta} \in \mathbb{R}^{p}$ minimise $S(\beta)$ over $\beta \in \mathbb{R}^{p}$ subject to $\beta_{p}=0$. Let $Z$ be the $n \times(p-1)$ submatrix of $X$ that excludes the final column. Write $\operatorname{down} \operatorname{cov}(\tilde{\beta})$.

  (d) Let $P$ and $P_{0}$ be $n \times n$ orthogonal projections onto the column spaces of $X$ and $Z$ respectively. Show that for all $u \in \mathbb{R}^{n}, u^{T} P u \geqslant u^{T} P_{0} u$.

  (e) Show that for all $x \in \mathbb{R}^{p}$,

  $$\operatorname{var}\left(x^{T} \tilde{\beta}\right) \leqslant \operatorname{var}\left(x^{T} \hat{\beta}\right) .$$

  [Hint: Argue that $x=X^{T} u$ for some $u \in \mathbb{R}^{n}$.]

  comment

• Paper 1, Section I, H

  Statistics

  Part IB, 2021

  Let $X_{1}, \ldots, X_{n}$ be i.i.d. Bernoulli $(p)$ random variables, where $n \geqslant 3$ and $p \in(0,1)$ is unknown.

  (a) What does it mean for a statistic $T$ to be sufficient for $p$ ? Find such a sufficient statistic $T$.

  (b) State and prove the Rao-Blackwell theorem.

  (c) By considering the estimator $X_{1} X_{2}$ of $p^{2}$, find an unbiased estimator of $p^{2}$ that is a function of the statistic $T$ found in part (a), and has variance strictly smaller than that of $X_{1} X_{2}$.

  comment

• Paper 2, Section I, $\mathbf{6 H}$

  Statistics

  Part IB, 2021

  The efficacy of a new drug was tested as follows. Fifty patients were given the drug, and another fifty patients were given a placebo. A week later, the numbers of patients whose symptoms had gone entirely, improved, stayed the same and got worse were recorded, as summarised in the following table.

  \begin{tabular}{|c|c|c|} \hline & Drug & Placebo \ \hline symptoms gone & 14 & 6 \ improved & 21 & 19 \ same & 10 & 10 \ worse & 5 & 15 \ \hline \end{tabular}

  Conduct a $5 \%$ significance level test of the null hypothesis that the medicine and placebo have the same effect, against the alternative that their effects differ.

  [Hint: You may find some of the following values relevant:

  \begin{tabular}{|c|cccccc|} \hline Distribution & $\chi_{1}^{2}$ & $\chi_{2}^{2}$ & $\chi_{3}^{2}$ & $\chi_{4}^{2}$ & $\chi_{6}^{2}$ & $\chi_{8}^{2}$ \ \hline 95 th percentile & $3.84$ & $5.99$ & $7.81$ & $9.48$ & $12.59$ & $15.51$ \ \hline \end{tabular}

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2021

  (a) Show that if $W_{1}, \ldots, W_{n}$ are independent random variables with common $\operatorname{Exp}(1)$ distribution, then $\sum_{i=1}^{n} W_{i} \sim \Gamma(n, 1)$. [Hint: If $W \sim \Gamma(\alpha, \lambda)$ then $\mathbb{E} e^{t W}=\{\lambda /(\lambda-t)\}^{\alpha}$ if $t<\lambda$ and $\infty$ otherwise.]

  (b) Show that if $X \sim U(0,1)$ then $-\log X \sim \operatorname{Exp}(1)$.

  (c) State the Neyman-Pearson lemma.

  (d) Let $X_{1}, \ldots, X_{n}$ be independent random variables with common density proportional to $x^{\theta} \mathbf{1}_{(0,1)}(x)$ for $\theta \geqslant 0$. Find a most powerful test of size $\alpha$ of $H_{0}: \theta=0$ against $H_{1}: \theta=1$, giving the critical region in terms of a quantile of an appropriate gamma distribution. Find a uniformly most powerful test of size $\alpha$ of $H_{0}: \theta=0$ against $H_{1}: \theta>0$.

  comment

• Paper 3, Section II, $18 \mathrm{H}$

  Statistics

  Part IB, 2021

  Consider the normal linear model $Y=X \beta+\varepsilon$ where $X$ is a known $n \times p$ design matrix with $n-2>p \geqslant 1, \beta \in \mathbb{R}^{p}$ is an unknown vector of parameters, and $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$ is a vector of normal errors with each component having variance $\sigma^{2}>0$. Suppose $X$ has full column rank.

  (i) Write down the maximum likelihood estimators, $\hat{\beta}$ and $\hat{\sigma}^{2}$, for $\beta$ and $\sigma^{2}$ respectively. [You need not derive these.]

  (ii) Show that $\hat{\beta}$ is independent of $\hat{\sigma}^{2}$.

  (iii) Find the distributions of $\hat{\beta}$ and $n \hat{\sigma}^{2} / \sigma^{2}$.

  (iv) Consider the following test statistic for testing the null hypothesis $H_{0}: \beta=0$ against the alternative $\beta \neq 0$ :

  $$T:=\frac{\|\hat{\beta}\|^{2}}{n \hat{\sigma}^{2}} .$$

  Let $\lambda_{1} \geqslant \lambda_{2} \geqslant \cdots \geqslant \lambda_{p}>0$ be the eigenvalues of $X^{T} X$. Show that under $H_{0}, T$ has the same distribution as

  $$\frac{\sum_{j=1}^{p} \lambda_{j}^{-1} W_{j}}{Z}$$

  where $Z \sim \chi_{n-p}^{2}$ and $W_{1}, \ldots, W_{p}$ are independent $\chi_{1}^{2}$ random variables, independent of $Z$.

  [Hint: You may use the fact that $X=U D V^{T}$ where $U \in \mathbb{R}^{n \times p}$ has orthonormal columns, $V \in \mathbb{R}^{p \times p}$ is an orthogonal matrix and $D \in \mathbb{R}^{p \times p}$ is a diagonal matrix with $\left.D_{i i}=\sqrt{\lambda_{i}} .\right]$

  (v) Find $\mathbb{E} T$ when $\beta \neq 0$. [Hint: If $R \sim \chi_{\nu}^{2}$ with $\nu>2$, then $\mathbb{E}(1 / R)=1 /(\nu-2)$.]

  comment

• Paper 4, Section II, $\mathbf{1 7 H}$

  Statistics

  Part IB, 2021

  Suppose we wish to estimate the probability $\theta \in(0,1)$ that a potentially biased coin lands heads up when tossed. After $n$ independent tosses, we observe $X$ heads.

  (a) Write down the maximum likelihood estimator $\hat{\theta}$ of $\theta$.

  (b) Find the mean squared error $f(\theta)$ of $\hat{\theta}$ as a function of $\theta$. Compute $\sup _{\theta \in(0,1)} f(\theta)$.

  (c) Suppose a uniform prior is placed on $\theta$. Find the Bayes estimator of $\theta$ under squared error loss $L(\theta, a)=(\theta-a)^{2}$.

  (d) Now find the Bayes estimator $\tilde{\theta}$ under the $\operatorname{loss} L(\theta, a)=\theta^{\alpha-1}(1-\theta)^{\beta-1}(\theta-a)^{2}$, where $\alpha, \beta \geqslant 1$. Show that

  $$\tilde{\theta}=w \hat{\theta}+(1-w) \theta_{0},$$

  where $w$ and $\theta_{0}$ depend on $n, \alpha$ and $\beta$.

  (e) Determine the mean squared error $g_{w, \theta_{0}}(\theta)$ of $\tilde{\theta}$ as defined by $(*)$.

  (f) For what range of values of $w$ do we have $\sup _{\theta \in(0,1)} g_{w, 1 / 2}(\theta) \leqslant \sup _{\theta \in(0,1)} f(\theta)$ ?

  [Hint: The mean of a Beta $(a, b)$ distribution is $a /(a+b)$ and its density $p(u)$ at $u \in[0,1]$ is $c_{a, b} u^{a-1}(1-u)^{b-1}$, where $c_{a, b}$ is a normalising constant.]

  comment