4.II.12B
A uniform solid sphere has mass and radius . Calculate the moment of inertia of the sphere about an axis through its centre.
A long hollow circular cylinder of radius (where ) is held fixed with its axis horizontal. The sphere is held initially at rest in contact with the inner surface of the cylinder at , where and is the angle between the line joining the centre of the sphere to the cylinder axis and the downward vertical, as shown in the figure.
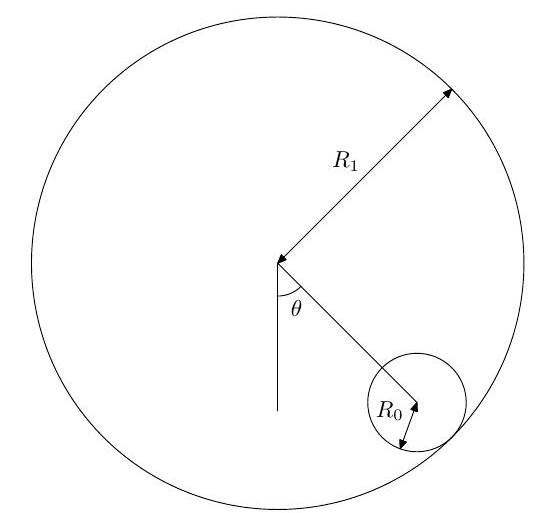
The sphere is then released, and rolls without slipping. Show that the angular velocity of the sphere is
Show further that the time, , it takes the sphere to reach is
If, instead, the cylinder and sphere surfaces are highly polished, so that the sphere now slides without rolling, find the time, , it takes to reach .
Without further calculation, explain qualitatively how your answers for and would be affected if the solid sphere were replaced by a hollow spherical shell of the same radius and mass.