Paper 2, Section II, C
An axially symmetric pulley of mass rotates about a fixed, horizontal axis, say the -axis. A string of fixed length and negligible mass connects two blocks with masses and . The string is hung over the pulley, with one mass on each side. The tensions in the string due to masses and can respectively be labelled and . The moment of inertia of the pulley is , where is a number and is the radius of the
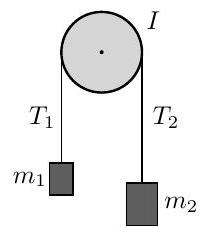
The motion of the pulley is opposed by a frictional torque of magnitude , where is the angular velocity of the pulley and is a real positive constant. Obtain a first-order differential equation for and, from it, find given that the system is released from rest.
The surface of the pulley is defined by revolving the function about the -axis, with
Find a value for the constant given that the pulley has uniform mass density .