Explain what it means for a function $f(x, y)$ of two variables to be differentiable at a point $\left(x_{0}, y_{0}\right)$. If $f$ is differentiable at $\left(x_{0}, y_{0}\right)$, show that for any $\alpha$ the function $g_{\alpha}$ defined by

$$g_{\alpha}(t)=f\left(x_{0}+t \cos \alpha, y_{0}+t \sin \alpha\right)$$

is differentiable at $t=0$, and find its derivative in terms of the partial derivatives of $f$ at $\left(x_{0}, y_{0}\right)$.

Consider the function $f$ defined by

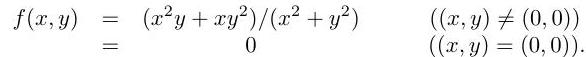
Is $f$ differentiable at $(0,0)$ ? Justify your answer.