Paper 2, Section II, H
Part IB, 2012
Let be the symmetric random walk on vertices of a connected graph. At each step this walk jumps from the current vertex to a neighbouring vertex, choosing uniformly amongst them. Let . For each let and . Stating any theorems that you use:
(i) Prove that the invariant distribution satisfies detailed balance.
(ii) Use reversibility to explain why for all .
Consider a symmetric random walk on the graph shown below.
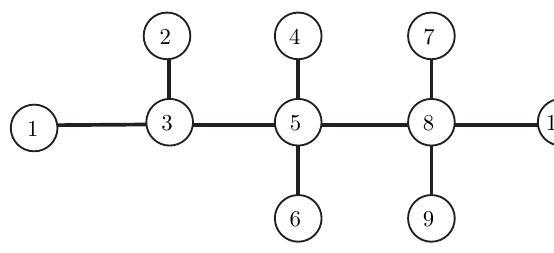
(iii) Find .
(iv) The removal of any edge leaves two disjoint components, one which includes and one which includes . Prove that , where is the number of edges in the component that contains .
(v) Show that for all .