Part IB 2015

• Paper 3, Section I, G

  Analysis II

  Part IB, 2015

  Define what is meant by a uniformly continuous function $f$ on a subset $E$ of a metric space. Show that every continuous function on a closed, bounded interval is uniformly continuous. [You may assume the Bolzano-Weierstrass theorem.]

  Suppose that a function $g:[0, \infty) \rightarrow \mathbb{R}$ is continuous and tends to a finite limit at $\infty$. Is $g$ necessarily uniformly continuous on $[0, \infty) ?$ Give a proof or a counterexample as appropriate.

  comment

• Paper 4, Section I, G

  Analysis II

  Part IB, 2015

  Define what is meant for two norms on a vector space to be Lipschitz equivalent.

  Let $C_{c}^{1}([-1,1])$ denote the vector space of continuous functions $f:[-1,1] \rightarrow \mathbb{R}$ with continuous first derivatives and such that $f(x)=0$ for $x$ in some neighbourhood of the end-points $-1$ and 1 . Which of the following four functions $C_{c}^{1}([-1,1]) \rightarrow \mathbb{R}$ define norms on $C_{c}^{1}([-1,1])$ (give a brief explanation)?

  Among those that define norms, which pairs are Lipschitz equivalent? Justify your answer.

  comment

• Paper 2, Section II, B

  Complex Analysis or Complex Methods

  Part IB, 2015

  (i) A function $f(z)$ has a pole of order $m$ at $z=z_{0}$. Derive a general expression for the residue of $f(z)$ at $z=z_{0}$ involving $f$ and its derivatives.

  (ii) Using contour integration along a contour in the upper half-plane, determine the value of the integral

  $$I=\int_{0}^{\infty} \frac{(\ln x)^{2}}{\left(1+x^{2}\right)^{2}} \mathrm{~d} x$$

  comment

• Paper 1, Section II, B

  Complex Analysis or Complex Methods

  Part IB, 2015

  (i) Show that transformations of the complex plane of the form

  $$\zeta=\frac{a z+b}{c z+d}$$

  always map circles and lines to circles and lines, where $a, b, c$ and $d$ are complex numbers such that $a d-b c \neq 0$.

  (ii) Show that the transformation

  $$\zeta=\frac{z-\alpha}{\bar{\alpha} z-1}, \quad|\alpha|<1$$

  maps the unit disk centered at $z=0$ onto itself.

  (iii) Deduce a conformal transformation that maps the non-concentric annular domain $\Omega=\{|z|<1,|z-c|>c\}, 0<c<1 / 2$, to a concentric annular domain.

  comment

• Paper 3, Section I, B

  Complex Methods

  Part IB, 2015

  Find the Fourier transform of the function

  $$f(x)=\frac{1}{1+x^{2}}, \quad x \in \mathbb{R}$$

  using an appropriate contour integration. Hence find the Fourier transform of its derivative, $f^{\prime}(x)$, and evaluate the integral

  $$I=\int_{-\infty}^{\infty} \frac{4 x^{2}}{\left(1+x^{2}\right)^{4}} d x$$

  comment

• Paper 4, Section II, B

  Complex Methods

  Part IB, 2015

  (i) State and prove the convolution theorem for Laplace transforms of two realvalued functions.

  (ii) Let the function $f(t), t \geqslant 0$, be equal to 1 for $0 \leqslant t \leqslant a$ and zero otherwise, where $a$ is a positive parameter. Calculate the Laplace transform of $f$. Hence deduce the Laplace transform of the convolution $g=f * f$. Invert this Laplace transform to obtain an explicit expression for $g(t)$.

  [Hint: You may use the notation $\left.(t-a)_{+}=H(t-a) \cdot(t-a) .\right]$

  comment

• Paper 2, Section I, A

  Electromagnetism

  Part IB, 2015

  In a constant electric field $\mathbf{E}=(E, 0,0)$ a particle of rest mass $m$ and charge $q>0$ has position $\mathbf{x}$ and velocity $\dot{\mathbf{x}}$. At time $t=0$, the particle is at rest at the origin. Including relativistic effects, calculate $\dot{\mathbf{x}}(t)$.

  Sketch a graph of $|\dot{\mathbf{x}}(t)|$ versus $t$, commenting on the $t \rightarrow \infty$ limit.

  Calculate $|\mathbf{x}(t)|$ as an explicit function of $t$ and find the non-relativistic limit at small times $t$.

  comment

• Paper 4, Section I, A

  Electromagnetism

  Part IB, 2015

  From Maxwell's equations, derive the Biot-Savart law

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int_{V} \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right) \times\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} d^{3} \mathbf{r}^{\prime}$$

  giving the magnetic field $\mathbf{B}(\mathbf{r})$ produced by a steady current density $\mathbf{J}(\mathbf{r})$ that vanishes outside a bounded region $V$.

  [You may assume that you can choose a gauge such that the divergence of the magnetic vector potential is zero.]

  comment

• Paper 1, Section II, A

  Electromagnetism

  Part IB, 2015

  (i) Write down the Lorentz force law for $d \mathbf{p} / d t$ due to an electric field $\mathbf{E}$ and magnetic field $\mathbf{B}$ acting on a particle of charge $q$ moving with velocity $\dot{\mathbf{x}}$.

  (ii) Write down Maxwell's equations in terms of $c$ (the speed of light in a vacuum), in the absence of charges and currents.

  (iii) Show that they can be manipulated into a wave equation for each component of $\mathbf{E}$.

  (iv) Show that Maxwell's equations admit solutions of the form

  $$\mathbf{E}(\mathbf{x}, t)=\operatorname{Re}\left(\mathbf{E}_{0} e^{i(\omega t-\mathbf{k} \cdot \mathbf{x})}\right)$$

  where $\mathbf{E}_{\mathbf{0}}$ and $\mathbf{k}$ are constant vectors and $\omega$ is a constant (all real). Derive a condition on $\mathbf{k} \cdot \mathbf{E}_{\mathbf{0}}$ and relate $\omega$ and $\mathbf{k}$.

  (v) Suppose that a perfect conductor occupies the region $z<0$ and that a plane wave with $\mathbf{k}=(0,0,-k), \mathbf{E}_{0}=\left(E_{0}, 0,0\right)$ is incident from the vacuum region $z>0$. Write down boundary conditions for the $\mathbf{E}$ and $\mathbf{B}$ fields. Show that they can be satisfied if a suitable reflected wave is present, and determine the total $\mathbf{E}$ and $\mathbf{B}$ fields in real form.

  (vi) At time $t=\pi /(4 \omega)$, a particle of charge $q$ and mass $m$ is at $(0,0, \pi /(4 k))$ moving with velocity $(c / 2,0,0)$. You may assume that the particle is far enough away from the conductor so that we can ignore its effect upon the conductor and that $q E_{0}>0$. Give a unit vector for the direction of the Lorentz force on the particle at time $t=\pi /(4 \omega)$.

  (vii) Ignoring relativistic effects, find the magnitude of the particle's rate of change of velocity in terms of $E_{0}, q$ and $m$ at time $t=\pi /(4 \omega)$. Why is this answer inaccurate?

  comment

• Paper 3, Section II, A

  Electromagnetism

  Part IB, 2015

  A charge density $\rho=\lambda / r$ fills the region of 3-dimensional space $a<r<b$, where $r$ is the radial distance from the origin and $\lambda$ is a constant. Compute the electric field in all regions of space in terms of $Q$, the total charge of the region. Sketch a graph of the magnitude of the electric field versus $r$ (assuming that $Q>0$ ).

  Now let $\Delta=b-a \rightarrow 0$. Derive the surface charge density $\sigma$ in terms of $\Delta, a$ and $\lambda$ and explain how a finite surface charge density may be obtained in this limit. Sketch the magnitude of the electric field versus $r$ in this limit. Comment on any discontinuities, checking a standard result involving $\sigma$ for this particular case.

  A second shell of equal and opposite total charge is centred on the origin and has a radius $c<a$. Sketch the electric potential of this system, assuming that it tends to 0 as $r \rightarrow \infty$.

  comment

• Paper 2, Section II, A

  Electromagnetism

  Part IB, 2015

  Consider the magnetic field

  $$\mathbf{B}=b[\mathbf{r}+(k \hat{\mathbf{z}}+l \hat{\mathbf{y}}) \hat{\mathbf{z}} \cdot \mathbf{r}+p \hat{\mathbf{x}}(\hat{\mathbf{y}} \cdot \mathbf{r})+n \hat{\mathbf{z}}(\hat{\mathbf{x}} \cdot \mathbf{r})],$$

  where $b \neq 0, \mathbf{r}=(x, y, z)$ and $\hat{\mathbf{x}}, \hat{\mathbf{y}}, \hat{\mathbf{z}}$ are unit vectors in the $x, y$ and $z$ directions, respectively. Imposing that this satisfies the expected equations for a static magnetic field in a vacuum, find $k, l, n$ and $p$.

  A circular wire loop of radius $a$, mass $m$ and resistance $R$ lies in the $(x, y)$ plane with its centre on the $z$-axis at $z$ and a magnetic field as given above. Calculate the magnetic flux through the loop arising from this magnetic field and also the force acting on the loop when a current $I$ is flowing around the loop in a clockwise direction about the $z$-axis.

  At $t=0$, the centre of the loop is at the origin, travelling with velocity $(0,0, v(t=0))$, where $v(0)>0$. Ignoring gravity and relativistic effects, and assuming that $I$ is only the induced current, find the time taken for the speed to halve in terms of $a, b, R$ and $m$. By what factor does the rate of heat generation change in this time?

  Where is the loop as $t \rightarrow \infty$ as a function of $a, b, R, v(0) ?$

  comment

• Paper 1, Section I, B

  Fluid Dynamics

  Part IB, 2015

  Consider a spherical bubble of radius $a$ in an inviscid fluid in the absence of gravity. The flow at infinity is at rest and the bubble undergoes translation with velocity $\mathbf{U}=U(t) \hat{\mathbf{x}}$. We assume that the flow is irrotational and derives from a potential given in spherical coordinates by

  $$\phi(r, \theta)=U(t) \frac{a^{3}}{2 r^{2}} \cos \theta,$$

  where $\theta$ is measured with respect to $\hat{\mathbf{x}}$. Compute the force, $\mathbf{F}$, acting on the bubble. Show that the formula for $\mathbf{F}$ can be interpreted as the acceleration force of a fraction $\alpha<1$ of the fluid displaced by the bubble, and determine the value of $\alpha$.

  comment

• Paper 2, Section I, G

  Analysis II

  Part IB, 2015

  Show that the map $f: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$ given by

  $$f(x, y, z)=\left(x-y-z, x^{2}+y^{2}+z^{2}, x y z\right)$$

  is differentiable everywhere and find its derivative.

  Stating accurately any theorem that you require, show that $f$ has a differentiable local inverse at a point $(x, y, z)$ if and only if

  $$(x+y)(x+z)(y-z) \neq 0 .$$

  $$\begin{aligned} & p(f)=\sup |f|, \quad q(f)=\sup \left(|f|+\left|f^{\prime}\right|\right), \\ & r(f)=\sup \left|f^{\prime}\right|, \quad s(f)=\left|\int_{-1}^{1} f(x) d x\right| \end{aligned}$$

  comment

• Paper 2, Section I, B

  Fluid Dynamics

  Part IB, 2015

  Consider the two-dimensional velocity field $\mathbf{u}=(u, v)$ with

  $$u(x, y)=x^{2}-y^{2}, \quad v(x, y)=-2 x y$$

  (i) Show that the flow is incompressible and irrotational.

  (ii) Derive the velocity potential, $\phi$, and the streamfunction, $\psi$.

  (iii) Plot all streamlines passing through the origin.

  (iv) Show that the complex function $w=\phi+i \psi$ (where $i^{2}=-1$ ) can be written solely as a function of the complex coordinate $z=x+i y$ and determine that function.

  comment

• Paper 1, Section II, B

  Fluid Dynamics

  Part IB, 2015

  A fluid layer of depth $h_{1}$ and dynamic viscosity $\mu_{1}$ is located underneath a fluid layer of depth $h_{2}$ and dynamic viscosity $\mu_{2}$. The total fluid system of depth $h=h_{1}+h_{2}$ is positioned between a stationary rigid plate at $y=0$ and a rigid plate at $y=h$ moving with speed $\mathbf{U}=U \hat{\mathbf{x}}$, where $U$ is constant. Ignore the effects of gravity.

  (i) Using dimensional analysis only, and the fact that the stress should be linear in $U$, derive the expected form of the shear stress acted by the fluid on the plate at $y=0$ as a function of $U, h_{1}, h_{2}, \mu_{1}$ and $\mu_{2}$.

  (ii) Solve for the unidirectional velocity profile between the two plates. State clearly all boundary conditions you are using to solve this problem.

  (iii) Compute the exact value of the shear stress acted by the fluid on the plate at $y=0$. Compare with the results in (i).

  (iv) What is the condition on the viscosity of the bottom layer, $\mu_{1}$, for the stress in (iii) to be smaller than it would be if the fluid had constant viscosity $\mu_{2}$ in both layers?

  (v) Show that the stress acting on the plate at $y=h$ is equal and opposite to the stress on the plate at $y=0$ and justify this result physically.

  comment

• Paper 4, Section II, B

  Fluid Dynamics

  Part IB, 2015

  Consider a steady inviscid, incompressible fluid of constant density $\rho$ in the absence of external body forces. A cylindrical jet of area $A$ and speed $U$ impinges fully on a stationary sphere of radius $R$ with $A<\pi R^{2}$. The flow is assumed to remain axisymmetric and be deflected into a conical sheet of vertex angle $\alpha>0$.

  (i) Show that the speed of the fluid in the conical sheet is constant.

  (ii) Use conservation of mass to show that the width $d(r)$ of the fluid sheet at a distance $r \gg R$ from point of impact is given by

  $$d(r)=\frac{A}{2 \pi r \sin \alpha}$$

  (iii) Use Euler's equation to derive the momentum integral equation

  $$\iint_{S}\left(p n_{i}+\rho n_{j} u_{j} u_{i}\right) d S=0$$

  for a closed surface $S$ with normal $\mathbf{n}$ where $u_{m}$ is the $m$ th component of the velocity field in cartesian coordinates and $p$ is the pressure.

  (iv) Use the result from (iii) to calculate the net force on the sphere.

  comment

• Paper 3, Section II, B

  Fluid Dynamics

  Part IB, 2015

  A source of sound induces a travelling wave of pressure above the free surface of a fluid located in the $z<0$ domain as

  $$p=p_{a t m}+p_{0} \cos (k x-\omega t),$$

  with $p_{0} \ll p_{a t m}$. Here $k$ and $\omega$ are fixed real numbers. We assume that the flow induced in the fluid is irrotational.

  (i) State the linearized equation of motion for the fluid and the free surface, $z=h(x, t)$, with all boundary conditions.

  (ii) Solve for the velocity potential, $\phi(x, z, t)$, and the height of the free surface, $h(x, t)$. Verify that your solutions are dimensionally correct.

  (iii) Interpret physically the behaviour of the solution when $\omega^{2}=g k$.

  comment

• Paper 1, Section I, F

  Geometry

  Part IB, 2015

  (i) Give a model for the hyperbolic plane. In this choice of model, describe hyperbolic lines.

  Show that if $\ell_{1}, \ell_{2}$ are two hyperbolic lines and $p_{1} \in \ell_{1}, p_{2} \in \ell_{2}$ are points, then there exists an isometry $g$ of the hyperbolic plane such that $g\left(\ell_{1}\right)=\ell_{2}$ and $g\left(p_{1}\right)=p_{2}$.

  (ii) Let $T$ be a triangle in the hyperbolic plane with angles $30^{\circ}, 30^{\circ}$ and $45^{\circ}$. What is the area of $T$ ?

  comment

• Paper 3, Section $I$, F

  Geometry

  Part IB, 2015

  State the sine rule for spherical triangles.

  Let $\Delta$ be a spherical triangle with vertices $A, B$, and $C$, with angles $\alpha, \beta$ and $\gamma$ at the respective vertices. Let $a, b$, and $c$ be the lengths of the edges $B C, A C$ and $A B$ respectively. Show that $b=c$ if and only if $\beta=\gamma$. [You may use the cosine rule for spherical triangles.] Show that this holds if and only if there exists a reflection $M$ such that $M(A)=A, M(B)=C$ and $M(C)=B$.

  Are there equilateral triangles on the sphere? Justify your answer.

  comment

• Paper 3, Section II, F

  Geometry

  Part IB, 2015

  Let $T: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ be a Möbius transformation on the Riemann sphere $\mathbb{C}_{\infty}$.

  (i) Show that $T$ has either one or two fixed points.

  (ii) Show that if $T$ is a Möbius transformation corresponding to (under stereographic projection) a rotation of $S^{2}$ through some fixed non-zero angle, then $T$ has two fixed points, $z_{1}, z_{2}$, with $z_{2}=-1 / \bar{z}_{1}$.

  (iii) Suppose $T$ has two fixed points $z_{1}, z_{2}$ with $z_{2}=-1 / \bar{z}_{1}$. Show that either $T$ corresponds to a rotation as in (ii), or one of the fixed points, say $z_{1}$, is attractive, i.e. $T^{n} z \rightarrow z_{1}$ as $n \rightarrow \infty$ for any $z \neq z_{2}$.

  comment

• Paper 2, Section II, F

  Geometry

  Part IB, 2015

  (a) For each of the following subsets of $\mathbb{R}^{3}$, explain briefly why it is a smooth embedded surface or why it is not.

  $$\begin{aligned} S_{1} &=\{(x, y, z) \mid x=y, z=3\} \cup\{(2,3,0)\} \\ S_{2} &=\left\{(x, y, z) \mid x^{2}+y^{2}-z^{2}=1\right\} \\ S_{3} &=\left\{(x, y, z) \mid x^{2}+y^{2}-z^{2}=0\right\} \end{aligned}$$

  (b) Let $f: U=\{(u, v) \mid v>0\} \rightarrow \mathbb{R}^{3}$ be given by

  $$f(u, v)=\left(u^{2}, u v, v\right),$$

  and let $S=f(U) \subseteq \mathbb{R}^{3}$. You may assume that $S$ is a smooth embedded surface.

  Find the first fundamental form of this surface.

  Find the second fundamental form of this surface.

  Compute the Gaussian curvature of this surface.

  comment

• Paper 4, Section II, F

  Geometry

  Part IB, 2015

  Let $\alpha(s)=(f(s), g(s))$ be a curve in $\mathbb{R}^{2}$ parameterized by arc length, and consider the surface of revolution $S$ in $\mathbb{R}^{3}$ defined by the parameterization

  $$\sigma(u, v)=(f(u) \cos v, f(u) \sin v, g(u))$$

  In what follows, you may use that a curve $\sigma \circ \gamma$ in $S$, with $\gamma(t)=(u(t), v(t))$, is a geodesic if and only if

  $$\ddot{u}=f(u) \frac{d f}{d u} \dot{v}^{2}, \quad \frac{d}{d t}\left(f(u)^{2} \dot{v}\right)=0$$

  (i) Write down the first fundamental form for $S$, and use this to write down a formula which is equivalent to $\sigma \circ \gamma$ being a unit speed curve.

  (ii) Show that for a given $u_{0}$, the circle on $S$ determined by $u=u_{0}$ is a geodesic if and only if $\frac{d f}{d u}\left(u_{0}\right)=0$.

  (iii) Let $\gamma(t)=(u(t), v(t))$ be a curve in $\mathbb{R}^{2}$ such that $\sigma \circ \gamma$ parameterizes a unit speed curve that is a geodesic in $S$. For a given time $t_{0}$, let $\theta\left(t_{0}\right)$ denote the angle between the curve $\sigma \circ \gamma$ and the circle on $S$ determined by $u=u\left(t_{0}\right)$. Derive Clairault's relation that

  $$f(u(t)) \cos (\theta(t))$$

  is independent of $t$.

  comment

• Paper 3, Section I, F

  Groups, Rings and Modules

  Part IB, 2015

  State two equivalent conditions for a commutative ring to be Noetherian, and prove they are equivalent. Give an example of a ring which is not Noetherian, and explain why it is not Noetherian.

  comment

• Paper 1, Section II, G

  Analysis II

  Part IB, 2015

  Define what it means for a sequence of functions $f_{n}:[0,1] \rightarrow \mathbb{R}$ to converge uniformly on $[0,1]$ to a function $f$.

  Let $f_{n}(x)=n^{p} x e^{-n^{q} x}$, where $p, q$ are positive constants. Determine all the values of $(p, q)$ for which $f_{n}(x)$ converges pointwise on $[0,1]$. Determine all the values of $(p, q)$ for which $f_{n}(x)$ converges uniformly on $[0,1]$.

  Let now $f_{n}(x)=e^{-n x^{2}}$. Determine whether or not $f_{n}$ converges uniformly on $[0,1]$.

  Let $f:[0,1] \rightarrow \mathbb{R}$ be a continuous function. Show that the sequence $x^{n} f(x)$ is uniformly convergent on $[0,1]$ if and only if $f(1)=0$.

  [If you use any theorems about uniform convergence, you should prove these.]

  comment

• Paper 4, Section I, $2 F$

  Groups, Rings and Modules

  Part IB, 2015

  Let $R$ be a commutative ring. Define what it means for an ideal $I \subseteq R$ to be prime. Show that $I \subseteq R$ is prime if and only if $R / I$ is an integral domain.

  Give an example of an integral domain $R$ and an ideal $I \subset R, I \neq R$, such that $R / I$ is not an integral domain.

  comment

• Paper 2, Section $I$, $2 F$

  Groups, Rings and Modules

  Part IB, 2015

  Give four non-isomorphic groups of order 12 , and explain why they are not isomorphic.

  comment

• Paper 1, Section II, F

  Groups, Rings and Modules

  Part IB, 2015

  (i) Give the definition of a $p$-Sylow subgroup of a group.

  (ii) Let $G$ be a group of order $2835=3^{4} \cdot 5 \cdot 7$. Show that there are at most two possibilities for the number of 3-Sylow subgroups, and give the possible numbers of 3-Sylow subgroups.

  (iii) Continuing with a group $G$ of order 2835 , show that $G$ is not simple.

  comment

• Paper 4, Section II, F

  Groups, Rings and Modules

  Part IB, 2015

  Find $a \in \mathbb{Z}_{7}$ such that $\mathbb{Z}_{7}[x] /\left(x^{3}+a\right)$ is a field $F$. Show that for your choice of $a$, every element of $\mathbb{Z}_{7}$ has a cube root in the field $F$.

  Show that if $F$ is a finite field, then the multiplicative group $F^{\times}=F \backslash\{0\}$ is cyclic.

  Show that $F=\mathbb{Z}_{2}[x] /\left(x^{3}+x+1\right)$ is a field. How many elements does $F$ have? Find a generator for $F^{\times}$.

  comment

• Paper 3, Section II, F

  Groups, Rings and Modules

  Part IB, 2015

  Can a group of order 55 have 20 elements of order 11? If so, give an example. If not, give a proof, including the proof of any statements you need.

  Let $G$ be a group of order $p q$, with $p$ and $q$ primes, $p>q$. Suppose furthermore that $q$ does not divide $p-1$. Show that $G$ is cyclic.

  comment

• Paper 2, Section II, F

  Groups, Rings and Modules

  Part IB, 2015

  (a) Consider the homomorphism $f: \mathbb{Z}^{3} \rightarrow \mathbb{Z}^{4}$ given by

  $$f(a, b, c)=(a+2 b+8 c, 2 a-2 b+4 c,-2 b+12 c, 2 a-4 b+4 c)$$

  Describe the image of this homomorphism as an abstract abelian group. Describe the quotient of $\mathbb{Z}^{4}$ by the image of this homomorphism as an abstract abelian group.

  (b) Give the definition of a Euclidean domain.

  Fix a prime $p$ and consider the subring $R$ of the rational numbers $\mathbb{Q}$ defined by

  $$R=\{q / r \mid \operatorname{gcd}(p, r)=1\}$$

  where 'gcd' stands for the greatest common divisor. Show that $R$ is a Euclidean domain.

  comment

• Paper 4, Section I, E

  Linear Algebra

  Part IB, 2015

  Define the dual space $V^{*}$ of a vector space $V$. Given a basis $\left\{x_{1}, \ldots, x_{n}\right\}$ of $V$ define its dual and show it is a basis of $V^{*}$.

  Let $V$ be a 3-dimensional vector space over $\mathbb{R}$ and let $\left\{\zeta_{1}, \zeta_{2}, \zeta_{3}\right\}$ be the basis of $V^{*}$ dual to the basis $\left\{x_{1}, x_{2}, x_{3}\right\}$ for $V$. Determine, in terms of the $\zeta_{i}$, the bases dual to each of the following: (a) $\left\{x_{1}+x_{2}, x_{2}+x_{3}, x_{3}\right\}$, (b) $\left\{x_{1}+x_{2}, x_{2}+x_{3}, x_{3}+x_{1}\right\}$.

  comment

• Paper 2, Section I, $1 \mathrm{E}$

  Linear Algebra

  Part IB, 2015

  Let $q$ denote a quadratic form on a real vector space $V$. Define the rank and signature of $q$.

  Find the rank and signature of the following quadratic forms. (a) $q(x, y, z)=x^{2}+y^{2}+z^{2}-2 x z-2 y z$. (b) $q(x, y, z)=x y-x z$.

  (c) $q(x, y, z)=x y-2 z^{2}$.

  comment

• Paper 1, Section I, E

  Linear Algebra

  Part IB, 2015

  Let $U$ and $V$ be finite dimensional vector spaces and $\alpha: U \rightarrow V$ a linear map. Suppose $W$ is a subspace of $U$. Prove that

  $$r(\alpha) \geqslant r\left(\left.\alpha\right|_{W}\right) \geqslant r(\alpha)-\operatorname{dim}(U)+\operatorname{dim}(W)$$

  where $r(\alpha)$ denotes the rank of $\alpha$ and $\left.\alpha\right|_{W}$ denotes the restriction of $\alpha$ to $W$. Give examples showing that each inequality can be both a strict inequality and an equality.

  comment

• Paper 1, Section II, E

  Linear Algebra

  Part IB, 2015

  Determine the characteristic polynomial of the matrix

  $$M=\left(\begin{array}{cccc} x & 1 & 1 & 0 \\ 1-x & 0 & -1 & 0 \\ 2 & 2 x & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

  For which values of $x \in \mathbb{C}$ is $M$ invertible? When $M$ is not invertible determine (i) the Jordan normal form $J$ of $M$, (ii) the minimal polynomial of $M$.

  Find a basis of $\mathbb{C}^{4}$ such that $J$ is the matrix representing the endomorphism $M: \mathbb{C}^{4} \rightarrow \mathbb{C}^{4}$ in this basis. Give a change of basis matrix $P$ such that $P^{-1} M P=J$.

  comment

• Paper 4, Section II, G

  Analysis II

  Part IB, 2015

  Consider the space $\ell^{\infty}$ of bounded real sequences $x=\left(x_{i}\right)_{i=1}^{\infty}$ with the norm $\|x\|_{\infty}=\sup _{i}\left|x_{i}\right|$. Show that for every bounded sequence $x^{(n)}$ in $\ell^{\infty}$ there is a subsequence $x^{\left(n_{j}\right)}$ which converges in every coordinate, i.e. the sequence $\left(x_{i}^{\left(n_{j}\right)}\right)_{j=1}^{\infty}$ of real numbers converges for each $i$. Does every bounded sequence in $\ell^{\infty}$ have a convergent subsequence? Justify your answer.

  Let $\ell^{1} \subset \ell^{\infty}$ be the subspace of real sequences $x=\left(x_{i}\right)_{i=1}^{\infty}$ such that $\sum_{i=1}^{\infty}\left|x_{i}\right|$ converges. Is $\ell^{1}$ complete in the norm $\|\cdot\|_{\infty}$ (restricted from $\ell^{\infty}$ to $\left.\ell^{1}\right)$ ? Justify your answer.

  Suppose that $\left(x_{i}\right)$ is a real sequence such that, for every $\left(y_{i}\right) \in \ell^{\infty}$, the series $\sum_{i=1}^{\infty} x_{i} y_{i}$ converges. Show that $\left(x_{i}\right) \in \ell^{1} .$

  Suppose now that $\left(x_{i}\right)$ is a real sequence such that, for every $\left(y_{i}\right) \in \ell^{1}$, the series $\sum_{i=1}^{\infty} x_{i} y_{i}$ converges. Show that $\left(x_{i}\right) \in \ell^{\infty} .$

  comment

• Paper 4, Section II, E

  Linear Algebra

  Part IB, 2015

  Suppose $U$ and $W$ are subspaces of a vector space $V$. Explain what is meant by $U \cap W$ and $U+W$ and show that both of these are subspaces of $V$.

  Show that if $U$ and $W$ are subspaces of a finite dimensional space $V$ then

  $$\operatorname{dim} U+\operatorname{dim} W=\operatorname{dim}(U \cap W)+\operatorname{dim}(U+W)$$

  Determine the dimension of the subspace $W$ of $\mathbb{R}^{5}$ spanned by the vectors

  $$\left(\begin{array}{c} 1 \\ 3 \\ 3 \\ -1 \\ 1 \end{array}\right),\left(\begin{array}{l} 4 \\ 1 \\ 3 \\ 2 \\ 1 \end{array}\right),\left(\begin{array}{l} 3 \\ 2 \\ 1 \\ 2 \\ 3 \end{array}\right),\left(\begin{array}{c} 2 \\ 2 \\ 5 \\ -1 \\ -1 \end{array}\right)$$

  Write down a $5 \times 5$ matrix which defines a linear map $\mathbb{R}^{5} \rightarrow \mathbb{R}^{5}$ with $(1,1,1,1,1)^{T}$ in the kernel and with image $W$.

  What is the dimension of the space spanned by all linear maps $\mathbb{R}^{5} \rightarrow \mathbb{R}^{5}$

  (i) with $(1,1,1,1,1)^{T}$ in the kernel and with image contained in $W$,

  (ii) with $(1,1,1,1,1)^{T}$ in the kernel or with image contained in $W$ ?

  comment

• Paper 3, Section II, E

  Linear Algebra

  Part IB, 2015

  Let $A_{1}, A_{2}, \ldots, A_{k}$ be $n \times n$ matrices over a field $\mathbb{F}$. We say $A_{1}, A_{2}, \ldots, A_{k}$ are simultaneously diagonalisable if there exists an invertible matrix $P$ such that $P^{-1} A_{i} P$ is diagonal for all $1 \leqslant i \leqslant k$. We say the matrices are commuting if $A_{i} A_{j}=A_{j} A_{i}$ for all $i, j$.

  (i) Suppose $A_{1}, A_{2}, \ldots, A_{k}$ are simultaneously diagonalisable. Prove that they are commuting.

  (ii) Define an eigenspace of a matrix. Suppose $B_{1}, B_{2}, \ldots, B_{k}$ are commuting $n \times n$ matrices over a field $\mathbb{F}$. Let $E$ denote an eigenspace of $B_{1}$. Prove that $B_{i}(E) \leqslant E$ for all $i$.

  (iii) Suppose $B_{1}, B_{2}, \ldots, B_{k}$ are commuting diagonalisable matrices. Prove that they are simultaneously diagonalisable.

  (iv) Are the $2 \times 2$ diagonalisable matrices over $\mathbb{C}$ simultaneously diagonalisable? Explain your answer.

  comment

• Paper 2, Section II, E

  Linear Algebra

  Part IB, 2015

  (i) Suppose $A$ is a matrix that does not have $-1$ as an eigenvalue. Show that $A+I$ is non-singular. Further, show that $A$ commutes with $(A+I)^{-1}$.

  (ii) A matrix $A$ is called skew-symmetric if $A^{T}=-A$. Show that a real skewsymmetric matrix does not have $-1$ as an eigenvalue.

  (iii) Suppose $A$ is a real skew-symmetric matrix. Show that $U=(I-A)(I+A)^{-1}$ is orthogonal with determinant 1 .

  (iv) Verify that every orthogonal matrix $U$ with determinant 1 which does not have $-1$ as an eigenvalue can be expressed as $(I-A)(I+A)^{-1}$ where $A$ is a real skew-symmetric matrix.

  comment

• Paper 4, Section I, H

  Markov Chains

  Part IB, 2015

  Let $X_{0}, X_{1}, X_{2}, \ldots$ be independent identically distributed random variables with $\mathbb{P}\left(X_{i}=1\right)=1-\mathbb{P}\left(X_{i}=0\right)=p, 0<p<1$. Let $Z_{n}=X_{n-1}+c X_{n}, n=1,2, \ldots$, where $c$ is a constant. For each of the following cases, determine whether or not $\left(Z_{n}: n \geqslant 1\right)$ is a Markov chain: (a) $c=0$; (b) $c=1$; (c) $c=2$.

  In each case, if $\left(Z_{n}: n \geqslant 1\right)$ is a Markov chain, explain why, and give its state space and transition matrix; if it is not a Markov chain, give an example to demonstrate that it is not.

  comment

• Paper 3, Section I, H

  Markov Chains

  Part IB, 2015

  Define what is meant by a communicating class and a closed class in a Markov chain.

  A Markov chain $\left(X_{n}: n \geqslant 0\right)$ with state space $\{1,2,3,4\}$ has transition matrix

  $$P=\left(\begin{array}{cccc} \frac{1}{2} & 0 & \frac{1}{2} & 0 \\ 0 & \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{1}{2} & 0 & \frac{1}{2} & 0 \\ \frac{1}{2} & 0 & 0 & \frac{1}{2} \end{array}\right)$$

  Write down the communicating classes for this Markov chain and state whether or not each class is closed.

  If $X_{0}=2$, let $N$ be the smallest $n$ such that $X_{n} \neq 2$. Find $\mathbb{P}(N=n)$ for $n=1,2, \ldots$ and $\mathbb{E}(N)$. Describe the evolution of the chain if $X_{0}=2$.

  comment

• Paper 2, Section II, H

  Markov Chains

  Part IB, 2015

  (a) What does it mean for a transition matrix $P$ and a distribution $\lambda$ to be in detailed balance? Show that if $P$ and $\lambda$ are in detailed balance then $\lambda=\lambda P$.

  (b) A mathematician owns $r$ bicycles, which she sometimes uses for her journey from the station to College in the morning and for the return journey in the evening. If it is fine weather when she starts a journey, and if there is a bicycle available at the current location, then she cycles; otherwise she takes the bus. Assume that with probability $p$, $0<p<1$, it is fine when she starts a journey, independently of all other journeys. Let $X_{n}$ denote the number of bicycles at the current location, just before the mathematician starts the $n$th journey.

  (i) Show that $\left(X_{n} ; n \geqslant 0\right)$ is a Markov chain and write down its transition matrix.

  (ii) Find the invariant distribution of the Markov chain.

  (iii) Show that the Markov chain satisfies the necessary conditions for the convergence theorem for Markov chains and find the limiting probability that the mathematician's $n$th journey is by bicycle.

  [Results from the course may be used without proof provided that they are clearly stated.]

  comment

• Paper 1, Section II, H

  Markov Chains

  Part IB, 2015

  Consider a particle moving between the vertices of the graph below, taking steps along the edges. Let $X_{n}$ be the position of the particle at time $n$. At time $n+1$ the particle moves to one of the vertices adjoining $X_{n}$, with each of the adjoining vertices being equally likely, independently of previous moves. Explain briefly why $\left(X_{n} ; n \geqslant 0\right)$ is a Markov chain on the vertices. Is this chain irreducible? Find an invariant distribution for this chain.

  

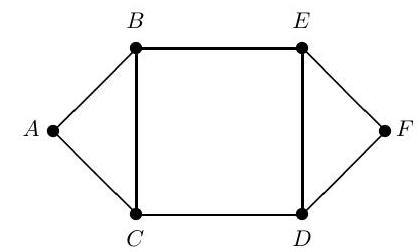
  Suppose that the particle starts at $B$. By adapting the transition matrix, or otherwise, find the probability that the particle hits vertex $A$ before vertex $F$.

  Find the expected first passage time from $B$ to $F$ given no intermediate visit to $A$.

  [Results from the course may be used without proof provided that they are clearly stated.]

  comment

• Paper 4, Section I, 5C

  Methods

  Part IB, 2015

  (a) The convolution $f * g$ of two functions $f, g: \mathbb{R} \rightarrow \mathbb{C}$ is related to their Fourier transforms $\tilde{f}, \tilde{g}$ by

  $$\frac{1}{2 \pi} \int_{-\infty}^{\infty} \tilde{f}(k) \tilde{g}(k) e^{i k x} d k=\int_{-\infty}^{\infty} f(u) g(x-u) d u$$

  Derive Parseval's theorem for Fourier transforms from this relation.

  (b) Let $a>0$ and

  $$f(x)= \begin{cases}\cos x & \text { for } x \in[-a, a] \\ 0 & \text { elsewhere }\end{cases}$$

  (i) Calculate the Fourier transform $\tilde{f}(k)$ of $f(x)$.

  (ii) Determine how the behaviour of $\tilde{f}(k)$ in the limit $|k| \rightarrow \infty$ depends on the value of $a$. Briefly interpret the result.

  comment

• Paper 2, Section I, C

  Methods

  Part IB, 2015

  (i) Write down the trigonometric form for the Fourier series and its coefficients for a function $f:[-L, L) \rightarrow \mathbb{R}$ extended to a $2 L$-periodic function on $\mathbb{R}$.

  (ii) Calculate the Fourier series on $[-\pi, \pi)$ of the function $f(x)=\sin (\lambda x)$ where $\lambda$ is a real constant. Take the limit $\lambda \rightarrow k$ with $k \in \mathbb{Z}$ in the coefficients of this series and briefly interpret the resulting expression.

  comment

• Paper 3, Section I, $7 \mathrm{C}$

  Methods

  Part IB, 2015

  (a) From the defining property of the $\delta$ function,

  $$\int_{-\infty}^{\infty} \delta(x) f(x) d x=f(0)$$

  for any function $f$, prove that

  (i) $\delta(-x)=\delta(x)$

  (ii) $\delta(a x)=|a|^{-1} \delta(x)$ for $a \in \mathbb{R}, a \neq 0$,

  (iii) If $g: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto g(x)$ is smooth and has isolated zeros $x_{i}$ where the derivative $g^{\prime}\left(x_{i}\right) \neq 0$, then

  $$\delta[g(x)]=\sum_{i} \frac{\delta\left(x-x_{i}\right)}{\left|g^{\prime}\left(x_{i}\right)\right|}$$

  (b) Show that the function $\gamma(x)$ defined by

  $$\gamma(x)=\lim _{s \rightarrow 0} \frac{e^{x / s}}{s\left(1+e^{x / s}\right)^{2}}$$

  is the $\delta(x)$ function.

  comment

• Paper 3, Section II, G

  Analysis II

  Part IB, 2015

  Define what it means for a function $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ to be differentiable at $x \in \mathbb{R}^{n}$ with derivative $D f(x)$.

  State and prove the chain rule for the derivative of $g \circ f$, where $g: \mathbb{R}^{m} \rightarrow \mathbb{R}^{p}$ is a differentiable function.

  Now let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be a differentiable function and let $g(x)=f(x, c-x)$ where $c$ is a constant. Show that $g$ is differentiable and find its derivative in terms of the partial derivatives of $f$. Show that if $D_{1} f(x, y)=D_{2} f(x, y)$ holds everywhere in $\mathbb{R}^{2}$, then $f(x, y)=h(x+y)$ for some differentiable function $h .$

  comment

• Paper 1, Section II, C

  Methods

  Part IB, 2015

  (i) Briefly describe the Sturm-Liouville form of an eigenfunction equation for real valued functions with a linear, second-order ordinary differential operator. Briefly summarize the properties of the solutions.

  (ii) Derive the condition for self-adjointness of the differential operator in (i) in terms of the boundary conditions of solutions $y_{1}, y_{2}$ to the Sturm-Liouville equation. Give at least three types of boundary conditions for which the condition for self-adjointness is satisfied.

  (iii) Consider the inhomogeneous Sturm-Liouville equation with weighted linear term

  $$\frac{1}{w(x)} \frac{d}{d x}\left(p(x) \frac{d y}{d x}\right)-\frac{q(x)}{w(x)} y-\lambda y=f(x),$$

  on the interval $a \leqslant x \leqslant b$, where $p$ and $q$ are real functions on $[a, b]$ and $w$ is the weighting function. Let $G(x, \xi)$ be a Green's function satisfying

  $$\frac{d}{d x}\left(p(x) \frac{d G}{d x}\right)-q(x) G(x, \xi)=\delta(x-\xi)$$

  Let solutions $y$ and the Green's function $G$ satisfy the same boundary conditions of the form $\alpha y^{\prime}+\beta y=0$ at $x=a, \mu y^{\prime}+\nu y=0$ at $x=b(\alpha, \beta$ are not both zero and $\mu, \nu$ are not both zero) and likewise for $G$ for the same constants $\alpha, \beta, \mu$ and $\nu$. Show that the Sturm-Liouville equation can be written as a so-called Fredholm integral equation of the form

  $$\psi(\xi)=U(\xi)+\lambda \int_{a}^{b} K(x, \xi) \psi(x) d x$$

  where $K(x, \xi)=\sqrt{w(\xi) w(x)} G(x, \xi), \psi=\sqrt{w} y$ and $U$ depends on $K, w$ and the forcing term $f$. Write down $U$ in terms of an integral involving $f, K$ and $w$.

  (iv) Derive the Fredholm integral equation for the Sturm-Liouville equation on the interval $[0,1]$

  $$\frac{d^{2} y}{d x^{2}}-\lambda y=0,$$

  with $y(0)=y(1)=0$.

  comment

• Paper 3, Section II, C

  Methods

  Part IB, 2015

  (i) Consider the Poisson equation $\nabla^{2} \psi(\mathbf{r})=f(\mathbf{r})$ with forcing term $f$ on the infinite domain $\mathbb{R}^{3}$ with $\lim _{|\mathbf{r}| \rightarrow \infty} \psi=0$. Derive the Green's function $G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=-1 /\left(4 \pi\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\right)$ for this equation using the divergence theorem. [You may assume without proof that the divergence theorem is valid for the Green's function.]

  (ii) Consider the Helmholtz equation

  $$\nabla^{2} \psi(\mathbf{r})+k^{2} \psi(\mathbf{r})=f(\mathbf{r})$$

  where $k$ is a real constant. A Green's function $g\left(\mathbf{r}, \mathbf{r}^{\prime}\right)$ for this equation can be constructed from $G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)$ of (i) by assuming $g\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=U(r) G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)$ where $r=\left|\mathbf{r}-\mathbf{r}^{\prime}\right|$ and $U(r)$ is a regular function. Show that $\lim _{r \rightarrow 0} U(r)=1$ and that $U$ satisfies the equation

  $$\frac{d^{2} U}{d r^{2}}+k^{2} U(r)=0$$

  (iii) Take the Green's function with the specific solution $U(r)=e^{i k r}$ to Eq. ( $\ddagger$ ) and consider the Helmholtz equation $(\dagger)$ on the semi-infinite domain $z>0, x, y \in \mathbb{R}$. Use the method of images to construct a Green's function for this problem that satisfies the boundary conditions

  $$\frac{\partial g}{\partial z^{\prime}}=0 \text { on } z^{\prime}=0 \quad \text { and } \quad \lim _{|\mathbf{r}| \rightarrow \infty} g\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=0$$

  (iv) A solution to the Helmholtz equation on a bounded domain can be constructed in complete analogy to that of the Poisson equation using the Green's function in Green's 3rd identity

  $$\psi(\mathbf{r})=\int_{\partial V}\left[\psi\left(\mathbf{r}^{\prime}\right) \frac{\partial g\left(\mathbf{r}, \mathbf{r}^{\prime}\right)}{\partial n^{\prime}}-g\left(\mathbf{r}, \mathbf{r}^{\prime}\right) \frac{\partial \psi\left(\mathbf{r}^{\prime}\right)}{\partial n^{\prime}}\right] d S^{\prime}+\int_{V} f\left(\mathbf{r}^{\prime}\right) g\left(\mathbf{r}, \mathbf{r}^{\prime}\right) d V^{\prime},$$

  where $V$ denotes the volume of the domain, $\partial V$ its boundary and $\partial / \partial n^{\prime}$ the outgoing normal derivative on the boundary. Now consider the homogeneous Helmholtz equation $\nabla^{2} \psi(\mathbf{r})+k^{2} \psi(\mathbf{r})=0$ on the domain $z>0, x, y \in \mathbb{R}$ with boundary conditions $\psi(\mathbf{r})=0$ at $|\mathbf{r}| \rightarrow \infty$ and

  $$\left.\frac{\partial \psi}{\partial z}\right|_{z=0}= \begin{cases}0 & \text { for } \rho>a \\ A & \text { for } \rho \leqslant a\end{cases}$$

  where $\rho=\sqrt{x^{2}+y^{2}}$ and $A$ and $a$ are real constants. Construct a solution in integral form to this equation using cylindrical coordinates $(z, \rho, \varphi)$ with $x=\rho \cos \varphi, y=\rho \sin \varphi$.

  comment

• Paper 2, Section II, C

  Methods

  Part IB, 2015

  (i) The Laplace operator in spherical coordinates is

  $$\vec{\nabla}^{2}=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2}}{\partial \phi^{2}}$$

  Show that general, regular axisymmetric solutions $\psi(r, \theta)$ to the equation $\vec{\nabla}^{2} \psi=0$ are given by

  $$\psi(r, \theta)=\sum_{n=0}^{\infty}\left(A_{n} r^{n}+B_{n} r^{-(n+1)}\right) P_{n}(\cos \theta)$$

  where $A_{n}, B_{n}$ are constants and $P_{n}$ are the Legendre polynomials. [You may use without proof that regular solutions to Legendre's equation $-\frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d}{d x} y(x)\right]=\lambda y(x)$ are given by $P_{n}(x)$ with $\lambda=n(n+1)$ and non-negative integer $n$.]

  (ii) Consider a uniformly charged wire in the form of a ring of infinitesimal width with radius $r_{0}=1$ and a constant charge per unit length $\sigma$. By Coulomb's law, the electric potential due to a point charge $q$ at a point a distance $d$ from the charge is

  $$U=\frac{q}{4 \pi \epsilon_{0} d}$$

  where $\epsilon_{0}$ is a constant. Let the $z$-axis be perpendicular to the circle and pass through the circle's centre (see figure). Show that the potential due to the charged ring at a point on the $z$-axis at location $z$ is given by

  

  $$V=\frac{\sigma}{2 \epsilon_{0} \sqrt{1+z^{2}}} .$$

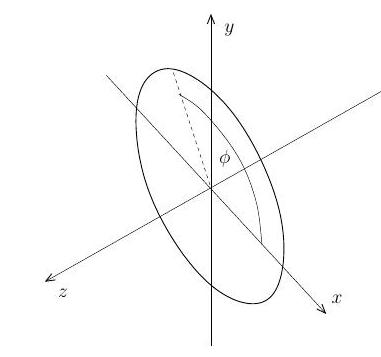
  (iii) The potential $V$ generated by the charged ring of (ii) at arbitrary points (excluding points directly on the ring which can be ignored for this question) is determined by Laplace's equation $\vec{\nabla}^{2} V=0$. Calculate this potential with the boundary condition $\lim _{r \rightarrow \infty} V=0$, where $r=\sqrt{x^{2}+y^{2}+z^{2}}$. [You may use without proof that

  $$\frac{1}{\sqrt{1+x^{2}}}=\sum_{m=0}^{\infty} x^{2 m}(-1)^{m} \frac{(2 m) !}{2^{2 m}(m !)^{2}}$$

  for $|x|<1$. Furthermore, the Legendre polynomials are normalized such that $\left.P_{n}(1)=1 .\right]$

  comment

• Paper 4, Section II, 17C

  Methods

  Part IB, 2015

  Describe the method of characteristics to construct solutions for 1st-order, homogeneous, linear partial differential equations

  $$\alpha(x, y) \frac{\partial u}{\partial x}+\beta(x, y) \frac{\partial u}{\partial y}=0$$

  with initial data prescribed on a curve $x_{0}(\sigma), y_{0}(\sigma): u\left(x_{0}(\sigma), y_{0}(\sigma)\right)=h(\sigma)$.

  Consider the partial differential equation (here the two independent variables are time $t$ and spatial direction $x$ )

  $$\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=0$$

  with initial data $u(t=0, x)=e^{-x^{2}}$.

  (i) Calculate the characteristic curves of this equation and show that $u$ remains constant along these curves. Qualitatively sketch the characteristics in the $(x, t)$ diagram, i.e. the $x$ axis is the horizontal and the $t$ axis is the vertical axis.

  (ii) Let $\tilde{x}_{0}$ denote the $x$ value of a characteristic at time $t=0$ and thus label the characteristic curves. Let $\tilde{x}$ denote the $x$ value at time $t$ of a characteristic with given $\tilde{x}_{0}$. Show that $\partial \tilde{x} / \partial \tilde{x}_{0}$ becomes a non-monotonic function of $\tilde{x}_{0}$ (at fixed $t$ ) at times $t>\sqrt{e / 2}$, i.e. $\tilde{x}\left(\tilde{x}_{0}\right)$ has a local minimum or maximum. Qualitatively sketch snapshots of the solution $u(t, x)$ for a few fixed values of $t \in[0, \sqrt{e / 2}]$ and briefly interpret the onset of the non-monotonic behaviour of $\tilde{x}\left(\tilde{x}_{0}\right)$ at $t=\sqrt{e / 2}$.

  comment

• Paper 3, Section I, $3 \mathrm{E}$

  Metric and Topological Spaces

  Part IB, 2015

  Define what it means for a topological space $X$ to be (i) connected (ii) path-connected.

  Prove that any path-connected space $X$ is connected. [You may assume the interval $[0,1]$ is connected. $]$

  Give a counterexample (without justification) to the converse statement.

  comment

• Paper 2, Section I, $4 \mathbf{E}$

  Metric and Topological Spaces

  Part IB, 2015

  Let $X$ and $Y$ be topological spaces and $f: X \rightarrow Y$ a continuous map. Suppose $H$ is a subset of $X$ such that $f(\bar{H})$ is closed (where $\bar{H}$ denotes the closure of $H$ ). Prove that $f(\bar{H})=\overline{f(H)} .$

  Give an example where $f, X, Y$ and $H$ are as above but $f(\bar{H})$ is not closed.

  comment

• Paper 1, Section II, E

  Metric and Topological Spaces

  Part IB, 2015

  Give the definition of a metric on a set $X$ and explain how this defines a topology on $X$.

  Suppose $(X, d)$ is a metric space and $U$ is an open set in $X$. Let $x, y \in X$ and $\epsilon>0$ such that the open ball $B_{\epsilon}(y) \subseteq U$ and $x \in B_{\epsilon / 2}(y)$. Prove that $y \in B_{\epsilon / 2}(x) \subseteq U$.

  Explain what it means (i) for a set $S$ to be dense in $X$, (ii) to say $\mathcal{B}$ is a base for a topology $\mathcal{T}$.

  Prove that any metric space which contains a countable dense set has a countable basis.

  comment

• Paper 4, Section II, E

  Metric and Topological Spaces

  Part IB, 2015

  Explain what it means for a metric space $(M, d)$ to be (i) compact, (ii) sequentially compact. Prove that a compact metric space is sequentially compact, stating clearly any results that you use.

  Let $(M, d)$ be a compact metric space and suppose $f: M \rightarrow M$ satisfies $d(f(x), f(y))=d(x, y)$ for all $x, y \in M$. Prove that $f$ is surjective, stating clearly any results that you use. [Hint: Consider the sequence $\left(f^{n}(x)\right)$ for $x \in M$.]

  Give an example to show that the result does not hold if $M$ is not compact.

  comment

• Paper 1, Section I, 6D

  Numerical Analysis

  Part IB, 2015

  Let

  $$A=\left[\begin{array}{rrrr} 1 & 4 & 3 & 2 \\ 4 & 17 & 13 & 11 \\ 3 & 13 & 13 & 12 \\ 2 & 11 & 12 & \lambda \end{array}\right], \quad b=\left[\begin{array}{l} 1 \\ 1 \\ 3 \\ 2 \end{array}\right]$$

  where $\lambda$ is a real parameter. Find the $L U$ factorization of the matrix $A$. Give the constraint on $\lambda$ for A to be positive definite.

  For $\lambda=18$, use this factorization to solve the system $A x=b$ via forward and backward substitution.

  comment

• Paper 4, Section I, D

  Numerical Analysis

  Part IB, 2015

  Given $n+1$ distinct points $\left\{x_{0}, x_{1}, \ldots, x_{n}\right\}$, let $p_{n} \in \mathbb{P}_{n}$ be the real polynomial of degree $n$ that interpolates a continuous function $f$ at these points. State the Lagrange interpolation formula.

  Prove that $p_{n}$ can be written in the Newton form

  $$p_{n}(x)=f\left(x_{0}\right)+\sum_{k=1}^{n} f\left[x_{0}, \ldots, x_{k}\right] \prod_{i=0}^{k-1}\left(x-x_{i}\right)$$

  where $f\left[x_{0}, \ldots, x_{k}\right]$ is the divided difference, which you should define. [An explicit expression for the divided difference is not required.]

  Explain why it can be more efficient to use the Newton form rather than the Lagrange formula.

  comment

• Paper 2, Section II, G

  Analysis II

  Part IB, 2015

  Let $E, F$ be normed spaces with norms $\|\cdot\|_{E},\|\cdot\|_{F}$. Show that for a map $f: E \rightarrow F$ and $a \in E$, the following two statements are equivalent:

  (i) For every given $\varepsilon>0$ there exists $\delta>0$ such that $\|f(x)-f(a)\|_{F}<\varepsilon$ whenever $\|x-a\|_{E}<\delta$

  (ii) $f\left(x_{n}\right) \rightarrow f(a)$ for each sequence $x_{n} \rightarrow a$.

  We say that $f$ is continuous at $a$ if (i), or equivalently (ii), holds.

  Let now $\left(E,\|\cdot\|_{E}\right)$ be a normed space. Let $A \subset E$ be a non-empty closed subset and define $d(x, A)=\inf \left\{\|x-a\|_{E}: a \in A\right\}$. Show that

  $$|d(x, A)-d(y, A)| \leqslant\|x-y\|_{E} \text { for all } x, y \in E .$$

  In the case when $E=\mathbb{R}^{n}$ with the standard Euclidean norm, show that there exists $a \in A$ such that $d(x, A)=\|x-a\|$.

  Let $A, B$ be two disjoint closed sets in $\mathbb{R}^{n}$. Must there exist disjoint open sets $U, V$ such that $A \subset U$ and $B \subset V$ ? Must there exist $a \in A$ and $b \in B$ such that $d(a, b) \leqslant d(x, y)$ for all $x \in A$ and $y \in B$ ? For each answer, give a proof or counterexample as appropriate.

  comment

• Paper 1, Section II, 18D

  Numerical Analysis

  Part IB, 2015

  Determine the real coefficients $b_{1}, b_{2}, b_{3}$ such that

  $$\int_{-2}^{2} f(x) d x=b_{1} f(-1)+b_{2} f(0)+b_{3} f(1)$$

  is exact when $f(x)$ is any real polynomial of degree 2 . Check explicitly that the quadrature is exact for $f(x)=x^{2}$ with these coefficients.

  State the Peano kernel theorem and define the Peano kernel $K(\theta)$. Use this theorem to show that if $f \in C^{3}[-2,2]$, and $b_{1}, b_{2}, b_{3}$ are chosen as above, then

  $$\left|\int_{-2}^{2} f(x) d x-b_{1} f(-1)-b_{2} f(0)-b_{3} f(1)\right| \leqslant \frac{4}{9} \max _{\xi \in[-2,2]}\left|f^{(3)}(\xi)\right|$$

  comment

• Paper 3, Section II, D

  Numerical Analysis

  Part IB, 2015

  Define the QR factorization of an $m \times n$ matrix $A$. Explain how it can be used to solve the least squares problem of finding the vector $x^{*} \in \mathbb{R}^{n}$ which minimises $\|\mathrm{A} x-b\|$, where $b \in \mathbb{R}^{m}, m>n$, and $\|\cdot\|$ is the Euclidean norm.

  Explain how to construct $Q$ and $R$ by the Gram-Schmidt procedure. Why is this procedure not useful for numerical factorization of large matrices?

  Let

  $$A=\left[\begin{array}{rrr} 5 & 6 & -14 \\ 5 & 4 & 4 \\ -5 & 2 & -8 \\ 5 & 12 & -18 \end{array}\right], \quad b=\left[\begin{array}{l} 1 \\ 1 \\ 1 \\ 0 \end{array}\right]$$

  Using the Gram-Schmidt procedure find a QR decomposition of A. Hence solve the least squares problem giving both $x^{*}$ and $\left\|\mathrm{A} x^{*}-b\right\|$.

  comment

• Paper 2, Section II, D

  Numerical Analysis

  Part IB, 2015

  Define the linear stability domain for a numerical method to solve $y^{\prime}=f(t, y)$. What is meant by an $A$-stable method? Briefly explain the relevance of these concepts in the numerical solution of ordinary differential equations.

  Consider

  $$y_{n+1}=y_{n}+h\left[\theta f\left(t_{n}, y_{n}\right)+(1-\theta) f\left(t_{n+1}, y_{n+1}\right)\right]$$

  where $\theta \in[0,1]$. What is the order of this method?

  Find the linear stability domain of this method. For what values of $\theta$ is the method A-stable?

  comment

• Paper 1, Section I, H

  Optimization

  Part IB, 2015

  (a) Consider a network with vertices in $V=\{1, \ldots, n\}$ and directed edges $(i, j)$ in $E \subseteq V \times V$. Suppose that 1 is the source and $n$ is the sink. Let $C_{i j}, 0<C_{i j}<\infty$, be the capacity of the edge from vertex $i$ to vertex $j$ for $(i, j) \in E$. Let a cut be a partition of $V=\{1, \ldots, n\}$ into $S$ and $V \backslash S$ with $1 \in S$ and $n \in V \backslash S$. Define the capacity of the cut $S$. Write down the maximum flow problem. Prove that the maximum flow is bounded above by the minimum cut capacity.

  (b) Find the maximum flow from the source to the sink in the network below, where the directions and capacities of the edges are shown. Explain your reasoning.

  

  comment

• Paper 2, Section I, H

  Optimization

  Part IB, 2015

  Define what it means to say that a set $S \subseteq \mathbb{R}^{n}$ is convex. What is meant by an extreme point of a convex set $S$ ?

  Consider the set $S \subseteq \mathbb{R}^{2}$ given by

  $$S=\left\{\left(x_{1}, x_{2}\right): x_{1}+4 x_{2} \leqslant 30,3 x_{1}+7 x_{2} \leqslant 60, x_{1} \geqslant 0, x_{2} \geqslant 0\right\}$$

  Show that $S$ is convex, and give the coordinates of all extreme points of $S$.

  For all possible choices of $c_{1}>0$ and $c_{2}>0$, find the maximum value of $c_{1} x_{1}+c_{2} x_{2}$ subject to $\left(x_{1}, x_{2}\right) \in S$.

  comment

• Paper 4, Section II, 20H

  Optimization

  Part IB, 2015

  Suppose the recycling manager in a particular region is responsible for allocating all the recyclable waste that is collected in $n$ towns in the region to the $m$ recycling centres in the region. Town $i$ produces $s_{i}$ lorry loads of recyclable waste each day, and recycling centre $j$ needs to handle $d_{j}$ lorry loads of waste a day in order to be viable. Suppose that $\sum_{i} s_{i}=\sum_{j} d_{j}$. Suppose further that $c_{i j}$ is the cost of transporting a lorry load of waste from town $i$ to recycling centre $j$. The manager wishes to decide the number $x_{i j}$ of lorry loads of recyclable waste that should go from town $i$ to recycling centre $j$, $i=1, \ldots, n, j=1, \ldots, m$, in such a way that all the recyclable waste produced by each town is transported to recycling centres each day, and each recycling centre works exactly at the viable level each day. Use the Lagrangian sufficiency theorem, which you should quote carefully, to derive necessary and sufficient conditions for $\left(x_{i j}\right)$ to minimise the total cost under the above constraints.

  Suppose that there are three recycling centres $A, B$ and $C$, needing 5,20 and 20 lorry loads of waste each day, respectively, and suppose there are three towns $a, b$ and $c$ producing 20,15 and 10 lorry loads of waste each day, respectively. The costs of transporting a lorry load of waste from town $a$ to recycling centres $A, B$ and $C$ are $£ 90, £ 100$ and $£ 100$, respectively. The corresponding costs for town $b$ are $£ 130, £ 140$ and $£ 100$, while for town $c$ they are $£ 110, £ 80$ and $£ 80$. Recycling centre $A$ has reported that it currently receives 5 lorry loads of waste per day from town $a$, and recycling centre $C$ has reported that it currently receives 10 lorry loads of waste per day from each of towns $b$ and c. Recycling centre $B$ has failed to report. What is the cost of the current arrangement for transporting waste from the towns to the recycling centres? Starting with the current arrangement as an initial solution, use the transportation algorithm (explaining each step carefully) in order to advise the recycling manager how many lorry loads of waste should go from each town to each of the recycling centres in order to minimise the cost. What is the minimum cost?

  comment

• Paper 3, Section II, H

  Optimization

  Part IB, 2015

  Consider the linear programming problem $P$ :

  $$\text { minimise } c^{T} x \text { subject to } A x \geqslant b, x \geqslant 0,$$

  where $x$ and $c$ are in $\mathbb{R}^{n}, A$ is a real $m \times n$ matrix, $b$ is in $\mathbb{R}^{m}$ and ${ }^{T}$ denotes transpose. Derive the dual linear programming problem $D$. Show from first principles that the dual of $D$ is $P$.

  Suppose that $c^{T}=(6,10,11), b^{T}=(1,1,3)$ and $A=\left(\begin{array}{lll}1 & 3 & 8 \\ 1 & 1 & 2 \\ 2 & 4 & 4\end{array}\right)$. Write down the dual $D$ and find the optimal solution of the dual using the simplex algorithm. Hence, or otherwise, find the optimal solution $x^{*}=\left(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}\right)$ of $P$.

  Suppose that $c$ is changed to $\tilde{c}=\left(6+\varepsilon_{1}, 10+\varepsilon_{2}, 11+\varepsilon_{3}\right)$. Give necessary and sufficient conditions for $x^{*}$ still to be the optimal solution of $P$. If $\varepsilon_{1}=\varepsilon_{2}=0$, find the range of values for $\varepsilon_{3}$ for which $x^{*}$ is still the optimal solution of $P$.

  comment

• Paper 4, Section I, D

  Quantum Mechanics

  Part IB, 2015

  The radial wavefunction $R(r)$ for an electron in a hydrogen atom satisfies the equation

  $$-\frac{\hbar^{2}}{2 m r^{2}} \frac{d}{d r}\left(r^{2} \frac{d}{d r} R(r)\right)+\frac{\hbar^{2}}{2 m r^{2}} \ell(\ell+1) R(r)-\frac{e^{2}}{4 \pi \epsilon_{0} r} R(r)=E R(r)$$

  Briefly explain the origin of each term in this equation.

  The wavefunctions for the ground state and the first radially excited state, both with $\ell=0$, can be written as

  $$\begin{aligned} &R_{1}(r)=N_{1} e^{-\alpha r} \\ &R_{2}(r)=N_{2}\left(1-\frac{1}{2} r \alpha\right) e^{-\frac{1}{2} \alpha r} \end{aligned}$$

  where $N_{1}$ and $N_{2}$ are normalisation constants. Verify that $R_{1}(r)$ is a solution of $(*)$, determining $\alpha$ and finding the corresponding energy eigenvalue $E_{1}$. Assuming that $R_{2}(r)$ is a solution of $(*)$, compare coefficients of the dominant terms when $r$ is large to determine the corresponding energy eigenvalue $E_{2}$. [You do not need to find $N_{1}$ or $N_{2}$, nor show that $R_{2}$ is a solution of $\left.(*) .\right]$

  A hydrogen atom makes a transition from the first radially excited state to the ground state, emitting a photon. What is the angular frequency of the emitted photon?

  comment

• Paper 3, Section $I$, D

  Quantum Mechanics

  Part IB, 2015

  A quantum-mechanical system has normalised energy eigenstates $\chi_{1}$ and $\chi_{2}$ with non-degenerate energies $E_{1}$ and $E_{2}$ respectively. The observable $A$ has normalised eigenstates,

  $$\begin{aligned} \phi_{1} &=C\left(\chi_{1}+2 \chi_{2}\right), & & \text { eigenvalue }=a_{1} \\ \phi_{2} &=C\left(2 \chi_{1}-\chi_{2}\right), & & \text { eigenvalue }=a_{2} \end{aligned}$$

  where $C$ is a positive real constant. Determine $C$.

  Initially, at time $t=0$, the state of the system is $\phi_{1}$. Write down an expression for $\psi(t)$, the state of the system with $t \geqslant 0$. What is the probability that a measurement of energy at time $t$ will yield $E_{2}$ ?

  For the same initial state, determine the probability that a measurement of $A$ at time $t>0$ will yield $a_{1}$ and the probability that it will yield $a_{2}$.

  comment

• Paper 1, Section II, D

  Quantum Mechanics

  Part IB, 2015

  Write down expressions for the probability density $\rho(x, t)$ and the probability current $j(x, t)$ for a particle in one dimension with wavefunction $\Psi(x, t)$. If $\Psi(x, t)$ obeys the timedependent Schrödinger equation with a real potential, show that

  $$\frac{\partial j}{\partial x}+\frac{\partial \rho}{\partial t}=0$$

  Consider a stationary state, $\Psi(x, t)=\psi(x) e^{-i E t / \hbar}$, with

  $$\psi(x) \sim \begin{cases}e^{i k_{1} x}+R e^{-i k_{1} x} & x \rightarrow-\infty \\ T e^{i k_{2} x} & x \rightarrow+\infty\end{cases}$$

  where $E, k_{1}, k_{2}$ are real. Evaluate $j(x, t)$ for this state in the regimes $x \rightarrow+\infty$ and $x \rightarrow-\infty$.

  Consider a real potential,

  $$V(x)=-\alpha \delta(x)+U(x), \quad U(x)= \begin{cases}0 & x<0 \\ V_{0} & x>0\end{cases}$$

  where $\delta(x)$ is the Dirac delta function, $V_{0}>0$ and $\alpha>0$. Assuming that $\psi(x)$ is continuous at $x=0$, derive an expression for

  $$\lim _{\epsilon \rightarrow 0}\left[\psi^{\prime}(\epsilon)-\psi^{\prime}(-\epsilon)\right]$$

  Hence calculate the reflection and transmission probabilities for a particle incident from $x=-\infty$ with energy $E>V_{0} .$

  comment

• Paper 4, Section I, G

  Complex Analysis

  Part IB, 2015

  Let $f$ be a continuous function defined on a connected open set $D \subset \mathbb{C}$. Prove carefully that the following statements are equivalent.

  (i) There exists a holomorphic function $F$ on $D$ such that $F^{\prime}(z)=f(z)$.

  (ii) $\int_{\gamma} f(z) d z=0$ holds for every closed curve $\gamma$ in $D$.

  comment

• Paper 3, Section II, D

  Quantum Mechanics

  Part IB, 2015

  Define the angular momentum operators $\hat{L}_{i}$ for a particle in three dimensions in terms of the position and momentum operators $\hat{x}_{i}$ and $\hat{p}_{i}=-i \hbar \frac{\partial}{\partial x_{i}}$. Write down an expression for $\left[\hat{L}_{i}, \hat{L}_{j}\right]$ and use this to show that $\left[\hat{L}^{2}, \hat{L}_{i}\right]=0$ where $\hat{L}^{2}=\hat{L}_{x}^{2}+\hat{L}_{y}^{2}+\hat{L}_{z}^{2}$. What is the significance of these two commutation relations?

  Let $\psi(x, y, z)$ be both an eigenstate of $\hat{L}_{z}$ with eigenvalue zero and an eigenstate of $\hat{L}^{2}$ with eigenvalue $\hbar^{2} l(l+1)$. Show that $\left(\hat{L}_{x}+i \hat{L}_{y}\right) \psi$ is also an eigenstate of both $\hat{L}_{z}$ and $\hat{L}^{2}$ and determine the corresponding eigenvalues.

  Find real constants $A$ and $B$ such that

  $$\phi(x, y, z)=\left(A z^{2}+B y^{2}-r^{2}\right) e^{-r}, \quad r^{2}=x^{2}+y^{2}+z^{2},$$

  is an eigenfunction of $\hat{L}_{z}$ with eigenvalue zero and an eigenfunction of $\hat{L}^{2}$ with an eigenvalue which you should determine. [Hint: You might like to show that $\left.\hat{L}_{i} f(r)=0 .\right]$

  comment

• Paper 2, Section II, D

  Quantum Mechanics

  Part IB, 2015

  A quantum-mechanical harmonic oscillator has Hamiltonian

  $$\hat{H}=\frac{\hat{p}^{2}}{2}+\frac{1}{2} k^{2} \hat{x}^{2}$$

  where $k$ is a positive real constant. Show that $\hat{x}=x$ and $\hat{p}=-i \hbar \frac{\partial}{\partial x}$ are Hermitian operators.

  The eigenfunctions of $(*)$ can be written as

  $$\psi_{n}(x)=h_{n}(x \sqrt{k / \hbar}) \exp \left(-\frac{k x^{2}}{2 \hbar}\right),$$

  where $h_{n}$ is a polynomial of degree $n$ with even (odd) parity for even (odd) $n$ and $n=0,1,2, \ldots$. Show that $\langle\hat{x}\rangle=\langle\hat{p}\rangle=0$ for all of the states $\psi_{n}$.

  State the Heisenberg uncertainty principle and verify it for the state $\psi_{0}$ by computing $(\Delta x)$ and $(\Delta p)$. [Hint: You should properly normalise the state.]

  The oscillator is in its ground state $\psi_{0}$ when the potential is suddenly changed so that $k \rightarrow 4 k$. If the wavefunction is expanded in terms of the energy eigenfunctions of the new Hamiltonian, $\phi_{n}$, what can be said about the coefficient of $\phi_{n}$ for odd $n$ ? What is the probability that the particle is in the new ground state just after the change?

  [Hint: You may assume that if $I_{n}=\int_{-\infty}^{\infty} e^{-a x^{2}} x^{n} d x$ then $I_{0}=\sqrt{\frac{\pi}{a}}$ and $I_{2}=\frac{1}{2 a} \sqrt{\frac{\pi}{a}}$.]

  comment

• Paper 1, Section I, H

  Statistics

  Part IB, 2015

  Suppose that $X_{1}, \ldots, X_{n}$ are independent normally distributed random variables, each with mean $\mu$ and variance 1 , and consider testing $H_{0}: \mu=0$ against $H_{1}: \mu=1$. Explain what is meant by the critical region, the size and the power of a test.

  For $0<\alpha<1$, derive the test that is most powerful among all tests of size at most $\alpha$. Obtain an expression for the power of your test in terms of the standard normal distribution function $\Phi(\cdot)$.

  [Results from the course may be used without proof provided they are clearly stated.]

  comment

• Paper 2, Section I, H

  Statistics

  Part IB, 2015

  Suppose that, given $\theta$, the random variable $X$ has $\mathbb{P}(X=k)=e^{-\theta} \theta^{k} / k !$, $k=0,1,2, \ldots .$ Suppose that the prior density of $\theta$ is $\pi(\theta)=\lambda e^{-\lambda \theta}, \theta>0$, for some known $\lambda(>0)$. Derive the posterior density $\pi(\theta \mid x)$ of $\theta$ based on the observation $X=x$.

  For a given loss function $L(\theta, a)$, a statistician wants to calculate the value of $a$ that minimises the expected posterior loss

  $$\int L(\theta, a) \pi(\theta \mid x) d \theta$$

  Suppose that $x=0$. Find $a$ in terms of $\lambda$ in the following cases:

  (a) $L(\theta, a)=(\theta-a)^{2}$;

  (b) $L(\theta, a)=|\theta-a|$.

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2015

  Consider a linear model $\mathbf{Y}=X \boldsymbol{\beta}+\varepsilon$ where $\mathbf{Y}$ is an $n \times 1$ vector of observations, $X$ is a known $n \times p$ matrix, $\boldsymbol{\beta}$ is a $p \times 1(p<n)$ vector of unknown parameters and $\varepsilon$ is an $n \times 1$ vector of independent normally distributed random variables each with mean zero and unknown variance $\sigma^{2}$. Write down the log-likelihood and show that the maximum likelihood estimators $\hat{\boldsymbol{\beta}}$ and $\hat{\sigma}^{2}$ of $\boldsymbol{\beta}$ and $\sigma^{2}$ respectively satisfy

  $$X^{T} X \hat{\boldsymbol{\beta}}=X^{T} \mathbf{Y}, \quad \frac{1}{\hat{\sigma}^{4}}(\mathbf{Y}-X \hat{\boldsymbol{\beta}})^{T}(\mathbf{Y}-X \hat{\boldsymbol{\beta}})=\frac{n}{\hat{\sigma}^{2}}$$

  $(T$ denotes the transpose $)$. Assuming that $X^{T} X$ is invertible, find the solutions $\hat{\boldsymbol{\beta}}$ and $\hat{\sigma}^{2}$ of these equations and write down their distributions.

  Prove that $\hat{\boldsymbol{\beta}}$ and $\hat{\sigma}^{2}$ are independent.

  Consider the model $Y_{i j}=\mu_{i}+\gamma x_{i j}+\varepsilon_{i j}, i=1,2,3$ and $j=1,2,3$. Suppose that, for all $i, x_{i 1}=-1, x_{i 2}=0$ and $x_{i 3}=1$, and that $\varepsilon_{i j}, i, j=1,2,3$, are independent $N\left(0, \sigma^{2}\right)$ random variables where $\sigma^{2}$ is unknown. Show how this model may be written as a linear model and write down $\mathbf{Y}, X, \boldsymbol{\beta}$ and $\varepsilon$. Find the maximum likelihood estimators of $\mu_{i}$ $(i=1,2,3), \gamma$ and $\sigma^{2}$ in terms of the $Y_{i j}$. Derive a $100(1-\alpha) \%$ confidence interval for $\sigma^{2}$ and for $\mu_{2}-\mu_{1}$.

  [You may assume that, if $\mathbf{W}=\left(\mathbf{W}_{1}^{T}, \mathbf{W}_{2}^{T}\right)^{T}$ is multivariate normal with $\operatorname{cov}\left(\mathbf{W}_{1}, \mathbf{W}_{2}\right)=0$, then $\mathbf{W}_{1}$ and $\mathbf{W}_{2}$ are independent.]

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2015

  Suppose $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables each with probability mass function $\mathbb{P}\left(X_{i}=x_{i}\right)=p\left(x_{i} ; \theta\right)$, where $\theta$ is an unknown parameter. State what is meant by a sufficient statistic for $\theta$. State the factorisation criterion for a sufficient statistic. State and prove the Rao-Blackwell theorem.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables with

  $$\mathbb{P}\left(X_{i}=x_{i}\right)=\left(\begin{array}{c} m \\ x_{i} \end{array}\right) \theta^{x_{i}}(1-\theta)^{m-x_{i}}, \quad x_{i}=0, \ldots, m$$

  where $m$ is a known positive integer and $\theta$ is unknown. Show that $\tilde{\theta}=X_{1} / m$ is unbiased for $\theta$.

  Show that $T=\sum_{i=1}^{n} X_{i}$ is sufficient for $\theta$ and use the Rao-Blackwell theorem to find another unbiased estimator $\hat{\theta}$ for $\theta$, giving details of your derivation. Calculate the variance of $\hat{\theta}$ and compare it to the variance of $\tilde{\theta}$.

  A statistician cannot remember the exact statement of the Rao-Blackwell theorem and calculates $\mathbb{E}\left(T \mid X_{1}\right)$ in an attempt to find an estimator of $\theta$. Comment on the suitability or otherwise of this approach, giving your reasons.

  [Hint: If $a$ and $b$ are positive integers then, for $r=0,1, \ldots, a+b,\left(\begin{array}{c}a+b \\ r\end{array}\right)=$ $\left.\sum_{j=0}^{r}\left(\begin{array}{c}a \\ j\end{array}\right)\left(\begin{array}{c}b \\ r-j\end{array}\right) .\right]$

  comment

• Paper 3, Section II, H

  Statistics

  Part IB, 2015

  (a) Suppose that $X_{1}, \ldots, X_{n}$ are independent identically distributed random variables, each with density $f(x)=\theta \exp (-\theta x), x>0$ for some unknown $\theta>0$. Use the generalised likelihood ratio to obtain a size $\alpha$ test of $H_{0}: \theta=1$ against $H_{1}: \theta \neq 1$.

  (b) A die is loaded so that, if $p_{i}$ is the probability of face $i$, then $p_{1}=p_{2}=\theta_{1}$, $p_{3}=p_{4}=\theta_{2}$ and $p_{5}=p_{6}=\theta_{3}$. The die is thrown $n$ times and face $i$ is observed $x_{i}$ times. Write down the likelihood function for $\theta=\left(\theta_{1}, \theta_{2}, \theta_{3}\right)$ and find the maximum likelihood estimate of $\theta$.

  Consider testing whether or not $\theta_{1}=\theta_{2}=\theta_{3}$ for this die. Find the generalised likelihood ratio statistic $\Lambda$ and show that

  $$2 \log _{e} \Lambda \approx T, \quad \text { where } T=\sum_{i=1}^{3} \frac{\left(o_{i}-e_{i}\right)^{2}}{e_{i}}$$

  where you should specify $o_{i}$ and $e_{i}$ in terms of $x_{1}, \ldots, x_{6}$. Explain how to obtain an approximate size $0.05$ test using the value of $T$. Explain what you would conclude (and why ) if $T=2.03$.

  comment

• Paper 1, Section I, A

  Variational Principles

  Part IB, 2015

  Consider a frictionless bead on a stationary wire. The bead moves under the action of gravity acting in the negative $y$-direction and the wire traces out a path $y(x)$, connecting points $(x, y)=(0,0)$ and $(1,0)$. Using a first integral of the Euler-Lagrange equations, find the choice of $y(x)$ which gives the shortest travel time, starting from rest. You may give your solution for $y$ and $x$ separately, in parametric form.

  comment

• Paper 3, Section $I$, A

  Variational Principles

  Part IB, 2015

  (a) Define what it means for a function $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$ to be convex.

  (b) Define the Legendre transform $f^{*}(p)$ of a convex function $f(x)$, where $x \in \mathbb{R}$. Show that $f^{*}(p)$ is a convex function.

  (c) Find the Legendre transform $f^{*}(p)$ of the function $f(x)=e^{x}$, and the domain of $f^{*}$.

  comment

• Paper 2, Section II, A

  Variational Principles

  Part IB, 2015

  A right circular cylinder of radius $a$ and length $l$ has volume $V$ and total surface area $A$. Use Lagrange multipliers to do the following:

  (a) Show that, for a given total surface area, the maximum volume is

  $$V=\frac{1}{3} \sqrt{\frac{A^{3}}{C \pi}}$$

  determining the integer $C$ in the process.

  (b) For a cylinder inscribed in the unit sphere, show that the value of $l / a$ which maximises the area of the cylinder is

  $$D+\sqrt{E}$$

  determining the integers $D$ and $E$ as you do so.

  (c) Consider the rectangular parallelepiped of largest volume which fits inside a hemisphere of fixed radius. Find the ratio of the parallelepiped's volume to the volume of the hemisphere.

  [You need not show that suitable extrema you find are actually maxima.]

  comment

• Paper 3, Section II, G

  Complex Analysis

  Part IB, 2015

  State the argument principle.

  Let $U \subset \mathbb{C}$ be an open set and $f: U \rightarrow \mathbb{C}$ a holomorphic injective function. Show that $f^{\prime}(z) \neq 0$ for each $z$ in $U$ and that $f(U)$ is open.

  Stating clearly any theorems that you require, show that for each $a \in U$ and a sufficiently small $r>0$,

  $$g(w)=\frac{1}{2 \pi i} \int_{|z-a|=r} \frac{z f^{\prime}(z)}{f(z)-w} d z$$

  defines a holomorphic function on some open disc $D$ about $f(a)$.

  Show that $g$ is the inverse for the restriction of $f$ to $g(D)$.

  comment

• Paper 4, Section II, A

  Variational Principles

  Part IB, 2015

  Derive the Euler-Lagrange equation for the integral

  $$\int_{x_{0}}^{x_{1}} f\left(x, u, u^{\prime}\right) d x$$

  where $u\left(x_{0}\right)$ is allowed to float, $\partial f /\left.\partial u^{\prime}\right|_{x_{0}}=0$ and $u\left(x_{1}\right)$ takes a given value.

  Given that $y(0)$ is finite, $y(1)=1$ and $y^{\prime}(1)=1$, find the stationary value of

  $$J=\int_{0}^{1}\left(x^{4}\left(y^{\prime \prime}\right)^{2}+4 x^{2}\left(y^{\prime}\right)^{2}\right) d x$$

  comment

• Paper 1, Section I, B

  Complex Analysis or Complex Methods

  Part IB, 2015

  Consider the analytic (holomorphic) functions $f$ and $g$ on a nonempty domain $\Omega$ where $g$ is nowhere zero. Prove that if $|f(z)|=|g(z)|$ for all $z$ in $\Omega$ then there exists a real constant $\alpha$ such that $f(z)=e^{i \alpha} g(z)$ for all $z$ in $\Omega$.

  comment