Consider a particle moving between the vertices of the graph below, taking steps along the edges. Let $X_{n}$ be the position of the particle at time $n$. At time $n+1$ the particle moves to one of the vertices adjoining $X_{n}$, with each of the adjoining vertices being equally likely, independently of previous moves. Explain briefly why $\left(X_{n} ; n \geqslant 0\right)$ is a Markov chain on the vertices. Is this chain irreducible? Find an invariant distribution for this chain.

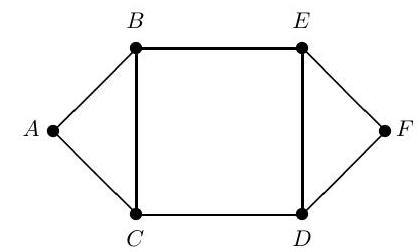
Suppose that the particle starts at $B$. By adapting the transition matrix, or otherwise, find the probability that the particle hits vertex $A$ before vertex $F$.

Find the expected first passage time from $B$ to $F$ given no intermediate visit to $A$.

[Results from the course may be used without proof provided that they are clearly stated.]