Part IB 2016

• Paper 3, Section I, G

  Analysis II

  Part IB, 2016

  (a) Let $X$ be a subset of $\mathbb{R}$. What does it mean to say that a sequence of functions $f_{n}: X \rightarrow \mathbb{R}(n \in \mathbb{N})$ is uniformly convergent?

  (b) Which of the following sequences of functions are uniformly convergent? Justify your answers.

  (i) $f_{n}:(0,1) \rightarrow \mathbb{R}, \quad f_{n}(x)=\frac{1-x^{n}}{1-x}$

  (ii) $f_{n}:(0,1) \rightarrow \mathbb{R}, \quad f_{n}(x)=\sum_{k=1}^{n} \frac{1}{k^{2}} x^{k}$.

  (iii) $f_{n}: \mathbb{R} \rightarrow \mathbb{R}$, $\quad f_{n}(x)=x / n$.

  (iv) $f_{n}:[0, \infty) \rightarrow \mathbb{R}, \quad f_{n}(x)=x e^{-n x}$.

  comment

• Paper 4, Section I, G

  Analysis II

  Part IB, 2016

  (a) What does it mean to say that a mapping $f: X \rightarrow X$ from a metric space to itself is a contraction?

  (b) State carefully the contraction mapping theorem.

  (c) Let $\left(a_{1}, a_{2}, a_{3}\right) \in \mathbb{R}^{3}$. By considering the metric space $\left(\mathbb{R}^{3}, d\right)$ with

  $$d(x, y)=\sum_{i=1}^{3}\left|x_{i}-y_{i}\right|$$

  or otherwise, show that there exists a unique solution $\left(x_{1}, x_{2}, x_{3}\right) \in \mathbb{R}^{3}$ of the system of equations

  $$\begin{aligned} &x_{1}=a_{1}+\frac{1}{6}\left(\sin x_{2}+\sin x_{3}\right), \\ &x_{2}=a_{2}+\frac{1}{6}\left(\sin x_{1}+\sin x_{3}\right), \\ &x_{3}=a_{3}+\frac{1}{6}\left(\sin x_{1}+\sin x_{2}\right) . \end{aligned}$$

  comment

• Paper 2, Section II, A

  Complex Analysis or Complex Methods

  Part IB, 2016

  Let $a=N+1 / 2$ for a positive integer $N$. Let $C_{N}$ be the anticlockwise contour defined by the square with its four vertices at $a \pm i a$ and $-a \pm i a$. Let

  $$I_{N}=\oint_{C_{N}} \frac{d z}{z^{2} \sin (\pi z)}$$

  Show that $1 / \sin (\pi z)$ is uniformly bounded on the contours $C_{N}$ as $N \rightarrow \infty$, and hence that $I_{N} \rightarrow 0$ as $N \rightarrow \infty$.

  Using this result, establish that

  $$\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}=\frac{\pi^{2}}{12}$$

  comment

• Paper 1, Section II, A

  Complex Analysis or Complex Methods

  Part IB, 2016

  Let $w=u+i v$ and let $z=x+i y$, for $u, v, x, y$ real.

  (a) Let A be the map defined by $w=\sqrt{z}$, using the principal branch. Show that A maps the region to the left of the parabola $y^{2}=4(1-x)$ on the $z-$ plane, with the negative real axis $x \in(-\infty, 0]$ removed, into the vertical strip of the $w-$ plane between the lines $u=0$ and $u=1$.

  (b) Let $\mathrm{B}$ be the map defined by $w=\tan ^{2}(z / 2)$. Show that $\mathrm{B}$ maps the vertical strip of the $z$-plane between the lines $x=0$ and $x=\pi / 2$ into the region inside the unit circle on the $w$-plane, with the part $u \in(-1,0]$ of the negative real axis removed.

  (c) Using the results of parts (a) and (b), show that the map C, defined by $w=\tan ^{2}(\pi \sqrt{z} / 4)$, maps the region to the left of the parabola $y^{2}=4(1-x)$ on the $z$-plane, including the negative real axis, onto the unit disc on the $w$-plane.

  comment

• Paper 3, Section I, A

  Complex Methods

  Part IB, 2016

  The function $f(x)$ has Fourier transform

  $$\tilde{f}(k)=\int_{-\infty}^{\infty} f(x) e^{-i k x} d x=\frac{-2 k i}{p^{2}+k^{2}},$$

  where $p>0$ is a real constant. Using contour integration, calculate $f(x)$ for $x<0$. [Jordan's lemma and the residue theorem may be used without proof.]

  comment

• Paper 4, Section II, A

  Complex Methods

  Part IB, 2016

  (a) Show that the Laplace transform of the Heaviside step function $H(t-a)$ is

  $$\int_{0}^{\infty} H(t-a) e^{-p t} d t=\frac{e^{-a p}}{p}$$

  for $a>0$.

  (b) Derive an expression for the Laplace transform of the second derivative of a function $f(t)$ in terms of the Laplace transform of $f(t)$ and the properties of $f(t)$ at $t=0$.

  (c) A bar of length $L$ has its end at $x=L$ fixed. The bar is initially at rest and straight. The end at $x=0$ is given a small fixed transverse displacement of magnitude $a$ at $t=0^{+}$. You may assume that the transverse displacement $y(x, t)$ of the bar satisfies the wave equation with some wave speed $c$, and so the tranverse displacement $y(x, t)$ is the solution to the problem:

  $$\begin{array}{cl} \frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}} & \text { for } 0<x<L \text { and } t> \\ y(x, 0)=\frac{\partial y}{\partial t}(x, 0)=0 & \text { for } 0<x<L, \\ y(0, t)=a ; y(L, t)=0 & \text { for } t>0 . \end{array}$$

  (i) Show that the Laplace transform $Y(x, p)$ of $y(x, t)$, defined as

  $$Y(x, p)=\int_{0}^{\infty} y(x, t) e^{-p t} d t$$

  is given by

  $$Y(x, p)=\frac{a \sinh \left[\frac{p}{c}(L-x)\right]}{p \sinh \left[\frac{p L}{c}\right]}$$

  (ii) By use of the binomial theorem or otherwise, express $y(x, t)$ as an infinite series.

  (iii) Plot the transverse displacement of the midpoint of the bar $y(L / 2, t)$ against time.

  comment

• Paper 2, Section I, $6 \mathrm{D}$

  Electromagnetism

  Part IB, 2016

  (a) Derive the integral form of Ampère's law from the differential form of Maxwell's equations with a time-independent magnetic field, $\rho=0$ and $\mathbf{E}=\mathbf{0}$.

  (b) Consider two perfectly-conducting concentric thin cylindrical shells of infinite length with axes along the $z$-axis and radii $a$ and $b(a<b)$. Current $I$ flows in the positive $z$-direction in each shell. Use Ampère's law to calculate the magnetic field in the three regions: (i) $r<a$, (ii) $a<r<b$ and (iii) $r>b$, where $r=\sqrt{x^{2}+y^{2}}$.

  (c) If current $I$ now flows in the positive $z$-direction in the inner shell and in the negative $z$-direction in the outer shell, calculate the magnetic field in the same three regions.

  comment

• Paper 4, Section I, D

  Electromagnetism

  Part IB, 2016

  (a) Starting from Maxwell's equations, show that in a vacuum,

  $$\frac{1}{c^{2}} \frac{\partial^{2} \mathbf{E}}{\partial t^{2}}-\nabla^{2} \mathbf{E}=\mathbf{0} \quad \text { and } \quad \boldsymbol{\nabla} \cdot \mathbf{E}=0 \quad \text { where } \quad c=\sqrt{\frac{1}{\epsilon_{0} \mu_{0}}} .$$

  (b) Suppose that $\mathbf{E}=\frac{E_{0}}{\sqrt{2}}(1,1,0) \cos (k z-\omega t)$ where $E_{0}, k$ and $\omega$ are real constants.

  (i) What are the wavevector and the polarisation? How is $\omega$ related to $k$ ?

  (ii) Find the magnetic field $\mathbf{B}$.

  (iii) Compute and interpret the time-averaged value of the Poynting vector, $\mathbf{S}=\frac{1}{\mu_{0}} \mathbf{E} \times \mathbf{B}$.

  comment

• Paper 1, Section II, D

  Electromagnetism

  Part IB, 2016

  (a) From the differential form of Maxwell's equations with $\mathbf{J}=\mathbf{0}, \mathbf{B}=\mathbf{0}$ and a time-independent electric field, derive the integral form of Gauss's law.

  (b) Derive an expression for the electric field $\mathbf{E}$ around an infinitely long line charge lying along the $z$-axis with charge per unit length $\mu$. Find the electrostatic potential $\phi$ up to an arbitrary constant.

  (c) Now consider the line charge with an ideal earthed conductor filling the region $x>d$. State the boundary conditions satisfied by $\phi$ and $\mathbf{E}$ on the surface of the conductor.

  (d) Show that the same boundary conditions at $x=d$ are satisfied if the conductor is replaced by a second line charge at $x=2 d, y=0$ with charge per unit length $-\mu$.

  (e) Hence or otherwise, returning to the setup in (c), calculate the force per unit length acting on the line charge.

  (f) What is the charge per unit area $\sigma(y, z)$ on the surface of the conductor?

  comment

• Paper 3, Section II, D

  Electromagnetism

  Part IB, 2016

  (a) State Faraday's law of induction for a moving circuit in a time-dependent magnetic field and define all the terms that appear.

  (b) Consider a rectangular circuit DEFG in the $z=0$ plane as shown in the diagram below. There are two rails parallel to the $x$-axis for $x>0$ starting at $\mathrm{D}$ at $(x, y)=(0,0)$ and $G$ at $(0, L)$. A battery provides an electromotive force $\mathcal{E}_{0}$ between $D$ and $G$ driving current in a positive sense around DEFG. The circuit is completed with a bar resistor of resistance $R$, length $L$ and mass $m$ that slides without friction on the rails; it connects $E$ at $(s(t), 0)$ and $F$ at $(s(t), L)$. The rest of the circuit has no resistance. The circuit is in a constant uniform magnetic field $B_{0}$ parallel to the $z$-axis.

  [In parts (i)-(iv) you can neglect any magnetic field due to current flow.]

  

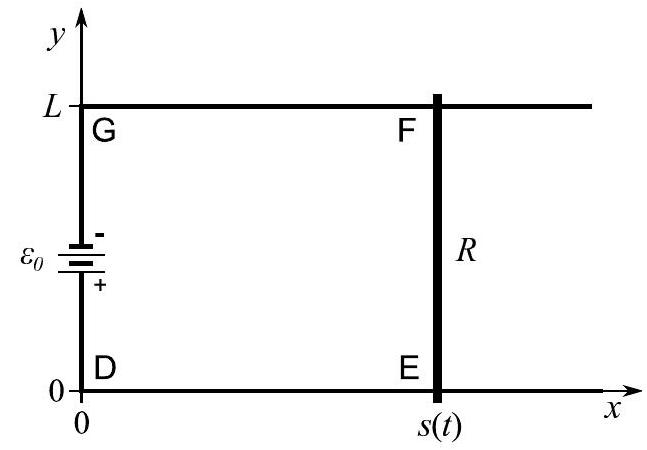
  (i) Calculate the current in the bar and indicate its direction on a diagram of the circuit.

  (ii) Find the force acting on the bar.

  (iii) If the initial velocity and position of the bar are respectively $\dot{s}(0)=v_{0}>0$ and $s(0)=s_{0}>0$, calculate $\dot{s}(t)$ and $s(t)$ for $t>0$.

  (iv) If $\mathcal{E}_{0}=0$, find the total energy dissipated in the circuit after $t=0$ and verify that total energy is conserved.

  (v) Describe qualitatively the effect of the magnetic field caused by the induced current flowing in the circuit when $\mathcal{E}_{0}=0$.

  comment

• Paper 2, Section II, D

  Electromagnetism

  Part IB, 2016

  (a) State the covariant form of Maxwell's equations and define all the quantities that appear in these expressions.

  (b) Show that $\mathbf{E} \cdot \mathbf{B}$ is a Lorentz scalar (invariant under Lorentz transformations) and find another Lorentz scalar involving $\mathbf{E}$ and $\mathbf{B}$.

  (c) In some inertial frame $S$ the electric and magnetic fields are respectively $\mathbf{E}=\left(0, E_{y}, E_{z}\right)$ and $\mathbf{B}=\left(0, B_{y}, B_{z}\right)$. Find the electric and magnetic fields, $\mathbf{E}^{\prime}=\left(0, E_{y}^{\prime}, E_{z}^{\prime}\right)$ and $\mathbf{B}^{\prime}=\left(0, B_{y}^{\prime}, B_{z}^{\prime}\right)$, in another inertial frame $S^{\prime}$ that is related to $S$ by the Lorentz transformation,

  $$\Lambda_{\nu}^{\mu}=\left(\begin{array}{cccc} \gamma & -\gamma v / c & 0 & 0 \\ -\gamma v / c & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

  where $v$ is the velocity of $S^{\prime}$ in $S$ and $\gamma=\left(1-v^{2} / c^{2}\right)^{-1 / 2}$.

  (d) Suppose that $\mathbf{E}=E_{0}(0,1,0)$ and $\mathbf{B}=\frac{E_{0}}{c}(0, \cos \theta, \sin \theta)$ where $0 \leqslant \theta \leqslant \pi / 2$, and $E_{0}$ is a real constant. An observer is moving in $S$ with velocity $v$ parallel to the $x$-axis. What must $v$ be for the electric and magnetic fields to appear to the observer to be parallel? Comment on the case $\theta=\pi / 2$.

  comment

• Paper 1, Section I, C

  Fluid Dynamics

  Part IB, 2016

  Consider the flow field in cartesian coordinates $(x, y, z)$ given by

  $$\mathbf{u}=\left(-\frac{A y}{x^{2}+y^{2}}, \frac{A x}{x^{2}+y^{2}}, U(z)\right)$$

  where $A$ is a constant. Let $\mathcal{D}$ denote the whole of $\mathbb{R}^{3}$ excluding the $z$ axis.

  (a) Determine the conditions on $A$ and $U(z)$ for the flow to be both incompressible and irrotational in $\mathcal{D}$.

  (b) Calculate the circulation along any closed curve enclosing the $z$ axis.

  comment

• Paper 2, Section I, G

  Analysis II

  Part IB, 2016

  (a) What does it mean to say that the function $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ is differentiable at the point $x=\left(x_{1}, x_{2}, \ldots, x_{n}\right) \in \mathbb{R}^{n}$ ? Show from your definition that if $f$ is differentiable at $x$, then $f$ is continuous at $x$.

  (b) Suppose that there are functions $g_{j}: \mathbb{R} \rightarrow \mathbb{R}^{m}(1 \leqslant j \leqslant n)$ such that for every $x=\left(x_{1}, \ldots, x_{n}\right) \in \mathbb{R}^{n}$,

  $$f(x)=\sum_{j=1}^{n} g_{j}\left(x_{j}\right) .$$

  Show that $f$ is differentiable at $x$ if and only if each $g_{j}$ is differentiable at $x_{j}$.

  (c) Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be given by

  $$f(x, y)=|x|^{3 / 2}+|y|^{1 / 2}$$

  Determine at which points $(x, y) \in \mathbb{R}^{2}$ the function $f$ is differentiable.

  comment

• Paper 2, Section I, C

  Fluid Dynamics

  Part IB, 2016

  A steady, two-dimensional unidirectional flow of a fluid with dynamic viscosity $\mu$ is set up between two plates at $y=0$ and $y=h$. The plate at $y=0$ is stationary while the plate at $y=h$ moves with constant speed $U \mathbf{e}_{x}$. The fluid is also subject to a constant pressure gradient $-G \mathbf{e}_{x}$. You may assume that the fluid velocity $\mathbf{u}$ has the form $\mathbf{u}=u(y) \mathbf{e}_{x}$.

  (a) State the equation satisfied by $u(y)$ and its boundary conditions.

  (b) Calculate $u(y)$.

  (c) Show that the value of $U$ may be chosen to lead to zero viscous shear stress acting on the bottom plate and calculate the resulting flow rate.

  comment

• Paper 1, Section II, $17 \mathrm{C}$

  Fluid Dynamics

  Part IB, 2016

  (a) For a velocity field $\mathbf{u}$, show that $\mathbf{u} \cdot \boldsymbol{\nabla} \mathbf{u}=\boldsymbol{\nabla}\left(\frac{1}{2} \mathbf{u}^{2}\right)-\mathbf{u} \times \boldsymbol{\omega}$, where $\boldsymbol{\omega}$ is the flow vorticity.

  (b) For a scalar field $H(\mathbf{r})$, show that if $\mathbf{u} \cdot \nabla H=0$, then $H$ is constant along the flow streamlines.

  (c) State the Euler equations satisfied by an inviscid fluid of constant density subject to conservative body forces.

  (i) If the flow is irrotational, show that an exact first integral of the Euler equations may be obtained.

  (ii) If the flow is not irrotational, show that although an exact first integral of the Euler equations may not be obtained, a similar quantity is constant along the flow streamlines provided the flow is steady.

  (iii) If the flow is now in a frame rotating with steady angular velocity $\Omega \mathbf{e}_{z}$, establish that a similar quantity is constant along the flow streamlines with an extra term due to the centrifugal force when the flow is steady.

  comment

• Paper 4, Section II, C

  Fluid Dynamics

  Part IB, 2016

  (a) Show that for an incompressible fluid, $\nabla \times \boldsymbol{\omega}=-\nabla^{2} \mathbf{u}$, where $\boldsymbol{\omega}$ is the flow vorticity,

  (b) State the equation of motion for an inviscid flow of constant density in a rotating frame subject to gravity. Show that, on Earth, the local vertical component of the centrifugal force is small compared to gravity. Present a scaling argument to justify the linearisation of the Euler equations for sufficiently large rotation rates, and hence deduce the linearised version of the Euler equations in a rapidly rotating frame.

  (c) Denoting the rotation rate of the frame as $\boldsymbol{\Omega}=\Omega \mathbf{e}_{z}$, show that the linearised Euler equations may be manipulated to obtain an equation for the velocity field $\mathbf{u}$ in the form

  $$\frac{\partial^{2} \nabla^{2} \mathbf{u}}{\partial t^{2}}+4 \Omega^{2} \frac{\partial^{2} \mathbf{u}}{\partial z^{2}}=\mathbf{0}$$

  (d) Assume that there exist solutions of the form $\mathbf{u}=\mathbf{U}_{0} \exp [i(\mathbf{k} \cdot \mathbf{x}-\omega t)]$. Show that $\omega=\pm 2 \Omega \cos \theta$ where the angle $\theta$ is to be determined.

  comment

• Paper 3, Section II, C

  Fluid Dynamics

  Part IB, 2016

  A layer of thickness $h_{1}$ of a fluid of density $\rho_{1}$ is located above a layer of thickness $h_{2}$ of a fluid of density $\rho_{2}>\rho_{1}$. The two-fluid system is bounded by two impenetrable surfaces at $y=h_{1}$ and $y=-h_{2}$ and is assumed to be two-dimensional (i.e. independent of $z$ ). The fluid is subsequently perturbed, and the interface between the two fluids is denoted $y=\eta(x, t)$.

  (a) Assuming irrotational motion in each fluid, state the equations and boundary conditions satisfied by the flow potentials, $\varphi_{1}$ and $\varphi_{2}$.

  (b) The interface is perturbed by small-amplitude waves of the form $\eta=\eta_{0} e^{i(k x-\omega t)}$, with $\eta_{0} k \ll 1$. State the equations and boundary conditions satisfied by the linearised system.

  (c) Calculate the dispersion relation of the waves relating the frequency $\omega$ to the wavenumber $k$.

  comment

• Paper 1, Section I, F

  Geometry

  Part IB, 2016

  (a) Describe the Poincaré disc model $D$ for the hyperbolic plane by giving the appropriate Riemannian metric.

  (b) Let $a \in D$ be some point. Write down an isometry $f: D \rightarrow D$ with $f(a)=0$.

  (c) Using the Poincaré disc model, calculate the distance from 0 to re $e^{i \theta}$ with $0 \leqslant r<1$

  (d) Using the Poincaré disc model, calculate the area of a disc centred at a point $a \in D$ and of hyperbolic radius $\rho>0$.

  comment

• Paper 3, Section I, $5 F$

  Geometry

  Part IB, 2016

  (a) State Euler's formula for a triangulation of a sphere.

  (b) A sphere is decomposed into hexagons and pentagons with precisely three edges at each vertex. Determine the number of pentagons.

  comment

• Paper 3, Section II, F

  Geometry

  Part IB, 2016

  (a) Define the cross-ratio $\left[z_{1}, z_{2}, z_{3}, z_{4}\right]$ of four distinct points $z_{1}, z_{2}, z_{3}, z_{4} \in \mathbb{C} \cup\{\infty\}$. Show that the cross-ratio is invariant under Möbius transformations. Express $\left[z_{2}, z_{1}, z_{3}, z_{4}\right]$ in terms of $\left[z_{1}, z_{2}, z_{3}, z_{4}\right]$.

  (b) Show that $\left[z_{1}, z_{2}, z_{3}, z_{4}\right]$ is real if and only if $z_{1}, z_{2}, z_{3}, z_{4}$ lie on a line or circle in $\mathbb{C} \cup\{\infty\}$.

  (c) Let $z_{1}, z_{2}, z_{3}, z_{4}$ lie on a circle in $\mathbb{C}$, given in anti-clockwise order as depicted.

  

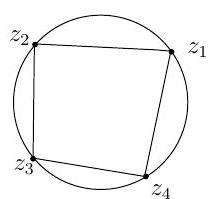
  Show that $\left[z_{1}, z_{2}, z_{3}, z_{4}\right]$ is a negative real number, and that $\left[z_{2}, z_{1}, z_{3}, z_{4}\right]$ is a positive real number greater than 1 . Show that $\left|\left[z_{1}, z_{2}, z_{3}, z_{4}\right]\right|+1=\left|\left[z_{2}, z_{1}, z_{3}, z_{4}\right]\right|$. Use this to deduce Ptolemy's relation on lengths of edges and diagonals of the inscribed 4-gon:

  $$\left|z_{1}-z_{3}\right|\left|z_{2}-z_{4}\right|=\left|z_{1}-z_{2}\right|\left|z_{3}-z_{4}\right|+\left|z_{2}-z_{3}\right|\left|z_{4}-z_{1}\right|$$

  comment

• Paper 2, Section II, F

  Geometry

  Part IB, 2016

  (a) Let $A B C$ be a hyperbolic triangle, with the angle at $A$ at least $\pi / 2$. Show that the side $B C$ has maximal length amongst the three sides of $A B C$.

  [You may use the hyperbolic cosine formula without proof. This states that if $a, b$ and $c$ are the lengths of $B C, A C$, and $A B$ respectively, and $\alpha, \beta$ and $\gamma$ are the angles of the triangle at $A, B$ and $C$ respectively, then

  $$\cosh a=\cosh b \cosh c-\sinh b \sinh c \cos \alpha .]$$

  (b) Given points $z_{1}, z_{2}$ in the hyperbolic plane, let $w$ be any point on the hyperbolic line segment joining $z_{1}$ to $z_{2}$, and let $w^{\prime}$ be any point not on the hyperbolic line passing through $z_{1}, z_{2}, w$. Show that

  $$\rho\left(w^{\prime}, w\right) \leqslant \max \left\{\rho\left(w^{\prime}, z_{1}\right), \rho\left(w^{\prime}, z_{2}\right)\right\}$$

  where $\rho$ denotes hyperbolic distance.

  (c) The diameter of a hyperbolic triangle $\Delta$ is defined to be

  $$\sup \{\rho(P, Q) \mid P, Q \in \Delta\}$$

  Show that the diameter of $\Delta$ is equal to the length of its longest side.

  comment

• Paper 4, Section II, F

  Geometry

  Part IB, 2016

  Let $\alpha(s)=(f(s), g(s))$ be a simple curve in $\mathbb{R}^{2}$ parameterised by arc length with $f(s)>0$ for all $s$, and consider the surface of revolution $S$ in $\mathbb{R}^{3}$ defined by the parameterisation

  $$\sigma(u, v)=(f(u) \cos v, f(u) \sin v, g(u))$$

  (a) Calculate the first and second fundamental forms for $S$. Show that the Gaussian curvature of $S$ is given by

  $$K=-\frac{f^{\prime \prime}(u)}{f(u)}$$

  (b) Now take $f(s)=\cos s+2, g(s)=\sin s, 0 \leqslant s<2 \pi$. What is the integral of the Gaussian curvature over the surface of revolution $S$ determined by $f$ and $g$ ?

  [You may use the Gauss-Bonnet theorem without proof.]

  (c) Now suppose $S$ has constant curvature $K \equiv 1$, and suppose there are two points $P_{1}, P_{2} \in \mathbb{R}^{3}$ such that $S \cup\left\{P_{1}, P_{2}\right\}$ is a smooth closed embedded surface. Show that $S$ is a unit sphere, minus two antipodal points.

  [Do not attempt to integrate an expression of the form $\sqrt{1-C^{2} \sin ^{2} u}$ when $C \neq 1$. Study the behaviour of the surface at the largest and smallest possible values of $u$.]

  comment

• Paper 3, Section I, E

  Groups, Rings and Modules

  Part IB, 2016

  Let $G$ be a group of order $n$. Define what is meant by a permutation representation of $G$. Using such representations, show $G$ is isomorphic to a subgroup of the symmetric group $S_{n}$. Assuming $G$ is non-abelian simple, show $G$ is isomorphic to a subgroup of $A_{n}$. Give an example of a permutation representation of $S_{3}$ whose kernel is $A_{3}$.

  comment

• Paper 1, Section II, G

  Analysis II

  Part IB, 2016

  Let $(X, d)$ be a metric space.

  (a) What does it mean to say that $\left(x_{n}\right)_{n}$ is a Cauchy sequence in $X$ ? Show that if $\left(x_{n}\right)_{n}$ is a Cauchy sequence, then it converges if it contains a convergent subsequence.

  (b) Let $\left(x_{n}\right)_{n}$ be a Cauchy sequence in $X$.

  (i) Show that for every $m \geqslant 1$, the sequence $\left(d\left(x_{m}, x_{n}\right)\right)_{n}$ converges to some $d_{m} \in \mathbb{R}$.

  (ii) Show that $d_{m} \rightarrow 0$ as $m \rightarrow \infty$.

  (iii) Let $\left(y_{n}\right)_{n}$ be a subsequence of $\left(x_{n}\right)_{n}$. If $\ell, m$ are such that $y_{\ell}=x_{m}$, show that $d\left(y_{\ell}, y_{n}\right) \rightarrow d_{m}$ as $n \rightarrow \infty$.

  (iv) Show also that for every $m$ and $n$,

  $$d_{m}-d_{n} \leqslant d\left(x_{m}, x_{n}\right) \leqslant d_{m}+d_{n}$$

  (v) Deduce that $\left(x_{n}\right)_{n}$ has a subsequence $\left(y_{n}\right)_{n}$ such that for every $m$ and $n$,

  $$d\left(y_{m+1}, y_{m}\right) \leqslant \frac{1}{3} d\left(y_{m}, y_{m-1}\right)$$

  and

  $$d\left(y_{m+1}, y_{n+1}\right) \leqslant \frac{1}{2} d\left(y_{m}, y_{n}\right)$$

  (c) Suppose that every closed subset $Y$ of $X$ has the property that every contraction mapping $Y \rightarrow Y$ has a fixed point. Prove that $X$ is complete.

  comment

• Paper 4, Section I, $2 \mathrm{E}$

  Groups, Rings and Modules

  Part IB, 2016

  Give the statement and the proof of Eisenstein's criterion. Use this criterion to show $x^{p-1}+x^{p-2}+\cdots+1$ is irreducible in $\mathbb{Q}[x]$ where $p$ is a prime.

  comment

• Paper 2, Section I, E

  Groups, Rings and Modules

  Part IB, 2016

  Let $R$ be an integral domain.

  Define what is meant by the field of fractions $F$ of $R$. [You do not need to prove the existence of $F$.]

  Suppose that $\phi: R \rightarrow K$ is an injective ring homomorphism from $R$ to a field $K$. Show that $\phi$ extends to an injective ring homomorphism $\Phi: F \rightarrow K$.

  Give an example of $R$ and a ring homomorphism $\psi: R \rightarrow S$ from $R$ to a ring $S$ such that $\psi$ does not extend to a ring homomorphism $F \rightarrow S$.

  comment

• Paper 1, Section II, E

  Groups, Rings and Modules

  Part IB, 2016

  (a) Let $I$ be an ideal of a commutative ring $R$ and assume $I \subseteq \bigcup_{i=1}^{n} P_{i}$ where the $P_{i}$ are prime ideals. Show that $I \subseteq P_{i}$ for some $i$.

  (b) Show that $\left(x^{2}+1\right)$ is a maximal ideal of $\mathbb{R}[x]$. Show that the quotient ring $\mathbb{R}[x] /\left(x^{2}+1\right)$ is isomorphic to $\mathbb{C} .$

  (c) For $a, b \in \mathbb{R}$, let $I_{a, b}$ be the ideal $(x-a, y-b)$ in $\mathbb{R}[x, y]$. Show that $I_{a, b}$ is a maximal ideal. Find a maximal ideal $J$ of $\mathbb{R}[x, y]$ such that $J \neq I_{a, b}$ for any $a, b \in \mathbb{R}$. Justify your answers.

  comment

• Paper 3, Section II, E

  Groups, Rings and Modules

  Part IB, 2016

  (a) Define what is meant by an algebraic integer $\alpha$. Show that the ideal

  $$I=\{h \in \mathbb{Z}[x] \mid h(\alpha)=0\}$$

  in $\mathbb{Z}[x]$ is generated by a monic irreducible polynomial $f$. Show that $\mathbb{Z}[\alpha]$, considered as a $\mathbb{Z}$-module, is freely generated by $n$ elements where $n=\operatorname{deg} f$.

  (b) Assume $\alpha \in \mathbb{C}$ satisfies $\alpha^{5}+2 \alpha+2=0$. Is it true that the ideal (5) in $\mathbb{Z}[\alpha]$ is a prime ideal? Is there a ring homomorphism $\mathbb{Z}[\alpha] \rightarrow \mathbb{Z}[\sqrt{-1}]$ ? Justify your answers.

  (c) Show that the only unit elements of $\mathbb{Z}[\sqrt{-5}]$ are 1 and $-1$. Show that $\mathbb{Z}[\sqrt{-5}]$ is not a UFD.

  comment

• Paper 4, Section II, E

  Groups, Rings and Modules

  Part IB, 2016

  Let $R$ be a Noetherian ring and let $M$ be a finitely generated $R$-module.

  (a) Show that every submodule of $M$ is finitely generated.

  (b) Show that each maximal element of the set

  $$\mathcal{A}=\{\operatorname{Ann}(m) \mid 0 \neq m \in M\}$$

  is a prime ideal. [Here, maximal means maximal with respect to inclusion, and $\operatorname{Ann}(m)=\{r \in R \mid r m=0\} .]$

  (c) Show that there is a chain of submodules

  $$0=M_{0} \subseteq M_{1} \subseteq \cdots \subseteq M_{l}=M$$

  such that for each $0<i \leqslant l$ the quotient $M_{i} / M_{i-1}$ is isomorphic to $R / P_{i}$ for some prime ideal $P_{i}$.

  comment

• Paper 2, Section II, E

  Groups, Rings and Modules

  Part IB, 2016

  (a) State Sylow's theorems and give the proof of the second theorem which concerns conjugate subgroups.

  (b) Show that there is no simple group of order 351 .

  (c) Let $k$ be the finite field $\mathbb{Z} /(31)$ and let $G L_{2}(k)$ be the multiplicative group of invertible $2 \times 2$ matrices over $k$. Show that every Sylow 3-subgroup of $G L_{2}(k)$ is abelian.

  comment

• Paper 4, Section I, F

  Linear Algebra

  Part IB, 2016

  For which real numbers $x$ do the vectors

  $$(x, 1,1,1), \quad(1, x, 1,1), \quad(1,1, x, 1), \quad(1,1,1, x),$$

  not form a basis of $\mathbb{R}^{4}$ ? For each such value of $x$, what is the dimension of the subspace of $\mathbb{R}^{4}$ that they span? For each such value of $x$, provide a basis for the spanned subspace, and extend this basis to a basis of $\mathbb{R}^{4}$.

  comment

• Paper 2, Section I, F

  Linear Algebra

  Part IB, 2016

  Find a linear change of coordinates such that the quadratic form

  $$2 x^{2}+8 x y-6 x z+y^{2}-4 y z+2 z^{2}$$

  takes the form

  $$\alpha x^{2}+\beta y^{2}+\gamma z^{2}$$

  for real numbers $\alpha, \beta$ and $\gamma$.

  comment

• Paper 1, Section $I$, $1 F$

  Linear Algebra

  Part IB, 2016

  (a) Consider the linear transformation $\alpha: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$ given by the matrix

  $$\left(\begin{array}{rrr} 5 & -6 & -6 \\ -1 & 4 & 2 \\ 3 & -6 & -4 \end{array}\right)$$

  Find a basis of $\mathbb{R}^{3}$ in which $\alpha$ is represented by a diagonal matrix.

  (b) Give a list of $6 \times 6$ matrices such that any linear transformation $\beta: \mathbb{R}^{6} \rightarrow \mathbb{R}^{6}$ with characteristic polynomial

  $$(x-2)^{4}(x+7)^{2}$$

  and minimal polynomial

  $$(x-2)^{2}(x+7)$$

  is similar to one of the matrices on your list. No two distinct matrices on your list should be similar. [No proof is required.]

  comment

• Paper 1, Section II, F

  Linear Algebra

  Part IB, 2016

  Let $M_{n, n}$ denote the vector space over $F=\mathbb{R}$ or $\mathbb{C}$ of $n \times n$ matrices with entries in $F$. Let $\operatorname{Tr}: M_{n, n} \rightarrow F$ denote the trace functional, i.e., if $A=\left(a_{i j}\right)_{1 \leqslant i, j \leqslant n} \in M_{n, n}$, then

  $$\operatorname{Tr}(A)=\sum_{i=1}^{n} a_{i i}$$

  (a) Show that Tr is a linear functional.

  (b) Show that $\operatorname{Tr}(A B)=\operatorname{Tr}(B A)$ for $A, B \in M_{n, n}$.

  (c) Show that $\operatorname{Tr}$ is unique in the following sense: If $f: M_{n, n} \rightarrow F$ is a linear functional such that $f(A B)=f(B A)$ for each $A, B \in M_{n, n}$, then $f$ is a scalar multiple of the trace functional. If, in addition, $f(I)=n$, then $f=$ Tr.

  (d) Let $W \subseteq M_{n, n}$ be the subspace spanned by matrices $C$ of the form $C=A B-B A$ for $A, B \in M_{n, n}$. Show that $W$ is the kernel of Tr.

  comment

• Paper 4, Section II, G

  Analysis II

  Part IB, 2016

  (a) Let $V$ be a real vector space. What does it mean to say that two norms on $V$ are Lipschitz equivalent? Prove that every norm on $\mathbb{R}^{n}$ is Lipschitz equivalent to the Euclidean norm. Hence or otherwise, show that any linear map from $\mathbb{R}^{n}$ to $\mathbb{R}^{m}$ is continuous.

  (b) Let $f: U \rightarrow V$ be a linear map between normed real vector spaces. We say that $f$ is bounded if there exists a constant $C$ such that for all $u \in U,\|f(u)\| \leqslant C\|u\|$. Show that $f$ is bounded if and only if $f$ is continuous.

  (c) Let $\ell^{2}$ denote the space of sequences $\left(x_{n}\right)_{n \geqslant 1}$ of real numbers such that $\sum_{n \geqslant 1} x_{n}^{2}$ is convergent, with the norm $\left\|\left(x_{n}\right)_{n}\right\|=\left(\sum_{n \geqslant 1} x_{n}^{2}\right)^{1 / 2}$. Let $e_{m} \in \ell^{2}$ be the sequence $e_{m}=\left(x_{n}\right)_{n}$ with $x_{m}=1$ and $x_{n}=0$ if $n \neq m$. Let $w$ be the sequence $\left(2^{-n}\right)_{n}$. Show that the subset $\{w\} \cup\left\{e_{m} \mid m \geqslant 1\right\}$ is linearly independent. Let $V \subset \ell^{2}$ be the subspace it spans, and consider the linear map $f: V \rightarrow \mathbb{R}$ defined by

  $$f(w)=1, \quad f\left(e_{m}\right)=0 \quad \text { for all } m \geqslant 1 .$$

  Is $f$ continuous? Justify your answer.

  comment

• Paper 4, Section II, F

  Linear Algebra

  Part IB, 2016

  (a) Let $\alpha: V \rightarrow W$ be a linear transformation between finite dimensional vector spaces over a field $F=\mathbb{R}$ or $\mathbb{C}$.

  Define the dual map of $\alpha$. Let $\delta$ be the dual map of $\alpha$. Given a subspace $U \subseteq V$, define the annihilator $U^{\circ}$ of $U$. Show that $(\operatorname{ker} \alpha)^{\circ}$ and the image of $\delta$ coincide. Conclude that the dimension of the image of $\alpha$ is equal to the dimension of the image of $\delta$. Show that $\operatorname{dim} \operatorname{ker}(\alpha)-\operatorname{dim} \operatorname{ker}(\delta)=\operatorname{dim} V-\operatorname{dim} W$.

  (b) Now suppose in addition that $V, W$ are inner product spaces. Define the adjoint $\alpha^{*}$ of $\alpha$. Let $\beta: U \rightarrow V, \gamma: V \rightarrow W$ be linear transformations between finite dimensional inner product spaces. Suppose that the image of $\beta$ is equal to the kernel of $\gamma$. Then show that $\beta \beta^{*}+\gamma^{*} \gamma$ is an isomorphism.

  comment

• Paper 3, Section II, F

  Linear Algebra

  Part IB, 2016

  Let $\alpha: V \rightarrow V$ be a linear transformation defined on a finite dimensional inner product space $V$ over $\mathbb{C}$. Recall that $\alpha$ is normal if $\alpha$ and its adjoint $\alpha^{*}$ commute. Show that $\alpha$ being normal is equivalent to each of the following statements:

  (i) $\alpha=\alpha_{1}+i \alpha_{2}$ where $\alpha_{1}, \alpha_{2}$ are self-adjoint operators and $\alpha_{1} \alpha_{2}=\alpha_{2} \alpha_{1}$;

  (ii) there is an orthonormal basis for $V$ consisting of eigenvectors of $\alpha$;

  (iii) there is a polynomial $g$ with complex coefficients such that $\alpha^{*}=g(\alpha)$.

  comment

• Paper 2, Section II, F

  Linear Algebra

  Part IB, 2016

  Let $M_{n, n}$ denote the vector space over a field $F=\mathbb{R}$ or $\mathbb{C}$ of $n \times n$ matrices with entries in $F$. Given $B \in M_{n, n}$, consider the two linear transformations $R_{B}, L_{B}: M_{n, n} \rightarrow$ $M_{n, n}$ defined by

  $$L_{B}(A)=B A, \quad R_{B}(A)=A B$$

  (a) Show that $\operatorname{det} L_{B}=(\operatorname{det} B)^{n}$.

  [For parts (b) and (c), you may assume the analogous result $\operatorname{det} R_{B}=(\operatorname{det} B)^{n}$ without proof.]

  (b) Now let $F=\mathbb{C}$. For $B \in M_{n, n}$, write $B^{*}$ for the conjugate transpose of $B$, i.e., $B^{*}:=\bar{B}^{T}$. For $B \in M_{n, n}$, define the linear transformation $M_{B}: M_{n, n} \rightarrow M_{n, n}$ by

  $$M_{B}(A)=B A B^{*}$$

  Show that $\operatorname{det} M_{B}=|\operatorname{det} B|^{2 n}$.

  (c) Again let $F=\mathbb{C}$. Let $W \subseteq M_{n, n}$ be the set of Hermitian matrices. [Note that $W$ is not a vector space over $\mathbb{C}$ but only over $\mathbb{R} .]$ For $B \in M_{n, n}$ and $A \in W$, define $T_{B}(A)=B A B^{*}$. Show that $T_{B}$ is an $\mathbb{R}$-linear operator on $W$, and show that as such,

  $$\operatorname{det} T_{B}=|\operatorname{det} B|^{2 n}$$

  comment

• Paper 4, Section I, H

  Markov Chains

  Part IB, 2016

  Consider two boxes, labelled $\mathrm{A}$ and B. Initially, there are no balls in box $\mathrm{A}$ and $k$ balls in box B. Each minute later, one of the $k$ balls is chosen uniformly at random and is moved to the opposite box. Let $X_{n}$ denote the number of balls in box A at time $n$, so that $X_{0}=0$.

  (a) Find the transition probabilities of the Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ and show that it is reversible in equilibrium.

  (b) Find $\mathbb{E}(T)$, where $T=\inf \left\{n \geqslant 1: X_{n}=0\right\}$ is the next time that all $k$ balls are again in box $B$.

  comment

• Paper 3, Section I, H

  Markov Chains

  Part IB, 2016

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain such that $X_{0}=i$. Prove that

  $$\sum_{n=0}^{\infty} \mathbb{P}_{i}\left(X_{n}=i\right)=\frac{1}{\mathbb{P}_{i}\left(X_{n} \neq i \text { for all } n \geqslant 1\right)}$$

  where $1 / 0=+\infty$. [You may use the strong Markov property without proof.]

  comment

• Paper 2, Section II, H

  Markov Chains

  Part IB, 2016

  (a) Prove that every open communicating class of a Markov chain is transient. Prove that every finite transient communicating class is open. Give an example of a Markov chain with an infinite transient closed communicating class.

  (b) Consider a Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ with state space $\{a, b, c, d\}$ and transition probabilities given by the matrix

  $$P=\left(\begin{array}{cccc} 1 / 3 & 0 & 1 / 3 & 1 / 3 \\ 0 & 1 / 4 & 0 & 3 / 4 \\ 1 / 2 & 1 / 2 & 0 & 0 \\ 0 & 2 / 3 & 0 & 1 / 3 \end{array}\right)$$

  (i) Compute $\mathbb{P}\left(X_{n}=b \mid X_{0}=d\right)$ for a fixed $n \geqslant 0$.

  (ii) Compute $\mathbb{P}\left(X_{n}=c\right.$ for some $\left.n \geqslant 1 \mid X_{0}=a\right)$.

  (iii) Show that $P^{n}$ converges as $n \rightarrow \infty$, and determine the limit.

  [Results from lectures can be used without proof if stated carefully.]

  comment

• Paper 1, Section II, H

  Markov Chains

  Part IB, 2016

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple symmetric random walk on the integers, starting at $X_{0}=0$.

  (a) What does it mean to say that a Markov chain is irreducible? What does it mean to say that an irreducible Markov chain is recurrent? Show that $\left(X_{n}\right)_{n} \geqslant 0$ is irreducible and recurrent.

  [Hint: You may find it helpful to use the limit

  $$\lim _{k \rightarrow \infty} \sqrt{k} 2^{-2 k}\left(\begin{array}{c} 2 k \\ k \end{array}\right)=\sqrt{\pi}$$

  You may also use without proof standard necessary and sufficient conditions for recurrence.]

  (b) What does it mean to say that an irreducible Markov chain is positive recurrent? Determine, with proof, whether $\left(X_{n}\right)_{n \geqslant 0}$ is positive recurrent.

  (c) Let

  $$T=\inf \left\{n \geqslant 1: X_{n}=0\right\}$$

  be the first time the chain returns to the origin. Compute $\mathbb{E}\left[s^{T}\right]$ for a fixed number $0<s<1$.

  comment

• Paper 2, Section I, A

  Methods

  Part IB, 2016

  Use the method of characteristics to find $u(x, y)$ in the first quadrant $x \geqslant 0, y \geqslant 0$, where $u(x, y)$ satisfies

  $$\frac{\partial u}{\partial x}-2 x \frac{\partial u}{\partial y}=\cos x$$

  with boundary data $u(x, 0)=\cos x$.

  comment

• Paper 4, Section I, A

  Methods

  Part IB, 2016

  Consider the function $f(x)$ defined by

  $$f(x)=x^{2}, \text { for }-\pi<x<\pi$$

  Calculate the Fourier series representation for the $2 \pi$-periodic extension of this function. Hence establish that

  $$\frac{\pi^{2}}{6}=\sum_{n=1}^{\infty} \frac{1}{n^{2}}$$

  and that

  $$\frac{\pi^{2}}{12}=\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n^{2}}$$

  comment

• Paper 3, Section $\mathbf{I}$, A

  Methods

  Part IB, 2016

  Calculate the Green's function $G(x ; \xi)$ given by the solution to

  $$\frac{d^{2} G}{d x^{2}}=\delta(x-\xi) ; \quad G(0 ; \xi)=\frac{d G}{d x}(1 ; \xi)=0$$

  where $\xi \in(0,1), x \in(0,1)$ and $\delta(x)$ is the Dirac $\delta$-function. Use this Green's function to calculate an explicit solution $y(x)$ to the boundary value problem

  $$\frac{d^{2} y}{d x^{2}}=x e^{-x}$$

  where $x \in(0,1)$, and $y(0)=y^{\prime}(1)=0$.

  comment

• Paper 3, Section II, G

  Analysis II

  Part IB, 2016

  Let $X$ be a metric space.

  (a) What does it mean to say that a function $f: X \rightarrow \mathbb{R}$ is uniformly continuous? What does it mean to say that $f$ is Lipschitz? Show that if $f$ is Lipschitz then it is uniformly continuous. Show also that if $\left(x_{n}\right)_{n}$ is a Cauchy sequence in $X$, and $f$ is uniformly continuous, then the sequence $\left(f\left(x_{n}\right)\right)_{n}$ is convergent.

  (b) Let $f: X \rightarrow \mathbb{R}$ be continuous, and $X$ be sequentially compact. Show that $f$ is uniformly continuous. Is $f$ necessarily Lipschitz? Justify your answer.

  (c) Let $Y$ be a dense subset of $X$, and let $g: Y \rightarrow \mathbb{R}$ be a continuous function. Show that there exists at most one continuous function $f: X \rightarrow \mathbb{R}$ such that for all $y \in Y$, $f(y)=g(y)$. Prove that if $g$ is uniformly continuous, then such a function $f$ exists, and is uniformly continuous.

  [A subset $Y \subset X$ is dense if for any nonempty open subset $U \subset X$, the intersection $U \cap Y$ is nonempty.]

  comment

• Paper 1, Section II, A

  Methods

  Part IB, 2016

  (a) Consider the general self-adjoint problem for $y(x)$ on $[a, b]$ :

  $$-\frac{d}{d x}\left[p(x) \frac{d}{d x} y\right]+q(x) y=\lambda w(x) y ; \quad y(a)=y(b)=0$$

  where $\lambda$ is the eigenvalue, and $w(x)>0$. Prove that eigenfunctions associated with distinct eigenvalues are orthogonal with respect to a particular inner product which you should define carefully.

  (b) Consider the problem for $y(x)$ given by

  $$x y^{\prime \prime}+3 y^{\prime}+\left(\frac{1+\lambda}{x}\right) y=0 ; \quad y(1)=y(e)=0 .$$

  (i) Recast this problem into self-adjoint form.

  (ii) Calculate the complete set of eigenfunctions and associated eigenvalues for this problem. [Hint: You may find it useful to make the substitution $\left.x=e^{s} .\right]$

  (iii) Verify that the eigenfunctions associated with distinct eigenvalues are indeed orthogonal.

  comment

• Paper 3, Section II, B

  Methods

  Part IB, 2016

  (a) Show that the Fourier transform of $f(x)=e^{-a^{2} x^{2}}$, for $a>0$, is

  $$\tilde{f}(k)=\frac{\sqrt{\pi}}{a} e^{-\frac{k^{2}}{4 a^{2}}},$$

  stating clearly any properties of the Fourier transform that you use.

  [Hint: You may assume that $\int_{0}^{\infty} e^{-t^{2}} d t=\sqrt{\pi} / 2$.]

  (b) Consider now the Cauchy problem for the diffusion equation in one space dimension, i.e. solving for $\theta(x, t)$ satisfying:

  $$\frac{\partial \theta}{\partial t}=D \frac{\partial^{2} \theta}{\partial x^{2}} \quad \text { with } \theta(x, 0)=g(x)$$

  where $D$ is a positive constant and $g(x)$ is specified. Consider the following property of a solution:

  Property P: If the initial data $g(x)$ is positive and it is non-zero only within a bounded region (i.e. there is a constant $\alpha$ such that $\theta(x, 0)=0$ for all $|x|>\alpha)$, then for any $\epsilon>0$ (however small) and $\beta$ (however large) the solution $\theta(\beta, \epsilon)$ can be non-zero, i.e. the solution can become non-zero arbitrarily far away after an arbitrarily short time.

  Does Property P hold for solutions of the diffusion equation? Justify your answer (deriving any expression for the solution $\theta(x, t)$ that you use).

  (c) Consider now the wave equation in one space dimension:

  $$\frac{\partial^{2} u}{\partial t^{2}}=c^{2} \frac{\partial^{2} u}{\partial x^{2}}$$

  with given initial data $u(x, 0)=\phi(x)$ and $\frac{\partial u}{\partial t}(x, 0)=0$ (and $c$ is a constant).

  Does Property $\mathrm{P}$ (with $g(x)$ and $\theta(\beta, \epsilon)$ now replaced by $\phi(x)$ and $u(\beta, \epsilon)$ respectively) hold for solutions of the wave equation? Justify your answer again as above.

  comment

• Paper 2, Section II, A

  Methods

  Part IB, 2016

  Consider a bar of length $\pi$ with free ends, subject to longitudinal vibrations. You may assume that the longitudinal displacement $y(x, t)$ of the bar satisfies the wave equation with some wave speed $c$ :

  $$\frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}}$$

  for $x \in(0, \pi)$ and $t>0$ with boundary conditions:

  $$\frac{\partial y}{\partial x}(0, t)=\frac{\partial y}{\partial x}(\pi, t)=0$$

  for $t>0$. The bar is initially at rest so that

  $$\frac{\partial y}{\partial t}(x, 0)=0$$

  for $x \in(0, \pi)$, with a spatially varying initial longitudinal displacement given by

  $$y(x, 0)=b x$$

  for $x \in(0, \pi)$, where $b$ is a real constant.

  (a) Using separation of variables, show that

  $$y(x, t)=\frac{b \pi}{2}-\frac{4 b}{\pi} \sum_{n=1}^{\infty} \frac{\cos [(2 n-1) x] \cos [(2 n-1) c t]}{(2 n-1)^{2}}$$

  (b) Determine a periodic function $P(x)$ such that this solution may be expressed as

  $$y(x, t)=\frac{1}{2}[P(x+c t)+P(x-c t)]$$

  comment

• Paper 4, Section II, B

  Methods

  Part IB, 2016

  Let $\mathcal{D}$ be a 2-dimensional region in $\mathbb{R}^{2}$ with boundary $\partial \mathcal{D}$. In this question you may assume Green's second identity:

  $$\int_{\mathcal{D}}\left(f \nabla^{2} g-g \nabla^{2} f\right) d A=\int_{\partial \mathcal{D}}\left(f \frac{\partial g}{\partial n}-g \frac{\partial f}{\partial n}\right) d l$$

  where $\frac{\partial}{\partial n}$ denotes the outward normal derivative on $\partial \mathcal{D}$, and $f$ and $g$ are suitably regular functions that include the free space Green's function in two dimensions. You may also assume that the free space Green's function for the Laplace equation in two dimensions is given by

  $$G_{0}\left(\boldsymbol{r}, \boldsymbol{r}_{0}\right)=\frac{1}{2 \pi} \log \left|\boldsymbol{r}-\boldsymbol{r}_{0}\right|$$

  (a) State the conditions required on a function $G\left(\boldsymbol{r}, \boldsymbol{r}_{\mathbf{0}}\right)$ for it to be a Dirichlet Green's function for the Laplace operator on $\mathcal{D}$. Suppose that $\nabla^{2} \psi=0$ on $\mathcal{D}$. Show that if $G$ is a Dirichlet Green's function for $\mathcal{D}$ then

  $$\psi\left(\boldsymbol{r}_{\mathbf{0}}\right)=\int_{\partial \mathcal{D}} \psi(\boldsymbol{r}) \frac{\partial}{\partial n} G\left(\boldsymbol{r}, \boldsymbol{r}_{\mathbf{0}}\right) d l \quad \text { for } \boldsymbol{r}_{\mathbf{0}} \in \mathcal{D}$$

  (b) Consider the Laplace equation $\nabla^{2} \phi=0$ in the quarter space

  $$\mathcal{D}=\{(x, y): x \geqslant 0 \text { and } y \geqslant 0\}$$

  with boundary conditions

  $$\phi(x, 0)=e^{-x^{2}}, \phi(0, y)=e^{-y^{2}} \text { and } \phi(x, y) \rightarrow 0 \text { as } \sqrt{x^{2}+y^{2}} \rightarrow \infty$$

  Using the method of images, show that the solution is given by

  $$\phi\left(x_{0}, y_{0}\right)=F\left(x_{0}, y_{0}\right)+F\left(y_{0}, x_{0}\right),$$

  where

  $$F\left(x_{0}, y_{0}\right)=\frac{4 x_{0} y_{0}}{\pi} \int_{0}^{\infty} \frac{t e^{-t^{2}}}{\left[\left(t-x_{0}\right)^{2}+y_{0}^{2}\right]\left[\left(t+x_{0}\right)^{2}+y_{0}^{2}\right]} d t$$

  comment

• Paper 3, Section I, $3 E$

  Metric and Topological Spaces

  Part IB, 2016

  Let $X$ be a topological space and $A \subseteq X$ be a subset. A limit point of $A$ is a point $x \in X$ such that any open neighbourhood $U$ of $x$ intersects $A$. Show that $A$ is closed if and only if it contains all its limit points. Explain what is meant by the interior Int $(A)$ and the closure $\bar{A}$ of $A$. Show that if $A$ is connected, then $\bar{A}$ is connected.

  comment

• Paper 2, Section I, E

  Metric and Topological Spaces

  Part IB, 2016

  Consider $\mathbb{R}$ and $\mathbb{Q}$ with their usual topologies.

  (a) Show that compact subsets of a Hausdorff topological space are closed. Show that compact subsets of $\mathbb{R}$ are closed and bounded.

  (b) Show that there exists a complete metric space $(X, d)$ admitting a surjective continuous map $f: X \rightarrow \mathbb{Q}$.

  comment

• Paper 1, Section II, E

  Metric and Topological Spaces

  Part IB, 2016

  Let $p$ be a prime number. Define what is meant by the $p$-adic metric $d_{p}$ on $\mathbb{Q}$. Show that for $a, b, c \in \mathbb{Q}$ we have

  $$d_{p}(a, b) \leqslant \max \left\{d_{p}(a, c), d_{p}(c, b)\right\}$$

  Show that the sequence $\left(a_{n}\right)$, where $a_{n}=1+p+\cdots+p^{n-1}$, converges to some element in (D.

  For $a \in \mathbb{Q}$ define $|a|_{p}=d_{p}(a, 0)$. Show that if $a, b \in \mathbb{Q}$ and if $|a|_{p} \neq|b|_{p}$, then

  $$|a+b|_{p}=\max \left\{|a|_{p},|b|_{p}\right\} .$$

  Let $a \in \mathbb{Q}$ and let $B(a, \delta)$ be the open ball with centre $a$ and radius $\delta>0$, with respect to the metric $d_{p}$. Show that $B(a, \delta)$ is a closed subset of $\mathbb{Q}$ with respect to the topology induced by $d_{p}$.

  comment

• Paper 4, Section II, E

  Metric and Topological Spaces

  Part IB, 2016

  (a) Let $X$ be a topological space. Define what is meant by a quotient of $X$ and describe the quotient topology on the quotient space. Give an example in which $X$ is Hausdorff but the quotient space is not Hausdorff.

  (b) Let $T^{2}$ be the 2-dimensional torus considered as the quotient $\mathbb{R}^{2} / \mathbb{Z}^{2}$, and let $\pi: \mathbb{R}^{2} \rightarrow T^{2}$ be the quotient map.

  (i) Let $B(u, r)$ be the open ball in $\mathbb{R}^{2}$ with centre $u$ and radius $r<1 / 2$. Show that $U=\pi(B(u, r))$ is an open subset of $T^{2}$ and show that $\pi^{-1}(U)$ has infinitely many connected components. Show each connected component is homeomorphic to $B(u, r)$.

  (ii) Let $\alpha \in \mathbb{R}$ be an irrational number and let $L \subset \mathbb{R}^{2}$ be the line given by the equation $y=\alpha x$. Show that $\pi(L)$ is dense in $T^{2}$ but $\pi(L) \neq T^{2}$.

  comment

• Paper 1, Section I, D

  Numerical Analysis

  Part IB, 2016

  (a) What are real orthogonal polynomials defined with respect to an inner product $\langle\cdot, \cdot\rangle ?$ What does it mean for such polynomials to be monic?

  (b) Real monic orthogonal polynomials, $p_{n}(x)$, of degree $n=0,1,2, \ldots$, are defined with respect to the inner product,

  $$\langle p, q\rangle=\int_{-1}^{1} w(x) p(x) q(x) d x$$

  where $w(x)$ is a positive weight function. Show that such polynomials obey the three-term recurrence relation,

  $$p_{n+1}(x)=\left(x-\alpha_{n}\right) p_{n}(x)-\beta_{n} p_{n-1}(x),$$

  for appropriate $\alpha_{n}$ and $\beta_{n}$ which should be given in terms of inner products.

  comment

• Paper 4, Section I, D

  Numerical Analysis

  Part IB, 2016

  (a) Define the linear stability domain for a numerical method to solve $\mathbf{y}^{\prime}=\mathbf{f}(t, \mathbf{y})$. What is meant by an A-stable method?

  (b) A two-stage Runge-Kutta scheme is given by

  $$\mathbf{k}_{1}=\mathbf{f}\left(t_{n}, \mathbf{y}_{n}\right), \quad \mathbf{k}_{2}=\mathbf{f}\left(t_{n}+\frac{h}{2}, \mathbf{y}_{n}+\frac{h}{2} \mathbf{k}_{1}\right), \quad \mathbf{y}_{n+1}=\mathbf{y}_{n}+h \mathbf{k}_{2},$$

  where $h$ is the step size and $t_{n}=n h$. Show that the order of this scheme is at least two. For this scheme, find the intersection of the linear stability domain with the real axis. Hence show that this method is not A-stable.

  comment

• Paper 2, Section II, G

  Analysis II

  Part IB, 2016

  (a) What is a norm on a real vector space?

  (b) Let $L\left(\mathbb{R}^{m}, \mathbb{R}^{n}\right)$ be the space of linear maps from $\mathbb{R}^{m}$ to $\mathbb{R}^{n}$. Show that

  $$\|A\|=\sup _{0 \neq x \in \mathbb{R}^{m}} \frac{\|A x\|}{\|x\|}, \quad A \in L\left(\mathbb{R}^{m}, \mathbb{R}^{n}\right),$$

  defines a norm on $L\left(\mathbb{R}^{m}, \mathbb{R}^{n}\right)$, and that if $B \in L\left(\mathbb{R}^{\ell}, \mathbb{R}^{m}\right)$ then $\|A B\| \leqslant\|A\|\|B\|$.

  (c) Let $M_{n}$ be the space of $n \times n$ real matrices, identified with $L\left(\mathbb{R}^{n}, \mathbb{R}^{n}\right)$ in the usual way. Let $U \subset M_{n}$ be the subset

  $$U=\left\{X \in M_{n} \mid I-X \text { is invertible }\right\}$$

  Show that $U$ is an open subset of $M_{n}$ which contains the set $V=\left\{X \in M_{n} \mid\|X\|<1\right\}$.

  (d) Let $f: U \rightarrow M_{n}$ be the map $f(X)=(I-X)^{-1}$. Show carefully that the series $\sum_{k=0}^{\infty} X^{k}$ converges on $V$ to $f(X)$. Hence or otherwise, show that $f$ is twice differentiable at 0 , and compute its first and second derivatives there.

  comment

• Paper 1, Section II, D

  Numerical Analysis

  Part IB, 2016

  (a) Consider a method for numerically solving an ordinary differential equation (ODE) for an initial value problem, $\mathbf{y}^{\prime}=\mathbf{f}(t, \mathbf{y})$. What does it mean for a method to converge over $t \in[0, T]$ where $T \in \mathbb{R}$ ? What is the definition of the order of a method?

  (b) A general multistep method for the numerical solution of an ODE is

  $$\sum_{l=0}^{s} \rho_{l} \mathbf{y}_{n+l}=h \sum_{l=0}^{s} \sigma_{l} \mathbf{f}\left(t_{n+l}, \mathbf{y}_{n+l}\right), \quad n=0,1, \ldots$$

  where $s$ is a fixed positive integer. Show that this method is at least of order $p \geqslant 1$ if and only if

  $$\sum_{l=0}^{s} \rho_{l}=0 \quad \text { and } \quad \sum_{l=0}^{s} l^{k} \rho_{l}=k \sum_{l=0}^{s} l^{k-1} \sigma_{l}, \quad k=1, \ldots, p$$

  (c) State the Dahlquist equivalence theorem regarding the convergence of a multistep method.

  (d) Consider the multistep method,

  $$\mathbf{y}_{n+2}+\theta \mathbf{y}_{n+1}+a \mathbf{y}_{n}=h\left[\sigma_{0} \mathbf{f}\left(t_{n}, \mathbf{y}_{n}\right)+\sigma_{1} \mathbf{f}\left(t_{n+1}, \mathbf{y}_{n+1}\right)+\sigma_{2} \mathbf{f}\left(t_{n+2}, \mathbf{y}_{n+2}\right)\right]$$

  Determine the values of $\sigma_{i}$ and $a$ (in terms of the real parameter $\theta$ ) such that the method is at least third order. For what values of $\theta$ does the method converge?

  comment

• Paper 3, Section II, D

  Numerical Analysis

  Part IB, 2016

  (a) Determine real quadratic functions $a(x), b(x), c(x)$ such that the interpolation formula,

  $$f(x) \approx a(x) f(0)+b(x) f(2)+c(x) f(3),$$

  is exact when $f(x)$ is any real polynomial of degree 2 .

  (b) Use this formula to construct approximations for $f(5)$ and $f^{\prime}(1)$ which are exact when $f(x)$ is any real polynomial of degree 2 . Calculate these approximations for $f(x)=x^{3}$ and comment on your answers.

  (c) State the Peano kernel theorem and define the Peano kernel $K(\theta)$. Use this theorem to find the minimum values of the constants $\alpha$ and $\beta$ such that

  $$\left|f(1)-\frac{1}{3}[f(0)+3 f(2)-f(3)]\right| \leqslant \alpha \max _{\xi \in[0,3]}\left|f^{(2)}(\xi)\right|$$

  and

  $$\left|f(1)-\frac{1}{3}[f(0)+3 f(2)-f(3)]\right| \leqslant \beta\left\|f^{(2)}\right\|_{1}$$

  where $f \in C^{2}[0,3]$. Check that these inequalities hold for $f(x)=x^{3}$.

  comment

• Paper 2, Section II, D

  Numerical Analysis

  Part IB, 2016

  (a) Define a Givens rotation $\Omega^{[p, q]} \in \mathbb{R}^{m \times m}$ and show that it is an orthogonal matrix.

  (b) Define a QR factorization of a matrix $A \in \mathbb{R}^{m \times n}$ with $m \geqslant n$. Explain how Givens rotations can be used to find $Q \in \mathbb{R}^{m \times m}$ and $R \in \mathbb{R}^{m \times n}$.

  (c) Let

  $$\mathbf{A}=\left[\begin{array}{ccc} 3 & 1 & 1 \\ 0 & 4 & 1 \\ 0 & 3 & 2 \\ 0 & 0 & 3 / 4 \end{array}\right], \quad \mathbf{b}=\left[\begin{array}{c} 98 / 25 \\ 25 \\ 25 \\ 0 \end{array}\right]$$

  (i) Find a QR factorization of $A$ using Givens rotations.

  (ii) Hence find the vector $\mathbf{x}^{*} \in \mathbb{R}^{3}$ which minimises $\|A \mathbf{x}-\mathbf{b}\|$, where $\|\cdot\|$ is the Euclidean norm. What is $\left\|\mathrm{A} \mathbf{x}^{*}-\mathbf{b}\right\|$ ?

  comment

• Paper 1, Section I, H

  Optimization

  Part IB, 2016

  $$A=\left(\begin{array}{rrr} 5 & -2 & -5 \\ -2 & 3 & 2 \\ -3 & 6 & 2 \\ 4 & -8 & -6 \end{array}\right)$$

  be the payoff of a two-person zero-sum game, where player I (randomly) picks a row to maximise the expected payoff and player II picks a column to minimise the expected payoff. Find each player's optimal strategy and the value of the game.

  comment

• Paper 2, Section I, H

  Optimization

  Part IB, 2016

  Use the simplex algorithm to find the optimal solution to the linear program:

  $$\operatorname{maximise} 3 x+5 y \text { subject to } \begin{aligned} 8 x+3 y+10 z & \leqslant 9, \quad x, y, z \geqslant 0 \\ 5 x+2 y+4 z & \leqslant 8 \\ 2 x+y+3 z & \leqslant 2 \end{aligned}$$

  Write down the dual problem and find its solution.

  comment

• Paper 4, Section II, H

  Optimization

  Part IB, 2016

  (a) What is the maximal flow problem in a network? Explain the Ford-Fulkerson algorithm. Prove that this algorithm terminates if the initial flow is set to zero and all arc capacities are rational numbers.

  (b) Let $A=\left(a_{i, j}\right)_{i, j}$ be an $n \times n$ matrix. We say that $A$ is doubly stochastic if $0 \leqslant a_{i, j} \leqslant 1$ for $i, j$ and

  $$\begin{aligned} &\sum_{i=1}^{n} a_{i, j}=1 \text { for all } j \\ &\sum_{j=1}^{n} a_{i, j}=1 \text { for all } i \end{aligned}$$

  We say that $A$ is a permutation matrix if $a_{i, j} \in\{0,1\}$ for all $i, j$ and

  for all $j$ there exists a unique $i$ such that $a_{i, j}=1$,

  for all $i$ there exists a unique $j$ such that $a_{i, j}=1$.

  Let $\mathcal{C}$ be the set of all $n \times n$ doubly stochastic matrices. Show that a matrix $A$ is an extreme point of $\mathcal{C}$ if and only if $A$ is a permutation matrix.

  comment

• Paper 3, Section II, H

  Optimization

  Part IB, 2016

  (a) State and prove the Lagrangian sufficiency theorem.

  (b) Let $n \geqslant 1$ be a given constant, and consider the problem:

  $$\operatorname{minimise} \sum_{i=1}^{n}\left(2 y_{i}^{2}+x_{i}^{2}\right) \text { subject to } x_{i}=1+\sum_{k=1}^{i} y_{k} \text { for all } i=1, \ldots, n$$

  Find, with proof, constants $a, b, A, B$ such that the optimal solution is given by

  $$x_{i}=a 2^{i}+b 2^{-i} \text { and } y_{i}=A 2^{i}+B 2^{-i} \text {, for all } i=1, \ldots, n .$$

  comment

• Paper 4, Section I, B

  Quantum Mechanics

  Part IB, 2016

  (a) Define the quantum orbital angular momentum operator $\hat{\boldsymbol{L}}=\left(\hat{L}_{1}, \hat{L}_{2}, \hat{L}_{3}\right)$ in three dimensions, in terms of the position and momentum operators.

  (b) Show that $\left[\hat{L}_{1}, \hat{L}_{2}\right]=i \hbar \hat{L}_{3}$. [You may assume that the position and momentum operators satisfy the canonical commutation relations.]

  (c) Let $\hat{L}^{2}=\hat{L}_{1}^{2}+\hat{L}_{2}^{2}+\hat{L}_{3}^{2}$. Show that $\hat{L}_{1}$ commutes with $\hat{L}^{2}$.

  [In this part of the question you may additionally assume without proof the permuted relations $\left[\hat{L}_{2}, \hat{L}_{3}\right]=i \hbar \hat{L}_{1}$ and $\left.\left[\hat{L}_{3}, \hat{L}_{1}\right]=i \hbar \hat{L}_{2} .\right]$

  [Hint: It may be useful to consider the expression $[\hat{A}, \hat{B}] \hat{B}+\hat{B}[\hat{A}, \hat{B}]$ for suitable operators $\hat{A}$ and $\hat{B}$.]

  (d) Suppose that $\psi_{1}(x, y, z)$ and $\psi_{2}(x, y, z)$ are normalised eigenstates of $\hat{L}_{1}$ with eigenvalues $\hbar$ and $-\hbar$ respectively. Consider the wavefunction

  $$\psi=\frac{1}{2} \psi_{1} \cos \omega t+\frac{\sqrt{3}}{2} \psi_{2} \sin \omega t$$

  with $\omega$ being a positive constant. Find the earliest time $t_{0}>0$ such that the expectation value of $\hat{L}_{1}$ in $\psi$ is zero.

  comment

• Paper 3, Section I, B

  Quantum Mechanics

  Part IB, 2016

  (a) Consider a quantum particle moving in one space dimension, in a timeindependent real potential $V(x)$. For a wavefunction $\psi(x, t)$, define the probability density $\rho(x, t)$ and probability current $j(x, t)$ and show that

  $$\frac{\partial \rho}{\partial t}+\frac{\partial j}{\partial x}=0$$

  (b) Suppose now that $V(x)=0$ and $\psi(x, t)=\left(e^{i k x}+R e^{-i k x}\right) e^{-i E t / \hbar}$, where $E=\hbar^{2} k^{2} /(2 m), k$ and $m$ are real positive constants, and $R$ is a complex constant. Compute the probability current for this wavefunction. Interpret the terms in $\psi$ and comment on how this relates to the computed expression for the probability current.

  comment

• Paper 1, Section II, B

  Quantum Mechanics

  Part IB, 2016

  (a) A particle of mass $m$ in one space dimension is confined to move in a potential $V(x)$ given by

  $$V(x)= \begin{cases}0 & \text { for } 0<x<a \\ \infty & \text { for } x<0 \text { or } x>a\end{cases}$$

  The normalised initial wavefunction of the particle at time $t=0$ is

  $$\psi_{0}(x)=\frac{4}{\sqrt{5 a}} \sin ^{3}\left(\frac{\pi x}{a}\right)$$

  (i) Find the expectation value of the energy at time $t=0$.

  (ii) Find the wavefunction of the particle at time $t=1$.

  [Hint: It may be useful to recall the identity $\sin 3 \theta=3 \sin \theta-4 \sin ^{3} \theta$.]

  (b) The right hand wall of the potential is lowered to a finite constant value $U_{0}>0$ giving the new potential:

  $$U(x)= \begin{cases}0 & \text { for } 0<x<a \\ \infty & \text { for } x<0 \\ U_{0} & \text { for } x>a\end{cases}$$

  This potential is set up in the laboratory but the value of $U_{0}$ is unknown. The stationary states of the potential are investigated and it is found that there exists exactly one bound state. Show that the value of $U_{0}$ must satisfy

  $$\frac{\pi^{2} \hbar^{2}}{8 m a^{2}}<U_{0}<\frac{9 \pi^{2} \hbar^{2}}{8 m a^{2}}$$

  comment

• Paper 4, Section I, G

  Complex Analysis

  Part IB, 2016

  State carefully Rouché's theorem. Use it to show that the function $z^{4}+3+e^{i z}$ has exactly one zero $z=z_{0}$ in the quadrant

  $$\{z \in \mathbb{C} \mid 0<\arg (z)<\pi / 2\}$$

  and that $\left|z_{0}\right| \leqslant \sqrt{2}$.

  comment

• Paper 3, Section II, B

  Quantum Mechanics

  Part IB, 2016

  The spherically symmetric bound state wavefunctions $\psi(r)$ for the Coulomb potential $V=-e^{2} /\left(4 \pi \epsilon_{0} r\right)$ are normalisable solutions of the equation

  $$\frac{d^{2} \psi}{d r^{2}}+\frac{2}{r} \frac{d \psi}{d r}+\frac{2 \lambda}{r} \psi=-\frac{2 m E}{\hbar^{2}} \psi$$

  Here $\lambda=\left(m e^{2}\right) /\left(4 \pi \epsilon_{0} \hbar^{2}\right)$ and $E<0$ is the energy of the state.

  (a) By writing the wavefunction as $\psi(r)=f(r) \exp (-K r)$, for a suitable constant $K$ that you should determine, show that there are normalisable wavefunctions $\psi(r)$ only for energies of the form

  $$E=\frac{-m e^{4}}{32 \pi^{2} \epsilon_{0}^{2} \hbar^{2} N^{2}}$$

  with $N$ being a positive integer.

  (b) The energies in (a) reproduce the predictions of the Bohr model of the hydrogen atom. How do the wavefunctions above compare to the assumptions in the Bohr model?

  comment

• Paper 2, Section II, B

  Quantum Mechanics

  Part IB, 2016

  The one dimensional quantum harmonic oscillator has Hamiltonian

  $$\hat{H}=\frac{1}{2 m} \hat{p}^{2}+\frac{1}{2} m \omega^{2} \hat{x}^{2},$$

  where $m$ and $\omega$ are real positive constants and $\hat{x}$ and $\hat{p}$ are the standard position and momentum operators satisfying the commutation relation $[\hat{x}, \hat{p}]=i \hbar$. Consider the operators

  $$\hat{A}=\hat{p}-i m \omega \hat{x} \quad \text { and } \quad \hat{B}=\hat{p}+i m \omega \hat{x} .$$

  (a) Show that

  $$\hat{B} \hat{A}=2 m\left(\hat{H}-\frac{1}{2} \hbar \omega\right) \quad \text { and } \quad \hat{A} \hat{B}=2 m\left(\hat{H}+\frac{1}{2} \hbar \omega\right) .$$

  (b) Suppose that $\phi$ is an eigenfunction of $\hat{H}$ with eigenvalue $E$. Show that $\hat{A} \phi$ is then also an eigenfunction of $\hat{H}$ and that its corresponding eigenvalue is $E-\hbar \omega$.

  (c) Show that for any normalisable wavefunctions $\chi$ and $\psi$,

  $$\int_{-\infty}^{\infty} \chi^{*}(\hat{A} \psi) d x=\int_{-\infty}^{\infty}(\hat{B} \chi)^{*} \psi d x$$

  [You may assume that the operators $\hat{x}$ and $\hat{p}$ are Hermitian.]

  (d) With $\phi$ as in (b), obtain an expression for the norm of $\hat{A} \phi$ in terms of $E$ and the norm of $\phi$. [The squared norm of any wavefunction $\psi$ is $\int_{-\infty}^{\infty}|\psi|^{2} d x$.]

  (e) Show that all eigenvalues of $\hat{H}$ are non-negative.

  (f) Using the above results, deduce that each eigenvalue $E$ of $\hat{H}$ must be of the form $E=\left(n+\frac{1}{2}\right) \hbar \omega$ for some non-negative integer $n$.

  comment

• Paper 1, Section I, H

  Statistics

  Part IB, 2016

  Let $X_{1}, \ldots, X_{n}$ be independent samples from the exponential distribution with density $f(x ; \lambda)=\lambda e^{-\lambda x}$ for $x>0$, where $\lambda$ is an unknown parameter. Find the critical region of the most powerful test of size $\alpha$ for the hypotheses $H_{0}: \lambda=1$ versus $H_{1}: \lambda=2$. Determine whether or not this test is uniformly most powerful for testing $H_{0}^{\prime}: \lambda \leqslant 1$ versus $H_{1}^{\prime}: \lambda>1$.

  comment

• Paper 2, Section I, H

  Statistics

  Part IB, 2016

  The efficacy of a new medicine was tested as follows. Fifty patients were given the medicine, and another fifty patients were given a placebo. A week later, the number of patients who got better, stayed the same, or got worse was recorded, as summarised in this table:

  \begin{tabular}{|l|c|c|} \hline & medicine & placebo \ better & 28 & 22 \ same & 4 & 16 \ worse & 18 & 12 \ \hline \end{tabular}

  Conduct a Pearson chi-squared test of size $1 \%$ of the hypothesis that the medicine and the placebo have the same effect.

  [Hint: You may find the following values relevant:

  $\left.\begin{array}{lcccccc}\text { Distribution } & \chi_{1}^{2} & \chi_{2}^{2} & \chi_{3}^{2} & \chi_{4}^{2} & \chi_{5}^{2} & \chi_{6}^{2} \\ 99 \% \text { percentile } & 6.63 & 9.21 & 11.34 & 13.3 & 15.09 & 16.81 .\end{array}\right]$

  comment

• Paper 4, Section II, H

  Statistics

  Part IB, 2016

  Consider the linear regression model

  $$Y_{i}=\alpha+\beta x_{i}+\varepsilon_{i}$$

  for $i=1, \ldots, n$, where the non-zero numbers $x_{1}, \ldots, x_{n}$ are known and are such that $x_{1}+\ldots+x_{n}=0$, the independent random variables $\varepsilon_{1}, \ldots, \varepsilon_{n}$ have the $N\left(0, \sigma^{2}\right)$ distribution, and the parameters $\alpha, \beta$ and $\sigma^{2}$ are unknown.

  (a) Let $(\hat{\alpha}, \hat{\beta})$ be the maximum likelihood estimator of $(\alpha, \beta)$. Prove that for each $i$, the random variables $\hat{\alpha}, \hat{\beta}$ and $Y_{i}-\hat{\alpha}-\hat{\beta} x_{i}$ are uncorrelated. Using standard facts about the multivariate normal distribution, prove that $\hat{\alpha}, \hat{\beta}$ and $\sum_{i=1}^{n}\left(Y_{i}-\hat{\alpha}-\hat{\beta} x_{i}\right)^{2}$ are independent.

  (b) Find the critical region of the generalised likelihood ratio test of size $5 \%$ for testing $H_{0}: \alpha=0$ versus $H_{1}: \alpha \neq 0$. Prove that the power function of this test is of the form $w\left(\alpha, \beta, \sigma^{2}\right)=g(\alpha / \sigma)$ for some function $g$. [You are not required to find $g$ explicitly.]

  comment

• Paper 1, Section II, H

  Statistics

  Part IB, 2016

  (a) What does it mean to say a statistic $T$ is sufficient for an unknown parameter $\theta$ ? State the factorisation criterion for sufficiency and prove it in the discrete case.

  (b) State and prove the Rao-Blackwell theorem.

  (c) Let $X_{1}, \ldots, X_{n}$ be independent samples from the uniform distribution on $[-\theta, \theta]$ for an unknown positive parameter $\theta$. Consider the two-dimensional statistic

  $$T=\left(\min _{i} X_{i}, \max _{i} X_{i}\right) .$$

  Prove that $T$ is sufficient for $\theta$. Determine, with proof, whether or not $T$ is minimally sufficient.

  comment

• Paper 3, Section II, H

  Statistics

  Part IB, 2016

  Let $X_{1}, \ldots, X_{n}$ be independent samples from the Poisson distribution with mean $\theta$.

  (a) Compute the maximum likelihood estimator of $\theta$. Is this estimator biased?

  (b) Under the assumption that $n$ is very large, use the central limit theorem to find an approximate $95 \%$ confidence interval for $\theta$. [You may use the notation $z_{\alpha}$ for the number such that $\mathbb{P}\left(Z \geqslant z_{\alpha}\right)=\alpha$ for a standard normal $\left.Z \sim N(0,1) .\right]$

  (c) Now suppose the parameter $\theta$ has the $\Gamma(k, \lambda)$ prior distribution. What is the posterior distribution? What is the Bayes point estimator for $\theta$ for the quadratic loss function $L(\theta, a)=(\theta-a)^{2} ?$ Let $X_{n+1}$ be another independent sample from the same distribution. Given $X_{1}, \ldots, X_{n}$, what is the posterior probability that $X_{n+1}=0$ ?

  [Hint: The density of the $\Gamma(k, \lambda)$ distribution is $f(x ; k, \lambda)=\lambda^{k} x^{k-1} e^{-\lambda x} / \Gamma(k)$, for $x>0$.]

  comment

• Paper 1, Section I, C

  Variational Principles

  Part IB, 2016

  (a) Consider the function $f\left(x_{1}, x_{2}\right)=2 x_{1}^{2}+x_{2}^{2}+\alpha x_{1} x_{2}$, where $\alpha$ is a real constant. For what values of $\alpha$ is the function $f$ convex?

  (b) In the case $\alpha=-3$, calculate the extremum of $x_{1}^{2}$ on the set of points where $f\left(x_{1}, x_{2}\right)+1=0 .$

  comment

• Paper 3, Section I, C

  Variational Principles

  Part IB, 2016

  Two points $A$ and $B$ are located on the curved surface of the circular cylinder of radius $R$ with axis along the $z$-axis. We denote their locations by $\left(R, \phi_{A}, z_{A}\right)$ and $\left(R, \phi_{B}, z_{B}\right)$ using cylindrical polar coordinates and assume $\phi_{A} \neq \phi_{B}, z_{A} \neq z_{B}$. A path $\phi(z)$ is drawn on the cylinder to join $A$ and $B$. Show that the path of minimum distance between the points $A$ and $B$ is a helix, and determine its pitch. [For a helix with axis parallel to the $z$ axis, the pitch is the change in $z$ after one complete helical turn.]

  comment

• Paper 2, Section II, C

  Variational Principles

  Part IB, 2016

  A flexible wire filament is described by the curve $(x, y(x), z(x))$ in cartesian coordinates for $0 \leqslant x \leqslant L$. The filament is assumed to be almost straight and thus we assume $\left|y^{\prime}\right| \ll 1$ and $\left|z^{\prime}\right| \ll 1$ everywhere.

  (a) Show that the total length of the filament is approximately $L+\Delta$ where

  $$\Delta=\frac{1}{2} \int_{0}^{L}\left[\left(y^{\prime}\right)^{2}+\left(z^{\prime}\right)^{2}\right] d x$$

  (b) Under a uniform external axial force, $F>0$, the filament adopts the shape which minimises the total energy, $\mathcal{E}=E_{B}-F \Delta$, where $E_{B}$ is the bending energy given by

  $$E_{B}[y, z]=\frac{1}{2} \int_{0}^{L}\left[A(x)\left(y^{\prime \prime}\right)^{2}+B(x)\left(z^{\prime \prime}\right)^{2}\right] d x$$

  and where $A(x)$ and $B(x)$ are $x$-dependent bending rigidities (both known and strictly positive). The filament satisfies the boundary conditions

  $$y(0)=y^{\prime}(0)=z(0)=z^{\prime}(0)=0, \quad y(L)=y^{\prime}(L)=z(L)=z^{\prime}(L)=0$$

  Derive the Euler-Lagrange equations for $y(x)$ and $z(x)$.

  (c) In the case where $A=B=1$ and $L=1$, show that below a critical force, $F_{c}$, which should be determined, the only energy-minimising solution for the filament is straight $(y=z=0)$, but that a new nonzero solution is admissible at $F=F_{c}$.

  comment

• Paper 3, Section II, G

  Complex Analysis

  Part IB, 2016

  (a) Prove Cauchy's theorem for a triangle.

  (b) Write down an expression for the winding number $I(\gamma, a)$ of a closed, piecewise continuously differentiable curve $\gamma$ about a point $a \in \mathbb{C}$ which does not lie on $\gamma$.

  (c) Let $U \subset \mathbb{C}$ be a domain, and $f: U \rightarrow \mathbb{C}$ a holomorphic function with no zeroes in $U$. Suppose that for infinitely many positive integers $k$ the function $f$ has a holomorphic $k$-th root. Show that there exists a holomorphic function $F: U \rightarrow \mathbb{C}$ such that $f=\exp F$.

  comment

• Paper 4, Section II, C

  Variational Principles

  Part IB, 2016

  A fish swims in the ocean along a straight line with speed $V(t)$. The fish starts its journey from rest (zero velocity at $t=0$ ) and, during a given time $T$, swims subject to the constraint that the total distance travelled is $L$. The energy cost for swimming is $a V^{2}+b \dot{V}^{2}$ per unit time, where $a, b \geqslant 0$ are known and $a^{2}+b^{2} \neq 0$.

  (a) Derive the Euler-Lagrange condition on $V(t)$ for the journey to have minimum energetic cost.

  (b) In the case $a \neq 0, b \neq 0$ solve for $V(t)$ assuming that the fish starts at $t=0$ with zero acceleration (in addition to zero velocity).

  (c) In the case $a=0$, the fish can decide between three different boundary conditions for its journey. In addition to starting with zero velocity, it can:

  (1) start at $t=0$ with zero acceleration;

  (2) end at $t=T$ with zero velocity; or

  (3) end at $t=T$ with zero acceleration.

  Which of $(1),(2)$ or (3) is the best minimal-energy cost strategy?

  comment

• Paper 1, Section I, A

  Complex Analysis or Complex Methods

  Part IB, 2016

  Classify the singularities of the following functions at both $z=0$ and at the point at infinity on the extended complex plane:

  $$\begin{aligned} f_{1}(z) &=\frac{e^{z}}{z \sin ^{2} z}, \\ f_{2}(z) &=\frac{1}{z^{2}(1-\cos z)}, \\ f_{3}(z) &=z^{2} \sin (1 / z) \end{aligned}$$

  comment