(a) State Faraday's law of induction for a moving circuit in a time-dependent magnetic field and define all the terms that appear.

(b) Consider a rectangular circuit DEFG in the $z=0$ plane as shown in the diagram below. There are two rails parallel to the $x$-axis for $x>0$ starting at $\mathrm{D}$ at $(x, y)=(0,0)$ and $G$ at $(0, L)$. A battery provides an electromotive force $\mathcal{E}_{0}$ between $D$ and $G$ driving current in a positive sense around DEFG. The circuit is completed with a bar resistor of resistance $R$, length $L$ and mass $m$ that slides without friction on the rails; it connects $E$ at $(s(t), 0)$ and $F$ at $(s(t), L)$. The rest of the circuit has no resistance. The circuit is in a constant uniform magnetic field $B_{0}$ parallel to the $z$-axis.

[In parts (i)-(iv) you can neglect any magnetic field due to current flow.]

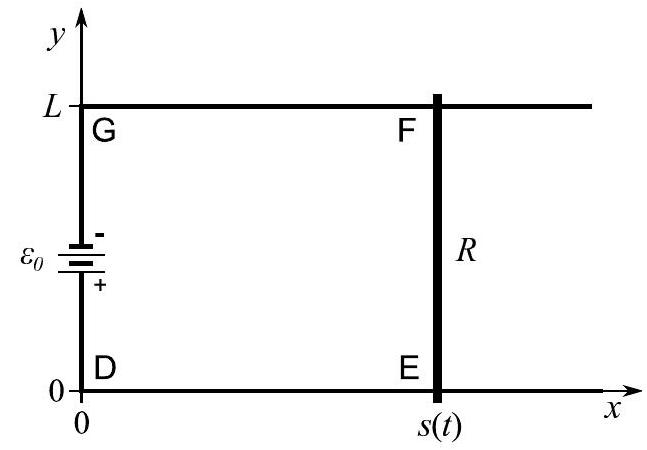
(i) Calculate the current in the bar and indicate its direction on a diagram of the circuit.

(ii) Find the force acting on the bar.

(iii) If the initial velocity and position of the bar are respectively $\dot{s}(0)=v_{0}>0$ and $s(0)=s_{0}>0$, calculate $\dot{s}(t)$ and $s(t)$ for $t>0$.

(iv) If $\mathcal{E}_{0}=0$, find the total energy dissipated in the circuit after $t=0$ and verify that total energy is conserved.

(v) Describe qualitatively the effect of the magnetic field caused by the induced current flowing in the circuit when $\mathcal{E}_{0}=0$.