Paper 2, Section II, H
Fix and let be the graph consisting of a copy of joining vertices and , a copy of joining vertices and , and a copy of joining vertices and . Let be the vertex adjacent to on the segment from to . Shown below is an illustration of in the case . The vertices are solid squares and edges are indicated by straight lines.
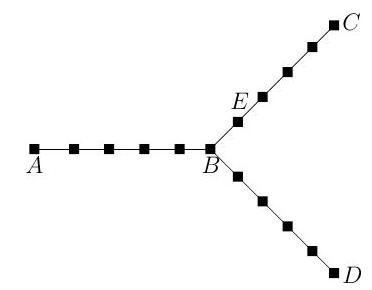
Let be a simple random walk on . In other words, in each time step, moves to one of its neighbours with equal probability. Assume that .
(a) Compute the expected amount of time for to hit .
(b) Compute the expected amount of time for to hit . [Hint: first show that the expected amount of time for to go from to satisfies where is the expected return time of to when starting from .]
(c) Compute the expected amount of time for to hit . [Hint: for each , let be the vertex which is places to the right of on the segment from to . Derive an equation for the expected amount of time for to go from to .]
Justify all of your answers.