Paper 4, Section II, H
Part IB, 2019
(a) State and prove the max-flow min-cut theorem.
(b) (i) Apply the Ford-Fulkerson algorithm to find the maximum flow of the network illustrated below, where is the source and is the sink.
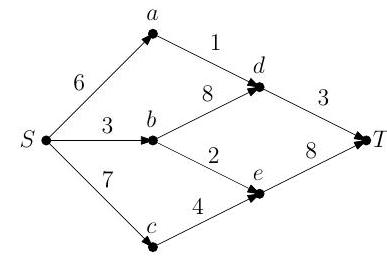
(ii) Verify the optimality of your solution using the max-flow min-cut theorem.
(iii) Is there a unique flow which attains the maximum? Explain your answer.
(c) Prove that the Ford-Fulkerson algorithm always terminates when the network is finite, the capacities are integers, and the algorithm is initialised where the initial flow is 0 across all edges. Prove also in this case that the flow across each edge is an integer.