A2.10
(i) Let be a directed network with nodes and . Let be a subset of the nodes, be a flow on , and be the divergence of . Describe carefully what is meant by a cut . Define the arc-cut incidence , and the flux of across . Define also the divergence of . Show that .
Now suppose that capacity constraints are specified on each of the arcs. Define the upper cut capacity of . State the feasible distribution problem for a specified divergence , and show that the problem only has a solution if and for all cuts .
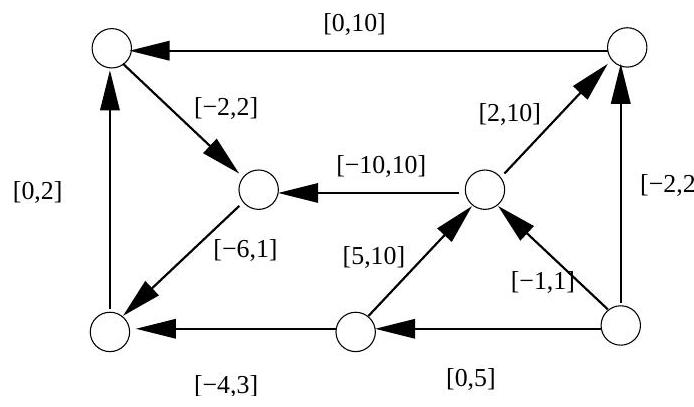
(ii) Describe an algorithm to find a feasible distribution given a specified divergence and capacity constraints on each arc. Explain what happens when no feasible distribution exists.
Illustrate the algorithm by either finding a feasible circulation, or demonstrating that one does not exist, in the network given below. Arcs are labelled with capacity constraint intervals.
Part II