A4.6
Define the terms homoclinic orbit, heteroclinic orbit and heteroclinic loop. In the case of a dynamical system that possesses a homoclinic orbit, explain, without detailed calculation, how to calculate its stability.
A second order dynamical system depends on two parameters and . When there is a heteroclinic loop between the points as in the diagram.
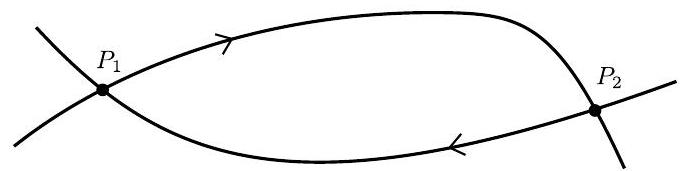
When are small there are trajectories that pass close to the fixed points : 
By adapting the method used above for trajectories near homoclinic orbits, show that the distances to the stable manifold at on successive returns are related to , , the corresponding distances near , by coupled equations of the form
where any arbitrary constants have been removed by rescaling, and depend on conditions near . Show from these equations that there is a stable heteroclinic orbit if . Show also that in the marginal situation there can be a stable fixed point for small positive if . Explain carefully the form of the orbit of the original dynamical system represented by the solution of the above map when .