A1.11 B1.16
(i) The prices, , of a stock in a binomial model at times are represented by the following binomial tree.
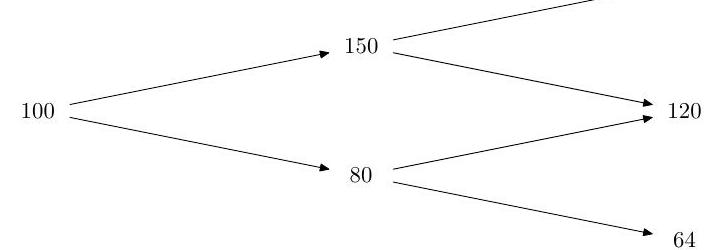
The fixed interest rate per period is and the probability that the stock price increases in a period is . Find the price at time 0 of a European call option with strike price 78 and expiry time
Explain briefly the ideas underlying your calculations.
(ii) Consider an investor in a one-period model who may invest in assets, all of which are risky, with a random return vector having mean and positivedefinite covariance matrix ; assume that not all the assets have the same expected return. Show that any minimum-variance portfolio is equivalent to the investor dividing his wealth between two portfolios, the global minimum-variance portfolio and the diversified portfolio, both of which should be specified clearly in terms of and .
Now suppose that where are independent random variables with having the exponential distribution with probability density function , where . Determine the global minimum-variance portfolio and the diversified portfolio explicitly.
Consider further the situation when the investor has the utility function , where denotes his wealth. Suppose that he acts to maximize the expected utility of his final wealth, and that his initial wealth is . Show that he now divides his wealth between the diversified portfolio and the uniform portfolio, in which wealth is apportioned equally between the assets, and determine the amounts that he invests in each.