A3.13 B3.21
Part II, 2002
(i) Two particles with angular momenta and basis states are combined to give total angular momentum and basis states . State the possible values of and show how a state with can be constructed. Briefly describe, for a general allowed value of , what the Clebsch-Gordan coefficients are.
(ii) If the angular momenta and are both 1 show that the combined state is
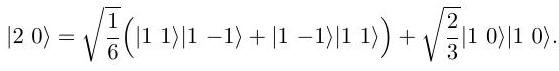
Determine the corresponding expressions for the combined states and , assuming that they are respectively antisymmetric and symmetric under interchange of the two particles.
If the combined system is in state what is the probability that measurements of the -component of angular momentum for either constituent particle will give the value of 1 ?
Hint: