A3.10
Part II, 2004
(i) Consider the problem
where and . State the Lagrange Sufficiency Theorem for problem . What is meant by saying that this problem is strong Lagrangian? How is this related to the Lagrange Sufficiency Theorem? Define a supporting hyperplane and state a condition guaranteeing that problem is strong Lagrangian.
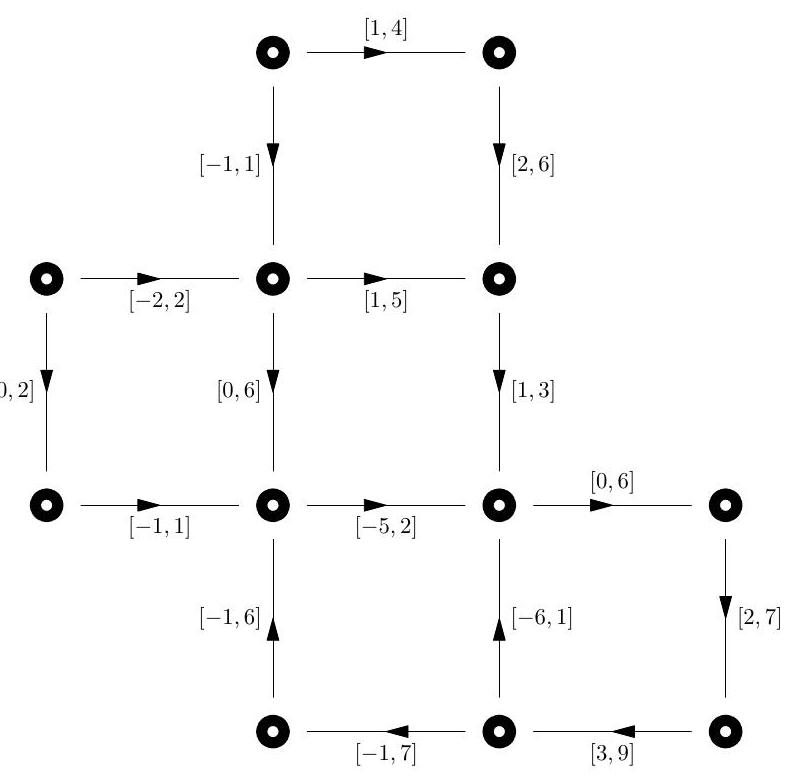
(ii) Define the terms flow, divergence, circulation, potential and differential for a network with nodes and .
State the feasible differential problem for a network with span intervals
State, without proof, the Feasible Differential Theorem.
[You must carefully define all quantities used in your statements.]
Show that the network below does not support a feasible differential.
Part II 2004