4.II.12G
Part II, 2005
For real and , give a careful definition of the -dimensional Hausdorff measure of and of the Hausdorff dimension of .
For , suppose is a similarity with contraction factor . Prove there is a unique non-empty compact invariant set for the . State a formula for the Hausdorff dimension of , under an assumption on the you should state.
Hence show the Hausdorff dimension of the fractal given by iterating the scheme below (at each stage replacing each edge by a new copy of the generating template) is .
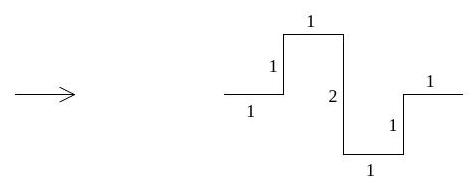
[Numbers denote lengths]