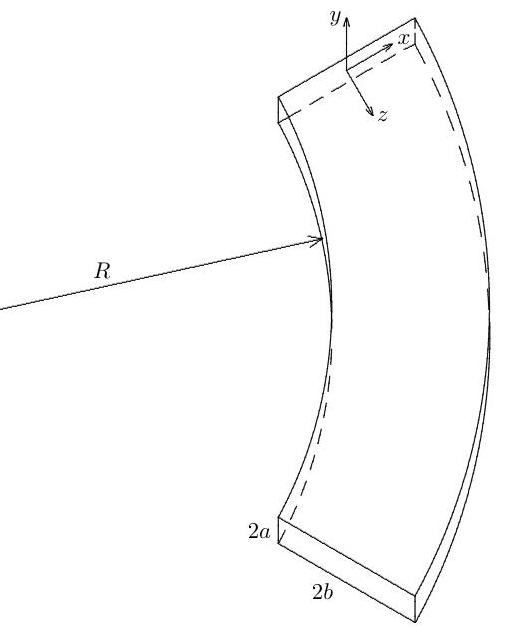
Viscous fluid of kinematic viscosity $\nu$ and density $\rho$ flows in a curved pipe of constant rectangular cross section and constant curvature. The cross-section has height $2 a$ and width $2 b$ (in the radial direction) with $b \gg a$, and the radius of curvature of the inner wall is $R$, with $R \gg b$. A uniform pressure gradient $-G$ is applied along the pipe.

(i) Assume to a first approximation that the pipe is straight, and ignore variation in the $x$-direction, where $(x, y, z)$ are Cartesian coordinates referred to an origin at the centre of the section, with $x$ increasing radially and $z$ measured along the pipe. Find the flow field along the pipe in the form $\mathbf{u}=(0,0, w(y))$.

(ii) It is given that the largest component of the inertial acceleration $\mathbf{u} \cdot \nabla \mathbf{u}$ due to the curvature of the pipe is $-w^{2} / R$ in the $x$ direction. Consider the secondary flow $\mathbf{u}_{s}$ induced in the $x, y$ plane, again ignoring variations in $x$ and any end effects (except for the requirement that there be zero total mass flux in the $x$ direction). Show that $\mathbf{u}_{s}$ takes the form $\mathbf{u}_{s}=(u(y), 0,0)$, where

$$u(y)=\frac{G^{2}}{120 \rho^{2} \nu^{3} R}\left(5 a^{2} y^{4}-y^{6}\right)+\frac{C}{2} y^{2}+D$$

and write down two equations determining the constants $C$ and $D$. [It is not necessary to solve these equations.]

Give conditions on the parameters that ensure that $|u| \ll|w|$.