1.II.13I
This problem deals with data collected as the number of each of two different strains of Ceriodaphnia organisms are counted in a controlled environment in which reproduction is occurring among the organisms. The experimenter places into the containers a varying concentration of a particular component of jet fuel that impairs reproduction. Hence it is anticipated that as the concentration of jet fuel grows, the mean number of organisms should decrease.
The table below gives a subset of the data. The full dataset has rows. The first column provides the number of organisms, the second the concentration of jet fuel (in grams per litre) and the third specifies the strain of the organism.
Explain and interpret the commands and (slightly abbreviated) output below. In particular, you should describe the model being fitted, explain how the standard errors are calculated, and comment on the hypothesis tests being described in the summary.
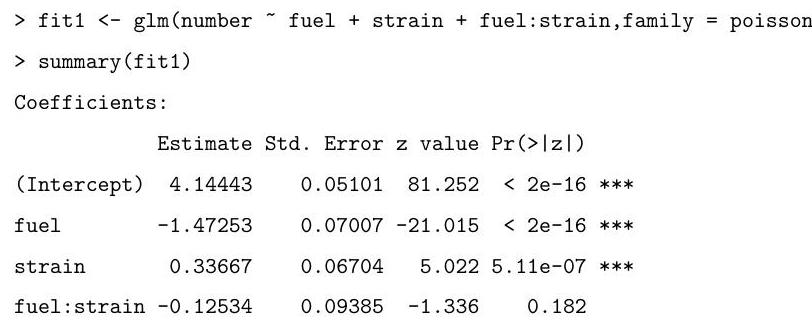
The following code fits two very similar models. Briefly explain the difference between these models and the one above. Motivate the fitting of these models in light of
Part II 2007 the summary from the fit of the one above.
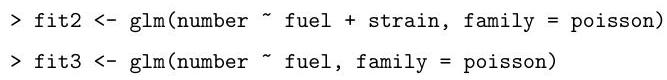
Denote by the three hypotheses being fitted in sequence above.
Explain the hypothesis tests, including an approximate test of the fit of , that can be performed using the output from the following code. Use these numbers to comment on the most appropriate model for the data.
, fit2$dev, fit3$dev)
[1]
[1]