Part II 2008

• 1.I.1H

  Number Theory

  Part II, 2008

  Define the continued fraction of a real number $\alpha$.

  Compute the continued fraction of $\sqrt{19}$.

  comment

• 2.I.1H

  Number Theory

  Part II, 2008

  What does it mean for a positive definite quadratic form with integer coefficients to be reduced?

  Show that there are precisely three reduced forms of this type with discriminant equal to $-23$.

  Which odd primes are properly represented by some positive definite binary quadratic form (with integer coefficients) of discriminant $-23$ ?

  comment

• $3 . \mathrm{I} . 2 \mathrm{~F} \quad$

  Topics in Analysis

  Part II, 2008

  (a) State the Baire category theorem in its closed sets version.

  (b) Let $f_{n}: \mathbf{R} \rightarrow \mathbf{R}$ be a continuous function for each $n=1,2,3, \ldots$ and suppose that there is a function $f: \mathbf{R} \rightarrow \mathbf{R}$ such that $f_{n}(x) \rightarrow f(x)$ for each $x \in \mathbf{R}$. Prove that for each $\epsilon>0$, there exists an integer $N_{0}$ and a non-empty open interval $I \subset \mathbf{R}$ such that $\left|f_{n}(x)-f(x)\right| \leqslant \epsilon$ for all $n \geqslant N_{0}$ and $x \in I$.

  [Hint: consider, for $N=1,2,3, \ldots$, the sets

  $$\left.Q_{N}=\left\{x \in \mathbf{R}:\left|f_{n}(x)-f_{m}(x)\right| \leqslant \epsilon: \forall n, m \geqslant N\right\} .\right]$$

  comment

• 2.II.26I

  Applied Probability

  Part II, 2008

  Consider a continuous-time Markov chain $\left(X_{t}\right)$ given by the diagram below.

  

  We will assume that the rates $\alpha, \beta, \lambda$ and $\mu$ are all positive.

  (a) Is the chain $\left(X_{t}\right)$ irreducible?

  (b) Write down the standard equations for the hitting probabilities

  $$h_{\mathrm{C} i}=\mathbb{P}_{\mathrm{C} i}(\text { hit W0) }, \quad i \geqslant 0,$$

  and

  $$h_{\mathrm{W} i}=\mathbb{P}_{\mathrm{W} i}(\text { hit W0) }, \quad i \geqslant 1 .$$

  Explain how to identify the probabilities $h_{\mathrm{C} i}$ and $h_{\mathrm{W} i}$ among the solutions to these equations.

  [You should state the theorem you use but its proof is not required.]

  (c) Set $h^{(i)}=\left(\begin{array}{c}h_{\mathrm{C} i} \\ h_{\mathrm{W} i}\end{array}\right)$ and find a matrix $A$ such that

  $$h^{(i)}=A h^{(i-1)}, \quad i=1,2, \ldots$$

  The recursion matrix $A$ has a 'standard' eigenvalue and a 'standard' eigenvector that do not depend on the transition rates: what are they and why are they always present?

  (d) Calculate the second eigenvalue $\vartheta$ of the matrix $A$, and the corresponding eigenvector, in the form $\left(\begin{array}{l}b \\ 1\end{array}\right)$, where $b>0$.

  (e) Suppose the second eigenvalue $\vartheta$ is $\geqslant 1$. What can you say about $h_{\mathrm{C} i}$ and $h_{\mathrm{W} i}$ ? Is the chain $\left(X_{t}\right)$ transient or recurrent? Justify your answer.

  (f) Now assume the opposite: the second eigenvalue $\vartheta$ is $<1$. Check that in this case $b<1$. Is the chain transient or recurrent under this condition?

  (g) Finally, specify, by means of inequalities between the parameters $\alpha, \beta, \lambda$ and $\mu$, when the chain $\left(X_{t}\right)$ is recurrent and when it is transient.

  comment

• 3.II.25I

  Applied Probability

  Part II, 2008

  Let $\left(X_{t}\right)$ be an irreducible continuous-time Markov chain with countably many states. What does it mean to say the chain is (i) positive recurrent, (ii) null recurrent? Consider the chain $\left(X_{t}\right)$ with the arrow diagram below.

  

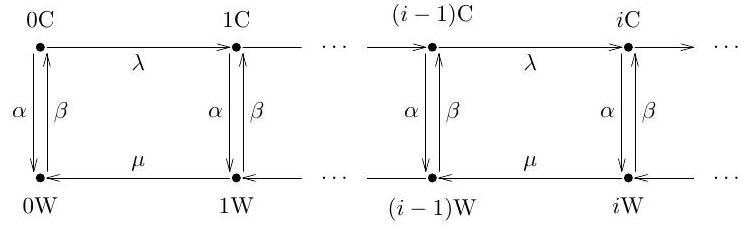
  In this question we analyse the existence of equilibrium probabilities $\pi_{i \mathrm{C}}$ and $\pi_{i \mathrm{~W}}$ of the chain $\left(X_{t}\right)$ being in state $i \mathrm{C}$ or $i \mathrm{~W}, i=0,1, \ldots$, and the impact of this fact on positive and null recurrence of the chain.

  (a) Write down the invariance equations $\pi Q=0$ and check that they have the form

  $$\begin{aligned} \pi_{0 C} &=\frac{\beta}{\lambda+\alpha} \pi_{0 \mathrm{~W}}, \\ \left(\pi_{1 \mathrm{C}}, \pi_{1 \mathrm{~W}}\right) &=\frac{\beta \pi_{0 \mathrm{~W}}}{\lambda+\alpha}\left(\frac{\lambda(\mu+\beta)}{\mu(\lambda+\alpha)}, \frac{\lambda}{\mu}\right) \\ \left(\pi_{(i+1) \mathrm{C}}, \pi_{(i+1) \mathrm{W}}\right) &=\left(\pi_{i \mathrm{C}}, \pi_{i \mathrm{~W}}\right) B, \quad i=1,2, \ldots, \end{aligned}$$

  where $B$ is a $2 \times 2$ recursion matrix:

  $$B=\left(\begin{array}{cc} \frac{\lambda \mu-\beta \alpha}{\mu(\lambda+\alpha)} & -\frac{\alpha}{\mu} \\ \frac{\beta(\beta+\mu)}{\mu(\lambda+\alpha)} & \frac{\beta+\mu}{\mu} \end{array}\right)$$

  (b) Verify that the row vector $\left(\pi_{1 \mathrm{C}}, \pi_{1 \mathrm{~W}}\right)$ is an eigenvector of $B$ with the eigenvalue $\theta$ where

  $$\theta=\frac{\lambda(\mu+\beta)}{\mu(\lambda+\alpha)}$$

  Hence, specify the form of equilibrium probabilities $\pi_{i \mathrm{C}}$ and $\pi_{i \mathrm{~W}}$ and conclude that the chain $\left(X_{t}\right)$ is positive recurrent if and only if $\mu \alpha>\lambda \beta$.

  comment

• 4.II.26I

  Applied Probability

  Part II, 2008

  On a hot summer night, opening my window brings some relief. This attracts hordes of mosquitoes who manage to negotiate a dense window net. But, luckily, I have a mosquito trapping device in my room.

  Assume the mosquitoes arrive in a Poisson process at rate $\lambda$; afterwards they wander around for independent and identically distributed random times with a finite mean $\mathbb{E} S$, where $S$ denotes the random wandering time of a mosquito, and finally are trapped by the device.

  (a) Identify a mathematical model, which was introduced in the course, for the number of mosquitoes present in the room at times $t \geqslant 0$.

  (b) Calculate the distribution of $Q(t)$ in terms of $\lambda$ and the tail probabilities $\mathbb{P}(S>x)$ of the wandering time $S$, where $Q(t)$ is the number of mosquitoes in the room at time $t>0$ (assuming that at the initial time, $Q(0)=0$ ).

  (c) Write down the distribution for $Q^{\mathrm{E}}$, the number of mosquitoes in the room in equilibrium, in terms of $\lambda$ and $\mathbb{E} S$.

  (d) Instead of waiting for the number of mosquitoes to reach equilibrium, I close the window at time $t>0$. For $v \geqslant 0$ let $X(t+v)$ be the number of mosquitoes left at time $t+v$, i.e. $v$ time units after closing the window. Calculate the distribution of $X(t+v)$.

  (e) Let $V(t)$ be the time needed to trap all mosquitoes in the room after closing the window at time $t>0$. By considering the event $\{X(t+v) \geqslant 1\}$, or otherwise, compute $\mathbb{P}[V(t)>v]$.

  (f) Now suppose that the time $t$ at which I shut the window is very large, so that I can assume that the number of mosquitoes in the room has the distribution of $Q^{E}$. Let $V^{E}$ be the further time needed to trap all mosquitoes in the room. Show that

  $$\mathbb{P}\left[V^{E}>v\right]=1-\exp \left(-\lambda \mathbb{E}\left[(S-v)_{+}\right]\right),$$

  where $x_{+} \equiv \max (x, 0)$.

  comment

• 1.II.27I

  Principles of Statistics

  Part II, 2008

  An angler starts fishing at time 0. Fish bite in a Poisson Process of rate $\Lambda$ per hour, so that, if $\Lambda=\lambda$, the number $N_{t}$ of fish he catches in the first $t$ hours has the Poisson distribution $\mathcal{P}(\lambda t)$, while $T_{n}$, the time in hours until his $n$th bite, has the Gamma distribution $\Gamma(n, \lambda)$, with density function

  $$p(t \mid \lambda)=\frac{\lambda^{n}}{(n-1) !} t^{n-1} e^{-\lambda t} \quad(t>0) .$$

  Bystander $B_{1}$ plans to watch for 3 hours, and to record the number $N_{3}$ of fish caught. Bystander $B_{2}$ plans to observe until the 10 th bite, and to record $T_{10}$, the number of hours until this occurs.

  For $B_{1}$, show that $\widetilde{\Lambda}_{1}:=N_{3} / 3$ is an unbiased estimator of $\Lambda$ whose variance function achieves the Cramér-Rao lower bound

  Find an unbiased estimator of $\Lambda$ for $B_{2}$, of the form $\widetilde{\Lambda}_{2}=k / T_{10}$. Does it achieve the Cramér-Rao lower bound? Is it minimum-variance-unbiased? Justify your answers.

  In fact, the 10 th fish bites after exactly 3 hours. For each of $B_{1}$ and $B_{2}$, write down the likelihood function for $\Lambda$ based their observations. What does the Likelihood Principle have to say about the inferences to be drawn by $B_{1}$ and $B_{2}$, and why? Compute the estimates $\tilde{\lambda}_{1}$ and $\widetilde{\lambda}_{2}$ produced by applying $\widetilde{\Lambda}_{1}$ and $\widetilde{\Lambda}_{2}$ to the observed data. Does the method of minimum-variance-unbiased estimation respect the Likelihood Principle?

  comment

• 2.II.27I

  Principles of Statistics

  Part II, 2008

  Under hypothesis $H_{i}(i=0,1)$, a real-valued observable $X$, taking values in $\mathcal{X}$, has density function $p_{i}(\cdot)$. Define the Type I error $\alpha$ and the Type II error $\beta$ of a test $\phi: \mathcal{X} \rightarrow[0,1]$ of the null hypothesis $H_{0}$ against the alternative hypothesis $H_{1}$. What are the size and power of the test in terms of $\alpha$ and $\beta$ ?

  Show that, for $0<c<\infty, \phi$ minimises $c \alpha+\beta$ among all possible tests if and only if it satisfies

  $$\begin{aligned} &p_{1}(x)>c p_{0}(x) \Rightarrow \phi(x)=1 \\ &p_{1}(x)<c p_{0}(x) \Rightarrow \phi(x)=0 \end{aligned}$$

  What does this imply about the admissibility of such a test?

  Given the value $\theta$ of a parameter variable $\Theta \in[0,1)$, the observable $X$ has density function

  $$p(x \mid \theta)=\frac{2(x-\theta)}{(1-\theta)^{2}} \quad(\theta \leqslant x \leqslant 1)$$

  For fixed $\theta \in(0,1)$, describe all the likelihood ratio tests of $H_{0}: \Theta=0$ against $H_{\theta}: \Theta=\theta$.

  For fixed $k \in(0,1)$, let $\phi_{k}$ be the test that rejects $H_{0}$ if and only if $X \geqslant k$. Is $\phi_{k}$ admissible as a test of $H_{0}$ against $H_{\theta}$ for every $\theta \in(0,1)$ ? Is it uniformly most powerful for its size for testing $H_{0}$ against the composite hypothesis $H_{1}: \Theta \in(0,1)$ ? Is it admissible as a test of $H_{0}$ against $H_{1}$ ?

  comment

• 3.II.26I

  Principles of Statistics

  Part II, 2008

  Define the notion of exponential family $(E F)$, and show that, for data arising as a random sample of size $n$ from an exponential family, there exists a sufficient statistic whose dimension stays bounded as $n \rightarrow \infty$.

  The log-density of a normal distribution $\mathcal{N}(\mu, v)$ can be expressed in the form

  $$\log p(x \mid \boldsymbol{\phi})=\phi_{1} x+\phi_{2} x^{2}-k(\boldsymbol{\phi})$$

  where $\phi=\left(\phi_{1}, \phi_{2}\right)$ is the value of an unknown parameter $\Phi=\left(\Phi_{1}, \Phi_{2}\right)$. Determine the function $k$, and the natural parameter-space $\mathbb{F}$. What is the mean-value parameter $\mathrm{H}=\left(\mathrm{H}_{1}, \mathrm{H}_{2}\right)$ in terms of $\Phi ?$

  Determine the maximum likelihood estimator $\widehat{\Phi}_{1}$ of $\Phi_{1}$ based on a random sample $\left(X_{1}, \ldots, X_{n}\right)$, and give its asymptotic distribution for $n \rightarrow \infty$.

  How would these answers be affected if the variance of $X$ were known to have value $v_{0}$ ?

  comment

• 4.II.27I

  Principles of Statistics

  Part II, 2008

  Define sufficient statistic, and state the factorisation criterion for determining whether a statistic is sufficient. Show that a Bayesian posterior distribution depends on the data only through the value of a sufficient statistic.

  Given the value $\mu$ of an unknown parameter $M$, observables $X_{1}, \ldots, X_{n}$ are independent and identically distributed with distribution $\mathcal{N}(\mu, 1)$. Show that the statistic $\bar{X}:=n^{-1} \sum_{i=1}^{n} X_{i}$ is sufficient for $\mathrm{M}$.

  If the prior distribution is $\mathrm{M} \sim \mathcal{N}\left(0, \tau^{2}\right)$, determine the posterior distribution of $\mathrm{M}$ and the predictive distribution of $\bar{X}$.

  In fact, there are two hypotheses as to the value of M. Under hypothesis $H_{0}$, $\mathrm{M}$ takes the known value 0 ; under $H_{1}, \mathrm{M}$ is unknown, with prior distribution $\mathcal{N}\left(0, \tau^{2}\right)$. Explain why the Bayes factor for choosing between $H_{0}$ and $H_{1}$ depends only on $\bar{X}$, and determine its value for data $X_{1}=x_{1}, \ldots, X_{n}=x_{n}$.

  The frequentist $5 \%$-level test of $H_{0}$ against $H_{1}$ rejects $H_{0}$ when $|\bar{X}| \geqslant 1.96 / \sqrt{n}$. What is the Bayes factor for the critical case $|\bar{x}|=1.96 / \sqrt{n}$ ? How does this behave as $n \rightarrow \infty$ ? Comment on the similarities or differences in behaviour between the frequentist and Bayesian tests.

  comment

• 1.II.28J

  Stochastic Financial Models

  Part II, 2008

  (a) In the context of the Black-Scholes formula, let $S_{0}$ be the time- 0 spot price, $K$ be the strike price, $T$ be the time to maturity, and let $\sigma$ be the volatility. Assume that the interest rate $r$ is constant and assume absence of dividends. Write $\mathrm{EC}\left(S_{0}, K, \sigma, r, T\right)$ for the time- 0 price of a standard European call. The Black-Scholes formula can be written in the following form

  $$\operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)=S_{0} \Phi\left(d_{1}\right)-e^{-r T} K \Phi\left(d_{2}\right)$$

  State how the quantities $d_{1}$ and $d_{2}$ depend on $S_{0}, K, \sigma, r$ and $T$.

  Assume that you sell this option at time 0 . What is your replicating portfolio at time 0 ?

  [No proofs are required.]

  (b) Compute the limit of $\operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)$ as $\sigma \rightarrow \infty$. Construct an explicit arbitrage under the assumption that European calls are traded above this limiting price.

  (c) Compute the limit of $\operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)$ as $\sigma \rightarrow 0$. Construct an explicit arbitrage under the assumption that European calls are traded below this limiting price.

  (d) Express in terms of $S_{0}, d_{1}$ and $T$ the derivative

  $$\frac{\partial}{\partial \sigma} \operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)$$

  [Hint: you may find it useful to express $\frac{\partial}{\partial \sigma} d_{1}$ in terms of $\frac{\partial}{\partial \sigma} d_{2}$.]

  [You may use without proof the formula $S_{0} \Phi^{\prime}\left(d_{1}\right)-e^{-r T} K \Phi^{\prime}\left(d_{2}\right)=0$.]

  (e) Say what is meant by implied volatility and explain why the previous results make it well-defined.

  comment

• 2.II.28J

  Stochastic Financial Models

  Part II, 2008

  (a) Let $\left(B_{t}: t \geqslant 0\right)$ be a Brownian motion and consider the process

  $$Y_{t}=Y_{0} e^{\sigma B_{t}+\left(\mu-\frac{1}{2} \sigma^{2}\right) t}$$

  for $Y_{0}>0$ deterministic. For which values of $\mu$ is $\left(Y_{t}: t \geqslant 0\right)$ a supermartingale? For which values of $\mu$ is $\left(Y_{t}: t \geqslant 0\right)$ a martingale? For which values of $\mu$ is $\left(1 / Y_{t}: t \geqslant 0\right)$ a martingale? Justify your answers.

  (b) Assume that the riskless rates of return for Dollar investors and Euro investors are $r_{D}$ and $r_{E}$ respectively. Thus, 1 Dollar at time 0 in the bank account of a Dollar investor will grow to $e^{r_{D} t}$ Dollars at time $t$. For a Euro investor, the Dollar is a risky, tradable asset. Let $\mathbb{Q}_{E}$ be his equivalent martingale measure and assume that the EUR/USD exchange rate at time $t$, that is, the number of Euros that one Dollar will buy at time $t$, is given by

  $$Y_{t}=Y_{0} e^{\sigma B_{t}+\left(\mu-\frac{1}{2} \sigma^{2}\right) t},$$

  where $\left(B_{t}\right)$ is a Brownian motion under $\mathbb{Q}_{E}$. Determine $\mu$ as function of $r_{D}$ and $r_{E}$. Verify that $Y$ is a martingale if $r_{D}=r_{E}$.

  (c) Let $r_{D}, r_{E}$ be as in part (b). Let now $\mathbb{Q}_{D}$ be an equivalent martingale measure for a Dollar investor and assume that the EUR/USD exchange rate at time $t$ is given by

  $$Y_{t}=Y_{0} e^{\sigma B_{t}+\left(\mu-\frac{1}{2} \sigma^{2}\right) t}$$

  where now $\left(B_{t}\right)$ is a Brownian motion under $\mathbb{Q}_{D}$. Determine $\mu$ as function of $r_{D}$ and $r_{E}$. Given $r_{D}=r_{E}$, check, under $\mathbb{Q}_{D}$, that is $Y$ is not a martingale but that $1 / Y$ is a martingale.

  (d) Assuming still that $r_{D}=r_{E}$, rederive the final conclusion of part (c), namely the martingale property of $1 / Y$, directly from part (b).

  comment

• 3.II.27J

  Stochastic Financial Models

  Part II, 2008

  Consider a vector of asset prices evolving over time $\bar{S}=\left(S_{t}^{0}, S_{t}^{1}, \ldots, S_{t}^{d}\right)_{t \in\{0,1, \ldots, T\}}$. The asset price $S^{0}$ is assumed constant over time. In this context, explain what is an arbitrage and prove that the existence of an equivalent martingale measure implies noarbitrage.

  Suppose that over two periods a stock price moves on a binomial tree

  

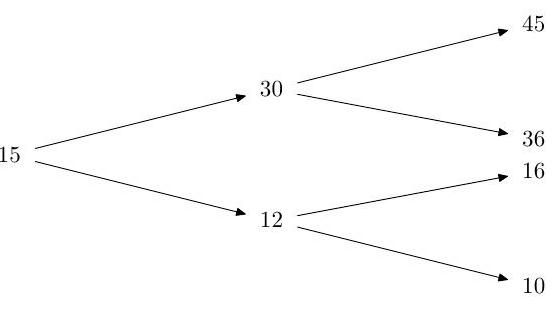
  Assume riskless rate $r=1 / 4$. Determine the equivalent martingale measure. [No proof is required.]

  Sell an American put with strike 15 and expiry 2 at its no-arbitrage price, which you should determine.

  Verify that the buyer of the option should use his early exercise right if the first period is bad.

  Assume that the first period is bad, and that the buyer forgets to exercise. How much risk-free profit can you lock in?

  comment

• 4.I.2F

  Topics in Analysis

  Part II, 2008

  (a) State Runge's theorem on uniform approximation of analytic functions by polynomials.

  (b) Suppose $f$ is analytic on

  $$\Omega=\{z \in \mathbf{C}:|z|<1\} \backslash\{z \in \mathbf{C}: \operatorname{Im}(z)=0, \operatorname{Re}(z) \leqslant 0\} .$$

  Prove that there exists a sequence of polynomials which converges to $f$ uniformly on compact subsets of $\Omega$.

  comment

• 4.II.28J

  Stochastic Financial Models

  Part II, 2008

  (a) Consider a family $\left(X_{n}: n \geqslant 0\right)$ of independent, identically distributed, positive random variables and fix $z_{0}>0$. Define inductively

  $$z_{n+1}=z_{n} X_{n}, \quad n \geqslant 0$$

  Compute, for $n \in\{1, \ldots, N\}$, the conditional expectation $\mathbb{E}\left(z_{N} \mid z_{n}\right)$.

  (b) Fix $R \in[0,1)$. In the setting of part (a), compute also $\mathbb{E}\left(U\left(z_{N}\right) \mid z_{n}\right)$, where

  $$U(x)=x^{1-R} /(1-R), \quad x \geqslant 0 .$$

  (c) Let $U$ be as in part (b). An investor with wealth $w_{0}>0$ at time 0 wishes to invest it in such a way as to maximise $\mathbb{E}\left(U\left(w_{N}\right)\right)$ where $w_{N}$ is the wealth at the start of day $N$. Let $\alpha \in[0,1]$ be fixed. On day $n$, he chooses the proportion $\theta \in[\alpha, 1]$ of his wealth to invest in a single risky asset, so that his wealth at the start of day $n+1$ will be

  $$w_{n+1}=w_{n}\left\{\theta X_{n}+(1-\theta)(1+r)\right\}$$

  Here, $\left(X_{n}: n \geqslant 0\right)$ is as in part (a) and $r$ is the per-period riskless rate of interest. If $V_{n}(w)=\sup \mathbb{E}\left(U\left(w_{N}\right) \mid w_{n}=w\right)$ denotes the value function of this optimization problem, show that $V_{n}\left(w_{n}\right)=a_{n} U\left(w_{n}\right)$ and give a formula for $a_{n}$. Verify that, in the case $\alpha=1$, your answer is in agreement with part (b).

  comment

• 2.II.29I

  Optimization and Control

  Part II, 2008

  Consider a stochastic controllable dynamical system $P$ with action-space $A$ and countable state-space $S$. Thus $P=\left(p_{x y}(a): x, y \in S, a \in A\right)$ and $p_{x y}(a)$ denotes the transition probability from $x$ to $y$ when taking action $a$. Suppose that a cost $c(x, a)$ is incurred each time that action $a$ is taken in state $x$, and that this cost is uniformly bounded. Write down the dynamic optimality equation for the problem of minimizing the expected long-run average cost.

  State in terms of this equation a general result, which can be used to identify an optimal control and the minimal long-run average cost.

  A particle moves randomly on the integers, taking steps of size 1 . Suppose we can choose at each step a control parameter $u \in[\alpha, 1-\alpha]$, where $\alpha \in(0,1 / 2)$ is fixed, which has the effect that the particle moves in the positive direction with probability $u$ and in the negative direction with probability $1-u$. It is desired to maximize the long-run proportion of time $\pi$ spent by the particle at 0 . Show that there is a solution to the optimality equation for this example in which the relative cost function takes the form $\theta(x)=\mu|x|$, for some constant $\mu$.

  Determine an optimal control and show that the maximal long-run proportion of time spent at 0 is given by

  $$\pi=\frac{1-2 \alpha}{2(1-\alpha)} .$$

  You may assume that it is valid to use an unbounded function $\theta$ in the optimality equation in this example.

  comment

• 3.II.28I

  Optimization and Control

  Part II, 2008

  Let $Q$ be a positive-definite symmetric $m \times m$ matrix. Show that a non-negative quadratic form on $\mathbb{R}^{d} \times \mathbb{R}^{m}$ of the form

  $$c(x, a)=x^{T} R x+x^{T} S^{T} a+a^{T} S x+a^{T} Q a, \quad x \in \mathbb{R}^{d}, \quad a \in \mathbb{R}^{m}$$

  is minimized over $a$, for each $x$, with value $x^{T}\left(R-S^{T} Q^{-1} S\right) x$, by taking $a=K x$, where $K=-Q^{-1} S$.

  Consider for $k \leqslant n$ the controllable stochastic linear system in $\mathbb{R}^{d}$

  $$X_{j+1}=A X_{j}+B U_{j}+\varepsilon_{j+1}, \quad j=k, k+1, \ldots, n-1,$$

  starting from $X_{k}=x$ at time $k$, where the control variables $U_{j}$ take values in $\mathbb{R}^{m}$, and where $\varepsilon_{k+1}, \ldots, \varepsilon_{n}$ are independent, zero-mean random variables, with $\operatorname{var}\left(\varepsilon_{j}\right)=N_{j}$. Here, $A, B$ and $N_{j}$ are, respectively, $d \times d, d \times m$ and $d \times d$ matrices. Assume that a cost $c\left(X_{j}, U_{j}\right)$ is incurred at each time $j=k, \ldots, n-1$ and that a final cost $C\left(X_{n}\right)=X_{n}^{T} \Pi_{0} X_{n}$ is incurred at time $n$. Here, $\Pi_{0}$ is a given non-negative-definite symmetric matrix. It is desired to minimize, over the set of all controls $u$, the total expected cost $V^{u}(k, x)$. Write down the optimality equation for the infimal cost function $V(k, x)$.

  Hence, show that $V(k, x)$ has the form

  $$V(k, x)=x^{T} \Pi_{n-k} x+\gamma_{k}$$

  for some non-negative-definite symmetric matrix $\Pi_{n-k}$ and some real constant $\gamma_{k}$. Show how to compute the matrix $\Pi_{n-k}$ and constant $\gamma_{k}$ and how to determine an optimal control.

  comment

• 4.II.29I

  Optimization and Control

  Part II, 2008

  State Pontryagin's maximum principle for the controllable dynamical system with state-space $\mathbb{R}^{+}$, given by

  $$\dot{x}_{t}=b\left(t, x_{t}, u_{t}\right), \quad t \geqslant 0,$$

  where the running costs are given by $c\left(t, x_{t}, u_{t}\right)$, up to an unconstrained terminal time $\tau$ when the state first reaches 0 , and there is a terminal cost $C(\tau)$.

  A company pays a variable price $p(t)$ per unit time for electrical power, agreed in advance, which depends on the time of day. The company takes on a job at time $t=0$, which requires a total amount $E$ of electrical energy, but can be processed at a variable level of power consumption $u(t) \in[0,1]$. If the job is completed by time $\tau$, then the company will receive a reward $R(\tau)$. Thus, it is desired to minimize

  $$\int_{0}^{\tau} u(t) p(t) d t-R(\tau)$$

  subject to

  $$\int_{0}^{\tau} u(t) d t=E, \quad u(t) \in[0,1],$$

  with $\tau>0$ unconstrained. Take as state variable the energy $x_{t}$ still needed at time $t$ to complete the job. Use Pontryagin's maximum principle to show that the optimal control is to process the job on full power or not at all, according as the price $p(t)$ lies below or above a certain threshold value $p^{*}$.

  Show further that, if $\tau^{*}$ is the completion time for the optimal control, then

  $$p^{*}+\dot{R}\left(\tau^{*}\right)=p\left(\tau^{*}\right)$$

  Consider a case in which $p$ is periodic, with period one day, where day 1 corresponds to the time interval $[0,2]$, and $p(t)=(t-1)^{2}$ during day 1 . Suppose also that $R(\tau)=1 /(1+\tau)$ and $E=1 / 2$. Determine the total energy cost and the reward associated with the threshold $p^{*}=1 / 4$.

  Hence, show that any threshold low enough to carry processing over into day 2 is suboptimal.

  Show carefully that the optimal price threshold is given by $p^{*}=1 / 4$.

  comment

• 1.II.29C

  Partial Differential Equations

  Part II, 2008

  (i) State the local existence theorem for the first order quasi-linear partial differential equation

  $$\sum_{j=1}^{n} a_{j}(x, u) \frac{\partial u}{\partial x_{j}}=b(x, u)$$

  which is to be solved for a real-valued function with data specified on a hypersurface $S$. Include a definition of "non-characteristic" in your answer.

  (ii) Consider the linear constant-coefficient case (that is, when all the functions $a_{1}, \ldots, a_{n}$ are real constants and $b(x, u)=c x+d$ for some $c=\left(c_{1}, \ldots, c_{n}\right)$ with $c_{1}, \ldots, c_{n}$ real and $d$ real) and with the hypersurface $S$ taken to be the hyperplane $\mathbf{x} \cdot \mathbf{n}=0$. Explain carefully the relevance of the non-characteristic condition in obtaining a solution via the method of characteristics.

  (iii) Solve the equation

  $$\frac{\partial u}{\partial y}+u \frac{\partial u}{\partial x}=0$$

  with initial data $u(0, y)=-y$ prescribed on $x=0$, for a real-valued function $u(x, y)$. Describe the domain on which your solution is $C^{1}$ and comment on this in relation to the theorem stated in (i).

  comment

• 2.II.30C

  Partial Differential Equations

  Part II, 2008

  (i) Define the concept of "fundamental solution" of a linear constant-coefficient partial differential operator and write down the fundamental solution for the operator $-\Delta$ on $\mathbb{R}^{3}$.

  (ii) State and prove the mean value property for harmonic functions on $\mathbb{R}^{3}$.

  (iii) Let $u \in C^{2}\left(\mathbb{R}^{3}\right)$ be a harmonic function which satisfies $u(p) \geqslant 0$ at every point $p$ in an open set $\Omega \subset \mathbb{R}^{3}$. Show that if $B(z, r) \subset B(w, R) \subset \Omega$, then

  $$u(w) \geqslant\left(\frac{r}{R}\right)^{3} u(z) .$$

  Assume that $B(x, 4 r) \subset \Omega$. Deduce, by choosing $R=3 r$ and $w, z$ appropriately, that

  $$\inf _{B(x, r)} u \geqslant 3^{-3} \sup _{B(x, r)} u .$$

  [In (iii), $B(z, \rho)=\left\{x \in \mathbb{R}^{3}:\|x-z\|<\rho\right\}$ is the ball of radius $\rho>0$ centred at $\left.z \in \mathbb{R}^{3} \cdot\right]$

  comment

• 3.II.29C

  Partial Differential Equations

  Part II, 2008

  Let $C_{p e r}^{\infty}=\left\{u \in C^{\infty}(\mathbb{R}): u(x+2 \pi)=u(x)\right\}$ be the space of smooth $2 \pi$-periodic functions of one variable.

  (i) For $f \in C_{p e r}^{\infty}$ show that there exists a unique $u_{f} \in C_{p e r}^{\infty}$ such that

  $$-\frac{d^{2} u_{f}}{d x^{2}}+u_{f}=f$$

  (ii) Show that $I_{f}\left[u_{f}+\phi\right]>I_{f}\left[u_{f}\right]$ for every $\phi \in C_{p e r}^{\infty}$ which is not identically zero, where $I_{f}: C_{p e r}^{\infty} \rightarrow \mathbb{R}$ is defined by

  $$I_{f}[u]=\frac{1}{2} \int_{-\pi}^{+\pi}\left[\left(\frac{\partial u}{\partial x}\right)^{2}+u^{2}-2 f(x) u\right] d x$$

  (iii) Show that the equation

  $$\frac{\partial u}{\partial t}-\frac{\partial^{2} u}{\partial x^{2}}+u=f(x)$$

  with initial data $u(0, x)=u_{0}(x) \in C_{\text {per }}^{\infty}$ has, for $t>0$, a smooth solution $u(t, x)$ such that $u(t, \cdot) \in C_{p e r}^{\infty}$ for each fixed $t>0$. Give a representation of this solution as a Fourier series in $x$. Calculate $\lim _{t \rightarrow+\infty} u(t, x)$ and comment on your answer in relation to (i).

  (iv) Show that $I_{f}[u(t, \cdot)] \leqslant I_{f}[u(s, \cdot)]$ for $t>s>0$, and that $I_{f}[u(t, \cdot)] \rightarrow I_{f}\left[u_{f}\right]$ as $t \rightarrow+\infty$.

  comment

• 4.II.30C

  Partial Differential Equations

  Part II, 2008

  (i) Define the Fourier transform $\hat{f}=\mathcal{F}(f)$ of a Schwartz function $f \in \mathcal{S}\left(\mathbb{R}^{n}\right)$, and also of a tempered distribution $u \in \mathcal{S}^{\prime}\left(\mathbb{R}^{n}\right)$.

  (ii) From your definition, compute the Fourier transform of the distribution $W_{t} \in \mathcal{S}^{\prime}\left(\mathbb{R}^{3}\right)$ given by

  $$W_{t}(\psi)=<W_{t}, \psi>=\frac{1}{4 \pi t} \int_{\|y\|=t} \psi(y) d \Sigma(y)$$

  for every Schwartz function $\psi \in \mathcal{S}\left(\mathbb{R}^{3}\right)$. Here $d \Sigma(y)=t^{2} d \Omega(y)$ is the integration element on the sphere of radius $t$.

  Hence deduce the formula of Kirchoff for the solution of the initial value problem for the wave equation in three space dimensions,

  $$\frac{\partial^{2} u}{\partial t^{2}}-\Delta u=0$$

  with initial data $u(0, x)=0$ and $\frac{\partial u}{\partial t}(0, x)=g(x), x \in \mathbb{R}^{3}$, where $g \in \mathcal{S}\left(\mathbb{R}^{3}\right)$. Explain briefly why the formula is also valid for arbitrary smooth $g \in C^{\infty}\left(\mathbb{R}^{3}\right)$.

  (iii) Show that any $C^{2}$ solution of the initial value problem in (ii) is given by the formula derived in (ii) (uniqueness).

  (iv) Show that any two $C^{2}$ solutions of the initial value problem for

  $$\frac{\partial^{2} u}{\partial t^{2}}+\frac{\partial u}{\partial t}-\Delta u=0$$

  with the same initial data as in (ii), also agree for any $t>0$.

  comment

• 1.II $. 30 \mathrm{~A}$

  Asymptotic Methods

  Part II, 2008

  Obtain an expression for the $n$th term of an asymptotic expansion, valid as $\lambda \rightarrow \infty$, for the integral

  $$I(\lambda)=\int_{0}^{1} t^{2 \alpha} e^{-\lambda\left(t^{2}+t^{3}\right)} d t \quad(\alpha>-1 / 2) .$$

  Estimate the value of $n$ for the term of least magnitude.

  Obtain the first two terms of an asymptotic expansion, valid as $\lambda \rightarrow \infty$, for the integral

  $$J(\lambda)=\int_{0}^{1} t^{2 \alpha} e^{-\lambda\left(t^{2}-t^{3}\right)} d t \quad(-1 / 2<\alpha<0)$$

  [Hint:

  $$\left.\Gamma(z)=\int_{0}^{\infty} t^{z-1} e^{-t} d t .\right]$$

  [Stirling's formula may be quoted.]

  comment

• 3.II $. 30 \mathrm{~A}$

  Asymptotic Methods

  Part II, 2008

  Describe how the leading-order approximation may be found by the method of stationary phase of

  $$I(\lambda)=\int_{a}^{b} f(t) \exp (i \lambda g(t)) d t$$

  for $\lambda \gg 1$, where $\lambda, f$ and $g$ are real. You should consider the cases for which: (a) $g^{\prime}(t)$ has one simple zero at $t=t_{0}$, where $a<t_{0}<b$; (b) $g^{\prime}(t)$ has more than one simple zero in the region $a<t<b$; and (c) $g^{\prime}(t)$ has only a simple zero at $t=b$.

  What is the order of magnitude of $I(\lambda)$ if $g^{\prime}(t)$ is non zero for $a \leqslant t \leqslant b$ ?

  Use the method of stationary phase to find the leading-order approximation for $\lambda \gg 1$ to

  $$J(\lambda)=\int_{0}^{1} \sin \left(\lambda\left(t^{3}-t\right)\right) d t$$

  [Hint:

  $$\left.\int_{-\infty}^{\infty} \exp \left(i u^{2}\right) d u=\sqrt{\pi} e^{i \pi / 4} .\right]$$

  comment

• 1.I.3G

  Geometry of Group Actions

  Part II, 2008

  Prove that an isometry of Euclidean space $\mathbb{R}^{3}$ is an affine transformation.

  Deduce that a finite group of isometries of $\mathbb{R}^{3}$ has a common fixed point.

  comment

• 4.II $. 31 \mathrm{~A}$

  Asymptotic Methods

  Part II, 2008

  The Bessel equation of order $n$ is

  $$z^{2} y^{\prime \prime}+z y^{\prime}+\left(z^{2}-n^{2}\right) y=0 .$$

  Here, $n$ is taken to be an integer, with $n \geqslant 0$. The transformation $w(z)=z^{\frac{1}{2}} y(z)$ converts (1) to the form

  $$w^{\prime \prime}+q(z) w=0$$

  where

  $$q(z)=1-\frac{\left(n^{2}-\frac{1}{4}\right)}{z^{2}}$$

  Find two linearly independent solutions of the form

  $$w=e^{s z} \sum_{k=0}^{\infty} c_{k} z^{\rho-k}$$

  where $c_{k}$ are constants, with $c_{0} \neq 0$, and $s$ and $\rho$ are to be determined. Find recurrence relationships for the $c_{k}$.

  Find the first two terms of two linearly independent Liouville-Green solutions of (2) for $w(z)$ valid in a neighbourhood of $z=\infty$. Relate these solutions to those of the form (3).

  comment

• 1.II.31C

  Integrable Systems

  Part II, 2008

  Define an integrable system in the context of Hamiltonian mechanics with a finite number of degrees of freedom and state the Arnold-Liouville theorem.

  Consider a six-dimensional phase space with its canonical coordinates $\left(p_{j}, q_{j}\right)$, $j=1,2,3$, and the Hamiltonian

  $$\frac{1}{2} \sum_{j=1}^{3} p_{j}^{2}+F(r)$$

  where $r=\sqrt{q_{1}^{2}+q_{2}^{2}+q_{3}^{2}}$ and where $F$ is an arbitrary function. Show that both $M_{1}=q_{2} p_{3}-q_{3} p_{2}$ and $M_{2}=q_{3} p_{1}-q_{1} p_{3}$ are first integrals.

  State the Jacobi identity and deduce that the Poisson bracket

  $$M_{3}=\left\{M_{1}, M_{2}\right\}$$

  is also a first integral. Construct a suitable expression out of $M_{1}, M_{2}, M_{3}$ to demonstrate that the system admits three first integrals in involution and thus satisfies the hypothesis of the Arnold-Liouville theorem.

  comment

• 2.II.31C

  Integrable Systems

  Part II, 2008

  Describe the inverse scattering transform for the $\mathrm{KdV}$ equation, paying particular attention to the Lax representation and the evolution of the scattering data.

  [Hint: you may find it helpful to consider the operator

  $$\left.A=4 \frac{d^{3}}{d x^{3}}-3\left(u \frac{d}{d x}+\frac{d}{d x} u\right) \cdot\right]$$

  comment

• 3.II.31C

  Integrable Systems

  Part II, 2008

  Let $U(\lambda)$ and $V(\lambda)$ be matrix-valued functions of $(x, y)$ depending on the auxiliary parameter $\lambda$. Consider a system of linear PDEs

  $$\frac{\partial}{\partial x} \Phi=U(\lambda) \Phi, \quad \frac{\partial}{\partial y} \Phi=V(\lambda) \Phi$$

  where $\Phi$ is a column vector whose components depend on $(x, y, \lambda)$. Derive the zero curvature representation as the compatibility conditions for this system.

  Assume that

  $$U(\lambda)=-\left(\begin{array}{ccc} u_{x} & 0 & \lambda \\ 1 & -u_{x} & 0 \\ 0 & 1 & 0 \end{array}\right), \quad V(\lambda)=-\left(\begin{array}{ccc} 0 & e^{-2 u} & 0 \\ 0 & 0 & e^{u} \\ \lambda^{-1} e^{u} & 0 & 0 \end{array}\right)$$

  and show that (1) is compatible if the function $u=u(x, y)$ satisfies the PDE

  $$\frac{\partial^{2} u}{\partial x \partial y}=F(u)$$

  for some $F(u)$ which should be determined.

  Show that the transformation

  $$(x, y) \longrightarrow\left(c x, c^{-1} y\right), \quad c \in \mathbb{R} \backslash\{0\}$$

  forms a symmetry group of the PDE (2) and find the vector field generating this group.

  Find the ODE characterising the group-invariant solutions of (2).

  comment

• 1.II.32D

  Principles of Quantum Mechanics

  Part II, 2008

  (a) If $A$ and $B$ are operators which each commute with their commutator $[A, B]$, show that $\left[A, e^{B}\right]=[A, B] e^{B}$. By considering

  $$F(\lambda)=e^{\lambda A} e^{\lambda B} e^{-\lambda(A+B)}$$

  and differentiating with respect to the parameter $\lambda$, show also that

  $$e^{A} e^{B}=C e^{A+B}=e^{A+B} C$$

  where $C=e^{\frac{1}{2}[A, B]}$.

  (b) Consider a one-dimensional quantum system with position $\hat{x}$ and momentum $\hat{p}$. Write down a formula for the operator $U(\alpha)$ corresponding to translation through $\alpha$, calculate $[\hat{x}, U(\alpha)]$, and show that your answer is consistent with the assumption that position eigenstates obey $|x+\alpha\rangle=U(\alpha)|x\rangle$. Given this assumption, express the wavefunction for $U(\alpha)|\psi\rangle$ in terms of the wavefunction $\psi(x)$ for $|\psi\rangle$.

  Now suppose the one-dimensional system is a harmonic oscillator of mass $m$ and frequency $\omega$. Show that

  $$\psi_{0}(x-\alpha)=e^{-m \omega \alpha^{2} / 4 \hbar} \sum_{n=0}^{\infty}\left(\frac{m \omega}{2 \hbar}\right)^{n / 2} \frac{\alpha^{n}}{\sqrt{n !}} \psi_{n}(x),$$

  where $\psi_{n}(x)$ are normalised wavefunctions with energies $E_{n}=\hbar \omega\left(n+\frac{1}{2}\right)$.

  [Standard results for constructing normalised energy eigenstates in terms of annihilation and creation operators

  $$a=\left(\frac{m \omega}{2 \hbar}\right)^{1 / 2}\left(\hat{x}+\frac{i}{m \omega} \hat{p}\right), \quad a^{\dagger}=\left(\frac{m \omega}{2 \hbar}\right)^{1 / 2}\left(\hat{x}-\frac{i}{m \omega} \hat{p}\right)$$

  may be quoted without proof.]

  comment

• 2.II.32D

  Principles of Quantum Mechanics

  Part II, 2008

  Derive approximate expressions for the eigenvalues of a Hamiltonian $H+\lambda V$, working to second order in the parameter $\lambda$ and assuming the eigenstates and eigenvalues of $H$ are known and non-degenerate.

  Let $\mathbf{J}=\left(J_{1}, J_{2}, J_{3}\right)$ be angular momentum operators with $|j m\rangle$ joint eigenstates of $\mathbf{J}^{2}$ and $J_{3}$. What are the possible values of the labels $j$ and $m$ and what are the corresponding eigenvalues of the operators?

  A particle with spin $j$ is trapped in space (its position and momentum can be ignored) but is subject to a magnetic field of the form $\mathbf{B}=\left(B_{1}, 0, B_{3}\right)$, resulting in a Hamiltonian $-\gamma\left(B_{1} J_{1}+B_{3} J_{3}\right)$. Starting from the eigenstates and eigenvalues of this Hamiltonian when $B_{1}=0$, use perturbation theory to compute the leading order corrections to the energies when $B_{1}$ is non-zero but much smaller than $B_{3}$. Compare with the exact result.

  [You may set $\hbar=1$ and use $J_{\pm}|j m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j m \pm 1\rangle .$ ]

  comment

• 3.II $32 \mathrm{D}$

  Principles of Quantum Mechanics

  Part II, 2008

  Explain, in a few lines, how the Pauli matrices $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ with

  $$\sigma_{1}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  are used to represent angular momentum operators with respect to basis states $|\uparrow\rangle$ and $|\downarrow\rangle$ corresponding to spin up and spin down along the 3 -axis. You should state clearly which properties of the matrices correspond to general features of angular momentum and which are specific to spin half.

  Consider two spin-half particles labelled A and B, each with its spin operators and spin eigenstates. Find the matrix representation of

  $$\boldsymbol{\sigma}^{(\mathrm{A})} \cdot \boldsymbol{\sigma}^{(\mathrm{B})}=\sigma_{1}^{(\mathrm{A})} \sigma_{1}^{(\mathrm{B})}+\sigma_{2}^{(\mathrm{A})} \sigma_{2}^{(\mathrm{B})}+\sigma_{3}^{(\mathrm{A})} \sigma_{3}^{(\mathrm{B})}$$

  with respect to a basis of two-particle states $|\uparrow\rangle_{\mathrm{A}}|\uparrow\rangle_{\mathrm{B}},|\downarrow\rangle_{\mathrm{A}}|\uparrow\rangle_{\mathrm{B}},|\uparrow\rangle_{\mathrm{A}}|\downarrow\rangle_{\mathrm{B}},|\downarrow\rangle_{\mathrm{A}}|\downarrow\rangle_{\mathrm{B}}$. Show that the eigenvalues of the matrix are $1,1,1,-3$ and find the eigenvectors.

  What is the behaviour of each eigenvector under interchange of $\mathrm{A}$ and $\mathrm{B}$ ? If the particles are identical, and there are no other relevant degrees of freedom, which of the two-particle states are allowed?

  By relating $\left(\boldsymbol{\sigma}^{(\mathrm{A})}+\boldsymbol{\sigma}^{(\mathrm{B})}\right)^{2}$ to the operator discussed above, show that your findings are consistent with standard results for addition of angular momentum.

  comment

• 4.II.32D

  Principles of Quantum Mechanics

  Part II, 2008

  Define the interaction picture for a quantum mechanical system with Schrödinger picture Hamiltonian $H_{0}+V(t)$ and explain why either picture gives the same physical predictions. Derive an equation of motion for interaction picture states and use this to show that the probability of a transition from a state $|n\rangle$ at time zero to a state $|m\rangle$ at time $t$ is

  $$P(t)=\frac{1}{\hbar^{2}}\left|\int_{0}^{t} e^{i\left(E_{m}-E_{n}\right) t^{\prime} / \hbar}\left\langle m\left|V\left(t^{\prime}\right)\right| n\right\rangle d t^{\prime}\right|^{2}$$

  correct to second order in $V$, where the initial and final states are orthogonal eigenstates of $H_{0}$ with eigenvalues $E_{n}$ and $E_{m}$.

  Consider a perturbed harmonic oscillator:

  $$H_{0}=\hbar \omega\left(a^{\dagger} a+\frac{1}{2}\right), \quad V(t)=\hbar \lambda\left(a e^{i \nu t}+a^{\dagger} e^{-i \nu t}\right)$$

  with $a$ and $a^{\dagger}$ annihilation and creation operators (all usual properties may be assumed). Working to order $\lambda^{2}$, find the probability for a transition from an initial state with $E_{n}=\hbar \omega\left(n+\frac{1}{2}\right)$ to a final state with $E_{m}=\hbar \omega\left(m+\frac{1}{2}\right)$ after time $t$.

  Suppose $t$ becomes large and perturbation theory still applies. Explain why the rate $P(t) / t$ for each allowed transition is sharply peaked, as a function of $\nu$, around $\nu=\omega$.

  comment

• 1.II.33E

  Applications of Quantum Mechanics

  Part II, 2008

  A beam of particles each of mass $m$ and energy $\hbar^{2} k^{2} /(2 m)$ scatters off an axisymmetric potential $V$. In the first Born approximation the scattering amplitude is

  $$f(\theta)=-\frac{m}{2 \pi \hbar^{2}} \int e^{-i\left(\mathbf{k}-\mathbf{k}_{0}\right) \cdot \mathbf{x}^{\prime}} V\left(\mathbf{x}^{\prime}\right) d^{3} x^{\prime}$$

  where $\mathbf{k}_{0}=(0,0, k)$ is the wave vector of the incident particles and $\mathbf{k}=(k \sin \theta, 0, k \cos \theta)$ is the wave vector of the outgoing particles at scattering angle $\theta$ (and $\phi=0$ ). Let $\mathbf{q}=\mathbf{k}-\mathbf{k}_{0}$ and $q=|\mathbf{q}|$. Show that when the scattering potential $V$ is spherically symmetric the expression $(*)$ simplifies to

  $$f(\theta)=-\frac{2 m}{\hbar^{2} q} \int_{0}^{\infty} r^{\prime} V\left(r^{\prime}\right) \sin \left(q r^{\prime}\right) d r^{\prime}$$

  and find the relation between $q$ and $\theta$.

  Calculate this scattering amplitude for the potential $V(r)=V_{0} e^{-r}$ where $V_{0}$ is a constant, and show that at high energies the particles emerge predominantly in a narrow cone around the forward beam direction. Estimate the angular width of the cone.

  comment

• 2.II.33E

  Applications of Quantum Mechanics

  Part II, 2008

  Consider a large, essentially two-dimensional, rectangular sample of conductor of area $A$, and containing $2 N$ electrons of charge $-e$. Suppose a magnetic field of strength $B$ is applied perpendicularly to the sample. Write down the Landau Hamiltonian for one of the electrons assuming that the electron interacts just with the magnetic field.

  [You may ignore the interaction of the electron spin with the magnetic field.]

  Find the allowed energy levels of the electron.

  Find the total energy of the $2 N$ electrons at absolute zero temperature as a function of $B$, assuming that $B$ is in the range

  $$\frac{\pi \hbar N}{e A} \leqslant B \leqslant \frac{2 \pi \hbar N}{e A} .$$

  Comment on the values of the total energy when $B$ takes the values at the two ends of this range.

  comment

• 1.II.11G

  Geometry of Group Actions

  Part II, 2008

  What is meant by an inversion in a circle in $\mathbb{C} \cup\{\infty\}$ ? Show that a composition of two inversions is a Möbius transformation.

  Hence, or otherwise, show that if $C^{+}$and $C^{-}$are two disjoint circles in $\mathbb{C}$, then the composition of the inversions in $C^{+}$and $C^{-}$has two fixed points.

  comment

• 3.II.33E

  Applications of Quantum Mechanics

  Part II, 2008

  Consider the body-centred cuboidal lattice $L$ with lattice points $\left(n_{1} a, n_{2} a, n_{3} b\right)$ and $\left(\left(n_{1}+\frac{1}{2}\right) a,\left(n_{2}+\frac{1}{2}\right) a,\left(n_{3}+\frac{1}{2}\right) b\right)$, where $a$ and $b$ are positive and $n_{1}, n_{2}$ and $n_{3}$ take all possible integer values. Find the reciprocal lattice $\widetilde{L}$and describe its geometrical form. Calculate the volumes of the unit cells of the lattices $L$ and $\widetilde{L}$.

  Find the reciprocal lattice vector associated with the lattice planes parallel to the plane containing the points $(0,0, b),(0, a, b),\left(\frac{1}{2} a, \frac{1}{2} a, \frac{1}{2} b\right),(a, 0,0)$ and $(a, a, 0)$. Deduce the allowed Bragg scattering angles of X-rays off these planes, assuming that $b=\frac{4}{3} a$ and that the X-rays have wavelength $\lambda=\frac{1}{2} a$.

  comment

• 4.II.33E

  Applications of Quantum Mechanics

  Part II, 2008

  Explain why the allowed energies of electrons in a three-dimensional crystal lie in energy bands. What quantum numbers can be used to classify the electron energy eigenstates?

  Describe the effect on the energy level structure of adding a small density of impurity atoms randomly to the crystal.

  comment

• $2 . \mathrm{II} . 34 \mathrm{E} \quad$

  Statistical Physics

  Part II, 2008

  Prove that energy fluctuations in a canonical distribution are given by

  $$\left\langle(E-\langle E\rangle)^{2}\right\rangle=k_{B} T^{2} C_{V}$$

  where $T$ is the absolute temperature, $C_{V}=\left.\frac{\partial\langle E\rangle}{\partial T}\right|_{V}$ is the heat capacity at constant volume, and $k_{B}$ is Boltzmann's constant.

  Prove the following relation in a similar manner:

  $$\left\langle(E-\langle E\rangle)^{3}\right\rangle=k_{B}^{2}\left[\left.T^{4} \frac{\partial C_{V}}{\partial T}\right|_{V}+2 T^{3} C_{V}\right]$$

  Show that, for an ideal gas of $N$ monatomic molecules where $\langle E\rangle=\frac{3}{2} N k_{B} T$, these equations can be reduced to

  $$\frac{1}{\langle E\rangle^{2}}\left\langle(E-\langle E\rangle)^{2}\right\rangle=\frac{2}{3 N} \quad \text { and } \quad \frac{1}{\langle E\rangle^{3}}\left\langle(E-\langle E\rangle)^{3}\right\rangle=\frac{8}{9 N^{2}}$$

  comment

• 3.II.34E

  Statistical Physics

  Part II, 2008

  Derive the following two relations:

  $$T d S=C_{p} d T-\left.T \frac{\partial V}{\partial T}\right|_{p} d p$$

  and

  $$T d S=C_{V} d T+\left.T \frac{\partial p}{\partial T}\right|_{V} d V$$

  [You may use any standard Maxwell relation without proving it.]

  Experimentalists very seldom measure $C_{V}$ directly; they measure $C_{p}$ and use thermodynamics to extract $C_{V}$. Use your results from the first part of this question to find a formula for $C_{p}-C_{V}$ in terms of the easily measured quantities

  $$\alpha=\left.\frac{1}{V} \frac{\partial V}{\partial T}\right|_{p}$$

  (the volume coefficient of expansion) and

  $$\kappa=-\left.\frac{1}{V} \frac{\partial V}{\partial p}\right|_{T}$$

  (the isothermal compressibility).

  comment

• 4.II.34D

  Statistical Physics

  Part II, 2008

  Show that the Fermi momentum $p_{F}$ of a gas of $N$ non-interacting electrons in volume $V$ is

  $$p_{F}=\left(3 \pi^{2} \hbar^{3} \frac{N}{V}\right)^{1 / 3}$$

  Consider the electrons to be effectively massless, so that an electron of momentum $p$ has (relativistic) energy $c p$. Show that the mean energy per electron at zero temperature is $3 c p_{F} / 4$.

  When a constant external magnetic field of strength $B$ is applied to the electron gas, each electron gets an energy contribution $\pm \mu B$ depending on whether its spin is parallel or antiparallel to the field. Here $\mu$ is the magnitude of the magnetic moment of an electron. Calculate the total magnetic moment of the electron gas at zero temperature, assuming $\mu B$ is much less than $c p_{F}$.

  comment

• 1.II $. 34 \mathrm{D} \quad$

  Electrodynamics

  Part II, 2008

  Frame $\mathcal{S}^{\prime}$ is moving with uniform speed $v$ in the $x$-direction relative to a laboratory frame $\mathcal{S}$. The components of the electric and magnetic fields $\mathbf{E}$ and $\mathbf{B}$ in the two frames are related by the Lorentz transformation

  where $\gamma=1 / \sqrt{1-v^{2}}$ and units are chosen so that $c=1$. How do the components of the spatial vector $\mathbf{F}=\mathbf{E}+i \mathbf{B}$ (where $i=\sqrt{-1}$ ) transform?

  Show that $\mathbf{F}^{\prime}$ is obtained from $\mathbf{F}$ by a rotation through $\theta$ about a spatial axis $\mathbf{n}$, where $\mathbf{n}$ and $\theta$ should be determined. Hence, or otherwise, show that there are precisely two independent scalars associated with $\mathbf{F}$ which are preserved by the Lorentz transformation, and obtain them.

  [Hint: since $|v|<1$ there exists a unique real $\psi$ such that $v=\tanh \psi$.]

  comment

• $3 . \mathrm{II} . 35 \mathrm{D} \quad$

  Electrodynamics

  Part II, 2008

  The retarded scalar potential $\varphi(t, \mathbf{x})$ produced by a charge distribution $\rho(t, \mathbf{x})$ is given by

  $$\varphi(t, \mathbf{x})=\frac{1}{4 \pi \epsilon_{0}} \int_{\Omega} d^{3} x^{\prime} \frac{\rho\left(t-\left|\mathbf{x}-\mathbf{x}^{\prime}\right|, \mathbf{x}^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|}$$

  where $\Omega$ denotes all 3 -space. Describe briefly and qualitatively the physics underlying this formula.

  Write the integrand in the formula above as a 1-dimensional integral over a new time coordinate $\tau$. Next consider a special source, a point charge $q$ moving along a trajectory $\mathbf{x}=\mathbf{x}_{0}(t)$ so that

  $$\rho(t, \mathbf{x})=q \delta^{(3)}\left(\mathbf{x}-\mathbf{x}_{0}(t)\right),$$

  where $\delta^{(3)}(\mathbf{x})$ denotes the 3 -dimensional delta function. By reversing the order of integration, or otherwise, obtain the Liénard-Wiechert potential

  $$\varphi(t, \mathbf{x})=\frac{1}{4 \pi \epsilon_{0}} \frac{q}{R-\mathbf{v} \cdot \mathbf{R}},$$

  where $\mathbf{v}$ and $\mathbf{R}$ are to be determined.

  Write down the corresponding formula for the vector potential $\mathbf{A}(t, \mathbf{x})$.

  $$\begin{aligned} & E_{x}^{\prime}=E_{x}, \quad E_{y}^{\prime}=\gamma\left(E_{y}-v B_{z}\right), \quad E_{z}^{\prime}=\gamma\left(E_{z}+v B_{y}\right), \\ & B_{x}^{\prime}=B_{x}, \quad B_{y}^{\prime}=\gamma\left(B_{y}+v E_{z}\right), \quad B_{z}^{\prime}=\gamma\left(B_{z}-v E_{y}\right), \end{aligned}$$

  comment

• 4.II $. 35 \mathrm{D} \quad$

  Electrodynamics

  Part II, 2008

  The Maxwell field tensor is given by

  $$F^{a b}=\left(\begin{array}{cccc} 0 & -E_{x} & -E_{y} & -E_{z} \\ E_{x} & 0 & -B_{z} & B_{y} \\ E_{y} & B_{z} & 0 & -B_{x} \\ E_{z} & -B_{y} & B_{x} & 0 \end{array}\right)$$

  A general 4-velocity is written as $U^{a}=\gamma(1, \mathbf{v})$, where $\gamma=\left(1-|\mathbf{v}|^{2}\right)^{-1 / 2}$, and $c=1$. A general 4-current density is written as $J^{a}=(\rho, \mathbf{j})$, where $\rho$ is the charge density and $\mathbf{j}$ is the 3 -current density. Show that

  $$F^{a b} U_{b}=\gamma(\mathbf{E} \cdot \mathbf{v}, \mathbf{E}+\mathbf{v} \times \mathbf{B})$$

  In the rest frame of a conducting medium, Ohm's law states that $\mathbf{j}=\sigma \mathbf{E}$ where $\sigma$ is the conductivity. Show that the relativistic generalization to a frame in which the medium moves with uniform velocity $\mathbf{v}$ is

  $$J^{a}-\left(J^{b} U_{b}\right) U^{a}=\sigma F^{a b} U_{b}$$

  Show that this implies

  $$\mathbf{j}=\rho \mathbf{v}+\sigma \gamma(\mathbf{E}+\mathbf{v} \times \mathbf{B}-(\mathbf{v} \cdot \mathbf{E}) \mathbf{v})$$

  Simplify this formula, given that the charge density vanishes in the rest frame of the medium

  comment

• 1.II.35E

  General Relativity

  Part II, 2008

  For the metric

  $$\mathrm{d} s^{2}=\frac{1}{r^{2}}\left(-\mathrm{d} t^{2}+\mathrm{d} r^{2}\right), \quad r \geqslant 0,$$

  obtain the geodesic equations of motion. For a massive particle show that

  $$\left(\frac{\mathrm{d} r}{\mathrm{~d} t}\right)^{2}=1-\frac{1}{k^{2} r^{2}}$$

  for some constant $k$. Show that the particle moves on trajectories

  $$r^{2}-t^{2}=\frac{1}{k^{2}}, \quad k r=\sec \tau, \quad k t=\tan \tau$$

  where $\tau$ is the proper time, if the origins of $t, \tau$ are chosen appropriately.

  comment

• 2.II.35E

  General Relativity

  Part II, 2008

  Let $x^{a}(\lambda)$ be a path $P$ with tangent vector $T^{a}=\frac{d}{d \lambda} x^{a}(\lambda)$. For vectors $X^{a}(x(\lambda))$ and $Y^{a}(x(\lambda))$ defined on $P$ let

  $$\nabla_{T} X^{a}=\frac{d}{d \lambda} X^{a}+\Gamma_{b c}^{a}(x(\lambda)) X^{b} T^{c}$$

  where $\Gamma_{b c}^{a}(x)$ is the metric connection for a metric $g_{a b}(x) . \nabla_{T} Y^{a}$ is defined similarly. Suppose $P$ is geodesic and $\lambda$ is an affine parameter. Explain why $\nabla_{T} T^{a}=0$. Show that if $\nabla_{T} X^{a}=\nabla_{T} Y^{a}=0$ then $g_{a b}(x(\lambda)) X^{a}(x(\lambda)) Y^{b}(x(\lambda))$ is constant along $P$.

  If $x^{a}(\lambda, \mu)$ is a family of geodesics which depend on $\mu$, let $S^{a}=\frac{\partial}{\partial \mu} x^{a}$ and define

  $$\nabla_{S} X^{a}=\frac{\partial}{\partial \mu} X^{a}+\Gamma_{b c}^{a}(x(\lambda)) X^{b} S^{c}$$

  Show that $\nabla_{T} S^{a}=\nabla_{S} T^{a}$ and obtain

  $$\nabla_{T}{ }^{2} S^{a} \equiv \nabla_{T}\left(\nabla_{T} S^{a}\right)=R_{b c d}^{a} T^{b} T^{c} S^{d}$$

  What is the physical relevance of this equation in general relativity? Describe briefly how this is relevant for an observer moving under gravity.

  [You may assume $\left[\nabla_{T}, \nabla_{S}\right] X^{a}=R_{b c d}^{a} X^{b} T^{c} S^{d}$.]

  comment

• 2.I.3G

  Geometry of Group Actions

  Part II, 2008

  State a theorem classifying lattices in $\mathbb{R}^{2}$. Define a frieze group.

  Show there is a frieze group which is isomorphic to $\mathbb{Z}$ but is not generated by a translation, and draw a picture whose symmetries are this group.

  comment

• 4.II.36E

  General Relativity

  Part II, 2008

  A solution of the Einstein equations is given by the metric

  $$\mathrm{d} s^{2}=-\left(1-\frac{2 M}{r}\right) \mathrm{d} t^{2}+\frac{1}{\left(1-\frac{2 M}{r}\right)} \mathrm{d} r^{2}+r^{2}\left(\mathrm{~d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right)$$

  For an incoming light ray, with constant $\theta, \phi$, show that

  $$t=v-r-2 M \log \left|\frac{r}{2 M}-1\right|,$$

  for some fixed $v$ and find a similar solution for an outgoing light ray. For the outgoing case, assuming $r>2 M$, show that in the far past $\frac{r}{2 M}-1 \propto \exp \left(\frac{t}{2 M}\right)$ and in the far future $r \sim t$.

  Obtain the transformed metric after the change of variables $(t, r, \theta, \phi) \rightarrow(v, r, \theta, \phi)$. With coordinates $\hat{t}=v-r, r$ sketch, for fixed $\theta, \phi$, the trajectories followed by light rays. What is the significance of the line $r=2 M$ ?

  Show that, whatever path an observer with initial $r=r_{0}<2 M$ takes, he must reach $r=0$ in a finite proper time.

  comment

• 1.II.36A

  Fluid Dynamics II

  Part II, 2008

  Derive the relation between the stress tensor $\sigma_{i j}$ and the rate-of-strain tensor $e_{i j}$ in an incompressible Newtonian fluid, using the result that there is a linear dependence between the components of $\sigma_{i j}$ and those of $e_{i j}$ that is the same in all frames. Write down the boundary conditions that hold at an interface between two viscous fluids.

  Viscous fluid is contained in a channel between the rigid planes $y=-a$ and $y=a$. The fluid in $y<0$ has dynamic viscosity $\mu_{-}$, while that in $y>0$ has dynamic viscosity $\mu_{+}$. Gravity may be neglected. The fluids move through the channel in the $x$-direction under the influence of a pressure gradient applied at the ends of the channel. It may be assumed that the velocity has no $z$-components, and all quantities are independent of $z$.

  Find a steady solution of the Navier-Stokes equation in which the interface between the two fluids remains at $y=0$, the fluid velocity is everywhere independent of $x$, and the pressure gradient is uniform. Use it to calculate the following:

  (a) the viscous tangential stress at $y=-a$ and at $y=a$; and

  (b) the ratio of the volume fluxes of the two different fluids.

  Comment on the limits of each of the results in (a) and (b) as $\mu_{+} / \mu_{-} \rightarrow 1$, and as $\mu_{+} / \mu_{-} \rightarrow \infty$

  comment

• 2.II.36A

  Fluid Dynamics II

  Part II, 2008

  Viscous fluid with dynamic viscosity $\mu$ flows with velocity $\left(u_{x}, u_{y}, u_{z}\right) \equiv\left(\mathbf{u}_{H}, u_{z}\right)$ (in cartesian coordinates $x, y, z)$ in a shallow container with a free surface at $z=0$. The base of the container is rigid, and is at $z=-h(x, y)$. A horizontal stress $\mathbf{S}(x, y)$ is applied at the free surface. Gravity may be neglected.

  Using lubrication theory (conditions for the validity of which should be clearly stated), show that the horizontal volume flux $\mathbf{q}(x, y) \equiv \int_{-h}^{0} \mathbf{u}_{H} d z$ satisfies the equations

  $$\nabla \cdot \mathbf{q}=0, \quad \mu \mathbf{q}=-\frac{1}{3} h^{3} \nabla p+\frac{1}{2} h^{2} \mathbf{S}$$

  where $p(x, y)$ is the pressure. Find also an expression for the surface velocity $\mathbf{u}_{0}(x, y) \equiv$ $\mathbf{u}_{H}(x, y, 0)$ in terms of $\mathbf{S}, \mathbf{q}$ and $h$.

  Now suppose that the container is cylindrical with boundary at $x^{2}+y^{2}=a^{2}$, where $a \gg h$, and that the surface stress is uniform and in the $x$-direction, so $\mathbf{S}=\left(S_{0}, 0\right)$ with $S_{0}$ constant. It can be assumed that the correct boundary condition to apply at $x^{2}+y^{2}=a^{2}$ is $\mathbf{q} \cdot \mathbf{n}=0$, where $\mathbf{n}$ is the unit normal.

  Write $\mathbf{q}=\nabla \psi(x, y) \times \hat{\mathbf{z}}$, and show that $\psi$ satisfies the equation

  $$\nabla \cdot\left(\frac{1}{h^{3}} \nabla \psi\right)=-\frac{S_{0}}{2 \mu h^{2}} \frac{\partial h}{\partial y}$$

  Deduce that if $h=h_{0}$ (constant) then $\mathbf{q}=\mathbf{0}$. Find $\mathbf{u}_{\mathbf{0}}$ in this case.

  Now suppose that $h=h_{0}(1+\epsilon y / a)$, where $\epsilon \ll 1$. Verify that to leading order in $\epsilon, \psi=\epsilon C\left(x^{2}+y^{2}-a^{2}\right)$ for some constant $C$ to be determined. Hence determine $\mathbf{u}_{0}$ up to and including terms of order $\epsilon$.

  [Hint: $\nabla \times(\mathbf{A} \times \hat{\mathbf{z}})=\hat{\mathbf{z}} \cdot \nabla \mathbf{A}-\hat{\mathbf{z}} \nabla \cdot \mathbf{A}$ for any vector field $\mathbf{A} .]$

  comment

• 3.II.36A

  Fluid Dynamics II

  Part II, 2008

  Show that, in cylindrical polar co-ordinates, the streamfunction $\psi(r, \phi)$ for the velocity $\mathbf{u}=\left(u_{r}(r, \phi), u_{\phi}(r, \phi), 0\right)$ and vorticity $(0,0, \omega(r, \phi))$ of two-dimensional Stokes flow of incompressible fluid satisfies the equations

  $$\mathbf{u}=\left(\frac{1}{r} \frac{\partial \psi}{\partial \phi},-\frac{\partial \psi}{\partial r}, 0\right), \quad \nabla^{2} \omega=-\nabla^{4} \psi=0$$

  Show also that the pressure $p(r, \phi)$ satisfies $\nabla^{2} p=0$.

  A stationary rigid circular cylinder of radius $a$ occupies the region $r \leqslant a$. The flow around the cylinder tends at large distances to a simple shear flow, with velocity given in cartesian coordinates $(x, y, z)$ by $\mathbf{u}=(\Gamma y, 0,0)$. Inertial forces may be neglected.

  By solving the equation for $\psi$ in cylindrical polars, determine the flow field everywhere. Determine the torque on the cylinder per unit length in $z$.

  [Hint: in cylindrical polars

  $$\nabla^{2} V=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial V}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} V}{\partial \phi^{2}}$$

  The off-diagonal component of the rate-of-strain tensor is given by

  $$\left.e_{r \phi}=\frac{1}{2}\left(\frac{1}{r} \frac{\partial u_{r}}{\partial \phi}+r \frac{\partial}{\partial r}\left(\frac{u_{\phi}}{r}\right)\right) .\right]$$

  comment

• 4.II.37A

  Fluid Dynamics II

  Part II, 2008

  Viscous incompressible fluid of uniform density is extruded axisymmetrically from a thin circular slit of small radius centred at the origin and lying in the plane $z=0$ in cylindrical polar coordinates $r, \theta, z$. There is no external radial pressure gradient. It is assumed that the fluid forms a thin boundary layer, close to and symmetric about the plane $z=0$. The layer has thickness $\delta(r) \ll r$. The $r$-component of the steady Navier-Stokes equations may be approximated by

  $$u_{r} \frac{\partial u_{r}}{\partial r}+u_{z} \frac{\partial u_{r}}{\partial z}=\nu \frac{\partial^{2} u_{r}}{\partial z^{2}}$$

  (i) Prove that the quantity (proportional to the flux of radial momentum)

  $$\mathcal{F}=\int_{-\infty}^{\infty} u_{r}^{2} r d z$$

  is independent of $r$.

  (ii) Show, by balancing terms in the momentum equation and assuming constancy of $\mathcal{F}$, that there is a similarity solution of the form

  $$u_{r}=-\frac{1}{r} \frac{\partial \Psi}{\partial z}, \quad u_{z}=\frac{1}{r} \frac{\partial \Psi}{\partial r}, \quad \Psi=-A \delta(r) f(\eta), \quad \eta=\frac{z}{\delta(r)}, \quad \delta(r)=C r$$

  where $A, C$ are constants. Show that for suitable choices of $A$ and $C$ the equation for $f$ takes the form

  $$\begin{gathered} -f^{\prime 2}-f f^{\prime \prime}=f^{\prime \prime \prime} ; \\ f=f^{\prime \prime}=0 \text { at } \eta=0 ; \quad f^{\prime} \rightarrow 0 \text { as } \eta \rightarrow \infty ; \\ \int_{-\infty}^{\infty} f_{\eta}^{2} d \eta=1 . \end{gathered}$$

  (iii) Give an inequality connecting $\mathcal{F}$ and $\nu$ that ensures that the boundary layer approximation $(\delta \ll r)$ is valid. Solve the equation to give a complete solution to the problem for $u_{r}$ when this inequality holds.

  [Hint: $\left.\int_{-\infty}^{\infty} \operatorname{sech}^{4} x d x=4 / 3 .\right]$

  comment

• 1.II $. 37 \mathrm{~B}$

  Waves

  Part II, 2008

  Show that in an acoustic plane wave the velocity and perturbation pressure are everywhere proportional and find the constant of proportionality.

  Gas occupies a tube lying parallel to the $x$-axis. In the regions $x<0$ and $x>L$ the gas has uniform density $\rho_{0}$ and sound speed $c_{0}$. For $0<x<L$ the gas is cooled so that it has uniform density $\rho_{1}$ and sound speed $c_{1}$. A harmonic plane wave with frequency $\omega$ is incident from $x=-\infty$. Show that the amplitude of the wave transmitted into $x>L$ relative to that of the incident wave is

  $$|T|=\left[\cos ^{2} k_{1} L+\frac{1}{4}\left(\lambda+\lambda^{-1}\right)^{2} \sin ^{2} k_{1} L\right]^{-1 / 2}$$

  where $\lambda=\rho_{1} c_{1} / \rho_{0} c_{0}$ and $k_{1}=\omega / c_{1}$.

  What are the implications of this result if $\lambda \gg 1$ ?

  comment

• 2.II.37B

  Waves

  Part II, 2008

  Show that, in one-dimensional flow of a perfect gas at constant entropy, the Riemann invariants $u \pm 2\left(c-c_{0}\right) /(\gamma-1)$ are constant along characteristics $d x / d t=u \pm c$.

  A perfect gas occupies a tube that lies parallel to the $x$-axis. The gas is initially at rest and is in $x>0$. For times $t>0$ a piston is pulled out of the gas so that its position at time $t$ is

  $$x=X(t)=-\frac{1}{2} f t^{2}$$

  where $f>0$ is a constant. Sketch the characteristics of the resulting motion in the $(x, t)$ plane and explain why no shock forms in the gas.

  Calculate the pressure exerted by the gas on the piston for times $t>0$, and show that at a finite time $t_{v}$ a vacuum forms. What is the speed of the piston at $t=t_{v}$ ?

  comment

• 3.II $. 37 \mathrm{~B} \quad$

  Waves

  Part II, 2008

  The real function $\phi(x, t)$ satisfies the Klein-Gordon equation

  $$\frac{\partial^{2} \phi}{\partial t^{2}}=\frac{\partial^{2} \phi}{\partial x^{2}}-\phi, \quad-\infty<x<\infty, t \geqslant 0$$

  Find the dispersion relation for disturbances of wavenumber $k$ and deduce their phase and group velocities.

  Suppose that at $t=0$

  $$\phi(x, 0)=0 \quad \text { and } \quad \frac{\partial \phi}{\partial t}(x, 0)=e^{-|x|}$$

  Use Fourier transforms to find an integral expression for $\phi(x, t)$ when $t>0$.

  Use the method of stationary phase to find $\phi(V t, t)$ for $t \rightarrow \infty$ for fixed $0<V<1$. What can be said if $V>1$ ?

  [Hint: you may assume that

  $$\left.\int_{-\infty}^{\infty} e^{-a x^{2}} d x=\sqrt{\frac{\pi}{a}}, \quad \operatorname{Re}(a)>0 .\right]$$

  comment

• 4.II $. 38$ B

  Waves

  Part II, 2008

  A layer of rock of shear modulus $\bar{\mu}$ and shear wave speed $\bar{c}_{s}$ occupies the region $0 \leqslant y \leqslant h$ with a free surface at $y=h$. A second rock having shear modulus $\mu$ and shear wave speed $c_{s}>\bar{c}_{s}$ occupies $y \leqslant 0$. Show that elastic $S H$ waves of wavenumber $k$ and phase speed $c$ can propagate in the layer with zero disturbance at $y=-\infty$ if $\bar{c}_{s}<c<c_{s}$ and $c$ satisfies the dispersion relation

  $$\tan \left[k h \sqrt{c^{2} / \bar{c}_{s}^{2}-1}\right]=\frac{\mu}{\bar{\mu}} \frac{\sqrt{1-c^{2} / c_{s}^{2}}}{\sqrt{c^{2} / \bar{c}_{s}^{2}-1}} .$$

  Show graphically, or otherwise, that this equation has at least one real solution for any value of $k h$, and determine the smallest value of $k h$ for which the equation has at least two real solutions.

  comment

• 1.II.38C

  Numerical Analysis

  Part II, 2008

  The Poisson equation $\nabla^{2} u=f$ in the unit square $\Omega=[0,1] \times[0,1]$, with zero boundary conditions on $\partial \Omega$, is discretized with the nine-point formula

  $$\begin{aligned} \frac{10}{3} u_{m, n} &-\frac{2}{3}\left(u_{m+1, n}+u_{m-1, n}+u_{m, n+1}+u_{m, n-1}\right) \\ &-\frac{1}{6}\left(u_{m+1, n+1}+u_{m+1, n-1}+u_{m-1, n+1}+u_{m-1, n-1}\right)=-h^{2} f_{m, n}, \end{aligned}$$

  where $1 \leqslant m, n \leqslant M, u_{m, n} \approx u(m h, n h)$, and $(m h, n h)$ are grid points.

  (a) Prove that, for any ordering of the grid points, the method can be written as $A \mathbf{u}=\mathbf{b}$ with a symmetric positive-definite matrix $A$.

  (b) Describe the Jacobi method for solving a linear system of equations, and prove that it converges for the above system.

  [You may quote without proof the corollary of the Householder-John theorem regarding convergence of the Jacobi method.]

  comment

• 3.I.3G

  Geometry of Group Actions

  Part II, 2008

  Let $\operatorname{dim}_{H}$ denote the Hausdorff dimension of a set in $\mathbb{R}^{n}$. Prove that if $\operatorname{dim}_{H}(F)<1$ then $F$ is totally disconnected.

  [You may assume that if $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ is a Lipschitz map then

  $$\left.\operatorname{dim}_{H}(f(F)) \leqslant \operatorname{dim}_{H}(F) .\right]$$

  comment

• 2.II.38C

  Numerical Analysis

  Part II, 2008

  The advection equation

  $$u_{t}=u_{x}, \quad x \in \mathbb{R}, \quad t \geqslant 0,$$

  is solved by the leapfrog scheme

  $$u_{m}^{n+1}=\mu\left(u_{m+1}^{n}-u_{m-1}^{n}\right)+u_{m}^{n-1},$$

  where $n \geqslant 1$ and $\mu=\Delta t / \Delta x$ is the Courant number.

  (a) Determine the local error of the method.

  (b) Applying the Fourier technique, find the range of $\mu>0$ for which the method is stable.

  comment

• 3.II.38C

  Numerical Analysis

  Part II, 2008

  (a) A numerical method for solving the ordinary differential equation

  $$y^{\prime}(t)=f(t, y), \quad t \in[0, T], \quad y(0)=y_{0},$$

  generates for every $h>0$ a sequence $\left\{y_{n}\right\}$, where $y_{n}$ is an approximation to $y\left(t_{n}\right)$ and $t_{n}=n h$. Explain what is meant by the convergence of the method.

  (b) Prove from first principles that if the function $f$ is sufficiently smooth and satisfies the Lipschitz condition

  $$|f(t, x)-f(t, y)| \leqslant \lambda|x-y|, \quad x, y \in \mathbb{R}, \quad t \in[0, T],$$

  for some $\lambda>0$, then the trapezoidal rule

  $$y_{n+1}=y_{n}+\frac{1}{2} h\left[f\left(t_{n}, y_{n}\right)+f\left(t_{n+1}, y_{n+1}\right)\right]$$

  converges.

  comment

• 4.II.39C

  Numerical Analysis

  Part II, 2008

  Let $A \in \mathbb{R}^{n \times n}$ be a real matrix with $n$ linearly independent eigenvectors. When calculating eigenvalues of $A$, the sequence $\mathbf{x}^{(k)}, k=0,1,2, \ldots$, is generated by power method $\mathbf{x}^{(k+1)}=A \mathbf{x}^{(k)} /\left\|A \mathbf{x}^{(k)}\right\|$, where $\mathbf{x}^{(0)}$ is a real nonzero vector.

  (a) Describe the asymptotic properties of the sequence $\mathbf{x}^{(k)}$, both in the case where the eigenvalues $\lambda_{i}$ of $A$ satisfy $\left|\lambda_{i}\right|<\left|\lambda_{n}\right|, i=1, \ldots, n-1$, and in the case where $\left|\lambda_{i}\right|<\left|\lambda_{n-1}\right|=\left|\lambda_{n}\right|, i=1, \ldots, n-2$. In the latter case explain how the (possibly complexvalued) eigenvalues $\lambda_{n-1}, \lambda_{n}$ and their corresponding eigenvectors can be determined.

  (b) Let $n=3$, and suppose that, for a large $k$, we obtain the vectors

  $$\mathbf{y}_{k}=\mathbf{x}_{k}=\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right], \quad \mathbf{y}_{k+1}=A \mathbf{x}_{k}=\left[\begin{array}{l} 2 \\ 3 \\ 4 \end{array}\right], \quad \mathbf{y}_{k+2}=A^{2} \mathbf{x}_{k}=\left[\begin{array}{l} 2 \\ 4 \\ 6 \end{array}\right]$$

  Find two eigenvalues of $A$ and their corresponding eigenvectors.

  comment

• 4.I $3 \mathrm{G}$

  Geometry of Group Actions

  Part II, 2008

  Define the hyperbolic metric (in the sense of metric spaces) on the 3 -ball.

  Given a finite set in hyperbolic 3 -space, show there is at least one closed ball of minimal radius containing that set.

  comment

• 4.II.12G

  Geometry of Group Actions

  Part II, 2008

  What does it mean for a subgroup $G$ of the Möbius group to be discrete?

  Show that a discrete group necessarily acts properly discontinuously in hyperbolic 3-space.

  [You may assume that a discrete subgroup of a matrix group is a closed subset.]

  comment

• 1.I.4G

  Coding and Cryptography

  Part II, 2008

  Define the entropy $H(X)$ of a random variable $X$ that takes no more than $N$ different values. What are the maximum and the minimum values for the entropy for a fixed value of $N$ ? Explain when the maximum and minimum are attained. You should prove any inequalities that you use.

  comment

• 2.I.4G

  Coding and Cryptography

  Part II, 2008

  Describe briefly the Shannon-Fano and Huffman binary codes for a finite alphabet. Find examples of such codes for the alphabet $\mathcal{A}=\{a, b, c, d\}$ when the four letters are taken with probabilities $0.4,0.3,0.2$ and $0.1$ respectively.

  comment

• 3.I.1H

  Number Theory

  Part II, 2008

  Prove that, for all $x \geqslant 2$, we have

  $$\sum_{p \leqslant x} \frac{1}{p}>\log \log x-\frac{1}{2}$$

  [You may assume that, for $0<u<1$,

  $$-\log (1-u)-u<\frac{u^{2}}{2(1-u)} .$$

  comment

• 1.II.12G

  Coding and Cryptography

  Part II, 2008

  State Shannon's Noisy Coding Theorem for a binary symmetric channel.

  Define the mutual information of two discrete random variables $X$ and $Y$. Prove that the mutual information is symmetric and non-negative. Define also the information capacity of a channel.

  A channel transmits numbers chosen from the alphabet $\mathcal{A}=\{0,1,2\}$ and has transition matrix

  $$\left(\begin{array}{ccc} 1-2 \beta & \beta & \beta \\ \beta & 1-2 \beta & \beta \\ \beta & \beta & 1-2 \beta \end{array}\right)$$

  for a number $\beta$ with $0 \leqslant \beta \leqslant \frac{1}{3}$. Calculate the information capacity of the channel.

  comment

• 3.I.4G

  Coding and Cryptography

  Part II, 2008

  Define the Hamming code $h: \mathbb{F}_{2}^{4} \rightarrow \mathbb{F}_{2}^{7}$ and prove that the minimum distance between two distinct code words is 3. Explain how the Hamming code allows one error to be corrected.

  A new code $c: \mathbb{F}_{2}^{4} \rightarrow \mathbb{F}_{2}^{8}$ is obtained by using the Hamming code for the first 7 bits and taking the last bit as a check digit on the previous 7 . Find the minimum distance between two distinct code words for this code. How many errors can this code detect? How many errors can it correct?

  comment

• 2.II.12G

  Coding and Cryptography

  Part II, 2008

  Describe the Rabin cipher with modulus $N$, explaining how it can be deciphered by the intended recipient and why it is difficult for an interceptor to decipher it.

  The Bursars' Committee decides to communicate using Rabin ciphers to maintain confidentiality. The secretary of the committee encrypts a message, thought of as a positive integer $m$, using the Rabin cipher with modulus $N$ (with $0<m<N$ ) and publishes both the encrypted message and the modulus. A foolish bursar deciphers this message to read it but then encrypts it again using a Rabin cipher with a different modulus $N^{\prime}$ (with $\left.m<N^{\prime}\right)$ and publishes the newly encrypted message and $N^{\prime}$. The president of CUSU, who happens to be a talented mathematician, knows that this has happened. Explain how the president can work out what the original message was using the two different encrypted versions.

  Can the president of CUSU also decipher other messages sent out by the Bursars' Committee?

  comment

• 4.I.4G

  Coding and Cryptography

  Part II, 2008

  What is a binary cyclic code of length $N$ ? What is the generator polynomial for such a cyclic code? Prove that the generator polynomial is a factor of $X^{N}-1$ over the field $\mathbb{F}_{2}$.

  Find all the binary cyclic codes of length 5 .

  comment

• 1.I.5J

  Statistical Modelling

  Part II, 2008

  Consider the following Binomial generalized linear model for data $y_{1}, \ldots, y_{n}$, with logit link function. The data $y_{1}, \ldots, y_{n}$ are regarded as observed values of independent random variables $Y_{1}, \ldots, Y_{n}$, where

  $$Y_{i} \sim \operatorname{Bin}\left(1, \mu_{i}\right), \quad \log \frac{\mu_{i}}{1-\mu_{i}}=\beta^{\top} x_{i}, \quad i=1, \ldots, n,$$

  where $\beta$ is an unknown $p$-dimensional parameter, and where $x_{1}, \ldots, x_{n}$ are known $p$ dimensional explanatory variables. Write down the likelihood function for $y=\left(y_{1}, \ldots, y_{n}\right)$ under this model.

  Show that the maximum likelihood estimate $\hat{\beta}$ satisfies an equation of the form $X^{\top} y=X^{\top} \hat{\mu}$, where $X$ is the $p \times n$ matrix with rows $x_{1}^{\top}, \ldots, x_{n}^{\top}$, and where $\hat{\mu}=$ $\left(\hat{\mu}_{1}, \ldots, \hat{\mu}_{n}\right)$, with $\hat{\mu}_{i}$ a function of $x_{i}$ and $\hat{\beta}$, which you should specify.

  Define the deviance $D(y ; \hat{\mu})$ and find an explicit expression for $D(y ; \hat{\mu})$ in terms of $y$ and $\hat{\mu}$ in the case of the model above.

  comment

• 1.II.13J

  Statistical Modelling

  Part II, 2008

  Consider performing a two-way analysis of variance (ANOVA) on the following data: $>\mathrm{Y}[,, 1]$ $\mathrm{Y}[,, 2]$ $\mathrm{Y}[,, 3]$ $[, 1] \quad[, 2]$ $[, 1] \quad[, 2]$ $[, 1] \quad[, 2]$

  

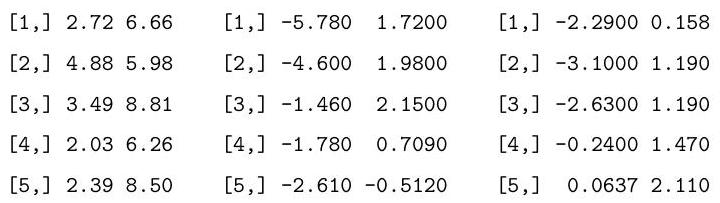
  Explain and interpret the R commands and (slightly abbreviated) output below. In particular, you should describe the model being fitted, and comment on the hypothesis tests which are performed under the summary and anova commands. $>\mathrm{K}<-\operatorname{dim}(\mathrm{Y})[1]$ $>I<-\operatorname{dim}(Y)[2]$ $>\mathrm{J}<-\operatorname{dim}(\mathrm{Y})[3]$ $>\mathrm{C}(\mathrm{I}, \mathrm{J}, \mathrm{K})$

  [1] $2 \quad 3 \quad 10$

  $>y<-$ as.vector $(Y)$

  $>\mathrm{a}<-\mathrm{gl}(\mathrm{I}, \mathrm{K}$, length $(\mathrm{y}))$

  $>\mathrm{b}<-\operatorname{gl}(\mathrm{J}, \mathrm{K} * \mathrm{I}$, length $(\mathrm{y}))$

  $>f i t 1<-\operatorname{lm}(\mathrm{y} \sim \mathrm{a}+\mathrm{b})$

  $>\operatorname{summary}(f i t 1)$

  Coefficients:

  Estimate Std. Error t value $\operatorname{Pr}(>|t|)$

  (Intercept) $3.7673 \quad 0.3032 \quad 12.43<2 \mathrm{e}-16 * * *$

  $\mathrm{a} 2 \quad 3.4542 \quad 0.3032 \quad 11.393 .27 \mathrm{e}-16 * * *$

  b2 $-6.3215<0.3713-17.03<2 \mathrm{e}-16 * * *$

  b3 $-5.8268<0.3713-15.69<2 \mathrm{e}-16 * * *$

  $>\operatorname{anova}(\mathrm{fit1})$

  

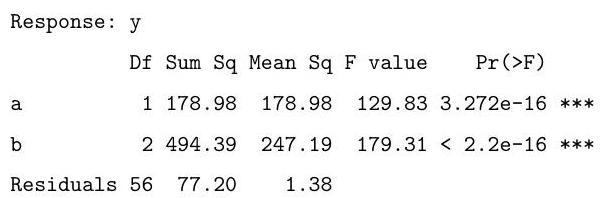
  The following $\mathrm{R}$ code fits a similar model. Briefly explain the difference between this model and the one above. Based on the output of the anova call below, say whether you prefer this model over the one above, and explain your preference.

  

  Finally, explain what is being calculated in the code below and give the value that would be obtained by the final line of code.

  

  comment

• $2 . \mathrm{I} . 5 \mathrm{~J} \quad$

  Statistical Modelling

  Part II, 2008

  Suppose that we want to estimate the angles $\alpha, \beta$ and $\gamma$ (in radians, say) of the triangle $A B C$, based on a single independent measurement of the angle at each corner. Suppose that the error in measuring each angle is normally distributed with mean zero and variance $\sigma^{2}$. Thus, we model our measurements $y_{A}, y_{B}, y_{C}$ as the observed values of random variables

  $$Y_{A}=\alpha+\varepsilon_{A}, \quad Y_{B}=\beta+\varepsilon_{B}, \quad Y_{C}=\gamma+\varepsilon_{C},$$

  where $\varepsilon_{A}, \varepsilon_{B}, \varepsilon_{C}$ are independent, each with distribution $N\left(0, \sigma^{2}\right)$. Find the maximum likelihood estimate of $\alpha$ based on these measurements.

  Can the assumption that $\varepsilon_{A}, \varepsilon_{B}, \varepsilon_{C} \sim N\left(0, \sigma^{2}\right)$ be criticized? Why or why not?

  comment

• 3.I.5J

  Statistical Modelling

  Part II, 2008

  Consider the linear model $Y=X \beta+\varepsilon$. Here, $Y$ is an $n$-dimensional vector of observations, $X$ is a known $n \times p$ matrix, $\beta$ is an unknown $p$-dimensional parameter, and $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$, with $\sigma^{2}$ unknown. Assume that $X$ has full rank and that $p \ll n$. Suppose that we are interested in checking the assumption $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$. Let $\hat{Y}=X \hat{\beta}$, where $\hat{\beta}$ is the maximum likelihood estimate of $\beta$. Write in terms of $X$ an expression for the projection matrix $P=\left(p_{i j}: 1 \leqslant i, j \leqslant n\right)$ which appears in the maximum likelihood equation $\hat{Y}=X \hat{\beta}=P Y$.

  Find the distribution of $\hat{\varepsilon}=Y-\hat{Y}$, and show that, in general, the components of $\hat{\varepsilon}$ are not independent.

  A standard procedure used to check our assumption on $\varepsilon$ is to check whether the studentized fitted residuals

  $$\hat{\eta}_{i}=\frac{\hat{\varepsilon}_{i}}{\tilde{\sigma} \sqrt{1-p_{i i}}}, \quad i=1, \ldots, n$$

  look like a random sample from an $N(0,1)$ distribution. Here,

  $$\tilde{\sigma}^{2}=\frac{1}{n-p}\|Y-X \hat{\beta}\|^{2} .$$

  Say, briefly, how you might do this in R.

  This procedure appears to ignore the dependence between the components of $\hat{\varepsilon}$ noted above. What feature of the given set-up makes this reasonable?

  comment

• 4.I $. 5 \mathrm{~J} \quad$

  Statistical Modelling

  Part II, 2008

  A long-term agricultural experiment had $n=90$ grassland plots, each $25 \mathrm{~m} \times 25 \mathrm{~m}$, differing in biomass, soil pH, and species richness (the count of species in the whole plot). While it was well-known that species richness declines with increasing biomass, it was not known how this relationship depends on soil pH. In the experiment, there were 30 plots of "low pH", 30 of "medium pH" and 30 of "high pH". Three lines of the data are reproduced here as an aid.

  Briefly explain the commands below. That is, explain the models being fitted.

  Let $H_{1}, H_{2}$ and $H_{3}$ denote the hypotheses represented by the three models and fits. Based on the output of the code below, what hypotheses are being tested, and which of the models seems to give the best fit to the data? Why?

  

  Finally, what is the value obtained by the following command?

  

  $$\begin{aligned} & >\operatorname{grass}[\mathrm{c}(1,31,61),] \\ & \text { pH Biomass Species } \\ & 1 \text { high } 0.4692972 \quad 30 \\ & 31 \text { mid } 0.1757627 \quad 29 \\ & 61 \text { low } 0.1008479 \quad 18 \\ & >\text { fit1 <- glm(Species Biomass, family = poisson) } \\ & >\text { fit2 <- glm(Species } ~ \mathrm{pH}+\text { Biomass, family }=\text { poisson) } \\ & >\text { fit3 <- glm(Species } \mathrm{pH} * \text { Biomass, family }=\text { poisson) } \end{aligned}$$

  comment

• 4.II.13J

  Statistical Modelling

  Part II, 2008

  Consider the following generalized linear model for responses $y_{1}, \ldots, y_{n}$ as a function of explanatory variables $x_{1}, \ldots, x_{n}$, where $x_{i}=\left(x_{i 1}, \ldots, x_{i p}\right)^{\top}$ for $i=1, \ldots, n$. The responses are modelled as observed values of independent random variables $Y_{1}, \ldots, Y_{n}$, with

  $$Y_{i} \sim \operatorname{ED}\left(\mu_{i}, \sigma_{i}^{2}\right), \quad g\left(\mu_{i}\right)=x_{i}^{\top} \beta, \quad \sigma_{i}^{2}=\sigma^{2} a_{i},$$

  Here, $g$ is a given link function, $\beta$ and $\sigma^{2}$ are unknown parameters, and the $a_{i}$ are treated as known.

  [Hint: recall that we write $Y \sim E D\left(\mu, \sigma^{2}\right)$ to mean that $Y$ has density function of the form

  $$f\left(y ; \mu, \sigma^{2}\right)=a\left(\sigma^{2}, y\right) \exp \left\{\frac{1}{\sigma^{2}}[\theta(\mu) y-K(\theta(\mu))]\right\}$$

  for given functions a and $\theta .]$

  [ You may use without proof the facts that, for such a random variable $Y$,

  $$\left.E(Y)=K^{\prime}(\theta(\mu)), \quad \operatorname{var}(Y)=\sigma^{2} K^{\prime \prime}(\theta(\mu)) \equiv \sigma^{2} V(\mu) .\right]$$

  Show that the score vector and Fisher information matrix have entries:

  $$U_{j}(\beta)=\sum_{i=1}^{n} \frac{\left(y_{i}-\mu_{i}\right) x_{i j}}{\sigma_{i}^{2} V\left(\mu_{i}\right) g^{\prime}\left(\mu_{i}\right)}, \quad j=1, \ldots, p$$

  and

  $$i_{j k}(\beta)=\sum_{i=1}^{n} \frac{x_{i j} x_{i k}}{\sigma_{i}^{2} V\left(\mu_{i}\right)\left(g^{\prime}\left(\mu_{i}\right)\right)^{2}}, \quad j, k=1, \ldots, p$$

  How do these expressions simplify when the canonical link is used?

  Explain briefly how these two expressions can be used to obtain the maximum likelihood estimate $\hat{\beta}$ for $\beta$.

  comment

• 3.II.11H

  Number Theory

  Part II, 2008

  State the reciprocity law for the Jacobi symbol.

  Let $a$ be an odd integer $>1$, which is not a square. Prove that there exists a positive integer $n$ such that $n \equiv 1 \bmod 4$ and

  $$\left(\frac{n}{a}\right)=-1$$

  Prove further that there exist infinitely many prime numbers $p$ such that

  $$\left(\frac{a}{p}\right)=-1$$

  comment

• 1.I.6B

  Mathematical Biology

  Part II, 2008

  A gene product with concentration $g$ is produced by a chemical $S$ of concentration $s$, is autocatalysed and degrades linearly according to the kinetic equation

  $$\frac{d g}{d t}=f(g, s)=s+k \frac{g^{2}}{1+g^{2}}-g$$

  where $k>0$ is a constant.

  First consider the case $s=0$. Show that if $k>2$ there are two positive steady states, and determine their stability. Sketch the reaction rate $f(g, 0)$.

  Now consider $s>0$. Show that there is a single steady state if $s$ exceeds a critical value. If the system starts in the steady state $g=0$ with $s=0$ and then $s$ is increased sufficiently before decreasing back to zero, show that a biochemical switch can be achieved to a state $g=g_{2}$, whose value you should determine.

  comment

• 2.I.6B

  Mathematical Biology

  Part II, 2008

  The population dynamics of a species is governed by the discrete model

  $$N_{t+1}=f\left(N_{t}\right)=N_{t} \exp \left[r\left(1-\frac{N_{t}}{K}\right)\right]$$

  where $r$ and $K$ are positive constants.

  Determine the steady states and their eigenvalues. Show that a period-doubling bifurcation occurs at $r=2$.

  Show graphically that the maximum possible population after $t=0$ is

  $$N_{\max }=f(K / r) .$$

  comment

• 2.II.13B

  Mathematical Biology

  Part II, 2008

  Consider the nonlinear equation describing the invasion of a population $u(x, t)$

  $$u_{t}=m u_{x x}+f(u)$$

  with $m>0, f(u)=-u(u-r)(u-1)$ and $0<r<1$ a constant.

  (a) Considering time-dependent spatially homogeneous solutions, show that there are two stable and one unstable uniform steady states.

  (b) In the case $r=\frac{1}{2}$, find the stationary 'front' which has

  $$u \rightarrow 1 \text { as } x \rightarrow-\infty \quad \text { and } \quad u \rightarrow 0 \text { as } x \rightarrow \infty$$

  [Hint: $f(u)=F^{\prime}(u)$ where $F(u)=-\frac{1}{4} u^{2}(1-u)^{2}+\frac{1}{6}\left(r-\frac{1}{2}\right) u^{2}(2 u-3)$.]

  (c) Now consider travelling-wave solutions to (1) of the form $u(x, t)=U(z)$ where $z=x-v t$. Show that $U$ satisfies an equation of the form

  $$m \ddot{U}+v \dot{U}=-V^{\prime}(U),$$

  where $\left({ }^{\cdot}\right) \equiv \frac{d}{d z}(\quad)$ and ()$^{\prime} \equiv \frac{d}{d U}(\quad)$.

  Sketch the form of $V(U)$ for $r=\frac{1}{2}, r>\frac{1}{2}$ and $r<\frac{1}{2}$. Using conditions (2), show that

  $$v \int_{-\infty}^{\infty} \dot{U}^{2} d z=F(1)-F(0) .$$

  Deduce how the sign of the travelling-wave velocity $v$ depends on $r$.

  comment

• 3.I.6B

  Mathematical Biology

  Part II, 2008

  An allosteric enzyme $E$ reacts with a substrate $S$ to produce a product $P$ according to the mechanism

  $$\begin{gathered} S+E \underset{k_{-1}}{\stackrel{k_{1}}{\rightleftharpoons}} C_{1} \stackrel{k_{2}}{\longrightarrow} E+P \\ S+C_{1} \underset{k_{-3}}{\stackrel{k_{3}}{\rightleftharpoons}} C_{2} \stackrel{k_{4}}{\rightarrow} C_{1}+P \end{gathered}$$

  where $C_{1}$ and $C_{2}$ are enzyme-substrate complexes. With lowercase letters denoting concentrations, write down a system of differential equations based on the Law of Mass Action which model this reaction mechanism.

  The initial conditions are $s=s_{0}, e=e_{0}, c_{1}=c_{2}=p=0 .$ Using $u=s / s_{0}$, $v_{i}=c_{i} / e_{0}, \tau=k_{1} e_{0} t$ and $\epsilon=e_{0} / s_{0}$, show that the nondimensional reaction mechanism reduces to

  $$\frac{d u}{d \tau}=f\left(u, v_{1}, v_{2}\right) \quad \text { and } \quad \epsilon \frac{d v_{i}}{d \tau}=g_{i}\left(u, v_{1}, v_{2}\right) \quad \text { for } \quad i=1,2$$

  finding expressions for $f, g_{1}$ and $g_{2}$.

  comment

• 3.II.13B

  Mathematical Biology

  Part II, 2008

  Consider the activator-inhibitor system in the fast-inhibitor limit

  $$\begin{gathered} u_{t}=D u_{x x}-u(u-r)(u-1)-\rho(v-u) \\ 0=v_{x x}-(v-u) \end{gathered}$$

  where $D$ is small, $0<r<1$ and $0<\rho<1$.

  Examine the linear stability of the state $u=v=0$ using perturbations of the form $\exp (i k x+\sigma t)$. Sketch the growth-rate $\sigma$ as a function of the wavenumber $k$. Find the growth-rate of the most unstable wave, and so determine the boundary in the $r$ - $\rho$ parameter plane which separates stable and unstable modes.

  Show that the system is unchanged under the transformation $u \rightarrow 1-u, v \rightarrow 1-v$ and $r \rightarrow 1-r$. Hence write down the equation for the boundary between stable and unstable modes of the state $u=v=1$.

  comment

• 4.I.6B

  Mathematical Biology

  Part II, 2008

  A semi-infinite elastic filament lies along the positive $x$-axis in a viscous fluid. When it is perturbed slightly to the shape $y=h(x, t)$, it evolves according to

  $$\zeta h_{t}=-A h_{x x x x}$$

  where $\zeta$ characterises the viscous drag and $A$ the bending stiffness. Motion is forced by boundary conditions

  $$h=h_{0} \cos (\omega t) \quad \text { and } \quad h_{x x}=0 \quad \text { at } \quad x=0, \quad \text { while } \quad h \rightarrow 0 \quad \text { as } \quad x \rightarrow \infty$$

  Use dimensional analysis to find the characteristic length $\ell(\omega)$ of the disturbance. Show that the steady oscillating solution takes the form

  $$h(x, t)=h_{0} \operatorname{Re}\left[e^{i \omega t} F(\eta)\right] \quad \text { with } \quad \eta=x / \ell,$$

  finding the ordinary differential equation for $F$.

  Find two solutions for $F$ which decay as $x \rightarrow \infty$. Without solving explicitly for the amplitudes, show that $h(x, t)$ is the superposition of two travelling waves which decay with increasing $x$, one with crests moving to the left and one to the right. Which dominates?

  comment

• 1.I.7A

  Dynamical Systems

  Part II, 2008

  Sketch the phase plane of the system

  $$\begin{aligned} &\dot{x}=y \\ &\dot{y}=-x+x^{2}-k y \end{aligned}$$

  (i) for $k=0$ and (ii) for $k=1 / 10$. Include in your sketches any trajectories that are the separatrices of a saddle point. In case (ii) shade the domain of stability of the origin.

  comment

• 3.II.14A

  Dynamical Systems

  Part II, 2008

  Define the Poincaré index of a simple closed curve, not necessarily a trajectory, and the Poincaré index of an isolated fixed point $\mathbf{x}_{0}$ for a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{2}$. State the Poincaré index of a periodic orbit.

  Consider the system

  $$\begin{aligned} &\dot{x}=y+a x-b x^{3} \\ &\dot{y}=x^{3}-x \end{aligned}$$

  where $a$ and $b$ are constants and $a \neq 0$.

  (a) Find and classify the fixed points, and state their Poincaré indices.

  (b) By considering a suitable function $H(x, y)$, show that any periodic orbit $\Gamma$ satisfies

  $$\oint_{\Gamma}\left(x-x^{3}\right)\left(a x-b x^{3}\right) d t=0$$

  where $x(t)$ is evaluated along the orbit.

  (c) Deduce that if $b / a<1$ then the second-order differential equation

  $$\ddot{x}-\left(a-3 b x^{2}\right) \dot{x}+x-x^{3}=0$$

  has no periodic solutions.

  comment

• 2.I.7A

  Dynamical Systems

  Part II, 2008

  Explain the difference between a stationary bifurcation and an oscillatory bifurcation for a fixed point $\mathbf{x}_{0}$ of a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x} ; \mu)$ in $\mathbb{R}^{n}$ with a real parameter $\mu$.

  The normal form of a Hopf bifurcation in polar coordinates is

  $$\begin{aligned} &\dot{r}=\mu r-a r^{3}+O\left(r^{5}\right) \\ &\dot{\theta}=\omega+c \mu-b r^{2}+O\left(r^{4}\right) \end{aligned}$$

  where $a, b, c$ and $\omega$ are constants, $a \neq 0$, and $\omega>0$. Sketch the phase plane near the bifurcation for each of the cases (i) $\mu<0<a$, (ii) $0<\mu, a$, (iii) $\mu, a<0$ and (iv) $a<0<\mu$.

  Let $R$ be the radius and $T$ the period of the limit cycle when one exists. Sketch how $R$ varies with $\mu$ for the case when the limit cycle is subcritical. Find the leading-order approximation to $d T / d \mu$ for $|\mu| \ll 1$.

  comment

• 4.II.14A

  Dynamical Systems

  Part II, 2008

  Explain the difference between a hyperbolic and a nonhyperbolic fixed point $\mathbf{x}_{0}$ for a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{n}$.

  Consider the system in $\mathbb{R}^{2}$, where $\mu$ is a real parameter,

  $$\begin{aligned} &\dot{x}=x\left(\mu-x+y^{2}\right) \\ &\dot{y}=y\left(1-x-y^{2}\right) \end{aligned}$$

  Show that the fixed point $(\mu, 0)$ has a bifurcation when $\mu=1$, while the fixed points $(0, \pm 1)$ have a bifurcation when $\mu=-1$.

  [The fixed point at $(0,-1)$ should not be considered further.]

  Analyse each of the bifurcations at $(\mu, 0)$ and $(0,1)$ in turn as follows. Make a change of variable of the form $\mathbf{X}=\mathbf{x}-\mathbf{x}_{0}(\mu), \nu=\mu-\mu_{0}$. Identify the (non-extended) stable and centre linear subspaces at the bifurcation in terms of $X$ and $Y$. By finding the leading-order approximation to the extended centre manifold, construct the evolution equation on the extended centre manifold, and determine the type of bifurcation. Sketch the local bifurcation diagram, showing which fixed points are stable.

  [Hint: the leading-order approximation to the extended centre manifold of the bifurcation at $(0,1)$ is $Y=a X$ for some coefficient a.]

  Show that there is another fixed point in $y>0$ for $\mu<1$, and that this fixed point connects the two bifurcations.

  comment

• 4.I.1H

  Number Theory

  Part II, 2008

  Let $p$ be an odd prime number. Assuming that the multiplicative group of $\mathbb{Z} / p \mathbb{Z}$ is cyclic, prove that the multiplicative group of units of $\mathbb{Z} / p^{n} \mathbb{Z}$ is cyclic for all $n \geqslant 1$.

  Find an integer $a$ such that its residue class in $\mathbb{Z} / 11^{n} \mathbb{Z}$ generates the multiplicative group of units for all $n \geqslant 1$.

  comment

• 3.I.7A

  Dynamical Systems

  Part II, 2008

  State the normal-form equations for (i) a saddle-node bifurcation, (ii) a transcritical bifurcation and (iii) a pitchfork bifurcation, for a one-dimensional map $x_{n+1}=F\left(x_{n} ; \mu\right)$.

  Consider a period-doubling bifurcation of the form

  $$x_{n+1}=-x_{n}+\alpha+\beta x_{n}+\gamma x_{n}^{2}+\delta x_{n}^{3}+O\left(x_{n}^{4}\right),$$

  where $x_{n}=O\left(\mu^{1 / 2}\right), \alpha, \beta=O(\mu)$, and $\gamma, \delta=O(1)$ as $\mu \rightarrow 0$. Show that

  $$X_{n+2}=X_{n}+\hat{\mu} X_{n}-A X_{n}^{3}+O\left(X_{n}^{4}\right),$$

  where $X_{n}=x_{n}-\frac{1}{2} \alpha$, and the parameters $\hat{\mu}$ and $A$ are to be identified in terms of $\alpha, \beta$, $\gamma$ and $\delta$. Deduce the condition for the bifurcation to be supercritical.

  comment

• 4.I.7A

  Dynamical Systems

  Part II, 2008

  Let $F: I \rightarrow I$ be a continuous one-dimensional map of an interval $I \subset \mathbb{R}$. State when $F$ is chaotic according to Glendinning's definition.

  Prove that if $F$ has a 3 -cycle then $F^{2}$ has a horseshoe.

  [You may assume the Intermediate Value Theorem.]

  comment

• 1.I.8C

  Further Complex Methods

  Part II, 2008

  The function $F$ is defined by

  $$F(z)=\int_{0}^{\infty} \frac{t^{z-1}}{(t+1)^{2}} d t$$

  For which values of $z$ does the integral converge?

  Show that, for these values,

  $$F(z)=\frac{\pi(1-z)}{\sin (\pi z)} .$$

  comment

• 2.I.8C

  Further Complex Methods

  Part II, 2008

  The Beta function is defined for $\operatorname{Re} z>0$ by

  $$\mathrm{B}(z, q)=\int_{0}^{1} t^{q-1}(1-t)^{z-1} d t \quad(\operatorname{Re} q>0)$$

  and by analytic continuation elsewhere in the complex $z$-plane.

  Show that

  $$\left(\frac{z+q}{z}\right) \mathrm{B}(z+1, q)=\mathrm{B}(z, q)$$

  and explain how this result can be used to obtain the analytic continuation of $\mathrm{B}(z, q)$. Hence show that $\mathrm{B}(z, q)$ is analytic except for simple poles and find the residues at the poles.

  comment

• 3.I.8C

  Further Complex Methods

  Part II, 2008

  What is the effect of the Möbius transformation $z \rightarrow \frac{z}{z-1}$ on the points $z=0$, $z=\infty$ and $z=1$ ?

  By considering

  $$(z-1)^{-a} P\left\{\begin{array}{cccc} 0 & \infty & 1 & \\ 0 & a & 0 & z(z-1)^{-1} \\ 1-c & c-b & b-a & \end{array}\right\}$$

  or otherwise, show that $(z-1)^{-a} F\left(a, c-b ; c ; z(z-1)^{-1}\right)$ is a branch of the $P$-function

  

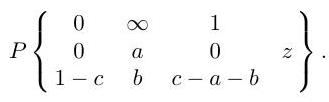
  Give a linearly independent branch.

  comment

• 1.II.14C

  Further Complex Methods

  Part II, 2008

  Show that under the change of variable $z=\sin ^{2} x$ the equation

  $$\frac{d^{2} w}{d x^{2}}+n^{2} w=0$$

  becomes

  $$\frac{d^{2} w}{d z^{2}}+\frac{2 z-1}{2 z(z-1)} \frac{d w}{d z}-\frac{n^{2}}{4(z-1) z} w=0$$

  Show that this is a Papperitz equation and that the corresponding $P$-function is

  $$P\left\{\begin{array}{rrrr} 0 & \infty & 1 & \\ 0 & \frac{1}{2} n & 0 & z \\ \frac{1}{2} & -\frac{1}{2} n & \frac{1}{2} & \end{array}\right\}$$

  Deduce that $F\left(\frac{1}{2} n,-\frac{1}{2} n ; \frac{1}{2} ; \sin ^{2} x\right)=\cos n x$.

  comment

• 4.I.8C

  Further Complex Methods

  Part II, 2008

  The Hilbert transform $\hat{f}$ of a function $f$ is defined by

  $$\hat{f}(t)=\frac{1}{\pi} \mathcal{P} \int_{-\infty}^{\infty} \frac{f(\tau)}{t-\tau} d \tau,$$

  where $\mathcal{P}$ denotes the Cauchy principal value.

  Show that the Hilbert transform of $\frac{\sin t}{t}$ is $\frac{1-\cos t}{t} .$

  comment

• 2.II.14C

  Further Complex Methods

  Part II, 2008

  (i) The function $f$ is defined by

  $$f(z)=\int_{C} t^{z-1} d t$$

  where $C$ is the circle $|t|=r$, described anti-clockwise starting on the positive real axis and where the value of $t^{z-1}$ at each point on $C$ is determined by analytic continuation along $C$ with $\arg t=0$ at the starting point. Verify by direct integration that $f$ is an entire function, the values of which depend on $r$.

  (ii) The function $J$ is defined by

  $$J(z)=\int_{\gamma} e^{t}\left(t^{2}-1\right)^{z} d t$$

  where $\gamma$ is a figure of eight, starting at $t=0$, looping anti-clockwise round $t=1$ and returning to $t=0$, then looping clockwise round $t=-1$ and returning again to $t=0$. The value of $\left(t^{2}-1\right)^{z}$ is determined by analytic continuation along $\gamma$ with $\arg \left(t^{2}-1\right)=-\pi$ at the start. Show that, for $\operatorname{Re} z>-1$,

  $$J(z)=-2 i \sin \pi z I(z),$$

  where

  $$I(z)=\int_{-1}^{1} e^{t}\left(t^{2}-1\right)^{z} d t$$

  Explain how this provides the analytic continuation of $I(z)$. Classify the singular points of the analytically continued function, commenting on the points $z=0,1, \ldots$.

  Explain briefly why the analytic continuation could not be obtained by this method if $\gamma$ were replaced by the circle $|t|=2$.

  comment

• 1.I.9A

  Classical Dynamics

  Part II, 2008

  The action for a system with generalized coordinates $q_{i}(t)$ for a time interval $\left[t_{1}, t_{2}\right]$ is given by

  $$S=\int_{t_{1}}^{t_{2}} L\left(q_{i}, \dot{q}_{i}, t\right) d t$$

  where $L$ is the Lagrangian. The end point values $q_{i}\left(t_{1}\right)$ and $q_{i}\left(t_{2}\right)$ are fixed.

  Derive Lagrange's equations from the principle of least action by considering the variation of $S$ for all possible paths.

  Define the momentum $p_{i}$ conjugate to $q_{i}$. Derive a condition for $p_{i}$ to be a constant of the motion.

  A symmetric top moves under the action of a potential $V(\theta)$. The Lagrangian is given by

  $$L=\frac{1}{2} I_{1}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-V$$

  where the generalized coordinates are the Euler angles $(\theta, \phi, \psi)$ and the principal moments of inertia are $I_{1}$ and $I_{3}$.

  Show that $\omega_{3}=\dot{\psi}+\dot{\phi} \cos \theta$ is a constant of the motion and give expressions for two others. Show further that it is possible for the top to move with both $\theta$ and $\dot{\phi}$ constant provided these satisfy the condition

  $$I_{1} \dot{\phi}^{2} \sin \theta \cos \theta-I_{3} \omega_{3} \dot{\phi} \sin \theta=\frac{d V}{d \theta}$$

  comment

• 2.II.15B

  Classical Dynamics

  Part II, 2008

  A particle of mass $m$, charge $e$ and position vector $\mathbf{r}=\left(x_{1}, x_{2}, x_{3}\right) \equiv \mathbf{q}$ moves in a magnetic field whose vector potential is A. Its Hamiltonian is given by

  $$H(\mathbf{p}, \mathbf{q})=\frac{1}{2 m}\left(\mathbf{p}-e \frac{\mathbf{A}}{c}\right)^{2}$$

  Write down Hamilton's equations and use them to derive the equations of motion for the charged particle.

  Define the Poisson bracket $[F, G]$ for general $F(\mathbf{p}, \mathbf{q})$ and $G(\mathbf{p}, \mathbf{q})$. Show that for motion governed by the above Hamiltonian

  $$\left[m \dot{x}_{i}, x_{j}\right]=-\delta_{i j}, \quad \text { and } \quad\left[m \dot{x}_{i}, m \dot{x}_{j}\right]=\frac{e}{c}\left(\frac{\partial A_{j}}{\partial x_{i}}-\frac{\partial A_{i}}{\partial x_{j}}\right)$$

  Consider the vector potential to be given by $\mathbf{A}=(0,0, F(r))$, where $r=\sqrt{x_{1}^{2}+x_{2}^{2}}$. Use Hamilton's equations to show that $p_{3}$ is constant and that circular motion at radius $r$ with angular frequency $\Omega$ is possible provided that

  $$\Omega^{2}=-\left(p_{3}-\frac{e F}{c}\right) \frac{e}{m^{2} c r} \frac{d F}{d r}$$

  comment

• 4.II.11H

  Number Theory

  Part II, 2008

  Let $N>1$ be an integer, which is not a square, and let $p_{k} / q_{k}(k=1,2, \ldots)$ be the convergents to $\sqrt{N}$. Prove that

  $$\left|p_{k}^{2}-q_{k}^{2} N\right|<2 \sqrt{N} \quad(k=1,2, \ldots)$$

  Explain briefly how this result can be used to generate a factor base $B$, and a set of $B$-numbers which may lead to a factorization of $N$.

  comment

• 2.I.9A

  Classical Dynamics

  Part II, 2008

  A system of $N$ particles $i=1,2,3, \ldots, N$, with mass $m_{i}$, moves around a circle of radius $a$. The angle between the radius to particle $i$ and a fixed reference radius is $\theta_{i}$. The interaction potential for the system is

  $$V=\frac{1}{2} k \sum_{j=1}^{N}\left(\theta_{j+1}-\theta_{j}\right)^{2}$$

  where $k$ is a constant and $\theta_{N+1}=\theta_{1}+2 \pi$.

  The Lagrangian for the system is

  $$L=\frac{1}{2} a^{2} \sum_{j=1}^{N} m_{j} \dot{\theta}_{j}^{2}-V$$

  Write down the equation of motion for particle $i$ and show that the system is in equilibrium when the particles are equally spaced around the circle.

  Show further that the system always has a normal mode of oscillation with zero frequency. What is the form of the motion associated with this?

  Find all the frequencies and modes of oscillation when $N=2, m_{1}=k m / a^{2}$ and $m_{2}=2 \mathrm{~km} / \mathrm{a}^{2}$, where $m$ is a constant.

  comment

• 3.I.9E

  Classical Dynamics

  Part II, 2008

  Writing $\mathbf{x}=\left(p_{1}, p_{2}, p_{3}, \ldots, p_{n}, q_{1}, q_{2}, q_{3}, \ldots, q_{n}\right)$, Hamilton's equations may be written in the form

  $$\dot{\mathbf{x}}=\mathbf{J} \frac{\partial H}{\partial \mathbf{x}} \text {, }$$

  where the $2 n \times 2 n$ matrix

  $$\mathbf{J}=\left(\begin{array}{rr} 0 & -I \\ I & 0 \end{array}\right)$$

  and $I$ and 0 denote the $n \times n$ unit and zero matrices respectively.

  Explain what is meant by the statement that the transformation $\mathbf{x} \rightarrow \mathbf{y}$,

  $$\left(p_{1}, p_{2}, p_{3}, \ldots, p_{n}, q_{1}, q_{2}, q_{3}, \ldots, q_{n}\right) \rightarrow\left(P_{1}, P_{2}, P_{3}, \ldots, P_{n}, Q_{1}, Q_{2}, Q_{3}, \ldots, Q_{n}\right)$$

  is canonical, and show that the condition for this is that

  $$\mathbf{J}=\mathcal{J} \mathbf{J} \mathcal{J}^{T}$$

  where $\mathcal{J}$ is the Jacobian matrix with elements

  $$\mathcal{J}_{i j}=\frac{\partial y_{i}}{\partial x_{j}}$$

  Use this condition to show that for a system with $n=1$ the transformation given by

  $$P=p+2 q, \quad Q=\frac{1}{2} q-\frac{1}{4} p$$

  is canonical.

  comment

• 4.II.15B

  Classical Dynamics

  Part II, 2008

  (a) A Hamiltonian system with $n$ degrees of freedom has Hamiltonian $H=H(\mathbf{p}, \mathbf{q})$, where the coordinates $\mathbf{q}=\left(q_{1}, q_{2}, q_{3}, \ldots, q_{n}\right)$ and the momenta $\mathbf{p}=\left(p_{1}, p_{2}, p_{3}, \ldots, p_{n}\right)$ respectively.

  Show from Hamilton's equations that when $H$ does not depend on time explicitly, for any function $F=F(\mathbf{p}, \mathbf{q})$,

  $$\frac{d F}{d t}=[F, H],$$

  where $[F, H]$ denotes the Poisson bracket.

  For a system of $N$ interacting vortices

  $$H(\mathbf{p}, \mathbf{q})=-\frac{\kappa}{4} \sum_{\substack{i=1 \\ N}}^{N} \sum_{\substack{j=1 \\ j \neq i}}^{N} \ln \left[\left(p_{i}-p_{j}\right)^{2}+\left(q_{i}-q_{j}\right)^{2}\right]$$

  where $\kappa$ is a constant. Show that the quantity defined by

  $$F=\sum_{j=1}^{N}\left(q_{j}^{2}+p_{j}^{2}\right)$$

  is a constant of the motion.

  (b) The action for a Hamiltonian system with one degree of freedom with $H=H(p, q)$ for which the motion is periodic is

  $$I=\frac{1}{2 \pi} \oint p(H, q) d q .$$

  Show without assuming any specific form for $H$ that the period of the motion $T$ is given by

  $$\frac{2 \pi}{T}=\frac{d H}{d I}$$

  Suppose now that the system has a parameter that is allowed to vary slowly with time. Explain briefly what is meant by the statement that the action is an adiabatic invariant. Suppose that when this parameter is fixed, $H=0$ when $I=0$. Deduce that, if $T$ decreases on an orbit with any $I$ when the parameter is slowly varied, then $H$ increases.

  comment

• 4.I.9B

  Classical Dynamics

  Part II, 2008

  (a) Show that the principal moments of inertia for an infinitesimally thin uniform rectangular sheet of mass $M$ with sides of length $a$ and $b$ (with $b<a$ ) about its centre of mass are $I_{1}=M b^{2} / 12, I_{2}=M a^{2} / 12$ and $I_{3}=M\left(a^{2}+b^{2}\right) / 12$.

  (b) Euler's equations governing the angular velocity $\left(\omega_{1}, \omega_{2}, \omega_{3}\right)$ of the sheet as viewed in the body frame are

  $$\begin{aligned} &I_{1} \frac{d \omega_{1}}{d t}=\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3} \\ &I_{2} \frac{d \omega_{2}}{d t}=\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1} \end{aligned}$$

  and

  $$I_{3} \frac{d \omega_{3}}{d t}=\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2} .$$

  A possible solution of these equations is such that the sheet rotates with $\omega_{1}=\omega_{3}=0$, and $\omega_{2}=\Omega=$ constant.

  By linearizing, find the equations governing small motions in the neighbourhood of this solution that have $\left(\omega_{1}, \omega_{3}\right) \neq 0$. Use these to show that there are solutions corresponding to instability such that $\omega_{1}$ and $\omega_{3}$ are both proportional to exp $(\beta \Omega t)$, with $\beta=\sqrt{\left(a^{2}-b^{2}\right) /\left(a^{2}+b^{2}\right)} .$

  comment

• 1.I.10E

  Cosmology

  Part II, 2008

  The number density of particles of mass $m$ at equilibrium in the early universe is given by the integral

  $$n=\frac{4 \pi g_{\mathrm{s}}}{h^{3}} \int_{0}^{\infty} \frac{p^{2} d p}{\exp [(E(p)-\mu) / k T] \mp 1}, \quad \begin{cases}- & \text { bosons } \\ + & \text { fermions }\end{cases}$$

  where $E(p)=c \sqrt{p^{2}+m^{2} c^{2}}, \mu$ is the chemical potential, and $g_{\mathrm{s}}$ is the spin degeneracy. Assuming that the particles remain in equilibrium when they become non-relativistic $\left(k T, \mu \ll m c^{2}\right)$, show that the number density can be expressed as

  $$n=g_{\mathrm{s}}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} e^{\left(\mu-m c^{2}\right) / k T} .$$

  [Hint: Recall that $\left.\int_{0}^{\infty} d x e^{-\sigma^{2} x^{2}}=\sqrt{\pi} /(2 \sigma), \quad(\sigma>0) .\right]$

  At around $t=100$ seconds, deuterium $D$ forms through the nuclear fusion of nonrelativistic protons $p$ and neutrons $n$ via the interaction $p+n \leftrightarrow D$. In equilibrium, what is the relationship between the chemical potentials of the three species? Show that the ratio of their number densities can be expressed as

  $$\frac{n_{D}}{n_{n} n_{p}} \approx\left(\frac{\pi m_{p} k T}{h^{2}}\right)^{-3 / 2} e^{B_{D} / k T}$$

  where the deuterium binding energy is $B_{D}=\left(m_{n}+m_{p}-m_{D}\right) c^{2}$ and you may take $g_{D}=4$. Now consider the fractional densities $X_{a}=n_{a} / n_{B}$, where $n_{B}$ is the baryon density of the universe, to re-express the ratio above in the form $X_{D} /\left(X_{n} X_{p}\right)$, which incorporates the baryon-to-photon ratio $\eta$ of the universe.

  [You may assume that the photon density is $n_{\gamma}=\left(16 \pi \zeta(3) /(h c)^{3}\right)(k T)^{3}$.]

  Why does deuterium form only at temperatures much lower than that given by $k T \approx B_{D}$ ?

  comment

• 2.I.10E

  Cosmology

  Part II, 2008

  A spherically-symmetric star obeys the pressure-support equation

  $$\frac{d P}{d r}=-\frac{G m \rho}{r^{2}}$$

  where $P(r)$ is the pressure at a distance $r$ from the centre, $\rho(r)$ is the density, and $m(r)$ is the mass within a sphere of radius $r$. Show that this implies

  $$\frac{d}{d r}\left(\frac{r^{2}}{\rho} \frac{d P}{d r}\right)=-4 \pi G r^{2} \rho$$

  Propose and justify appropriate boundary conditions for the pressure $P(r)$ at the centre of the star $(r=0)$ and at its outer edge $r=R$.

  Show that the function

  $$F(r)=P(r)+\frac{G m^{2}}{8 \pi r^{4}}$$

  is a decreasing function of $r$. Deduce that the central pressure $P_{\mathrm{c}} \equiv P(0)$ satisfies

  $$P_{\mathrm{c}}>\frac{G M^{2}}{8 \pi R^{4}},$$

  where $M \equiv m(R)$ is the mass of the star.

  comment

• 1.II.15E

  Cosmology

  Part II, 2008

  (i) A homogeneous and isotropic universe has mass density $\rho(t)$ and scale factor $a(t)$. Show how the conservation of total energy (kinetic plus gravitational potential) when applied to a test particle on the edge of a spherical region in this universe can be used to obtain the Friedmann equation

  $$H^{2} \equiv\left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi G}{3} \rho-\frac{k c^{2}}{a^{2}},$$

  where $k$ is a constant. State clearly any assumptions you have made.

  (ii) Assume that the universe is flat $(k=0)$ and filled with two major components: pressure-free matter $\left(P_{\mathrm{M}}=0\right)$ and dark energy with equation of state $P_{\Lambda}=-\rho_{\Lambda} c^{2}$ where their mass densities today $\left(t=t_{0}\right)$ are given respectively by $\rho_{\mathrm{M} 0}$ and $\rho_{\Lambda 0}$. Assuming that each component independently satisfies the fluid conservation equation, $\dot{\rho}=-3 H\left(\rho+P / c^{2}\right)$, show that the total mass density can be expressed as

  $$\rho(t)=\frac{\rho_{\mathrm{M} 0}}{a^{3}}+\rho_{\Lambda 0}$$

  where we have set $a\left(t_{0}\right)=1$.

  Hence, solve the Friedmann equation and show that the scale factor can be expressed in the form

  $$a(t)=\alpha(\sinh \beta t)^{2 / 3},$$

  where $\alpha$ and $\beta$ are constants which you should specify in terms of $\rho_{\mathrm{M} 0}, \rho_{\Lambda 0}$ and $t_{0}$.

  [Hint: try the substitution $b=a^{3 / 2}$.]

  Show that the scale factor $a(t)$ has the expected behaviour for a matter-dominated universe at early times $(t \rightarrow 0)$ and that the universe accelerates at late times $(t \rightarrow \infty)$.

  comment

• $3 . \mathrm{I} . 10 \mathrm{E} \quad$

  Cosmology

  Part II, 2008

  The energy density $\epsilon$ and pressure $P$ of photons in the early universe is given by

  $$\epsilon=\frac{4 \sigma}{c} T^{4}, \quad P=\frac{1}{3} \epsilon,$$

  where $\sigma$ is the Stefan-Boltzmann constant. By using the first law of thermodynamics $d E=T d S-P d V+\mu d N$, deduce that the entropy differential $d S$ can be expressed in the form

  $$d S=\frac{16 \sigma}{3 c} d\left(T^{3} V\right)$$

  With the third law, show that the entropy density is given by $s=(16 \sigma / 3 c) T^{3}$.

  While particle interaction rates $\Gamma$ remain much greater than the Hubble parameter $H$, justify why entropy will be conserved during the expansion of the universe. Hence, in the early universe (radiation domination) show that the temperature $T \propto a^{-1}$ where $a(t)$ is the scale factor of the universe, and show that the Hubble parameter $H \propto T^{2}$.

  comment

• 4.I.10E

  Cosmology

  Part II, 2008

  The Friedmann and Raychaudhuri equations are respectively

  $$\left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi G}{3} \rho-\frac{k c^{2}}{a^{2}} \quad \text { and } \quad \frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+\frac{3 P}{c^{2}}\right) \text {, }$$

  where $\rho$ is the mass density, $P$ is the pressure, $k$ is the curvature and $\dot{a} \equiv d a / d t$ with $t$ the cosmic time. Using conformal time $\tau$ (defined by $d \tau=d t / a$ ) and the equation of state $P=w \rho c^{2}$, show that these can be rewritten as

  $$\frac{k c^{2}}{\mathcal{H}^{2}}=\Omega-1 \quad \text { and } \quad 2 \frac{d \mathcal{H}}{d \tau}=-(3 w+1)\left(\mathcal{H}^{2}+k c^{2}\right)$$

  where $\mathcal{H}=a^{-1} d a / d \tau$ and the relative density is $\Omega \equiv \rho / \rho_{\text {crit }}=8 \pi G \rho a^{2} /\left(3 \mathcal{H}^{2}\right)$.

  Use these relations to derive the following evolution equation for $\Omega$

  $$\frac{d \Omega}{d \tau}=(3 w+1) \mathcal{H} \Omega(\Omega-1)$$

  For both $w=0$ and $w=-1$, plot the qualitative evolution of $\Omega$ as a function of $\tau$ in an expanding universe $\mathcal{H}>0$ (i.e. include curves initially with $\Omega>1$ and $\Omega<1$ ).

  Hence, or otherwise, briefly describe the flatness problem of the standard cosmology and how it can be solved by inflation.

  comment

• $3 . \mathrm{II} . 15 \mathrm{E} \quad$

  Cosmology

  Part II, 2008

  Small density perturbations $\delta_{\mathbf{k}}(t)$ in pressureless matter inside the cosmological horizon obey the following Fourier evolution equation

  $$\ddot{\delta}_{\mathbf{k}}+2 \frac{\dot{a}}{a} \dot{\delta}_{\mathbf{k}}-4 \pi G \bar{\rho}_{\mathrm{c}} \delta_{\mathbf{k}}=0$$

  where $\bar{\rho}_{\mathrm{c}}$ is the average background density of the pressureless gravitating matter and $\mathbf{k}$ is the comoving wavevector.

  (i) Seek power law solutions $\delta_{\mathbf{k}} \propto t^{\beta}(\beta$ constant) during the matter-dominated epoch $\left(t_{\mathrm{eq}}<t<t_{0}\right)$ to find the approximate solution

  $$\delta_{\mathbf{k}}(t)=A(\mathbf{k})\left(\frac{t}{t_{\mathrm{eq}}}\right)^{2 / 3}+B(\mathbf{k})\left(\frac{t}{t_{\mathrm{eq}}}\right)^{-1}, \quad t \gg t_{\mathrm{eq}}$$

  where $A, B$ are functions of $\mathbf{k}$ only and $t_{\mathrm{eq}}$ is the time of equal matter-radiation.

  By considering the behaviour of the scalefactor $a$ and the relative density $\bar{\rho}_{\mathrm{c}} / \bar{\rho}_{\text {total }}$, show that early in the radiation era $\left(t \ll t_{\mathrm{eq}}\right)$ there is effectively no significant perturbation growth in $\delta_{\mathbf{k}}$ on sub-horizon scales.

  (ii) For a given wavenumber $k=|\mathbf{k}|$, show that the time $t_{\mathrm{H}}$ at which this mode crosses inside the horizon, i.e., $c t_{\mathrm{H}} \approx 2 \pi a\left(t_{\mathrm{H}}\right) / k$, is given by

  $$\frac{t_{\mathrm{H}}}{t_{0}} \approx \begin{cases}\left(\frac{k_{0}}{k}\right)^{3}, & t_{\mathrm{H}} \gg t_{\mathrm{eq}} \\ \left(1+z_{\mathrm{eq}}\right)^{-1 / 2}\left(\frac{k_{0}}{k}\right)^{2}, & t_{\mathrm{H}} \ll t_{\mathrm{eq}}\end{cases}$$

  where $k_{0} \equiv 2 \pi /\left(c t_{0}\right)$, and the equal matter-radiation redshift is given by $1+z_{\mathrm{eq}}=$ $\left(t_{0} / t_{\mathrm{eq}}\right)^{2 / 3}$.

  Assume that primordial perturbations from inflation are scale-invariant with a constant amplitude as they cross the Hubble radius given by $\left\langle\left|\delta_{\mathbf{k}}\left(t_{\mathrm{H}}\right)\right|^{2}\right\rangle \approx V^{-1} A / k^{3}$, where $A$ is a constant and $V$ is a large volume. Use the results of (i) to project these perturbations forward to $t_{0}$, and show that the power spectrum for perturbations today will be given approximately by

  $$P(k) \equiv V\left\langle\left|\delta_{\mathbf{k}}\left(t_{0}\right)\right|^{2}\right\rangle \approx \frac{A}{k_{0}^{4}} \times \begin{cases}k, & k<k_{\mathrm{eq}} \\ k_{\mathrm{eq}}\left(\frac{k_{\mathrm{eq}}}{k}\right)^{3}, & k>k_{\mathrm{eq}}\end{cases}$$

  comment

• 1.I.2F

  Topics in Analysis

  Part II, 2008

  Let $P_{0}, P_{1}, P_{2}, \ldots$ be non-zero orthogonal polynomials on an interval $[a, b]$ such that the degree of $P_{j}$ is equal to $j$ for every $j=0,1,2, \ldots$, where the orthogonality is with respect to the inner product $<f, g>=\int_{a}^{b} f g$. If $f$ is any continuous function on $[a, b]$ orthogonal to $P_{0}, P_{1}, \ldots, P_{n-1}$ and not identically zero, prove that $f$ must have at least $n$ distinct zeros in $(a, b)$.

  comment

• 1.II.16G

  Logic and Set Theory

  Part II, 2008

  What is a well-ordered set? Show that given any two well-ordered sets there is a unique order isomorphism between one and an initial segment of the other.

  Show that for any ordinal $\alpha$ and for any non-zero ordinal $\beta$ there are unique ordinals $\gamma$ and $\delta$ with $\alpha=\beta \cdot \gamma+\delta$ and $\delta<\beta$.

  Show that a non-zero ordinal $\lambda$ is a limit ordinal if and only if $\lambda=\omega \cdot \gamma$ for some non-zero ordinal $\gamma$.

  [You may assume standard properties of ordinal addition, multiplication and subtraction.]

  comment

• 2.II.16G

  Logic and Set Theory

  Part II, 2008

  (i) State the Completeness Theorem and the Compactness Theorem for the predicate calculus.

  (ii) Show that if a theory has arbitrarily large finite models then it has an infinite model. Deduce that there is no first order theory whose models are just the finite fields of characteristic 2 . Show that the theory of infinite fields of characteristic 2 does not have a finite axiomatisation.

  (iii) Let $\mathcal{T}$ be the collection of closed terms in some first order language $\mathcal{L}$. Suppose that $\exists x . \phi(x)$ is a provable sentence of $\mathcal{L}$ with $\phi$ quantifier-free. Show that the set of sentences $\{\neg \phi(t): t \in \mathcal{T}\}$ is inconsistent.

  [Hint: consider the minimal substructure of a model.]

  Deduce that there are $t_{1}, t_{2}, \ldots, t_{n}$ in $\mathcal{T}$ such that $\phi\left(t_{1}\right) \vee \phi\left(t_{2}\right) \vee \cdots \vee \phi\left(t_{n}\right)$ is provable.

  comment

• 3.II.16G

  Logic and Set Theory

  Part II, 2008

  What is a transitive set? Show that if $x$ is transitive then so are the union $\bigcup x$ and the power set $P x$ of $x$. If $\bigcup x$ is transitive, is $x$ transitive? If $P x$ is transitive, is $x$ transitive? Justify your answers.

  What is the transitive closure of a set? Show that any set $x$ has a transitive closure $T C(x)$.

  Suppose that $x$ has rank $\alpha$. What is the rank of $P x$ ? What is the rank of $T C(x)$ ?

  [You may use standard properties of rank.]

  comment

• 4.II.16G

  Logic and Set Theory

  Part II, 2008

  Prove Hartog's Lemma that for any set $x$ there is an ordinal $\alpha$ which cannot be mapped injectively into $x$.

  Now assume the Axiom of Choice. Prove Zorn's Lemma and the Well-ordering Principle.

  [If you appeal to a fixed point theorem then you should state it clearly.]

  comment

• 1.II .17F

  Graph Theory

  Part II, 2008

  State a result of Euler concerning the number of vertices, edges and faces of a connected plane graph. Deduce that if $G$ is a planar graph then $\delta(G) \leqslant 5$. Show that if $G$ is a planar graph then $\chi(G) \leqslant 5$.

  Are the following statements true or false? Justify your answers.

  [You may quote standard facts about planar and non-planar graphs, provided that they are clearly stated.]

  (i) If $G$ is a graph with $\chi(G) \leqslant 4$ then $G$ is planar.

  (ii) If $G$ is a connected graph with average degree at most $2.01$ then $G$ is planar.

  (iii) If $G$ is a connected graph with average degree at most 2 then $G$ is planar.

  comment

• 2.II.17F

  Graph Theory

  Part II, 2008

  Prove that every graph $G$ on $n \geqslant 3$ vertices with minimum degree $\delta(G) \geqslant \frac{n}{2}$ is Hamiltonian. For each $n \geqslant 3$, give an example to show that this result does not remain true if we weaken the condition to $\delta(G) \geqslant \frac{n}{2}-1$ (for $n$ even) or $\delta(G) \geqslant \frac{n-1}{2}$ (for $n$ odd).

  For any graph $G$, let $G_{k}$ denote the graph formed by adding $k$ new vertices to $G$, all joined to each other and to all vertices of $G$. By considering $G_{1}$, show that if $G$ is a graph on $n \geqslant 3$ vertices with $\delta(G) \geqslant \frac{n-1}{2}$ then $G$ has a Hamilton path (a path passing through all the vertices of $G$ ).

  For each positive integer $k$, exhibit a connected graph $G$ such that $G_{k}$ is not Hamiltonian. Is this still possible if we replace 'connected' with '2-connected'?

  comment

• 3.II $. 17 \mathrm{~F} \quad$

  Graph Theory

  Part II, 2008

  Define the chromatic polynomial $p_{G}(t)$ of a graph $G$. Show that if $G$ has $n$ vertices and $m$ edges then

  $$p_{G}(t)=a_{n} t^{n}-a_{n-1} t^{n-1}+a_{n-2} t^{n-2}-\ldots+(-1)^{n} a_{0}$$

  where $a_{n}=1$ and $a_{n-1}=m$ and $a_{i} \geqslant 0$ for all $0 \leqslant i \leqslant n$. [You may assume the deletion-contraction relation, provided it is clearly stated.]

  Show that if $G$ is a tree on $n$ vertices then $p_{G}(t)=t(t-1)^{n-1}$. Does the converse hold?

  [Hint: if $G$ is disconnected, how is the chromatic polynomial of $G$ related to the chromatic polynomials of its components?]

  Show that if $G$ is a graph on $n$ vertices with the same chromatic polynomial as $T_{r}(n)$ (the Turán graph on $n$ vertices with $r$ vertex classes) then $G$ must be isomorphic to $T_{r}(n)$.

  comment

• 4.II.17F

  Graph Theory

  Part II, 2008

  For $s \geqslant 2$, let $R(s)$ be the least integer $n$ such that for every 2 -colouring of the edges of $K_{n}$ there is a monochromatic $K_{s}$. Prove that $R(s)$ exists.

  For any $k \geqslant 1$ and $s_{1}, \ldots, s_{k} \geqslant 2$, define the Ramsey number $R_{k}\left(s_{1}, \ldots, s_{k}\right)$, and prove that it exists.

  Show that, whenever the positive integers are partitioned into finitely many classes, some class contains $x, y, z$ with $x+y=z$.

  [Hint: given a finite colouring of the positive integers, induce a colouring of the pairs of positive integers by giving the pair $i j(i<j)$ the colour of $j-i$.]

  comment

• 1.II.18H

  Galois Theory

  Part II, 2008

  Find the Galois group of the polynomial $f(x)=x^{4}+x^{3}+1$ over (i) the finite field $\mathbf{F}_{2}$, (ii) the finite field $\mathbf{F}_{3}$, (iii) the finite field $\mathbf{F}_{4}$, (iv) the field $\mathbf{Q}$ of rational numbers.

  [Results from the course which you use should be stated precisely.]

  comment

• 2.II.18H

  Galois Theory

  Part II, 2008

  (i) Let $K$ be a field, $\theta \in K$, and $n>0$ not divisible by the characteristic. Suppose that $K$ contains a primitive $n$th root of unity. Show that the splitting field of $x^{n}-\theta$ has cyclic Galois group.

  (ii) Let $L / K$ be a Galois extension of fields and $\zeta_{n}$ denote a primitive $n$th root of unity in some extension of $L$, where $n$ is not divisible by the characteristic. Show that $\operatorname{Aut}\left(L\left(\zeta_{n}\right) / K\left(\zeta_{n}\right)\right)$ is a subgroup of $\operatorname{Aut}(L / K)$.

  (iii) Determine the minimal polynomial of a primitive 6 th root of unity $\zeta_{6}$ over $\mathbf{Q}$.

  Compute the Galois group of $x^{6}+3 \in \mathbf{Q}[x]$.

  comment

• 2.II.11F

  Topics in Analysis

  Part II, 2008

  Let $L: C([0,1]) \rightarrow C([0,1])$ be an operator satisfying the conditions

  (i) $L f \geqslant 0$ for any $f \in C([0,1])$ with $f \geqslant 0$,

  (ii) $L(a f+b g)=a L f+b L g$ for any $f, g \in C([0,1])$ and $a, b \in \mathbf{R}$ and

  (iii) $Z_{f} \subseteq Z_{L f}$ for any $f \in C([0,1])$, where $Z_{f}$ denotes the set of zeros of $f$.

  Prove that there exists a function $h \in C([0,1])$ with $h \geqslant 0$ such that $L f=h f$ for every $f \in C([0,1])$.

  comment

• 3.II.18H

  Galois Theory

  Part II, 2008

  Let $L / K$ be a field extension.

  (a) State what it means for $\alpha \in L$ to be algebraic over $K$, and define its degree $\operatorname{deg}_{K}(\alpha)$. Show that if $\operatorname{deg}_{K}(\alpha)$ is odd, then $K(\alpha)=K\left(\alpha^{2}\right)$.

  [You may assume any standard results.]

  Show directly from the definitions that if $\alpha, \beta \in L$ are algebraic over $K$, then so too is $\alpha+\beta$.

  (b) State what it means for $\alpha \in L$ to be separable over $K$, and for the extension $L / K$ to be separable.

  Give an example of an inseparable extension $L / K$.

  Show that an extension $L / K$ is separable if $L$ is a finite field.

  comment

• 4.II.18H

  Galois Theory

  Part II, 2008

  Let $L=\mathbf{C}(z)$ be the function field in one variable, $n>0$ an integer, and $\zeta_{n}=e^{2 \pi i / n}$.

  Define $\sigma, \tau: L \rightarrow L$ by the formulae

  $$(\sigma f)(z)=f\left(\zeta_{n} z\right), \quad(\tau f)(z)=f(1 / z),$$

  and let $G=\langle\sigma, \tau\rangle$ be the group generated by $\sigma$ and $\tau$.

  (i) Find $w \in \mathbf{C}(z)$ such that $L^{G}=\mathbf{C}(w)$.

  [You must justify your answer, stating clearly any theorems you use.]

  (ii) Suppose $n$ is an odd prime. Determine the subgroups of $G$ and the corresponding intermediate subfields $M$, with $\mathbf{C}(w) \subseteq M \subseteq L$.

  State which intermediate subfields $M$ are Galois extensions of $\mathbf{C}(w)$, and for these extensions determine the Galois group.

  comment

• 1.II.19G

  Representation Theory

  Part II, 2008

  For a complex representation $V$ of a finite group $G$, define the action of $G$ on the dual representation $V^{*}$. If $\alpha$ denotes the character of $V$, compute the character $\beta$ of $V^{*}$.

  [Your formula should express $\beta(g)$ just in terms of the character $\alpha$.]

  Using your formula, how can you tell from the character whether a given representation is self-dual, that is, isomorphic to the dual representation?

  Let $V$ be an irreducible representation of $G$. Show that the trivial representation occurs as a summand of $V \otimes V$ with multiplicity either 0 or 1 . Show that it occurs once if and only if $V$ is self-dual.

  For a self-dual irreducible representation $V$, show that $V$ either has a nondegenerate $G$-invariant symmetric bilinear form or a nondegenerate $G$-invariant alternating bilinear form, but not both.

  If $V$ is an irreducible self-dual representation of odd dimension $n$, show that the corresponding homomorphism $G \rightarrow G L(n, \mathbf{C})$ is conjugate to a homomorphism into the orthogonal group $O(n, \mathbf{C})$. Here $O(n, \mathbf{C})$ means the subgroup of $G L(n, \mathbf{C})$ that preserves a nondegenerate symmetric bilinear form on $\mathbf{C}^{n}$.

  comment

• 2.II.19G

  Representation Theory

  Part II, 2008

  A finite group $G$ of order 360 has conjugacy classes $C_{1}=\{1\}, C_{2}, \ldots, C_{7}$ of sizes $1,45,40,40,90,72,72$. The values of four of its irreducible characters are given in the following table.

  $$\begin{array}{ccccccc} C_{1} & C_{2} & C_{3} & C_{4} & C_{5} & C_{6} & C_{7} \\ 5 & 1 & 2 & -1 & -1 & 0 & 0 \\ 8 & 0 & -1 & -1 & 0 & (1-\sqrt{5}) / 2 & (1+\sqrt{5}) / 2 \\ 8 & 0 & -1 & -1 & 0 & (1+\sqrt{5}) / 2 & (1-\sqrt{5}) / 2 \\ 10 & -2 & 1 & 1 & 0 & 0 & 0 \end{array}$$

  Complete the character table.

  [Hint: it will not suffice just to use orthogonality of characters.]

  Deduce that the group $G$ is simple.

  comment

• 3.II.19G

  Representation Theory

  Part II, 2008

  Let $V_{2}$ denote the irreducible representation $\operatorname{Sym}^{2}\left(\mathbb{C}^{2}\right)$ of $S U(2)$; thus $V_{2}$ has dimension 3. Compute the character of the representation $\operatorname{Sym}^{n}\left(V_{2}\right)$ of $S U(2)$ for any $n \geqslant 0$. Compute the dimension of the invariants $\operatorname{Sym}^{n}\left(V_{2}\right)^{S U(2)}$, meaning the subspace of $\operatorname{Sym}^{n}\left(V_{2}\right)$ where $S U(2)$ acts trivially.

  Hence, or otherwise, show that the ring of complex polynomials in three variables $x, y, z$ which are invariant under the action of $S O(3)$ is a polynomial ring. Find a generator for this polynomial ring.

  comment

• 4.II.19G

  Representation Theory

  Part II, 2008

  (a) Let $A$ be a normal subgroup of a finite group $G$, and let $V$ be an irreducible representation of $G$. Show that either $V$ restricted to $A$ is isotypic (a sum of copies of one irreducible representation of $A)$, or else $V$ is induced from an irreducible representation of some proper subgroup of $G$.

  (b) Using (a), show that every (complex) irreducible representation of a $p$-group is induced from a 1-dimensional representation of some subgroup.

  [You may assume that a nonabelian $p$-group $G$ has an abelian normal subgroup $A$ which is not contained in the centre of $G$.]

  comment

• 1.II.20G

  Number Fields

  Part II, 2008

  (a) Define the ideal class group of an algebraic number field $K$. State a result involving the discriminant of $K$ that implies that the ideal class group is finite.

  (b) Put $K=\mathbb{Q}(\omega)$, where $\omega=\frac{1}{2}(1+\sqrt{-23})$, and let $\mathcal{O}_{K}$ be the ring of integers of $K$. Show that $\mathcal{O}_{K}=\mathbb{Z}+\mathbb{Z} \omega$. Factorise the ideals [2] and [3] in $\mathcal{O}_{K}$ into prime ideals. Verify that the equation of ideals

  $$[2, \omega][3, \omega]=[\omega]$$

  holds. Hence prove that $K$ has class number 3 .

  comment

• 2.II.20G

  Number Fields

  Part II, 2008

  (a) Factorise the ideals [2], [3] and [5] in the ring of integers $\mathcal{O}_{K}$ of the field $K=\mathbb{Q}(\sqrt{30})$. Using Minkowski's bound

  $$\frac{n !}{n^{n}}\left(\frac{4}{\pi}\right)^{s} \sqrt{\left|d_{K}\right|},$$

  determine the ideal class group of $K$.

  [Hint: it might be helpful to notice that $\frac{3}{2}=N_{K / \mathbb{Q}}(\alpha)$ for some $\left.\alpha \in K .\right]$

  (b) Find the fundamental unit of $K$ and determine all solutions of the equations $x^{2}-30 y^{2}=\pm 5$ in integers $x, y \in \mathbb{Z}$. Prove that there are in fact no solutions of $x^{2}-30 y^{2}=5$ in integers $x, y \in \mathbb{Z}$.

  comment

• 4.II.20G

  Number Fields

  Part II, 2008

  (a) Explain what is meant by an integral basis of an algebraic number field. Specify such a basis for the quadratic field $k=\mathbb{Q}(\sqrt{2})$.

  (b) Let $K=\mathbb{Q}(\alpha)$ with $\alpha=\sqrt[4]{2}$, a fourth root of 2 . Write an element $\theta$ of $K$ as

  $$\theta=a+b \alpha+c \alpha^{2}+d \alpha^{3}$$

  with $a, b, c, d \in \mathbb{Q}$. By computing the relative traces $T_{K / k}(\theta)$ and $T_{K / k}(\alpha \theta)$, show that if $\theta$ is an algebraic integer of $K$, then $2 a, 2 b, 2 c$ and $4 d$ are rational integers. By further computing the relative norm $N_{K / k}(\theta)$, show that

  $$a^{2}+2 c^{2}-4 b d \text { and } 2 a c-b^{2}-2 d^{2}$$

  are rational integers. Deduce that $1, \alpha, \alpha^{2}, \alpha^{3}$ is an integral basis of $K$.

  comment

• 1.II.21F

  Algebraic Topology

  Part II, 2008

  (i) State the van Kampen theorem.

  (ii) Calculate the fundamental group of the wedge $S^{2} \vee S^{1}$.

  (iii) Let $X=\mathbb{R}^{3} \backslash A$ where $A$ is a circle. Calculate the fundamental group of $X$.

  comment

• $2 . \mathrm{I} . 2 \mathrm{~F} \quad$

  Topics in Analysis

  Part II, 2008

  (a) State Brouwer's fixed point theorem in the plane and prove that the statement is equivalent to non-existence of a continuous retraction of the closed disk $D$ to its boundary $\partial D$.

  (b) Use Brouwer's fixed point theorem to prove that there is a complex number $z$ in the closed unit disc such that $z^{6}-z^{5}+2 z^{2}+6 z+1=0$.

  comment

• 2.II.21F

  Algebraic Topology

  Part II, 2008

  Prove the Borsuk-Ulam theorem in dimension 2: there is no map $f: S^{2} \rightarrow S^{1}$ such that $f(-x)=-f(x)$ for every $x \in S^{2}$. Deduce that $S^{2}$ is not homeomorphic to any subset of $\mathbb{R}^{2}$.

  comment

• 3.II.20F

  Algebraic Topology

  Part II, 2008

  Let $X$ be the quotient space obtained by identifying one pair of antipodal points on $S^{2}$. Using the Mayer-Vietoris exact sequence, calculate the homology groups and the Betti numbers of $X$.

  comment

• 4.II.21F

  Algebraic Topology

  Part II, 2008

  Let $X$ and $Y$ be topological spaces.

  (i) Show that a map $f: X \rightarrow Y$ is a homotopy equivalence if there exist maps $g, h: Y \rightarrow X$ such that $f g \simeq 1_{Y}$ and $h f \simeq 1_{X}$. More generally, show that a map $f: X \rightarrow Y$ is a homotopy equivalence if there exist maps $g, h: Y \rightarrow X$ such that $f g$ and $h f$ are homotopy equivalences.

  (ii) Suppose that $\tilde{X}$ and $\tilde{Y}$ are universal covering spaces of the path-connected, locally path-connected spaces $X$ and $Y$. Using path-lifting properties, show that if $X \simeq Y$ then $\tilde{X} \simeq \tilde{Y}$.

  comment

• 1.II.22F

  Linear Analysis

  Part II, 2008

  Suppose $p$ and $q$ are real numbers with $p^{-1}+q^{-1}=1$ and $p, q>1$. Show, quoting any results on convexity that you need, that

  $$a^{1 / p} b^{1 / q} \leqslant \frac{a}{p}+\frac{b}{q}$$

  for all real positive $a$ and $b$.

  Define the space $l^{p}$ and show that it is a complete normed vector space.

  comment

• 2.II.22F

  Linear Analysis

  Part II, 2008

  State and prove the principle of uniform boundedness.

  [You may assume the Baire category theorem.]

  Suppose that $X, Y$ and $Z$ are Banach spaces. Suppose that

  $$F: X \times Y \rightarrow Z$$

  is linear and continuous in each variable separately, that is to say that, if $y$ is fixed,

  $$F(\cdot, y): X \rightarrow Z$$

  is a continuous linear map and, if $x$ is fixed,

  $$F(x, \cdot): Y \rightarrow Z$$

  is a continuous linear map. Show that there exists an $M$ such that

  $$\|F(x, y)\|_{Z} \leqslant M\|x\|_{X}\|y\|_{Y}$$

  for all $x \in X, y \in Y$. Deduce that $F$ is continuous.

  Suppose $X, Y, Z$ and $W$ are Banach spaces. Suppose that

  $$G: X \times Y \times W \rightarrow Z$$

  is linear and continuous in each variable separately. Does it follow that $G$ is continuous? Give reasons.

  Suppose that $X, Y$ and $Z$ are Banach spaces. Suppose that

  $$H: X \times Y \rightarrow Z$$

  is continuous in each variable separately. Does it follow that $H$ is continuous? Give reasons.

  comment

• 3.II.21F

  Linear Analysis

  Part II, 2008

  State and prove the Stone-Weierstrass theorem for real-valued functions. You may assume that the function $x \mapsto|x|$ can be uniformly approximated by polynomials on any interval $[-k, k]$.

  Suppose that $0<a<b<1$. Let $\mathcal{F}$ be the set of functions which can be uniformly approximated on $[a, b]$ by polynomials with integer coefficients. By making appropriate use of the identity

  $$\frac{1}{2}=\frac{x}{1-(1-2 x)}=\sum_{n=0}^{\infty} x(1-2 x)^{n}$$

  or otherwise, show that $\mathcal{F}=\mathcal{C}([a, b])$.

  Is it true that every continuous function on $[0, b]$ can be uniformly approximated by polynomials with integer coefficients?

  comment

• 4.II.22F

  Linear Analysis

  Part II, 2008

  Let $H$ be a Hilbert space. Show that if $V$ is a closed subspace of $H$ then any $f \in H$ can be written as $f=v+w$ with $v \in V$ and $w \perp V$.

  Suppose $U: H \rightarrow H$ is unitary (that is to say $U U^{*}=U^{*} U=I$ ). Let

  $$A_{n} f=\frac{1}{n} \sum_{k=0}^{n-1} U^{k} f$$

  and consider

  $$X=\{g-U g: g \in H\}$$

  (i) Show that $U$ is an isometry and $\left\|A_{n}\right\| \leqslant 1$.

  (ii) Show that $X$ is a subspace of $H$ and $A_{n} f \rightarrow 0$ as $n \rightarrow \infty$ whenever $f \in X$.

  (iii) Let $V$ be the closure of $X$. Show that $A_{n} v \rightarrow 0$ as $n \rightarrow \infty$ whenever $v \in V$.

  (iv) Show that, if $w \perp X$, then $U w=w$. Deduce that, if $w \perp V$, then $U w=w$.

  (v) If $f \in H$ show that there is a $w \in H$ such that $A_{n} f \rightarrow w$ as $n \rightarrow \infty$.

  comment

• 1.II.23H

  Riemann Surfaces

  Part II, 2008

  Define the terms Riemann surface, holomorphic map between Riemann surfaces and biholomorphic map.

  Show, without using the notion of degree, that a non-constant holomorphic map between compact connected Riemann surfaces must be surjective.

  Let $\phi$ be a biholomorphic map of the punctured unit disc $\Delta^{*}=\{0<|z|<1\} \subset \mathbb{C}$ onto itself. Show that $\phi$ extends to a biholomorphic map of the open unit disc $\Delta$ to itself such that $\phi(0)=0$.

  Suppose that $f: R \rightarrow S$ is a continuous holomorphic map between Riemann surfaces and $f$ is holomorphic on $R \backslash\{p\}$, where $p$ is a point in $R$. Show that $f$ is then holomorphic on all of $R$.

  [The Open Mapping Theorem may be used without proof if clearly stated.]

  comment

• 2.II.23H

  Riemann Surfaces

  Part II, 2008

  Explain what is meant by a divisor $D$ on a compact connected Riemann surface $S$. Explain briefly what is meant by a canonical divisor. Define the degree of $D$ and the notion of linear equivalence between divisors. If two divisors on $S$ have the same degree must they be linearly equivalent? Give a proof or a counterexample as appropriate, stating accurately any auxiliary results that you require.

  Define $\ell(D)$ for a divisor $D$, and state the Riemann-Roch theorem. Deduce that the dimension of the space of holomorphic differentials is determined by the genus $g$ of $S$ and that the same is true for the degree of a canonical divisor. Show further that if $g=2$ then $S$ admits a non-constant meromorphic function with at most two poles (counting with multiplicities).

  [General properties of meromorphic functions and meromorphic differentials on $S$ may be used without proof if clearly stated.]

  comment

• 3.II $. 22$

  Riemann Surfaces

  Part II, 2008

  Define the degree of a non-constant holomorphic map between compact connected Riemann surfaces and state the Riemann-Hurwitz formula.

  Show that there exists a compact connected Riemann surface of any genus $g \geqslant 0$.

  [You may use without proof any foundational results about holomorphic maps and complex algebraic curves from the course, provided that these are accurately stated. You may also assume that if $h(s)$ is a non-constant complex polynomial without repeated roots then the algebraic curve $C=\left\{(s, t) \in \mathbb{C}^{2}: t^{2}-h(s)=0\right\}$ is path connected.]

  comment

• $3 . \mathrm{II} . 12 \mathrm{~F}$

  Topics in Analysis

  Part II, 2008

  (a) State Liouville's theorem on approximation of algebraic numbers by rationals.

  (b) Consider the continued fraction expression

  $$x=a_{0}+\frac{1}{a_{1}+\frac{1}{a_{2}+\frac{1}{a_{3}+\ldots}}}$$

  in which the coefficients $a_{n}$ are all positive integers forming an unbounded set. Let $\frac{p_{n}}{q_{n}}$ be the $n$th convergent. Prove that

  $$\left|x-\frac{p_{n}}{q_{n}}\right| \leqslant \frac{1}{q_{n} q_{n+1}}$$

  and use this inequality together with Liouville's theorem to deduce that $x^{2}$ is irrational.

  [ You may assume without proof that, for $n=1,2,3, \ldots$,

  $$\left.\left(\begin{array}{ll} p_{n+1} & p_{n} \\ q_{n+1} & q_{n} \end{array}\right)=\left(\begin{array}{cc} p_{n} & p_{n-1} \\ q_{n} & q_{n-1} \end{array}\right)\left(\begin{array}{cc} a_{n+1} & 1 \\ 1 & 0 \end{array}\right) .\right]$$

  comment

• 4.II.23H

  Riemann Surfaces

  Part II, 2008

  Let $\Lambda$ be a lattice in $\mathbb{C}$ generated by 1 and $\tau$, where $\operatorname{Im} \tau>0$. The Weierstrass function $\wp$ is the unique meromorphic $\Lambda$-periodic function on $\mathbb{C}$, such that the only poles of $\wp$ are at points of $\Lambda$ and $\wp(z)-1 / z^{2} \rightarrow 0$ as $z \rightarrow 0$.

  Show that $\wp$ is an even function. Find all the zeroes of $\wp^{\prime}$.

  Suppose that $a$ is a complex number such that $2 a \notin \Lambda$. Show that the function

  $$h(z)=(\wp(z-a)-\wp(z+a))(\wp(z)-\wp(a))^{2}-\wp^{\prime}(z) \wp^{\prime}(a)$$

  has no poles in $\mathbb{C} \backslash \Lambda$. By considering the Laurent expansion of $h$ at $z=0$, or otherwise, deduce that $h$ is constant.

  [General properties of meromorphic doubly-periodic functions may be used without proof if accurately stated.]

  comment

• 1.II.24H

  Differential Geometry

  Part II, 2008

  Let $n \geqslant 1$ be an integer, and let $M(n)$ denote the set of $n \times n$ real-valued matrices. We make $M(n)$ into an $n^{2}$-dimensional smooth manifold via the obvious identification $M(n)=\mathbb{R}^{n^{2}}$.

  (a) Let $G L(n)$ denote the subset

  $$G L(n)=\left\{A \in M(n): A^{-1} \text { exists }\right\}$$

  Show that $G L(n)$ is a submanifold of $M(n)$. What is $\operatorname{dim} G L(n)$ ?

  (b) Now let $S L(n) \subset G L(n)$ denote the subset

  $$S L(n)=\{A \in G L(n): \operatorname{det} A=1\}$$

  Show that for $A \in G L(n)$,

  $$(d \text { det })_{A} B=\operatorname{tr}\left(A^{-1} B\right) \operatorname{det} A .$$

  Show that $S L(n)$ is a submanifold of $G L(n)$. What is the dimension of $S L(n) ?$

  (c) Now consider the set $X=M(n) \backslash G L(n)$. For what values of $n \geqslant 1$ is $X$ a submanifold of $M(n)$ ?

  comment

• 2.II $. 24 \mathrm{H}$

  Differential Geometry

  Part II, 2008

  (a) For a regular curve in $\mathbb{R}^{3}$, define curvature and torsion and state the Frenet formulas.

  (b) State and prove the isoperimetric inequality for domains $\Omega \subset \mathbb{R}^{2}$ with compact closure and $C^{1}$ boundary $\partial \Omega$.

  [You may assume Wirtinger's inequality.]

  (c) Let $\gamma: I \rightarrow \mathbb{R}^{2}$ be a closed plane regular curve such that $\gamma$ is contained in a disc of radius $r$. Show that there exists $s \in I$ such that $|k(s)| \geqslant r^{-1}$, where $k(s)$ denotes the signed curvature. Show by explicit example that the assumption of closedness is necessary.

  comment

• 3.II.23H

  Differential Geometry

  Part II, 2008

  Let $S \subset \mathbb{R}^{3}$ be a surface.

  (a) Define the Gauss Map, principal curvatures $k_{i}$, Gaussian curvature $K$ and mean curvature $H$. State the Theorema Egregium.

  (b) Define what is meant for $S$ to be minimal. Prove that if $S$ is minimal, then $K \leqslant 0$. Give an example of a minimal surface whose Gaussian curvature is not identically 0 , justifying your answer.

  (c) Does there exist a compact minimal surface $S \subset \mathbb{R}^{3}$ ? Justify your answer.

  comment

• 4.II $. 24 \mathrm{H} \quad$

  Differential Geometry

  Part II, 2008

  Let $S \subset \mathbb{R}^{3}$ be a surface.

  (a) In the case where $S$ is compact, define the Euler characteristic $\chi$ and genus $g$ of $S$.

  (b) Define the notion of geodesic curvature $k_{g}$ for regular curves $\gamma: I \rightarrow S$. When is $k_{g}=0$ ? State the Global Gauss-Bonnet Theorem (including boundary term).

  (c) Let $S=\mathbb{S}^{2}$ (the standard 2-sphere), and suppose $\gamma \subset \mathbb{S}^{2}$ is a simple closed regular curve such that $\mathbb{S}^{2} \backslash \gamma$ is the union of two distinct connected components with equal areas. Can $\gamma$ have everywhere strictly positive or everywhere strictly negative geodesic curvature?

  (d) Prove or disprove the following statement: if $S$ is connected with Gaussian curvature $K=1$ identically, then $S$ is a subset of a sphere of radius 1 .

  comment

• 1.II $. 25 \mathrm{~J} \quad$

  Probability and Measure

  Part II, 2008

  State the Dominated Convergence Theorem.

  Hence or otherwise prove Kronecker's Lemma: if $\left(a_{j}\right)$ is a sequence of non-negative reals such that

  $$\sum_{j=1}^{\infty} \frac{a_{j}}{j}<\infty$$

  then

  $$n^{-1} \sum_{j=1}^{n} a_{j} \rightarrow 0 \quad(n \rightarrow \infty)$$

  Let $\xi_{1}, \xi_{2}, \ldots$ be independent $N(0,1)$ random variables and set $S_{n}=\xi_{1}+\ldots+\xi_{n}$. Let $\mathcal{F}_{0}$ be the collection of all finite unions of intervals of the form $(a, b)$, where $a$ and $b$ are rational, together with the whole line $\mathbb{R}$. Prove that with probability 1 the limit

  $$m(B) \equiv \lim _{n \rightarrow \infty} \frac{1}{n} \sum_{j=1}^{n} I_{B}\left(S_{j}\right)$$

  exists for all $B \in \mathcal{F}_{0}$, and identify it. Is it possible to extend $m$ defined on $\mathcal{F}_{0}$ to a measure on the Borel $\sigma$-algebra of $\mathbb{R}$ ? Justify your answer.

  comment

• 2.II $. 25 J$

  Probability and Measure

  Part II, 2008

  Explain what is meant by a simple function on a measurable space $(S, \mathcal{S})$.

  Let $(S, \mathcal{S}, \mu)$ be a finite measure space and let $f: S \rightarrow \mathbb{R}$ be a non-negative Borel measurable function. State the definition of the integral of $f$ with respect to $\mu$.

  Prove that, for any sequence of simple functions $\left(g_{n}\right)$ such that $0 \leqslant g_{n}(x) \uparrow f(x)$ for all $x \in S$, we have

  $$\int g_{n} d \mu \uparrow \int f d \mu .$$

  State and prove the Monotone Convergence Theorem for finite measure spaces.

  comment

• $3 . \mathrm{II} . 24 \mathrm{~J} \quad$

  Probability and Measure

  Part II, 2008

  (i) What does it mean to say that a sequence of random variables $\left(X_{n}\right)$ converges in probability to $X$ ? What does it mean to say that the sequence $\left(X_{n}\right)$ converges in distribution to $X$ ? Prove that if $X_{n} \rightarrow X$ in probability, then $X_{n} \rightarrow X$ in distribution.

  (ii) What does it mean to say that a sequence of random variables $\left(X_{n}\right)$ is uniformly integrable? Show that, if $\left(X_{n}\right)$ is uniformly integrable and $X_{n} \rightarrow X$ in distribution, then $\mathbb{E}\left(X_{n}\right) \rightarrow \mathbb{E}(X)$.

  [Standard results from the course may be used without proof if clearly stated.]

  comment

• 4.II $. 25 \mathrm{~J}$

  Probability and Measure

  Part II, 2008

  (i) A stepfunction is any function $s$ on $\mathbb{R}$ which can be written in the form

  $$s(x)=\sum_{k=1}^{n} c_{k} I_{\left(a_{k}, b_{k}\right]}(x), \quad x \in \mathbb{R},$$

  where $a_{k}, b_{k}, c_{k}$ are real numbers, with $a_{k}<b_{k}$ for all $k$. Show that the set of all stepfunctions is dense in $L^{1}(\mathbb{R}, \mathcal{B}, \mu)$. Here, $\mathcal{B}$ denotes the Borel $\sigma$-algebra, and $\mu$ denotes Lebesgue measure.

  [You may use without proof the fact that, for any Borel set $B$ of finite measure, and any $\varepsilon>0$, there exists a finite union of intervals $A$ such that $\mu(A \triangle B)<\varepsilon$.]

  (ii) Show that the Fourier transform

  $$\hat{s}(t)=\int_{\mathbb{R}} s(x) e^{i t x} d x$$

  of a stepfunction has the property that $\hat{s}(t) \rightarrow 0$ as $|t| \rightarrow \infty$.

  (iii) Deduce that the Fourier transform of any integrable function has the same property.

  comment

• 1.II.26I

  Applied Probability

  Part II, 2008

  Let $\left(X_{t}, t \geqslant 0\right)$ be an irreducible continuous-time Markov chain with initial probability distribution $\pi$ and Q-matrix $Q$ (for short: a $(\pi, Q)$ CTMC), on a finite state space $I$.

  (i) Define the terms reversible CTMC and detailed balance equations (DBEs) and explain, without proof, the relation between them.

  (ii) Prove that any solution of the DBEs is an equilibrium distribution (ED) for $\left(X_{t}\right)$.

  Let $\left(Y_{n}, n=0,1, \ldots\right)$ be an irreducible discrete-time Markov chain with initial probability distribution $\widehat{\pi}$and transition probability matrix $\widehat{P}$(for short: a $(\widehat{\pi}, \widehat{P})$ DTMC), on the state space $I$.

  (iii) Repeat the two definitions from (i) in the context of the DTMC $\left(Y_{n}\right)$. State also in this context the relation between them, and prove a statement analogous to (ii).

  (iv) What does it mean to say that $\left(Y_{n}\right)$ is the jump chain for $\left(X_{t}\right)$ ? State and prove a relation between the ED $\pi$ for the $\operatorname{CTMC}\left(X_{t}\right)$ and the ED $\widehat{\pi}$for its jump chain $\left(Y_{n}\right)$.

  (v) Prove that $\left(X_{t}\right)$ is reversible (in equilibrium) if and only if its jump chain $\left(Y_{n}\right)$ is reversible (in equilibrium).

  (vi) Consider now a continuous time random walk on a graph. More precisely, consider a CTMC $\left(X_{t}\right)$ on an undirected graph, where some pairs of states $i, j \in I$ are joined by one or more non-oriented 'links' $e_{i j}(1), \ldots, e_{i j}\left(m_{i j}\right)$. Here $m_{i j}=m_{j i}$ is the number of links between $i$ and $j$. Assume that the jump rate $q_{i j}$ is proportional to $m_{i j}$. Can the chain $\left(X_{t}\right)$ be reversible? Identify the corresponding jump chain $\left(Y_{n}\right)$ (which determines a discrete-time random walk on the graph) and comment on its reversibility.

  comment