Let (Xt) be an irreducible continuous-time Markov chain with countably many states. What does it mean to say the chain is (i) positive recurrent, (ii) null recurrent? Consider the chain (Xt) with the arrow diagram below.
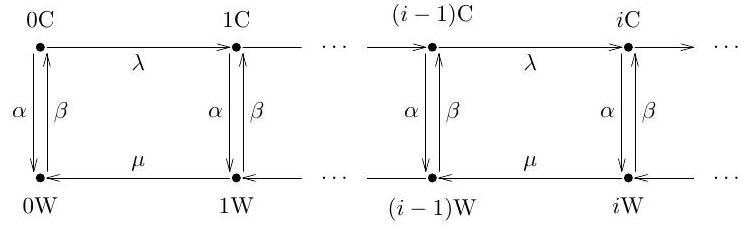
In this question we analyse the existence of equilibrium probabilities πiC and πi W of the chain (Xt) being in state iC or i W,i=0,1,…, and the impact of this fact on positive and null recurrence of the chain.
(a) Write down the invariance equations πQ=0 and check that they have the form
π0C(π1C,π1 W)(π(i+1)C,π(i+1)W)=λ+αβπ0 W,=λ+αβπ0 W(μ(λ+α)λ(μ+β),μλ)=(πiC,πi W)B,i=1,2,…,
where B is a 2×2 recursion matrix:
B=(μ(λ+α)λμ−βαμ(λ+α)β(β+μ)−μαμβ+μ)
(b) Verify that the row vector (π1C,π1 W) is an eigenvector of B with the eigenvalue θ where
θ=μ(λ+α)λ(μ+β)
Hence, specify the form of equilibrium probabilities πiC and πi W and conclude that the chain (Xt) is positive recurrent if and only if μα>λβ.
