3.II.27J
Part II, 2008
Consider a vector of asset prices evolving over time . The asset price is assumed constant over time. In this context, explain what is an arbitrage and prove that the existence of an equivalent martingale measure implies noarbitrage.
Suppose that over two periods a stock price moves on a binomial tree
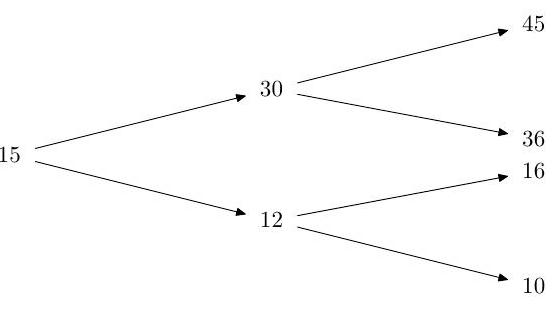
Assume riskless rate . Determine the equivalent martingale measure. [No proof is required.]
Sell an American put with strike 15 and expiry 2 at its no-arbitrage price, which you should determine.
Verify that the buyer of the option should use his early exercise right if the first period is bad.
Assume that the first period is bad, and that the buyer forgets to exercise. How much risk-free profit can you lock in?