Mathematics Tripos Papers

Paper 2, Section II, G

Algebraic Geometry

Part II, 2010

Let $X=X_{n, m, r}$ be the set of $n \times m$ matrices of rank at most $r$ over a field $k$ . Show that $X_{n, m, r}$ is naturally an affine subvariety of $\mathbf{A}^{n m}$ and that $X_{n, m, r}$ is a Zariski closed subvariety of $X_{n, m, r+1}$ .

Show that if $r<\min (n, m)$ , then 0 is a singular point of $X$ .

Determine the dimension of $X_{5,2,1}$ .

Paper 3, Section II, B

Part II, 2010

State Bloch's theorem for a one dimensional lattice which is invariant under translations by $a$ .

A simple model of a crystal consists of a one-dimensional linear array of identical sites with separation $a$ . At the $n$ th site the Hamiltonian, neglecting all other sites, is $H_{n}$ and an electron may occupy either of two states, $\phi_{n}(x)$ and $\chi_{n}(x)$ , where

H_{n} \phi_{n}(x)=E_{0} \phi_{n}(x), \quad H_{n} \chi_{n}(x)=E_{1} \chi_{n}(x),

and $\phi_{n}$ and $\chi_{n}$ are orthonormal. How are $\phi_{n}(x)$ and $\chi_{n}(x)$ related to $\phi_{0}(x)$ and $\chi_{0}(x)$ ?

The full Hamiltonian is $H$ and is invariant under translations by $a$ . Write trial wavefunctions $\psi(x)$ for the eigenstates of this model appropriate to a tight binding approximation if the electron has probability amplitudes $b_{n}$ and $c_{n}$ to be in the states $\phi_{n}$ and $\chi_{n}$ respectively.

Assume that the only non-zero matrix elements in this model are, for all $n$ ,

\begin{aligned} &\left(\phi_{n}, H_{n} \phi_{n}\right)=E_{0}, \quad\left(\chi_{n}, H_{n} \chi_{n}\right)=E_{1} \\ &\left(\phi_{n}, V \phi_{n \pm 1}\right)=\left(\chi_{n}, V \chi_{n \pm 1}\right)=\left(\phi_{n}, V \chi_{n \pm 1}\right)=\left(\chi_{n}, V \phi_{n \pm 1}\right)=-A, \end{aligned}

where $H=H_{n}+V$ and $A>0$ . Show that the time-dependent Schrödinger equation governing the amplitudes becomes

\begin{aligned} i \hbar \dot{b}_{n} &=E_{0} b_{n}-A\left(b_{n+1}+b_{n-1}+c_{n+1}+c_{n-1}\right) \\ i \hbar \dot{c}_{n} &=E_{1} c_{n}-A\left(c_{n+1}+c_{n-1}+b_{n+1}+b_{n-1}\right) \end{aligned}

By examining solutions of the form

\left(\begin{array}{l} b_{n} \\ c_{n} \end{array}\right)=\left(\begin{array}{l} B \\ C \end{array}\right) e^{i(k n a-E t / \hbar)}

show that the allowed energies of the electron are two bands given by

E=\frac{1}{2}\left(E_{0}+E_{1}-4 A \cos k a\right) \pm \frac{1}{2} \sqrt{\left(E_{0}-E_{1}\right)^{2}+16 A^{2} \cos ^{2} k a}

Define the Brillouin zone for this system and find the energies at the top and bottom of both bands. Hence, show that the energy gap between the bands is

\Delta E=-4 A+\sqrt{\left(E_{1}-E_{0}\right)^{2}+16 A^{2}}

Show that the wavefunctions $\psi(x)$ satisfy Bloch's theorem.

Describe briefly what are the crucial differences between insulators, conductors and semiconductors.

Paper 4, Section I, G

Part II, 2010

Let $p$ be a prime number, and put

a_{k}=k p, \quad N_{k}=a_{k}^{p}-1 \quad(k=1,2, \ldots)

Prove that $a_{k}$ has exact order $p$ modulo $N_{k}$ for all $k \geqslant 1$ , and deduce that $N_{k}$ must be divisible by a prime $q$ with $q \equiv 1 \quad(\bmod p)$ . By making a suitable choice of $k$ , prove that there are infinitely many primes $q$ with $q \equiv 1 \quad(\bmod p)$ .

Paper 3, Section II, G

Part II, 2010

State precisely the Miller-Rabin primality test.

(i) Let $p$ be a prime $\geqslant 5$ , and define

N=\frac{4^{p}-1}{3}

Prove that $N$ is a composite odd integer, and that $N$ is a pseudo-prime to the base 2 .

(ii) Let $M$ be an odd integer greater than 1 such that $M$ is a pseudo-prime to the base 2 . Prove that $2^{M}-1$ is always a strong pseudo-prime to the base 2 .

Paper 4, Section II, G

Part II, 2010

Let $\mathcal{S}$ be the set of all positive definite binary quadratic forms with integer coefficients. Define the action of the group $S L_{2}(\mathbb{Z})$ on $\mathcal{S}$ , and prove that equivalent forms under this action have the same discriminant.

Find necessary and sufficient conditions for an odd positive integer $n$ , prime to 35 , to be properly represented by at least one of the two forms

x^{2}+x y+9 y^{2}, \quad 3 x^{2}+x y+3 y^{2}

Paper 1, Section II, A

Part II, 2010

(a) State the Householder-John theorem and explain its relation to the convergence analysis of splitting methods for solving a system of linear equations $A x=b$ with a positive definite matrix $A$ .

(b) Describe the Jacobi method for solving a system $A x=b$ , and deduce from the above theorem that if $A$ is a symmetric positive definite tridiagonal matrix,

A=\left[\begin{array}{ccccc} a_{1} & c_{1} & & & \\ c_{1} & a_{2} & c_{2} & & \mathbf{0} \\ & \ddots & \ddots & \ddots & \\ \mathbf{0} & & c_{n-2} & a_{n-1} & c_{n-1} \\ & & & c_{n-1} & a_{n} \end{array}\right]

then the Jacobi method converges.

[Hint: At the last step, you may find it useful to consider two vectors $x=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ and $y=\left((-1) x_{1},(-1)^{2} x_{2}, \ldots,(-1)^{n} x_{n}\right)$ .]

Paper 2, Section II, A

Part II, 2010

The inverse discrete Fourier transform $\mathcal{F}_{n}^{-1}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is given by the formula

\mathbf{x}=\mathcal{F}_{n}^{-1} \mathbf{y}, \quad \text { where } \quad x_{\ell}=\sum_{j=0}^{n-1} \omega_{n}^{j \ell} y_{j}, \quad \ell=0, \ldots, n-1

Here, $\omega_{n}=\exp (2 \pi i / n)$ is the primitive root of unity of degree $n$ , and $n=2^{p}, p=1,2, \ldots$

(1) Show how to assemble $\mathbf{x}=\mathcal{F}_{2 m}^{-1} \mathbf{y}$ in a small number of operations if we already know the Fourier transforms of the even and odd portions of $\mathbf{y}$ :

\mathbf{x}^{(\mathrm{E})}=\mathcal{F}_{m}^{-1} \mathbf{y}^{(\mathrm{E})}, \quad \mathbf{x}^{(\mathrm{O})}=\mathcal{F}_{m}^{-1} \mathbf{y}^{(\mathrm{O})}

(2) Describe the Fast Fourier Transform (FFT) method for evaluating $\mathbf{x}$ and draw a relevant diagram for $n=8$ .

(3) Find the costs of the FFT for $n=2^{p}$ (only multiplications count).

(4) For $n=4$ , using the FFT technique, find $\mathbf{x}=\mathcal{F}_{4}^{-1} \mathbf{y}, \quad$ for $\quad \mathbf{y}=[1,1,-1,-1], \quad$ and $\quad \mathbf{y}=[1,-1,1,-1]$

Paper 3, Section II, A

Part II, 2010

The Poisson equation $\nabla^{2} u=f$ in the unit square $\Omega=[0,1] \times[0,1], u=0$ on $\partial \Omega$ , is discretized with the five-point formula

u_{i, j-1}+u_{i, j+1}+u_{i+1, j}+u_{i-1, j}-4 u_{i, j}=h^{2} f_{i, j}

where $1 \leqslant i, j \leqslant M, u_{i, j} \approx u(i h, j h)$ and $(i h, j h)$ are grid points.

Let $u(x, y)$ be the exact solution, and let $e_{i, j}=u_{i, j}-u(i h, j h)$ be the error of the five-point formula at the $(i, j)$ th grid point. Justifying each step, prove that

\|\mathbf{e}\|=\left[\sum_{i, j=1}^{M}\left|e_{i, j}\right|^{2}\right]^{1 / 2} \leqslant c h \quad \text { for sufficiently small } h>0,

where $c$ is some constant independent of $h$ .

Paper 4, Section II, A

Part II, 2010

An $s$ -stage explicit Runge-Kutta method of order $p$ , with constant step size $h>0$ , is applied to the differential equation $y^{\prime}=\lambda y, t \geqslant 0$ .

(a) Prove that

y_{n+1}=P_{s}(\lambda h) y_{n}

where $P_{s}$ is a polynomial of degree $s$ .

(b) Prove that the order $p$ of any $s$ -stage explicit Runge-Kutta method satisfies the inequality $p \leqslant s$ and, for $p=s$ , write down an explicit expression for $P_{s}$ .

(c) Prove that no explicit Runge-Kutta method can be A-stable.

Paper 2, Section II, J

Optimization and Control

Part II, 2010

(a) Suppose that

\left(\begin{array}{l} X \\ Y \end{array}\right) \sim N\left(\left(\begin{array}{l} \mu_{X} \\ \mu_{Y} \end{array}\right),\left(\begin{array}{ll} V_{X X} & V_{X Y} \\ V_{Y X} & V_{Y Y} \end{array}\right)\right)

Prove that conditional on $Y=y$ , the distribution of $X$ is again multivariate normal, with mean $\mu_{X}+V_{X Y} V_{Y Y}^{-1}\left(y-\mu_{Y}\right)$ and covariance $V_{X X}-V_{X Y} V_{Y Y}^{-1} V_{Y X}$ .

(b) The $\mathbb{R}^{d}$ -valued process $X$ evolves in discrete time according to the dynamics

X_{t+1}=A X_{t}+\varepsilon_{t+1}

where $A$ is a constant $d \times d$ matrix, and $\varepsilon_{t}$ are independent, with common $N\left(0, \Sigma_{\varepsilon}\right)$ distribution. The process $X$ is not observed directly; instead, all that is seen is the process $Y$ defined as

Y_{t}=C X_{t}+\eta_{t},

where $\eta_{t}$ are independent of each other and of the $\varepsilon_{t}$ , with common $N\left(0, \Sigma_{\eta}\right)$ distribution.

If the observer has the prior distribution $X_{0} \sim N\left(\hat{X}_{0}, V_{0}\right)$ for $X_{0}$ , prove that at all later times the distribution of $X_{t}$ conditional on $\mathcal{Y}_{t} \equiv\left(Y_{1}, \ldots, Y_{t}\right)$ is again normally distributed, with mean $\hat{X}_{t}$ and covariance $V_{t}$ which evolve as

\begin{aligned} \hat{X}_{t+1} &=A \hat{X}_{t}+M_{t} C^{T}\left(\Sigma_{\eta}+C M_{t} C^{T}\right)^{-1}\left(Y_{t+1}-C A \hat{X}_{t}\right) \\ V_{t+1} &=M_{t}-M_{t} C^{T}\left(\Sigma_{\eta}+C M_{t} C^{T}\right)^{-1} C M_{t} \end{aligned}

where

M_{t}=A V_{t} A^{T}+\Sigma_{\varepsilon}

(c) In the special case where both $X$ and $Y$ are one-dimensional, and $A=C=1$ , $\Sigma_{\varepsilon}=0$ , find the form of the updating recursion. Show in particular that

\frac{1}{V_{t+1}}=\frac{1}{V_{t}}+\frac{1}{\Sigma_{\eta}}

and that

\frac{\hat{X}_{t+1}}{V_{t+1}}=\frac{\hat{X}_{t}}{V_{t}}+\frac{Y_{t+1}}{\Sigma_{\eta}}

Hence deduce that, with probability one,

\lim _{t \rightarrow \infty} \hat{X}_{t}=\lim _{t \rightarrow \infty} t^{-1} \sum_{j=1}^{t} Y_{j}

Paper 3, Section II, J

Optimization and Control

Part II, 2010

Consider an infinite-horizon controlled Markov process having per-period costs $c(x, u) \geqslant 0$ , where $x \in \mathcal{X}$ is the state of the system, and $u \in \mathcal{U}$ is the control. Costs are discounted at rate $\beta \in(0,1]$ , so that the objective to be minimized is

\mathbb{E}\left[\sum_{t \geqslant 0} \beta^{t} c\left(X_{t}, u_{t}\right) \mid X_{0}=x\right]

What is meant by a policy $\pi$ for this problem?

Let $\mathcal{L}$ denote the dynamic programming operator

\mathcal{L} f(x) \equiv \inf _{u \in \mathcal{U}}\left\{c(x, u)+\beta \mathbb{E}\left[f\left(X_{1}\right) \mid X_{0}=x, u_{0}=u\right]\right\}

Further, let $F$ denote the value of the optimal control problem:

F(x)=\inf _{\pi} \mathbb{E}^{\pi}\left[\sum_{t \geqslant 0} \beta^{t} c\left(X_{t}, u_{t}\right) \mid X_{0}=x\right]

where the infimum is taken over all policies $\pi$ , and $\mathbb{E}^{\pi}$ denotes expectation under policy $\pi$ . Show that the functions $F_{t}$ defined by

F_{t+1}=\mathcal{L} F_{t} \quad(t \geqslant 0), \quad F_{0} \equiv 0

increase to a limit $F_{\infty} \in[0, \infty] .$ Prove that $F_{\infty} \leqslant F$ . Prove that $F=\mathcal{L} F$

Suppose that $\Phi=\mathcal{L} \Phi \geqslant 0$ . Prove that $\Phi \geqslant F$ .

[You may assume that there is a function $u_{*}: \mathcal{X} \rightarrow \mathcal{U}$ such that

\mathcal{L} \Phi(x)=c\left(x, u_{*}(x)\right)+\beta \mathbb{E}\left[\Phi\left(X_{1}\right) \mid X_{0}=x, u_{0}=u_{*}(x)\right]

though the result remains true without this simplifying assumption.]

Paper 4, Section II, J

Optimization and Control

Part II, 2010

Dr Seuss' wealth $x_{t}$ at time $t$ evolves as

\frac{d x}{d t}=r x_{t}+\ell_{t}-c_{t}

where $r>0$ is the rate of interest earned, $\ell_{t}$ is his intensity of working $(0 \leqslant \ell \leqslant 1)$ , and $c_{t}$ is his rate of consumption. His initial wealth $x_{0}>0$ is given, and his objective is to maximize

\int_{0}^{T} U\left(c_{t}, \ell_{t}\right) d t

where $U(c, \ell)=c^{\alpha}(1-\ell)^{\beta}$ , and $T$ is the (fixed) time his contract expires. The constants $\alpha$ and $\beta$ satisfy the inequalities $0<\alpha<1,0<\beta<1$ , and $\alpha+\beta>1$ . At all times, $c_{t}$ must be non-negative, and his final wealth $x_{T}$ must be non-negative. Establish the following properties of the optimal solution $\left(x^{*}, c^{*}, \ell^{*}\right)$ :

(i) $\beta c_{t}^{*}=\alpha\left(1-\ell_{t}^{*}\right)$ ;

(ii) $c_{t}^{*} \propto e^{-\gamma r t}$ , where $\gamma \equiv(\beta-1+\alpha)^{-1}$ ;

(iii) $x_{t}^{*}=A e^{r t}+B e^{-\gamma r t}-r^{-1}$ for some constants $A$ and $B$ .

Hence deduce that the optimal wealth is

x_{t}^{*}=\frac{\left(1-e^{-\gamma r T}\left(1+r x_{0}\right)\right) e^{r t}+\left(\left(1+r x_{0}\right) e^{r T}-1\right) e^{-\gamma r t}}{r\left(e^{r T}-e^{-\gamma r T}\right)}-\frac{1}{r}

Paper 4, Section II, B

Part II, 2010

The scattering amplitude for electrons of momentum $\hbar \mathbf{k}$ incident on an atom located at the origin is $f(\hat{\mathbf{r}})$ where $\hat{\mathbf{r}}=\mathbf{r} / r$ . Explain why, if the atom is displaced by a position vector a, the asymptotic form of the scattering wave function becomes

\psi_{\mathbf{k}}(\mathbf{r}) \sim e^{i \mathbf{k} \cdot \mathbf{r}}+e^{i \mathbf{k} \cdot \mathbf{a}} \frac{e^{i k r^{\prime}}}{r^{\prime}} f\left(\hat{\mathbf{r}}^{\prime}\right) \sim e^{i \mathbf{k} \cdot \mathbf{r}}+e^{i\left(\mathbf{k}-\mathbf{k}^{\prime}\right) \cdot \mathbf{a}} \frac{e^{i k r}}{r} f(\hat{\mathbf{r}}),

where $\mathbf{r}^{\prime}=\mathbf{r}-\mathbf{a}, r^{\prime}=\left|\mathbf{r}^{\prime}\right|, \hat{\mathbf{r}}^{\prime}=\mathbf{r}^{\prime} / r^{\prime}$ and $k=|\mathbf{k}|, \mathbf{k}^{\prime}=k \hat{\mathbf{r}}$ . For electrons incident on $N$ atoms in a regular Bravais crystal lattice show that the differential cross-section for scattering in the direction $\hat{\mathbf{r}}$ is

\frac{d \sigma}{d \Omega}=N|f(\hat{\mathbf{r}})|^{2} \Delta\left(\mathbf{k}-\mathbf{k}^{\prime}\right) .

Derive an explicit form for $\Delta(\mathbf{Q})$ and show that it is strongly peaked when $\mathbf{Q} \approx \mathbf{b}$ for $\mathbf{b}$ a reciprocal lattice vector.

State the Born approximation for $f(\hat{\mathbf{r}})$ when the scattering is due to a potential $V(\mathbf{r})$ . Calculate the Born approximation for the case $V(\mathbf{r})=-a \delta(\mathbf{r}) .$

Electrons with de Broglie wavelength $\lambda$ are incident on a target composed of many randomly oriented small crystals. They are found to be scattered strongly through an angle of $60^{\circ}$ . What is the likely distance between planes of atoms in the crystal responsible for the scattering?

Paper 1, Section II, E

Part II, 2010

(a) Solve by using the method of characteristics

x_{1} \frac{\partial}{\partial x_{1}} u+2 x_{2} \frac{\partial}{\partial x_{2}} u=5 u, \quad u\left(x_{1}, 1\right)=g\left(x_{1}\right),

where $g: \mathbb{R} \rightarrow \mathbb{R}$ is continuous. What is the maximal domain in $\mathbb{R}^{2}$ in which $u$ is a solution of the Cauchy problem?

(b) Prove that the function

u(x, t)=\left\{\begin{array}{cl} 0, & x<0, t>0 \\ x / t, & 0<x<t, t>0 \\ 1, & x>t>0 \end{array}\right.

is a weak solution of the Burgers equation

\frac{\partial}{\partial t} u+\frac{1}{2} \frac{\partial}{\partial x} u^{2}=0, \quad x \in \mathbb{R}, t>0

with initial data

u(x, 0)= \begin{cases}0, & x<0 \\ 1, & x>0\end{cases}

(c) Let $u=u(x, t), x \in \mathbb{R}, t>0$ be a piecewise $C^{1}$ -function with a jump discontinuity along the curve

\Gamma: x=s(t)

and let $u$ solve the Burgers equation $(*)$ on both sides of $\Gamma$ . Prove that $u$ is a weak solution of (1) if and only if

\dot{s}(t)=\frac{1}{2}\left(u_{l}(t)+u_{r}(t)\right)

holds, where $u_{l}(t), u_{r}(t)$ are the one-sided limits

u_{l}(t)=\lim _{x \nearrow_{s}(t)^{-}} u(x, t), \quad u_{r}(t)=\lim _{x \searrow s(t)^{+}} u(x, t)

[Hint: Multiply the equation by a test function $\phi \in C_{0}^{\infty}(\mathbb{R} \times[0, \infty))$ , split the integral appropriately and integrate by parts. Consider how the unit normal vector along $\Gamma$ can be expressed in terms of $\dot{s}$ .]

Paper 2, Section II, E

Part II, 2010

(a) State the Lax-Milgram lemma. Use it to prove that there exists a unique function $u$ in the space

H_{\partial}^{2}(\Omega)=\left\{u \in H^{2}(\Omega) ;\left.u\right|_{\partial \Omega}=\partial u /\left.\partial \gamma\right|_{\partial \Omega}=0\right\}

where $\Omega$ is a bounded domain in $\mathbb{R}^{n}$ with smooth boundary and $\gamma$ its outwards unit normal vector, which is the weak solution of the equations

\begin{aligned} \Delta^{2} u &=f \text { in } \Omega, \\ u &=\frac{\partial u}{\partial \gamma}=0 \text { on } \partial \Omega, \end{aligned}

for $f \in L^{2}(\Omega), \Delta$ the Laplacian and $\Delta^{2}=\Delta \Delta$ .

[Hint: Use regularity of the solution of the Dirichlet problem for the Poisson equation.]

(b) Let $\Omega \subset \mathbb{R}^{n}$ be a bounded domain with smooth boundary. Let $u \in H^{1}(\Omega)$ and denote

\bar{u}=\int_{\Omega} u d^{n} x / \int_{\Omega} d^{n} x

The following Poincaré-type inequality is known to hold

\|u-\bar{u}\|_{L^{2}} \leqslant C\|\nabla u\|_{L^{2}}

where $C$ only depends on $\Omega$ . Use the Lax-Milgram lemma and this Poincaré-type inequality to prove that the Neumann problem

\begin{aligned} &\Delta u=f \text { in } \Omega \\ &\frac{\partial u}{\partial \gamma}=0 \text { on } \partial \Omega \end{aligned}

has a unique weak solution in the space

H_{-}^{1}(\Omega)=H^{1}(\Omega) \cap\{u: \Omega \rightarrow \mathbb{R} ; \bar{u}=0\}

if and only if $\bar{f}=0$ .

Paper 3, Section II, 30E

Part II, 2010

Consider the Schrödinger equation

i \partial_{t} \Psi=-\frac{1}{2} \Delta \Psi, \quad x \in \mathbb{R}^{n}, t>0

for complex-valued solutions $\Psi(x, t)$ and where $\Delta$ is the Laplacian.

(a) Derive, by using a Fourier transform and its inversion, the fundamental solution of the Schrödinger equation. Obtain the solution of the initial value problem

\begin{aligned} i \partial_{t} \Psi=-\frac{1}{2} \Delta \Psi, & x \in \mathbb{R}^{n}, \quad t>0 \\ \Psi(x, 0)=f(x), & x \in \mathbb{R}^{n} \end{aligned}

as a convolution.

(b) Consider the Wigner-transform of the solution of the Schrödinger equation

w(x, \xi, t)=\frac{1}{(2 \pi)^{n}} \int_{\mathbb{R}^{n}} \Psi\left(x+\frac{1}{2} y, t\right) \bar{\Psi}\left(x-\frac{1}{2} y, t\right) e^{-i y \cdot \xi} \mathrm{d}^{n} y

defined for $x \in \mathbb{R}^{n}, \xi \in \mathbb{R}^{n}, t>0$ . Derive an evolution equation for $w$ by using the Schrödinger equation. Write down the solution of this evolution equation for given initial data $w(x, \xi, 0)=g(x, \xi)$ .

Paper 4, Section II, 30E

Part II, 2010

a) Solve the Dirichlet problem for the Laplace equation in a disc in $\mathbb{R}^{2}$

\begin{aligned} \Delta u &=0 \quad \text { in } \quad G=\left\{x^{2}+y^{2}<R^{2}\right\} \subseteq \mathbb{R}^{2}, R>0 \\ u &=u_{D} \quad \text { on } \quad \partial G \end{aligned}

using polar coordinates $(r, \varphi)$ and separation of variables, $u(x, y)=R(r) \Theta(\varphi)$ . Then use the ansatz $R(r)=r^{\alpha}$ for the radial function.

b) Solve the Dirichlet problem for the Laplace equation in a square in $\mathbb{R}^{2}$

\begin{aligned} &\Delta u=0 \quad \text { in } \quad G=[0, a] \times[0, a] \\ &u(x, 0)=f_{1}(x), \quad u(x, a)=f_{2}(x), \quad u(0, y)=f_{3}(y), \quad u(a, y)=f_{4}(y) \end{aligned}

Paper 1, Section II, C

Part II, 2010

Two states $\left|j_{1} m_{1}\right\rangle_{1},\left|j_{2} m_{2}\right\rangle_{2}$ , with angular momenta $j_{1}, j_{2}$ , are combined to form states $|J M\rangle$ with total angular momentum

J=\left|j_{1}-j_{2}\right|,\left|j_{1}-j_{2}\right|+1, \ldots, j_{1}+j_{2} .

Write down the state with $J=M=j_{1}+j_{2}$ in terms of the original angular momentum states. Briefly describe how the other combined angular momentum states may be found in terms of the original angular momentum states.

If $j_{1}=j_{2}=j$ , explain why the state with $J=0$ must be of the form

|00\rangle=\sum_{m=-j}^{j} \alpha_{m}|j m\rangle_{1}|j-m\rangle_{2}

By considering $J_{+}|00\rangle$ , determine a relation between $\alpha_{m+1}$ and $\alpha_{m}$ , hence find $\alpha_{m}$ .

If the system is in the state $|j j\rangle_{1}|j-j\rangle_{2}$ what is the probability, written in terms of $j$ , of measuring the combined total angular momentum to bero?

[Standard angular momentum states $|j m\rangle$ are joint eigenstates of $\mathbf{J}^{2}$ and $J_{3}$ , obeying

J_{\pm}|j m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j m \pm 1\rangle

Units in which $\hbar=1$ have been used throughout.]

Paper 2, Section II, C

Part II, 2010

Consider a joint eigenstate of $\mathbf{J}^{2}$ and $J_{3},|j m\rangle$ . Write down a unitary operator $U(\mathbf{n}, \theta)$ for rotation of the state by an angle $\theta$ about an axis with direction $\mathbf{n}$ , where $\mathbf{n}$ is a unit vector. How would a state with zero orbital angular momentum transform under such a rotation?

What is the relation between the angular momentum operator $\mathbf{J}$ and the Pauli matrices $\boldsymbol{\sigma}$ when $j=\frac{1}{2}$ ? Explicitly calculate $(\mathbf{J} \cdot \mathbf{a})^{2}$ , for an arbitrary real vector $\mathbf{a}$ , in this case. What are the eigenvalues of the operator $\mathbf{J} \cdot \mathbf{a}$ ? Show that the unitary rotation operator for $j=\frac{1}{2}$ can be expressed as

U(\mathbf{n}, \theta)=\cos \frac{\theta}{2}-i \mathbf{n} \cdot \boldsymbol{\sigma} \sin \frac{\theta}{2}

Starting with a state $\left|\frac{1}{2} m\right\rangle$ the component of angular momentum along a direction $\mathbf{n}^{\prime}$ , making and angle $\theta$ with the $z$ -axis, is susequently measured to be $m^{\prime}$ . Immediately after this measurement the state is $\left|\frac{1}{2} m^{\prime}\right\rangle_{\theta}$ . Write down an eigenvalue equation for $\left|\frac{1}{2} m^{\prime}\right\rangle_{\theta}$ in terms of $\mathbf{n}^{\prime} \cdot \mathbf{J}$ . Show that the probability for measuring an angular momentum of $m^{\prime} \hbar$ along the direction $\mathbf{n}^{\prime}$ is, assuming $\mathbf{n}^{\prime}$ is in the $x-z$ plane,

\left|\left\langle\frac{1}{2} m \mid \frac{1}{2} m^{\prime}\right\rangle_{\theta}\right|^{2}=\left|\left\langle\frac{1}{2} m|U(\mathbf{y}, \theta)| \frac{1}{2} m^{\prime}\right\rangle\right|^{2},

where $\mathbf{y}$ is a unit vector in the $y$ -direction. Using $(*)$ show that the probability that $m=+\frac{1}{2}, m^{\prime}=-\frac{1}{2}$ is of the form

A+B \cos ^{2} \frac{\theta}{2}

determining the integers $A$ and $B$ in the process.

[Assume $\hbar=1$ . The Pauli matrices are

\sigma_{1}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{rr} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array}\right)

Paper 3, Section II, C

Part II, 2010

What are the commutation relations between the position operator $\hat{x}$ and momentum operator $\hat{p}$ ? Show that this is consistent with $\hat{x}, \hat{p}$ being hermitian.

The annihilation operator for a harmonic oscillator is

a=\sqrt{\frac{1}{2 \hbar}}(\hat{x}+i \hat{p})

in units where the mass and frequency of the oscillator are 1 . Derive the relation $\left[a, a^{\dagger}\right]=1$ . Write down an expression for the Hamiltonian

H=\frac{1}{2} \hat{p}^{2}+\frac{1}{2} \hat{x}^{2}

in terms of the operator $N=a^{\dagger} a$ .

Assume there exists a unique ground state $|0\rangle$ of $H$ such that $a|0\rangle=0$ . Explain how the space of eigenstates $|n\rangle$ , is formed, and deduce the energy eigenvalues for these states. Show that

a|n\rangle=A|n-1\rangle, \quad a^{\dagger}|n\rangle=B|n+1\rangle

finding $A$ and $B$ in terms of $n$ .

Calculate the energy eigenvalues of the Hamiltonian for two harmonic oscillators

H=H_{1}+H_{2}, \quad H_{i}=\frac{1}{2} \hat{p}_{i}^{2}+\frac{1}{2} \hat{x}_{i}^{2}, \quad i=1,2 .

What is the degeneracy of the $n^{\text {th }}$ energy level? Suppose that the two oscillators are then coupled by adding the extra term

\Delta H=\lambda \hat{x}_{1} \hat{x}_{2}

to $H$ , where $\lambda \ll 1$ . Calculate the energies for the states of the unperturbed system with the three lowest energy eigenvalues to first order in $\lambda$ using perturbation theory.

[You may assume standard perturbation theory results.]

Paper 4, Section II, C

Part II, 2010

The Hamiltonian for a quantum system in the Schrödinger picture is

H_{0}+V(t)

where $H_{0}$ is independent of time. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.

Let $|a\rangle$ and $|b\rangle$ be orthonormal eigenstates of $H_{0}$ with eigenvalues $E_{a}$ and $E_{b}$ respectively. Assume $V(t)=0$ for $t \leqslant 0$ . Show that if the system is initially, at $t=0$ , in the state $|a\rangle$ then the probability of measuring it to be the state $|b\rangle$ after a time $t$ is

\frac{1}{\hbar^{2}}\left|\int_{0}^{t} d t^{\prime}\left\langle b\left|V\left(t^{\prime}\right)\right| a\right\rangle e^{i\left(E_{b}-E_{a}\right) t^{\prime} / \hbar}\right|^{2}

to order $V(t)^{2}$ .

Suppose a system has a basis of just two orthonormal states $|1\rangle$ and $|2\rangle$ , with respect to which

H_{0}=E I, \quad V(t)=v t \sigma_{1}, \quad t \geqslant 0,

where

I=\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right), \quad \sigma_{1}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right)

Use $(*)$ to calculate the probability of a transition from state $|1\rangle$ to state $|2\rangle$ after a time $t$ to order $v^{2}$ .

Show that the time dependent Schrödinger equation has a solution

|\psi(t)\rangle=\exp \left(-\frac{i}{\hbar}\left(E t I+\frac{1}{2} v t^{2} \sigma_{1}\right)\right)|\psi(0)\rangle

Calculate the transition probability exactly. Hence find the condition for the order $v^{2}$ approximation to be valid.

Paper 1, Section II, J

Part II, 2010

The distribution of a random variable $X$ is obtained from the binomial distribution $\mathcal{B}(n ; \Pi)$ by conditioning on $X>0$ ; here $\Pi \in(0,1)$ is an unknown probability parameter and $n$ is known. Show that the distributions of $X$ form an exponential family and identify the natural sufficient statistic $T$ , natural parameter $\Phi$ , and cumulant function $k(\phi)$ . Using general properties of the cumulant function, compute the mean and variance of $X$ when $\Pi=\pi$ . Write down an equation for the maximum likelihood estimate $\widehat{\Pi}$ of $\Pi$ and explain why, when $\Pi=\pi$ , the distribution of $\widehat{\Pi}$ is approximately normal $\mathcal{N}(\pi, \pi(1-\pi) / n)$ for large $n$ .

Suppose we observe $X=1$ . It is suggested that, since the condition $X>0$ is then automatically satisfied, general principles of inference require that the inference to be drawn should be the same as if the distribution of $X$ had been $\mathcal{B}(n ; \Pi)$ and we had observed $X=1$ . Comment briefly on this suggestion.

Paper 2, Section II, J

Part II, 2010

Define the Kolmogorov-Smirnov statistic for testing the null hypothesis that real random variables $X_{1}, \ldots, X_{n}$ are independently and identically distributed with specified continuous, strictly increasing distribution function $F$ , and show that its null distribution does not depend on $F$ .

A composite hypothesis $H_{0}$ specifies that, when the unknown positive parameter $\Theta$ takes value $\theta$ , the random variables $X_{1}, \ldots, X_{n}$ arise independently from the uniform distribution $\mathrm{U}[0, \theta]$ . Letting $J:=\arg \max _{1 \leqslant i \leqslant n} X_{i}$ , show that, under $H_{0}$ , the statistic $\left(J, X_{J}\right)$ is sufficient for $\Theta$ . Show further that, given $\left\{J=j, X_{j}=\xi\right\}$ , the random variables $\left(X_{i}: i \neq j\right)$ are independent and have the $\mathrm{U}[0, \xi]$ distribution. How might you apply the Kolmogorov-Smirnov test to test the hypothesis $H_{0}$ ?

Paper 1, Section II, I

Part II, 2010

(a) Define what it means to say that $\pi$ is an equilibrium distribution for a Markov chain on a countable state space with Q-matrix $Q=\left(q_{i j}\right)$ , and give an equation which is satisfied by any equilibrium distribution. Comment on the possible non-uniqueness of equilibrium distributions.

(b) State a theorem on convergence to an equilibrium distribution for a continuoustime Markov chain.

A continuous-time Markov chain $\left(X_{t}, t \geqslant 0\right)$ has three states $1,2,3$ and the Qmatrix $Q=\left(q_{i j}\right)$ is of the form

Q=\left(\begin{array}{ccc} -\lambda_{1} & \lambda_{1} / 2 & \lambda_{1} / 2 \\ \lambda_{2} / 2 & -\lambda_{2} & \lambda_{2} / 2 \\ \lambda_{3} / 2 & \lambda_{3} / 2 & -\lambda_{3} \end{array}\right)

where the rates $\lambda_{1}, \lambda_{2}, \lambda_{3} \in[0, \infty)$ are not all zero.

[Note that some of the $\lambda_{i}$ may be zero, and those cases may need special treatment.]

(c) Find the equilibrium distributions of the Markov chain in question. Specify the cases of uniqueness and non-uniqueness.

(d) Find the limit of the transition matrix $P(t)=\exp (t Q)$ when $t \rightarrow \infty$ .

(e) Describe the jump chain $\left(Y_{n}\right)$ and its equilibrium distributions. If $\widehat{P}$ is the jump probability matrix, find the limit of $\widehat{P}^{n}$ as $n \rightarrow \infty$ .

Paper 3, Section II, $\mathbf{2 7 J}$

Part II, 2010

Define the normal and extensive form solutions of a Bayesian statistical decision problem involving parameter $\Theta$ , random variable $X$ , and loss function $L(\theta, a)$ . How are they related? Let $R_{0}=R_{0}(\Pi)$ be the Bayes loss of the optimal act when $\Theta \sim \Pi$ and no data can be observed. Express the Bayes risk $R_{1}$ of the optimal statistical decision rule in terms of $R_{0}$ and the joint distribution of $(\Theta, X)$ .

The real parameter $\Theta$ has distribution $\Pi$ , having probability density function $\pi(\cdot)$ . Consider the problem of specifying a set $S \subseteq \mathbb{R}$ such that the loss when $\Theta=\theta$ is $L(\theta, S)=c|S|-\mathbf{1}_{S}(\theta)$ , where $\mathbf{1}_{S}$ is the indicator function of $S$ , where $c>0$ , and where $|S|=\int_{S} d x$ . Show that the "highest density" region $S^{*}:=\{\theta: \pi(\theta) \geqslant c\}$ supplies a Bayes act for this decision problem, and explain why $R_{0}(\Pi) \leqslant 0$ .

For the case $\Theta \sim \mathcal{N}\left(\mu, \sigma^{2}\right)$ , find an expression for $R_{0}$ in terms of the standard normal distribution function $\Phi$ .

Suppose now that $c=0.5$ , that $\Theta \sim \mathcal{N}(0,1)$ and that $X \mid \Theta \sim \mathcal{N}(\Theta, 1 / 9)$ . Show that $R_{1}<R_{0}$ .

Paper 4, Section II, $\mathbf{2 7 J}$

Part II, 2010

Define completeness and bounded completeness of a statistic $T$ in a statistical experiment.

Random variables $X_{1}, X_{2}, X_{3}$ are generated as $X_{i}=\Theta^{1 / 2} Z+(1-\Theta)^{1 / 2} Y_{i}$ , where $Z, Y_{1}, Y_{2}, Y_{3}$ are independently standard normal $\mathcal{N}(0,1)$ , and the parameter $\Theta$ takes values in $(0,1)$ . What is the joint distribution of $\left(X_{1}, X_{2}, X_{3}\right)$ when $\Theta=\theta$ ? Write down its density function, and show that a minimal sufficient statistic for $\Theta$ based on $\left(X_{1}, X_{2}, X_{3}\right)$ is $T=\left(T_{1}, T_{2}\right):=\left(\sum_{i=1}^{3} X_{i}^{2},\left(\sum_{i=1}^{3} X_{i}\right)^{2}\right)$ .

[Hint: You may use that if $I$ is the $n \times n$ identity matrix and $J$ is the $n \times n$ matrix all of whose entries are 1 , then $a I+b J$ has determinant $a^{n-1}(a+n b)$ , and inverse $c I+d J$ with $c=1 / a, d=-b /(a(a+n b))$ .]

What is $\mathbb{E}_{\theta}\left(T_{1}\right) ?$ Is $T$ complete for $\Theta ?$

Let $S:=\operatorname{Prob}\left(X_{1}^{2} \leqslant 1 \mid T\right)$ . Show that $\mathbb{E}_{\theta}(S)$ is a positive constant $c$ which does not depend on $\theta$ , but that $S$ is not identically equal to $c$ . Is $T$ boundedly complete for $\Theta$ ?

Paper 1, Section II, I

Part II, 2010

State Carathéodory's extension theorem. Define all terms used in the statement.

Let $\mathcal{A}$ be the ring of finite unions of disjoint bounded intervals of the form

A=\bigcup_{i=1}^{m}\left(a_{i}, b_{i}\right]

where $m \in \mathbb{Z}^{+}$ and $a_{1}<b_{1}<\ldots<a_{m}<b_{m}$ . Consider the set function $\mu$ defined on $\mathcal{A}$ by

\mu(A)=\sum_{i=1}^{m}\left(b_{i}-a_{i}\right)

You may assume that $\mu$ is additive. Show that for any decreasing sequence $\left(B_{n}: n \in \mathbb{N}\right)$ in $\mathcal{A}$ with empty intersection we have $\mu\left(B_{n}\right) \rightarrow 0$ as $n \rightarrow \infty$ .

Explain how this fact can be used in conjunction with Carathéodory's extension theorem to prove the existence of Lebesgue measure.

Paper 2, Section II, I

Part II, 2010

Show that any two probability measures which agree on a $\pi$ -system also agree on the $\sigma$ -algebra generated by that $\pi$ -system.

State Fubini's theorem for non-negative measurable functions.

Let $\mu$ denote Lebesgue measure on $\mathbb{R}^{2}$ . Fix $s \in[0,1)$ . Set $c=\sqrt{1-s^{2}}$ and $\lambda=\sqrt{c}$ . Consider the linear maps $f, g, h: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ given by

f(x, y)=\left(\lambda^{-1} x, \lambda y\right), \quad g(x, y)=(x, s x+y), \quad h(x, y)=(x-s y, y)

Show that $\mu=\mu \circ f^{-1}$ and that $\mu=\mu \circ g^{-1}$ . You must justify any assertion you make concerning the values taken by $\mu$ .

Compute $r=f \circ h \circ g \circ f$ . Deduce that $\mu$ is invariant under rotations.

Paper 3, Section II, I

Part II, 2010

Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent random variables with common density function

f(x)=\frac{1}{\pi\left(1+x^{2}\right)}

Fix $\alpha \in[0,1]$ and set

Y_{n}=\operatorname{sgn}\left(X_{n}\right)\left|X_{n}\right|^{\alpha}, \quad S_{n}=Y_{1}+\ldots+Y_{n}

Show that for all $\alpha \in[0,1]$ the sequence of random variables $S_{n} / n$ converges in distribution and determine the limit.

[Hint: In the case $\alpha=1$ it may be useful to prove that $\mathbb{E}\left(e^{i u X_{1}}\right)=e^{-|u|}$ , for all $\left.u \in \mathbb{R} .\right]$

Show further that for all $\alpha \in[0,1 / 2)$ the sequence of random variables $S_{n} / \sqrt{n}$ converges in distribution and determine the limit.

[You should state clearly any result about random variables from the course to which you appeal. You are not expected to evaluate explicitly the integral

m(\alpha)=\int_{0}^{\infty} \frac{x^{\alpha}}{\pi\left(1+x^{2}\right)} d x

Paper 4, Section II, I

Part II, 2010

Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent normal random variables having mean 0 and variance 1 . Set $S_{n}=X_{1}+\ldots+X_{n}$ and $U_{n}=S_{n}-\left\lfloor S_{n}\right\rfloor$ . Thus $U_{n}$ is the fractional part of $S_{n}$ . Show that $U_{n}$ converges to $U$ in distribution, as $n \rightarrow \infty$ where $U$ is uniformly distributed on $[0,1]$ .

Paper 1, Section II, F

Part II, 2010

(i) Let $N$ be a normal subgroup of the finite group $G$ . Without giving detailed proofs, define the process of lifting characters from $G / N$ to $G$ . State also the orthogonality relations for $G$ .

(ii) Let $a, b$ be the following two permutations in $S_{12}$ ,

and let $G=\langle a, b\rangle$ , a subgroup of $S_{12}$ . Prove that $G$ is a group of order 12 and list the conjugacy classes of $G$ . By identifying a normal subgroup of $G$ of index 4 and lifting irreducible characters, calculate all the linear characters of $G$ . Calculate the complete character table of $G$ . By considering 6 th roots of unity, find explicit matrix representations affording the non-linear characters of $G$ .

Paper 2, Section II, F

Part II, 2010

Define the concepts of induction and restriction of characters. State and prove the Frobenius Reciprocity Theorem.

Let $H$ be a subgroup of $G$ and let $g \in G$ . We write $\mathcal{C}(g)$ for the conjugacy class of $g$ in $G$ , and write $C_{G}(g)$ for the centraliser of $g$ in $G$ . Suppose that $H \cap \mathcal{C}(g)$ breaks up into $m$ conjugacy classes of $H$ , with representatives $x_{1}, x_{2}, \ldots, x_{m}$ .

Let $\psi$ be a character of $H$ . Writing $\operatorname{Ind}_{H}^{G}(\psi)$ for the induced character, prove that

(i) if no element of $\mathcal{C}(g)$ lies in $H$ , then $\operatorname{Ind}_{H}^{G}(\psi)(g)=0$ ,

(ii) if some element of $\mathcal{C}(g)$ lies in $H$ , then

\operatorname{Ind}_{H}^{G}(\psi)(g)=\left|C_{G}(g)\right| \sum_{i=1}^{m} \frac{\psi\left(x_{i}\right)}{\left|C_{H}\left(x_{i}\right)\right|} .

Let $G=S_{4}$ and let $H=\langle a, b\rangle$ , where $a=\left(\begin{array}{llll}1 & 2 & 3 & 4\end{array}\right)$ and $b=\left(\begin{array}{l}1\end{array}\right.$ dihedral group and write down its character table. Restrict each $G$ -conjugacy class to $H$ and calculate the $H$ -conjugacy classes contained in each restriction. Given a character $\psi$ of $H$ , express Ind ${ }_{H}^{G}(\psi)(g)$ in terms of $\psi$ , where $g$ runs through a set of conjugacy classes of $G$ . Use your calculation to find the values of all the irreducible characters of $H$ induced to $G$ .

\begin{aligned} & a=\left(\begin{array}{lllll}1 & 2 & 3 & 5 & 6\end{array}\right)(789101112), \\ & b=\left(\begin{array}{llll}1 & 7 & 4 & 10\end{array}\right)\left(\begin{array}{llll}2 & 12 & 5 & 9\end{array}\right)(368), \end{aligned}

Paper 3, Section II, F

Part II, 2010

Show that the degree of a complex irreducible character of a finite group is a factor of the order of the group.

State and prove Burnside's $p^{a} q^{b}$ theorem. You should quote clearly any results you use.

Prove that for any group of odd order $n$ having precisely $k$ conjugacy classes, the integer $n-k$ is divisible by 16 .

Paper 4, Section II, F

Part II, 2010

Define the circle group $U(1)$ . Give a complete list of the irreducible representations of $U(1)$

Define the spin group $G=S U(2)$ , and explain briefly why it is homeomorphic to the unit 3-sphere in $\mathbb{R}^{4}$ . Identify the conjugacy classes of $G$ and describe the classification of the irreducible representations of $G$ . Identify the characters afforded by the irreducible representations. You need not give detailed proofs but you should define all the terms you use.

Let $G$ act on the space $\mathrm{M}_{3}(\mathbb{C})$ of $3 \times 3$ complex matrices by conjugation, where $A \in S U(2)$ acts by

A: M \mapsto A_{1} M A_{1}^{-1}

in which $A_{1}$ denotes the $3 \times 3$ block diagonal matrix $\left(\begin{array}{cc}A & 0 \\ 0 & 1\end{array}\right)$ . Show that this gives a representation of $G$ and decompose it into irreducibles.

Paper 2, Section II, I

Part II, 2010

(a) Let $S_{k}$ be the sum of $k$ independent exponential random variables of rate $k \mu$ . Compute the moment generating function $\phi_{S_{k}}(\theta)=\mathbb{E} e^{\theta S_{k}}$ of $S_{k}$ . Show that, as $k \rightarrow \infty$ , functions $\phi_{S_{k}}(\theta)$ converge to a limit. Describe the random variable $S$ for which the limiting function $\lim _{k \rightarrow \infty} \phi_{S_{k}}(\theta)$ coincides with $\mathbb{E} e^{\theta S}$ .

(b) Define the $M / G / 1$ queue with infinite capacity (sometimes written $M / G / 1 / \infty$ ). Introduce the embedded discrete-time Markov chain $\left(X_{n}\right)$ and write down the recursive relation between $X_{n}$ and $X_{n-1}$ .

Consider, for each fixed $k$ and for $0<\lambda<\mu$ , an $\mathrm{M} / \mathrm{G} / 1 / \infty$ queue with arrival rate $\lambda$ and with service times distributed as $S_{k}$ . Assume that the queue is empty at time 0 . Let $T_{k}$ be the earliest time at which a customer departs leaving the queue empty. Let $A$ be the first arrival time and $B_{k}=T_{k}-A$ the length of the busy period.

(c) Prove that the moment generating functions $\phi_{B_{k}}(\theta)=\mathbb{E} e^{\theta B_{k}}$ and $\phi_{S_{k}}(\theta)$ are related by the equation

\phi_{B_{k}}(\theta)=\phi_{S_{k}}\left(\theta-\lambda\left(1-\phi_{B_{k}}(\theta)\right)\right)

(d) Prove that the moment generating functions $\phi_{T_{k}}(\theta)=\mathbb{E} e^{\theta T_{k}}$ and $\phi_{S_{k}}(\theta)$ are related by the equation

\frac{\lambda-\theta}{\lambda} \phi_{T_{k}}(\theta)=\phi_{S_{k}}\left((\lambda-\theta)\left(\phi_{T_{k}}(\theta)-1\right)\right)

(e) Assume that, for all $\theta<\lambda$ ,

\lim _{k \rightarrow \infty} \phi_{B_{k}}(\theta)=\mathbb{E} e^{\theta B}, \quad \lim _{k \rightarrow \infty} \phi_{T_{k}}(\theta)=\mathbb{E} e^{\theta T},

for some random variables $B$ and $T$ . Calculate $\mathbb{E} B$ and $\mathbb{E} T$ . What service time distribution do these values correspond to?

Paper 1, Section II, G

Riemann Surfaces

Part II, 2010

Given a lattice $\Lambda \subset \mathbb{C}$ , we may define the corresponding Weierstrass $\wp$ -function to be the unique even $\Lambda$ -periodic elliptic function $\wp$ with poles only on $\Lambda$ and for which $\wp(z)-1 / z^{2} \rightarrow 0$ as $z \rightarrow 0$ . For $w \notin \Lambda$ , we set

f(z)=\operatorname{det}\left(\begin{array}{ccc} 1 & 1 & 1 \\ \wp(z) & \wp(w) & \wp(-z-w) \\ \wp^{\prime}(z) & \wp^{\prime}(w) & \wp^{\prime}(-z-w) \end{array}\right)

an elliptic function with periods $\Lambda$ . By considering the poles of $f$ , show that $f$ has valency at most 4 (i.e. is at most 4 to 1 on a period parallelogram).

If $w \notin \frac{1}{3} \Lambda$ , show that $f$ has at least six distinct zeros. If $w \in \frac{1}{3} \Lambda$ , show that $f$ has at least four distinct zeros, at least one of which is a multiple zero. Deduce that the meromorphic function $f$ is identically zero.

If $z_{1}, z_{2}, z_{3}$ are distinct non-lattice points in a period parallelogram such that $z_{1}+z_{2}+z_{3} \in \Lambda$ , what can be said about the points $\left(\wp\left(z_{i}\right), \wp^{\prime}\left(z_{i}\right)\right) \in \mathbb{C}^{2}(i=1,2,3) ?$

Paper 2, Section II, G

Riemann Surfaces

Part II, 2010

Given a complete analytic function $\mathcal{F}$ on a domain $U \subset \mathbb{C}$ , describe briefly how the space of germs construction yields a Riemann surface $R$ associated to $\mathcal{F}$ together with a covering map $\pi: R \rightarrow U$ (proofs not required).

In the case when $\pi$ is regular, explain briefly how, given a point $P \in U$ , any closed curve in $U$ with initial and final points $P$ yields a permutation of the set $\pi^{-1}(P)$ .

Now consider the Riemann surface $R$ associated with the complete analytic function

\left(z^{2}-1\right)^{1 / 2}+\left(z^{2}-4\right)^{1 / 2}

on $U=\mathbb{C} \backslash\{\pm 1, \pm 2\}$ , with regular covering map $\pi: R \rightarrow U$ . Which subgroup of the full symmetric group of $\pi^{-1}(P)$ is obtained in this way from all such closed curves (with initial and final points $P)$ ?

Paper 3, Section II, G

Riemann Surfaces

Part II, 2010

Show that the analytic isomorphisms (i.e. conformal equivalences) of the Riemann sphere $\mathbb{C}_{\infty}$ to itself are given by the non-constant Möbius transformations.

State the Riemann-Hurwitz formula for a non-constant analytic map between compact Riemann surfaces, carefully explaining the terms which occur.

Suppose now that $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ is an analytic map of degree 2 ; show that there exist Möbius transformations $S$ and $T$ such that

S f T: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}

is the map given by $z \mapsto z^{2}$ .

Paper 1, Section I, J

Part II, 2010

Consider a binomial generalised linear model for data $y_{1}, \ldots, y_{n}$ modelled as realisations of independent $Y_{i} \sim \operatorname{Bin}\left(1, \mu_{i}\right)$ and logit $\operatorname{link} \mu_{i}=e^{\beta x_{i}} /\left(1+e^{\beta x_{i}}\right)$ for some known constants $x_{i}, i=1, \ldots, n$ , and unknown scalar parameter $\beta$ . Find the log-likelihood for $\beta$ , and the likelihood equation that must be solved to find the maximum likelihood estimator $\hat{\beta}$ of $\beta$ . Compute the second derivative of the log-likelihood for $\beta$ , and explain the algorithm you would use to find $\hat{\beta}$ .

Paper 2, Section I, J

Part II, 2010

Suppose you have a parametric model consisting of probability mass functions $f(y ; \theta), \theta \in \Theta \subset \mathbb{R}$ . Given a sample $Y_{1}, \ldots, Y_{n}$ from $f(y ; \theta)$ , define the maximum likelihood estimator $\hat{\theta}_{n}$ for $\theta$ and, assuming standard regularity conditions hold, state the asymptotic distribution of $\sqrt{n}\left(\hat{\theta}_{n}-\theta\right)$ .

Compute the Fisher information of a single observation in the case where $f(y ; \theta)$ is the probability mass function of a Poisson random variable with parameter $\theta$ . If $Y_{1}, \ldots, Y_{n}$ are independent and identically distributed random variables having a Poisson distribution with parameter $\theta$ , show that $\bar{Y}=\frac{1}{n} \sum_{i=1}^{n} Y_{i}$ and $S=\frac{1}{n-1} \sum_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}$ are unbiased estimators for $\theta$ . Without calculating the variance of $S$ , show that there is no reason to prefer $S$ over $\bar{Y}$ .

[You may use the fact that the asymptotic variance of $\sqrt{n}\left(\hat{\theta}_{n}-\theta\right)$ is a lower bound for the variance of any unbiased estimator.]

Paper 3, Section I, J

Part II, 2010

Consider the linear model $Y=X \beta+\varepsilon$ , where $Y$ is a $n \times 1$ random vector, $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$ , and where the $n \times p$ nonrandom matrix $X$ is known and has full column rank $p$ . Derive the maximum likelihood estimator $\hat{\sigma}^{2}$ of $\sigma^{2}$ . Without using Cochran's theorem, show carefully that $\hat{\sigma}^{2}$ is biased. Suggest another estimator $\tilde{\sigma}^{2}$ for $\sigma^{2}$ that is unbiased.

Paper 4, Section I, J

Part II, 2010

Below is a simplified 1993 dataset of US cars. The columns list index, make, model, price (in $\$ 1000)$ , miles per gallon, number of passengers, length and width in inches, and weight (in pounds). The data are displayed in $R$ as follows (abbreviated):

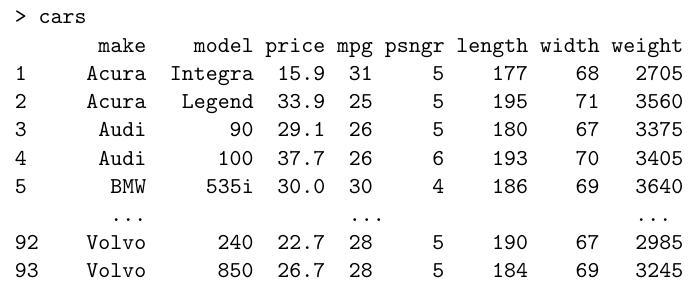
It is reasonable to assume that prices for different makes of car are independent. We model the logarithm of the price as a linear combination of the other quantitative properties of the cars and an error term. Write down this model mathematically. How would you instruct $R$ to fit this model and assign it to a variable "fit"?

$R$ provides the following (slightly abbreviated) summary:

Briefly explain the information that is being provided in each column of the table. What are your conclusions and how would you try to improve the model?

Paper 1, Section II, J

Part II, 2010

Consider a generalised linear model with parameter $\beta^{\top}$ partitioned as $\left(\beta_{0}^{\top}, \beta_{1}^{\top}\right)$ , where $\beta_{0}$ has $p_{0}$ components and $\beta_{1}$ has $p-p_{0}$ components, and consider testing $H_{0}: \beta_{1}=0$ against $H_{1}: \beta_{1} \neq 0$ . Define carefully the deviance, and use it to construct a test for $H_{0}$ .

[You may use Wilks' theorem to justify this test, and you may also assume that the dispersion parameter is known.]

Now consider the generalised linear model with Poisson responses and the canonical link function with linear predictor $\eta=\left(\eta_{1}, \ldots, \eta_{n}\right)^{T}$ given by $\eta_{i}=x_{i}^{\top} \beta, i=1, \ldots, n$ , where $x_{i 1}=1$ for every $i$ . Derive the deviance for this model, and argue that it may be approximated by Pearson's $\chi^{2}$ statistic.

Paper 4, Section II, J

Part II, 2010

Every day, Barney the darts player comes to our laboratory. We record his facial expression, which can be either "mad", "weird" or "relaxed", as well as how many units of beer he has drunk that day. Each day he tries a hundred times to hit the bull's-eye, and we write down how often he succeeds. The data look like this:

\begin{tabular}{rrrr} \multicolumn{1}{l}{} & & & \ Day & Beer & Expression & BullsEye \ 1 & 3 & Mad & 30 \ 2 & 3 & Mad & 32 \ $\vdots$ & $\vdots$ & $\vdots$ & $\vdots$ \ 60 & 2 & Mad & 37 \ 61 & 4 & Weird & 30 \ $\vdots$ & $\vdots$ & $\vdots$ & $\vdots$ \ 110 & 4 & Weird & 28 \ 111 & 2 & Relaxed & 35 \ $\vdots$ & $\vdots$ & $\vdots$ & $\vdots$ \ 150 & 3 & Relaxed & 31 \end{tabular}

Write down a reasonable model for $Y_{1}, \ldots, Y_{n}$ , where $n=150$ and where $Y_{i}$ is the number of times Barney has hit bull's-eye on the $i$ th day. Explain briefly why we may wish initially to include interactions between the variables. Write the $\mathrm{R}$ code to fit your model.

The scientist of the above story fitted her own generalized linear model, and subsequently obtained the following summary (abbreviated):

Why are ExpressionMad and Beer:ExpressionMad not listed? Suppose on a particular day, Barney's facial expression is weird, and he drank three units of beer. Give the linear predictor in the scientist's model for this day.

Based on the summary, how could you improve your model? How could one fit this new model in $R$ (without modifying the data file)?

Paper 2, Section II, C

Statistical Physics

Part II, 2010

Consider a 3-dimensional gas of $N$ non-interacting particles in a box of size $L$ where the allowed momenta are $\left\{\mathbf{p}_{i}\right\}$ . Assuming the particles have an energy $\epsilon(|\mathbf{p}|), \epsilon^{\prime}(p)>0$ , calculate the density of states $g(\epsilon) d \epsilon$ as $L \rightarrow \infty$ .

Treating the particles as classical explain why the partition function is

Z=\frac{z^{N}}{N !}, \quad z=\int_{0}^{\infty} d \epsilon g(\epsilon) e^{-\epsilon / k T}

Obtain an expression for the total energy $E$ .

Why is $\mathbf{p}_{i} \propto 1 / L ?$ By considering the dependence of the energies on the volume $V$ show that the pressure $P$ is given by

P V=\frac{N}{3 z} \int_{0}^{\infty} d \epsilon g(\epsilon) p \epsilon^{\prime}(p) e^{-\epsilon / k T}

What are the results for the pressure for non-relativistic particles and also for relativistic particles when their mass can be neglected?

What is the thermal wavelength for non-relativistic particles? Why are the classical results correct if the thermal wavelength is much smaller than the mean particle separation?

Paper 3, Section II, I

Part II, 2010

Cars looking for a parking space are directed to one of three unlimited parking lots A, B and C. First, immediately after the entrance, the road forks: one direction is to lot A, the other to B and C. Shortly afterwards, the latter forks again, between B and C. See the diagram below.

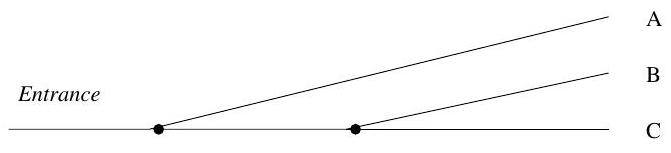
The policeman at the first road fork directs an entering car with probability $1 / 3$ to A and with probability $2 / 3$ to the second fork. The policeman at the second fork sends the passing cars to $\mathrm{B}$ or $\mathrm{C}$ alternately: cars $1,3,5, \ldots$ approaching the second fork go to $\mathrm{B}$ and cars $2,4,6, \ldots$ to $\mathrm{C}$ .

Assuming that the total arrival process $(N(t))$ of cars is Poisson of rate $\lambda$ , consider the processes $\left(X^{\mathrm{A}}(t)\right),\left(X^{\mathrm{B}}(t)\right)$ and $\left(X^{\mathrm{C}}(t)\right), t \geqslant 0$ , where $X^{i}(t)$ is the number of cars directed to lot $i$ by time $t$ , for $i=\mathrm{A}, \mathrm{B}, \mathrm{C}$ . The times for a car to travel from the first to the second fork, or from a fork to the parking lot, are all negligible.

(a) Characterise each of the processes $\left(X^{\mathrm{A}}(t)\right),\left(X^{\mathrm{B}}(t)\right)$ and $\left(X^{\mathrm{C}}(t)\right)$ , by specifying if it is (i) Poisson, (ii) renewal or (iii) delayed renewal. Correspondingly, specify the rate, the holding-time distribution and the distribution of the delay.

(b) In the case of a renewal process, determine the equilibrium delay distribution.

(c) Given $s, t>0$ , write down explicit expressions for the probability $\mathbb{P}\left(X^{i}(s)=X^{i}(s+t)\right)$ that the interval $(s, t+s)$ is free of points in the corresponding process, $i=\mathrm{A}, \mathrm{B}, \mathrm{C}$ .

Paper 3, Section II, C

Statistical Physics

Part II, 2010

(i) Given the following density of states for a particle in 3 dimensions

g(\varepsilon)=K V \varepsilon^{1 / 2}

write down the partition function for a gas of $N$ such non-interacting particles, assuming they can be treated classically. From this expression, calculate the energy $E$ of the system and the heat capacities $C_{V}$ and $C_{P}$ . You may take it as given that $P V=\frac{2}{3} E$ .

[Hint: The formula $\int_{0}^{\infty} d y y^{2} e^{-y^{2}}=\sqrt{\pi} / 4$ may be useful.]

(ii) Using thermodynamic relations obtain the relation between heat capacities and compressibilities

\frac{C_{P}}{C_{V}}=\frac{\kappa_{T}}{\kappa_{S}}

where the isothermal and adiabatic compressibilities are given by

\kappa=-\frac{1}{V} \frac{\partial V}{\partial P},

derivatives taken at constant temperature and entropy, respectively.

(iii) Find $\kappa_{T}$ and $\kappa_{S}$ for the ideal gas considered above.

Paper 4, Section II, C

Statistical Physics

Part II, 2010

(i) Let $\rho_{i}$ be the probability that a system is in a state labelled by $i$ with $N_{i}$ particles and energy $E_{i}$ . Define

s\left(\rho_{i}\right)=-k \sum_{i} \rho_{i} \log \rho_{i} .

$s\left(\rho_{i}\right)$ has a maximum, consistent with a fixed mean total number of particles $N$ , mean total energy $E$ and $\sum_{i} \rho_{i}=1$ , when $\rho_{i}=\bar{\rho}_{i}$ . Let $S(E, N)=s\left(\bar{\rho}_{i}\right)$ and show that

\frac{\partial S}{\partial E}=\frac{1}{T}, \quad \frac{\partial S}{\partial N}=-\frac{\mu}{T},

where $T$ may be identified with the temperature and $\mu$ with the chemical potential.

(ii) For two weakly coupled systems 1,2 then $\rho_{i, j}=\rho_{1, i} \rho_{2, j}$ and $E_{i, j}=E_{1, i}+E_{2, j}$ , $N_{i, j}=N_{1, i}+N_{2, j}$ . Show that $S(E, N)=S_{1}\left(E_{1}, N_{1}\right)+S_{2}\left(E_{2}, N_{2}\right)$ where, if $S(E, N)$ is stationary under variations in $E_{1}, E_{2}$ and $N_{1}, N_{2}$ for $E=E_{1}+E_{2}, N=N_{1}+N_{2}$ fixed, we must have $T_{1}=T_{2}, \mu_{1}=\mu_{2}$ .

(iii) Define the grand partition function $\mathcal{Z}(T, \mu)$ for the system in (i) and show that

k \log \mathcal{Z}=S-\frac{1}{T} E+\frac{\mu}{T} N, \quad S=\frac{\partial}{\partial T}(k T \log \mathcal{Z})

(iv) For a system with single particle energy levels $\epsilon_{r}$ the possible states are labelled by $i=\left\{n_{r}: n_{r}=0,1\right\}$ , where $N_{i}=\sum_{r} n_{r}, E_{i}=\sum_{r} n_{r} \epsilon_{r}$ and $\sum_{i}=\prod_{r} \sum_{n_{r}=0,1}$ . Show that

\bar{\rho}_{i}=\prod_{r} \frac{e^{-n_{r}\left(\epsilon_{r}-\mu\right) / k T}}{1+e^{-\left(\epsilon_{r}-\mu\right) / k T}} .

Calculate $\bar{n}_{r}$ . How is this related to a free fermion gas?

Paper 1, Section II, I

Part II, 2010

What is a Brownian motion? State the reflection principle for Brownian motion.

Let $W=\left(W_{t}\right)_{t \geqslant 0}$ be a Brownian motion. Let $M=\max _{0 \leqslant t \leqslant 1} W_{t}$ . Prove

\mathbb{P}\left(M \geqslant x, W_{1} \leqslant x-y\right)=\mathbb{P}\left(M \geqslant x, W_{1} \geqslant x+y\right)

for all $x, y \geqslant 0$ . Hence, show that the random variables $M$ and $\left|W_{1}\right|$ have the same distribution.

Find the density function of the random variable $R=W_{1} / M$ .

Paper 2, Section II, I

Part II, 2010

What is a martingale? What is a supermartingale? What is a stopping time?

Let $M=\left(M_{n}\right)_{n \geqslant 0}$ be a martingale and $\hat{M}=\left(\hat{M}_{n}\right)_{n \geqslant 0}$ a supermartingale with respect to a common filtration. If $M_{0}=\hat{M}_{0}$ , show that $\mathbb{E} M_{T} \geqslant \mathbb{E} \hat{M}_{T}$ for any bounded stopping time $T$ .

[If you use a general result about supermartingales, you must prove it.]

Consider a market with one stock with prices $S=\left(S_{n}\right)_{n \geqslant 0}$ and constant interest rate $r$ . Explain why an investor's wealth $X$ satisfies

X_{n}=(1+r) X_{n-1}+\pi_{n}\left[S_{n}-(1+r) S_{n-1}\right]

where $\pi_{n}$ is the number of shares of the stock held during the $n$ th period.

Given an initial wealth $X_{0}$ , an investor seeks to maximize $\mathbb{E} U\left(X_{N}\right)$ where $U$ is a given utility function. Suppose the stock price is such that $S_{n}=S_{n-1} \xi_{n}$ where $\left(\xi_{n}\right)_{n} \geqslant 1$ is a sequence of independent and identically distributed random variables. Let $V$ be defined inductively by

V(n, x, s)=\sup _{p \in \mathbb{R}} \mathbb{E} V\left[n+1,(1+r) x-p s\left(1+r-\xi_{1}\right), s \xi_{1}\right]

with terminal condition $V(N, x, s)=U(x)$ for all $x, s \in \mathbb{R}$ .

Show that the process $\left(V\left(n, X_{n}, S_{n}\right)\right)_{0 \leqslant n \leqslant N}$ is a supermartingale for any trading strategy $\pi$ .

Suppose $\pi^{*}$ is a trading strategy such that the corresponding wealth process $X^{*}$ makes $\left(V\left(n, X_{n}^{*}, S_{n}\right)\right)_{0} \leqslant n \leqslant N$ a martingale. Show that $\pi^{*}$ is optimal.

Paper 3, Section II, I

Part II, 2010

Consider a market with two assets, a riskless bond and a risky stock, both of whose initial (time-0) prices are $B_{0}=1=S_{0}$ . At time 1 , the price of the bond is a constant $B_{1}=R>0$ and the price of the stock $S_{1}$ is uniformly distributed on the interval $[0, C]$ where $C>R$ is a constant.

Describe the set of state price densities.

Consider a contingent claim whose payout at time 1 is given by $S_{1}^{2}$ . Use the fundamental theorem of asset pricing to show that, if there is no arbitrage, the initial price of the claim is larger than $R$ and smaller than $C$ .

Now consider an investor with initial wealth $X_{0}=1$ , and assume $C=3 R$ . The investor's goal is to maximize his expected utility of time-1 wealth $\mathbb{E} U\left[R+\pi\left(S_{1}-R\right)\right]$ , where $U(x)=\sqrt{x}$ . Show that the optimal number of shares of stock to hold is $\pi^{*}=1$ .

What would be the investor's marginal utility price of the contingent claim described above?

Paper 4, Section II, I

Part II, 2010

Consider a market with no riskless asset and $d$ risky stocks where the price of stock $i \in\{1, \ldots, d\}$ at time $t \in\{0,1\}$ is denoted $S_{t}^{i}$ . We assume the vector $S_{0} \in \mathbb{R}^{d}$ is not random, and we let $\mu=\mathbb{E} S_{1}$ and $V=\mathbb{E}\left[\left(S_{1}-\mu\right)\left(S_{1}-\mu\right)^{T}\right]$ . Assume $V$ is not singular.

Suppose an investor has initial wealth $X_{0}=x$ , which he invests in the $d$ stocks so that his wealth at time 1 is $X_{1}=\pi^{T} S_{1}$ for some $\pi \in \mathbb{R}^{d}$ . He seeks to minimize the $\operatorname{var}\left(X_{1}\right)$ subject to his budget constraint and the condition that $\mathbb{E} X_{1}=m$ for a given constant $m \in \mathbb{R}$ .

Illustrate this investor's problem by drawing a diagram of the mean-variance efficient frontier. Write down the Lagrangian for the problem. Show that there are two vectors $\pi_{A}$ and $\pi_{B}$ (which do not depend on the constants $x$ and $m$ ) such that the investor's optimal portfolio is a linear combination of $\pi_{A}$ and $\pi_{B}$ .

Another investor with initial wealth $Y_{0}=y$ seeks to maximize $\mathbb{E} U\left(Y_{1}\right)$ his expected utility of time 1 wealth, subject to his budget constraint. Assuming that $S_{1}$ is Gaussian and $U(w)=-e^{-\gamma w}$ for a constant $\gamma>0$ , show that the optimal portfolio in this case is also a linear combination of $\pi_{A}$ and $\pi_{B}$ .

[You may use the moment generating function of the Gaussian distribution without derivation.]

Continue to assume $S_{1}$ is Gaussian, but now assume that $U$ is increasing, concave, and twice differentiable, and that $U, U^{\prime}$ and $U^{\prime \prime}$ are of exponential growth but not necessarily of the form $U(w)=-e^{-\gamma w}$ . (Recall that a function $f$ is of exponential growth if $|f(w)| \leqslant a e^{b|w|}$ for some constants positive constants $a, b$ .) Prove that the utility maximizing investor still holds a linear combination of $\pi_{A}$ and $\pi_{B}$ .

[You may use the Gaussian integration by parts formula

\mathbb{E}[\nabla f(Z)]=\mathbb{E}[Z f(Z)]

where $Z=\left(Z_{1}, \ldots, Z_{d}\right)^{T}$ is a vector of independent standard normal random variables, and $f$ is differentiable and of exponential growth. You may also interchange integration and differentiation without justification.]

Paper 1, Section I, F

Part II, 2010

Let $(X, d)$ be a non-empty complete metric space with no isolated points, $G$ an open dense subset of $X$ and $E$ a countable dense subset of $X$ .

(i) Stating clearly any standard theorem you use, prove that $G \backslash E$ is a dense subset of $X$ .

(ii) If $G$ is only assumed to be uncountable and dense in $X$ , does it still follow that $G \backslash E$ is dense in $X$ ? Justify your answer.

Paper 2, Section I, F

Part II, 2010

(a) State the Weierstrass approximation theorem concerning continuous real functions on the closed interval $[0,1]$ .

(b) Let $f:[0,1] \rightarrow \mathbb{R}$ be continuous.

(i) If $\int_{0}^{1} f(x) x^{n} d x=0$ for each $n=0,1,2, \ldots$ , prove that $f$ is the zero function.

(ii) If we only assume that $\int_{0}^{1} f(x) x^{2 n} d x=0$ for each $n=0,1,2, \ldots$ , prove that it still follows that $f$ is the zero function.

[If you use the Stone-Weierstrass theorem, you must prove it.]

(iii) If we only assume that $\int_{0}^{1} f(x) x^{2 n+1} d x=0$ for each $n=0,1,2, \ldots$ , does it still follow that $f$ is the zero function? Justify your answer.

Paper 3, Section I, F

Part II, 2010

Let $A=\{z \in \mathbb{C}: 1 / 2 \leqslant|z| \leqslant 2\}$ and suppose that $f$ is complex analytic on an open subset containing $A$ .

(i) Give an example, with justification, to show that there need not exist a sequence of complex polynomials converging to $f$ uniformly on $A$ .

(ii) Let $R \subset \mathbb{C}$ be the positive real axis and $B=A \backslash R$ . Prove that there exists a sequence of complex polynomials $p_{1}, p_{2}, p_{3}, \ldots$ such that $p_{j} \rightarrow f$ uniformly on each compact subset of $B$ .

(iii) Let $p_{1}, p_{2}, p_{3}, \ldots$ be the sequence of polynomials in (ii). If this sequence converges uniformly on $A$ , show that $\int_{C} f(z) d z=0$ , where $C=\{z \in \mathbb{C}:|z|=1\}$ .

Paper 4, Section I, $2 F$

Part II, 2010

Find explicitly a polynomial $p$ of degree $\leqslant 3$ such that

\sup _{x \in[-1,1]}\left|x^{4}-p(x)\right| \leqslant \sup _{x \in[-1,1]}\left|x^{4}-q(x)\right|

for every polynomial $q$ of degree $\leqslant 3$ . Justify your answer.

Paper 4, Section II, I

Part II, 2010

(a) Let $\left(X_{t}\right)$ be an irreducible continuous-time Markov chain on a finite or countable state space. What does it mean to say that the chain is (i) transient, (ii) recurrent, (iii) positive recurrent, (iv) null recurrent? What is the relation between equilibrium distributions and properties (iii) and (iv)?

A population of microorganisms develops in continuous time; the size of the population is a Markov chain $\left(X_{t}\right)$ with states $0,1,2, \ldots$ Suppose $X_{t}=n$ . It is known that after a short time $s$ , the probability that $X_{t}$ increased by one is $\lambda(n+1) s+o(s)$ and (if $n \geqslant 1$ ) the probability that the population was exterminated between times $t$ and $t+s$ and never revived by time $t+s$ is $\mu s+o(s)$ . Here $\lambda$ and $\mu$ are given positive constants. All other changes in the value of $X_{t}$ have a combined probability $o(s)$ .

(b) Write down the Q-matrix of Markov chain $\left(X_{t}\right)$ and determine if $\left(X_{t}\right)$ is irreducible. Show that $\left(X_{t}\right)$ is non-explosive. Determine the jump chain.

(c) Now assume that

\mu=\lambda

Determine whether the chain is transient or recurrent, and in the latter case whether it is positive or null recurrent. Answer the same questions for the jump chain. Justify your answers.

Paper 2, Section II, 11F

Part II, 2010

Let

B_{r}(0)=\left\{(x, y) \in \mathbb{R}^{2}: x^{2}+y^{2}<r^{2}\right\},

$B=B_{1}(0)$ , and

C=\left\{(x, y) \in \mathbb{R}^{2}: x^{2}+y^{2}=1\right\}

Let $D=B \cup C$ .

(i) State the Brouwer fixed point theorem on the plane.

(ii) Show that the Brouwer fixed point theorem on the plane is equivalent to the nonexistence of a continuous map $F: D \rightarrow C$ such that $F(p)=p$ for each $p \in C$ .

(iii) Let $G: D \rightarrow \mathbb{R}^{2}$ be continuous, $0<\epsilon<1$ and suppose that

|p-G(p)|<\epsilon

for each $p \in C$ . Using the Brouwer fixed point theorem or otherwise, prove that

B_{1-\epsilon}(0) \subseteq G(B)

[Hint: argue by contradiction.]

(iv) Let $q \in B$ . Does there exist a continuous map $H: D \rightarrow \mathbb{R}^{2} \backslash\{q\}$ such that $H(p)=p$ for each $p \in C$ ? Justify your answer.

Paper 3, Section II, F

Part II, 2010

(i) Let $\gamma:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ be a continuous map with $\gamma(0)=\gamma(1)$ . Define the winding number $w(\gamma ; 0)$ of $\gamma$ about the origin.

(ii) For $j=0,1$ , let $\gamma_{j}:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ be continuous with $\gamma_{j}(0)=\gamma_{j}(1)$ . Make the following statement precise, and prove it: if $\gamma_{0}$ can be continuously deformed into $\gamma_{1}$ through a family of continuous curves missing the origin, then $w\left(\gamma_{0} ; 0\right)=w\left(\gamma_{1} ; 0\right)$ .

[You may use without proof the following fact: if $\gamma, \delta:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ are continuous with $\gamma(0)=\gamma(1), \delta(0)=\delta(1)$ and if $|\gamma(t)|<|\delta(t)|$ for each $t \in[0,1]$ , then $w(\gamma+\delta ; 0)=w(\delta ; 0)$ .]

(iii) Let $\gamma:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ be continuous with $\gamma(0)=\gamma(1)$ . If $\gamma(t)$ is not equal to a negative real number for each $t \in[0,1]$ , prove that $w(\gamma ; 0)=0$ .

(iv) Let $D=\{z \in \mathbb{C}:|z| \leqslant 1\}$ and $C=\{z \in \mathbb{C}:|z|=1\}$ . If $g: D \rightarrow C$ is continuous, prove that for each non-zero integer $n$ , there is at least one point $z \in C$ such that $z^{n}+g(z)=0$ .

Paper 1, Section II, A

Part II, 2010

Derive the wave equation governing the velocity potential $\phi$ for linearized sound waves in a compressible inviscid fluid. How is the pressure disturbance related to the velocity potential?

A semi-infinite straight tube of uniform cross-section is aligned along the positive $x$ -axis with its end at $x=-L$ . The tube is filled with fluid of density $\rho_{1}$ and sound speed $c_{1}$ in $-L<x<0$ and with fluid of density $\rho_{2}$ and sound speed $c_{2}$ in $x>0$ . A piston at the end of the tube performs small oscillations such that its position is $x=-L+\epsilon e^{i \omega t}$ , with $\epsilon \ll L$ and $\epsilon \omega \ll c_{1}, c_{2}$ . Show that the complex amplitude of the velocity potential in $x>0$ is

-\epsilon c_{1}\left(\frac{c_{1}}{c_{2}} \cos \frac{\omega L}{c_{1}}+i \frac{\rho_{2}}{\rho_{1}} \sin \frac{\omega L}{c_{1}}\right)^{-1} .

Calculate the time-averaged acoustic energy flux in $x>0$ . Comment briefly on the variation of this result with $L$ for the particular case $\rho_{2} \ll \rho_{1}$ and $c_{2}=\mathrm{O}\left(c_{1}\right)$ .

Paper 2, Section II, 38A

Part II, 2010

The equation of motion for small displacements $\mathbf{u}(\mathbf{x}, t)$ in a homogeneous, isotropic, elastic medium of density $\rho$ is

\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+\mu) \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{u})+\mu \nabla^{2} \mathbf{u}

where $\lambda$ and $\mu$ are the Lamé constants. Show that the dilatation $\nabla \cdot \mathbf{u}$ and rotation $\nabla \wedge \mathbf{u}$ each satisfy wave equations, and determine the corresponding wave speeds $c_{P}$ and $c_{S}$ .

Show also that a solution of the form $\mathbf{u}=\mathbf{A} \exp [i(\mathbf{k} \cdot \mathbf{x}-\omega t)]$ satisfies

\omega^{2} \mathbf{A}=c_{P}^{2} \mathbf{k}(\mathbf{k} \cdot \mathbf{A})-c_{S}^{2} \mathbf{k} \wedge(\mathbf{k} \wedge \mathbf{A})

Deduce the dispersion relation and the direction of polarization relative to $\mathbf{k}$ for plane harmonic $P$ -waves and plane harmonic $S$ -waves.

Now suppose the medium occupies the half-space $z \leqslant 0$ and that the boundary $z=0$ is stress free. Show that it is possible to find a self-sustained combination of evanescent $P$ -waves and $S V$ -waves (i.e. a Rayleigh wave), proportional to exp $[i k(x-c t)]$ and propagating along the boundary, provided the wavespeed $c$ satisfies

\left(2-\frac{c^{2}}{c_{S}^{2}}\right)^{2}=4\left(1-\frac{c^{2}}{c_{S}^{2}}\right)^{1 / 2}\left(1-\frac{c^{2}}{c_{P}^{2}}\right)^{1 / 2}

[You are not required to show that this equation has a solution.]

Paper 3, Section II, 38A

Part II, 2010

Consider the equation

\frac{\partial^{2} \phi}{\partial t \partial x}=-\alpha \phi

where $\alpha$ is a positive constant. Find the dispersion relation for waves of frequency $\omega$ and wavenumber $k$ . Sketch graphs of the phase velocity $c(k)$ and the group velocity $c_{g}(k)$ .

A disturbance localized near $x=0$ at $t=0$ evolves into a dispersing wave packet. Will the wavelength and frequency of the waves passing a stationary observer located at a large positive value of $x$ increase or decrease for $t>0$ ? In which direction do the crests pass the observer?

Write down the solution $\phi(x, t)$ with initial value

\phi(x, 0)=\int_{-\infty}^{\infty} A(k) e^{i k x} d k

What can be said about $A(-k)$ if $\phi$ is real?

Use the method of stationary phase to obtain an approximation for $\phi(V t, t)$ for fixed $V>0$ and large $t$ . What can be said about the solution at $x=-V t$ for large $t$ ?

[You may assume that $\int_{-\infty}^{\infty} e^{-a u^{2}} d u=\sqrt{\frac{\pi}{a}}$ for $\operatorname{Re}(a) \geqslant 0, a \neq 0$ .]

Paper 4, Section II, A

Part II, 2010

Starting from the equations for one-dimensional unsteady flow of an inviscid compressible fluid, show that it is possible to find Riemann invariants $u \pm Q$ that are constant on characteristics $C_{\pm}$ given by

\frac{d x}{d t}=u \pm c

where $u(x, t)$ is the velocity of the fluid and $c(x, t)$ is the local speed of sound. Show that $Q=2\left(c-c_{0}\right) /(\gamma-1)$ for the case of a perfect gas with adiabatic equation of state $p=p_{0}\left(\rho / \rho_{0}\right)^{\gamma}$ , where $p_{0}, \rho_{0}$ and $\gamma$ are constants, $\gamma>1$ and $c=c_{0}$ when $\rho=\rho_{0}$ .

Such a gas initially occupies the region $x>0$ to the right of a piston in an infinitely long tube. The gas is initially uniform and at rest with density $\rho_{0}$ . At $t=0$ the piston starts moving to the left at a constant speed $V$ . Assuming that the gas keeps up with the piston, find $u(x, t)$ and $c(x, t)$ in each of the three distinct regions that are defined by families of $C_{+}$ characteristics.

Now assume that the gas does not keep up with the piston. Show that the gas particle at $x=x_{0}$ when $t=0$ follows a trajectory given, for $t>x_{0} / c_{0}$ , by

x(t)=\frac{\gamma+1}{\gamma-1}\left(\frac{c_{0} t}{x_{0}}\right)^{2 /(\gamma+1)} x_{0}-\frac{2 c_{0} t}{\gamma-1}

Deduce that the velocity of any given particle tends to $-2 c_{0} /(\gamma-1)$ as $t \rightarrow \infty$ .

Paper 1, Section II, C

Asymptotic Methods

Part II, 2010

For $\lambda>0$ let

I(\lambda)=\int_{0}^{b} f(x) \mathrm{e}^{-\lambda x} d x, \quad \text { with } \quad 0<b<\infty

Assume that the function $f(x)$ is continuous on $0<x \leqslant b$ , and that

f(x) \sim x^{\alpha} \sum_{n=0}^{\infty} a_{n} x^{n \beta}

as $x \rightarrow 0_{+}$ , where $\alpha>-1$ and $\beta>0$ .

(a) Explain briefly why in this case straightforward partial integrations in general cannot be applied for determining the asymptotic behaviour of $I(\lambda)$ as $\lambda \rightarrow \infty$ .

(b) Derive with proof an asymptotic expansion for $I(\lambda)$ as $\lambda \rightarrow \infty$ .

(c) For the function

B(s, t)=\int_{0}^{1} u^{s-1}(1-u)^{t-1} d u, \quad s, t>0

obtain, using the substitution $u=e^{-x}$ , the first two terms in an asymptotic expansion as $s \rightarrow \infty$ . What happens as $t \rightarrow \infty$ ?

[Hint: The following formula may be useful

\Gamma(y)=\int_{0}^{\infty} x^{y-1} \mathrm{e}^{-x} d t, \quad \text { for } \quad x>0

Paper 3, Section II, C

Asymptotic Methods

Part II, 2010

Consider the ordinary differential equation

y^{\prime \prime}=(|x|-E) y

subject to the boundary conditions $y(\pm \infty)=0$ . Write down the general form of the Liouville-Green solutions for this problem for $E>0$ and show that asymptotically the eigenvalues $E_{n}, n \in \mathbb{N}$ and $E_{n}<E_{n+1}$ , behave as $E_{n}=\mathrm{O}\left(n^{2 / 3}\right)$ for large $n$ .

Paper 4, Section II, C

Asymptotic Methods

Part II, 2010

(a) Consider for $\lambda>0$ the Laplace type integral

I(\lambda)=\int_{a}^{b} f(t) \mathrm{e}^{-\lambda \phi(t)} d t

for some finite $a, b \in \mathbb{R}$ and smooth, real-valued functions $f(t), \phi(t)$ . Assume that the function $\phi(t)$ has a single minimum at $t=c$ with $a<c<b$ . Give an account of Laplace's method for finding the leading order asymptotic behaviour of $I(\lambda)$ as $\lambda \rightarrow \infty$ and briefly discuss the difference if instead $c=a$ or $c=b$ , i.e. when the minimum is attained at the boundary.

(b) Determine the leading order asymptotic behaviour of

I(\lambda)=\int_{-2}^{1} \cos t \mathrm{e}^{-\lambda t^{2}} d t

as $\lambda \rightarrow \infty$

(c) Determine also the leading order asymptotic behaviour when cos $t$ is replaced by $\sin t$ in $(*)$ .

Paper 1, Section I, D

Part II, 2010

A system with coordinates $q_{i}, i=1, \ldots, n$ , has the Lagrangian $L\left(q_{i}, \dot{q}_{i}\right)$ . Define the energy $E$ .

Consider a charged particle, of mass $m$ and charge $e$ , moving with velocity $\mathbf{v}$ in the presence of a magnetic field $\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}$ . The usual vector equation of motion can be derived from the Lagrangian

L=\frac{1}{2} m \mathbf{v}^{2}+e \mathbf{v} \cdot \mathbf{A}

where $\mathbf{A}$ is the vector potential.

The particle moves in the presence of a field such that

\mathbf{A}=(0, r g(z), 0), \quad g(z)>0

referred to cylindrical polar coordinates $(r, \phi, z)$ . Obtain two constants of the motion, and write down the Lagrangian equations of motion obtained by variation of $r, \phi$ and $z$ .

Show that, if the particle is projected from the point $\left(r_{0}, \phi_{0}, z_{0}\right)$ with velocity $\left(0,-2(e / m) r_{0} g\left(z_{0}\right), 0\right)$ , it will describe a circular orbit provided that $g^{\prime}\left(z_{0}\right)=0$ .

Paper 3, Section II, G

Algebraic Geometry

Part II, 2010

(i) Let $X$ be a curve, and $p \in X$ be a smooth point on $X$ . Define what a local parameter at $p$ is.

Now let $f: X \rightarrow Y$ be a rational map to a quasi-projective variety $Y$ . Show that if $Y$ is projective, $f$ extends to a morphism defined at $p$ .

Give an example where this fails if $Y$ is not projective, and an example of a morphism $f: \mathbb{C}^{2} \backslash\{0\} \rightarrow \mathbf{P}^{1}$ which does not extend to $0 .$

(ii) Let $V=Z\left(X_{0}^{8}+X_{1}^{8}+X_{2}^{8}\right)$ and $W=Z\left(X_{0}^{4}+X_{1}^{4}+X_{2}^{4}\right)$ be curves in $\mathbf{P}^{2}$ over a field of characteristic not equal to 2 . Let $\phi: V \rightarrow W$ be the map $\left[X_{0}: X_{1}: X_{2}\right] \mapsto\left[X_{0}^{2}: X_{1}^{2}: X_{2}^{2}\right]$ . Determine the degree of $\phi$ , and the ramification $e_{p}$ for all $p \in V$ .

Paper 2, Section I, D

Part II, 2010

Given the form

T=\frac{1}{2} T_{i j} \dot{q}_{i} \dot{q}_{j}, \quad V=\frac{1}{2} V_{i j} q_{i} q_{j}

for the kinetic energy $T$ and potential energy $V$ of a mechanical system, deduce Lagrange's equations of motion.

A light elastic string of length $4 b$ , fixed at both ends, has three particles, each of mass $m$ , attached at distances $b, 2 b, 3 b$ from one end. Gravity can be neglected. The particles vibrate with small oscillations transversely to the string, the tension $S$ in the string providing the restoring force. Take the displacements of the particles, $q_{i}, i=1,2,3$ , to be the generalized coordinates. Take units such that $m=1, S / b=1$ and show that

V=\frac{1}{2}\left[q_{1}^{2}+\left(q_{1}-q_{2}\right)^{2}+\left(q_{2}-q_{3}\right)^{2}+{q_{3}}^{2}\right]

Find the normal-mode frequencies for this system.

Paper 3, Section I, D

Part II, 2010

Euler's equations for the angular velocity $\boldsymbol{\omega}=\left(\omega_{1}, \omega_{2}, \omega_{3}\right)$ of a rigid body, viewed in the body frame, are

I_{1} \frac{d \omega_{1}}{d t}=\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3}

and cyclic permutations, where the principal moments of inertia are assumed to obey $I_{1}<I_{2}<I_{3}$ .

Write down two quadratic first integrals of the motion.

There is a family of solutions $\boldsymbol{\omega}(t)$ , unique up to time-translations $t \rightarrow\left(t-t_{0}\right)$ , which obey the boundary conditions $\boldsymbol{\omega} \rightarrow(0, \Omega, 0)$ as $t \rightarrow-\infty$ and $\boldsymbol{\omega} \rightarrow(0,-\Omega, 0)$ as $t \rightarrow \infty$ , for a given positive constant $\Omega$ . Show that, for such a solution, one has

\mathbf{L}^{2}=2 E I_{2},

where $\mathbf{L}$ is the angular momentum and $E$ is the kinetic energy.

By eliminating $\omega_{1}$ and $\omega_{3}$ in favour of $\omega_{2}$ , or otherwise, show that, in this case, the second Euler equation reduces to

\frac{d s}{d \tau}=1-s^{2}

where $s=\omega_{2} / \Omega$ and $\tau=\Omega t\left[\left(I_{1}-I_{2}\right)\left(I_{2}-I_{3}\right) / I_{1} I_{3}\right]^{1 / 2}$ . Find the general solution $s(\tau)$ .

[You are not expected to calculate $\omega_{1}(t)$ or $\left.\omega_{3}(t) .\right]$

Paper 4, Section I, D

Part II, 2010

A system with one degree of freedom has Lagrangian $L(q, \dot{q})$ . Define the canonical momentum $p$ and the energy $E$ . Show that $E$ is constant along any classical path.

Consider a classical path $q_{c}(t)$ with the boundary-value data

q_{c}(0)=q_{I}, \quad q_{c}(T)=q_{F}, \quad T>0

Define the action $S_{c}\left(q_{I}, q_{F}, T\right)$ of the path. Show that the total derivative $d S_{c} / d T$ along the classical path obeys

\frac{d S_{c}}{d T}=L

Using Lagrange's equations, or otherwise, deduce that

\frac{\partial S_{c}}{\partial q_{F}}=p_{F}, \quad \frac{\partial S_{c}}{\partial T}=-E,

where $p_{F}$ is the final momentum.

Paper 2, Section II, D

Part II, 2010

An axially-symmetric top of mass $m$ is free to rotate about a fixed point $O$ on its axis. The principal moments of inertia about $O$ are $A, A, C$ , and the centre of gravity $G$ is at a distance $\ell$ from $O$ . Define Euler angles $\theta, \phi$ and $\psi$ which specify the orientation of the top, where $\theta$ is the inclination of $O G$ to the upward vertical. Show that there are three conserved quantities for the motion, and give their physical meaning.

Initially, the top is spinning with angular velocity $n$ about $O G$ , with $G$ vertically above $O$ , before being disturbed slightly. Show that, in the subsequent motion, $\theta$ will remain close to zero provided $C^{2} n^{2}>4 m g \ell A$ , but that if $C^{2} n^{2}<4 m g \ell A$ , then $\theta$ will attain a maximum value given by

\cos \theta \simeq\left(C^{2} n^{2} / 2 m g \ell A\right)-1

Paper 4, Section II, D

Part II, 2010

A system is described by the Hamiltonian $H(q, p)$ . Define the Poisson bracket $\{f, g\}$ of two functions $f(q, p, t), g(q, p, t)$ , and show from Hamilton's equations that

\frac{d f}{d t}=\{f, H\}+\frac{\partial f}{\partial t}

Consider the Hamiltonian

H=\frac{1}{2}\left(p^{2}+\omega^{2} q^{2}\right)

and define

a=(p-i \omega q) /(2 \omega)^{1 / 2}, \quad a^{*}=(p+i \omega q) /(2 \omega)^{1 / 2},

where $i=\sqrt{-1}$ . Evaluate $\{a, a\}$ and $\left\{a, a^{*}\right\}$ , and show that $\{a, H\}=-i \omega a$ and $\left\{a^{*}, H\right\}=i \omega a^{*}$ . Show further that, when $f(q, p, t)$ is regarded as a function of the independent complex variables $a, a^{*}$ and of $t$ , one has

\frac{d f}{d t}=i \omega\left(a^{*} \frac{\partial f}{\partial a^{*}}-a \frac{\partial f}{\partial a}\right)+\frac{\partial f}{\partial t}

Deduce that both $\log a^{*}-i \omega t$ and $\log a+i \omega t$ are constant during the motion.

Paper 1, Section I, H

Part II, 2010

Explain what is meant by saying that a binary code $\mathcal{C}$ is a decodable code with words $C_{j}$ of length $l_{j}$ for $1 \leqslant j \leqslant n$ . Prove the MacMillan inequality which states that, for such a code,

\sum_{j=1}^{n} 2^{-l_{j}} \leqslant 1

Paper 2, Section I, $4 \mathrm{H}$

Part II, 2010

Describe the standard Hamming code of length 7 , proving that it corrects a single error. Find its weight enumeration polynomial.

Paper 3, Section I, $4 \mathrm{H}$

Part II, 2010

What is a linear code? What is a parity check matrix for a linear code? What is the minimum distance $d(C)$ for a linear code $C ?$

If $C_{1}$ and $C_{2}$ are linear codes having a certain relation (which you should specify), define the bar product $C_{1} \mid C_{2}$ . Show that

d\left(C_{1} \mid C_{2}\right)=\min \left\{2 d\left(C_{1}\right), d\left(C_{2}\right)\right\}

If $C_{1}$ has parity check matrix $P_{1}$ and $C_{2}$ has parity check matrix $P_{2}$ , find a parity check matrix for $C_{1} \mid C_{2}$ .

Paper 4, Section I, H

Part II, 2010

What is the discrete logarithm problem?

Describe the Diffie-Hellman key exchange system for two people. What is the connection with the discrete logarithm problem? Why might one use this scheme rather than just a public key system or a classical (pre-1960) coding system?

Extend the Diffie-Hellman system to $n$ people using $n(n-1)$ transmitted numbers.

Paper 1, Section II, H

Part II, 2010

State and prove Shannon's theorem for the capacity of a noisy memoryless binary symmetric channel, defining the terms you use.

[You may make use of any form of Stirling's formula and any standard theorems from probability, provided that you state them exactly.]

Paper 4, Section II, G

Algebraic Geometry

Part II, 2010

Let $E \subseteq \mathbf{P}^{2}$ be the projective curve obtained from the affine curve $y^{2}=\left(x-\lambda_{1}\right)\left(x-\lambda_{2}\right)\left(x-\lambda_{3}\right)$ , where the $\lambda_{i}$ are distinct and $\lambda_{1} \lambda_{2} \lambda_{3} \neq 0$ .

(i) Show there is a unique point at infinity, $P_{\infty}$ .

(ii) Compute $\operatorname{div}(x), \operatorname{div}(y)$ .

(iii) Show $\mathcal{L}\left(P_{\infty}\right)=k$ .

(iv) Compute $l\left(n P_{\infty}\right)$ for all $n$ .

[You may not use the Riemann-Roch theorem.]

Paper 2, Section II, H

Part II, 2010

The Van der Monde matrix $V\left(x_{0}, x_{1}, \ldots, x_{r-1}\right)$ is the $r \times r$ matrix with $(i, j)$ th entry $x_{i-1}^{j-1}$ . Find an expression for $\operatorname{det} V\left(x_{0}, x_{1}, \ldots, x_{r-1}\right)$ as a product. Explain why this expression holds if we work modulo $p$ a prime.

Show that $\operatorname{det} V\left(x_{0}, x_{1}, \ldots, x_{r-1}\right) \equiv 0$ modulo $p$ if $r>p$ , and that there exist $x_{0}, \ldots, x_{p-1}$ such that $\operatorname{det} V\left(x_{0}, x_{1}, \ldots, x_{p-1}\right) \not \equiv 0$ . By using Wilson's theorem, or otherwise, find the possible values of $\operatorname{det} V\left(x_{0}, x_{1}, \ldots, x_{p-1}\right)$ modulo $p$ .

The Dark Lord Y'Trinti has acquired the services of the dwarf Trigon who can engrave pairs of very large integers on very small rings. The Dark Lord wishes Trigon to engrave $n$ rings in such a way that anyone who acquires $r$ of the rings and knows the Prime Perilous $p$ can deduce the Integer $N$ of Power, but owning $r-1$ rings will give no information whatsoever. The integers $N$ and $p$ are very large and $p>N$ . Advise the Dark Lord.

For reasons to be explained in the prequel, Trigon engraves an $(n+1)$ st ring with random integers. A band of heroes (who know the Prime Perilous and all the information contained in this question) set out to recover the rings. What, if anything, can they say, with very high probability, about the Integer of Power if they have $r$ rings (possibly including the fake)? What can they say if they have $r+1$ rings? What if they have $r+2$ rings?

Paper 1, Section I, D

Part II, 2010

What is meant by the expression 'Hubble time'?

For $a(t)$ the scale factor of the universe and assuming $a(0)=0$ and $a\left(t_{0}\right)=1$ , where $t_{0}$ is the time now, obtain a formula for the size of the particle horizon $R_{0}$ of the universe.

Taking

a(t)=\left(t / t_{0}\right)^{\alpha},

show that $R_{0}$ is finite for certain values of $\alpha$ . What might be the physically relevant values of $\alpha$ ? Show that the age of the universe is less than the Hubble time for these values of $\alpha$ .

Paper 2, Section I, D

Part II, 2010

The number density $n=N / V$ for a photon gas in equilibrium is given by

n=\frac{8 \pi}{c^{3}} \int_{0}^{\infty} \frac{\nu^{2}}{e^{h \nu / k T}-1} d \nu

where $\nu$ is the photon frequency. By letting $x=h \nu / k T$ , show that

n=\alpha T^{3}

where $\alpha$ is a constant which need not be evaluated.

The photon entropy density is given by

s=\beta T^{3}

where $\beta$ is a constant. By considering the entropy, explain why a photon gas cools as the universe expands.

Paper 3, Section I, D

Part II, 2010

Consider a homogenous and isotropic universe with mass density $\rho(t)$ , pressure $P(t)$ and scale factor $a(t)$ . As the universe expands its energy changes according to the relation $d E=-P d V$ . Use this to derive the fluid equation

\dot{\rho}=-3 \frac{\dot{a}}{a}\left(\rho+\frac{P}{c^{2}}\right)

Use conservation of energy applied to a test particle at the boundary of a spherical fluid element to derive the Friedmann equation

\left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi}{3} G \rho-\frac{k}{a^{2}} c^{2}

where $k$ is a constant. State any assumption you have made. Briefly state the significance of $k$ .

Paper 4, Section I, D

Part II, 2010

The linearised equation for the growth of density perturbations, $\delta_{\mathbf{k}}$ , in an isotropic and homogenous universe is

\ddot{\delta}_{\mathbf{k}}+2 \frac{\dot{a}}{a} \dot{\delta}_{\mathbf{k}}+\left(\frac{c_{s}^{2} \mathbf{k}^{2}}{a^{2}}-4 \pi G \rho\right) \delta_{\mathbf{k}}=0

where $\rho$ is the density of matter, $c_{s}$ the sound speed, $c_{s}^{2}=d P / d \rho$ , and $\mathbf{k}$ is the comoving wavevector and $a(t)$ is the scale factor of the universe.

What is the Jean's length? Discuss its significance for the growth of perturbations.

Consider a universe filled with pressure-free matter with $a(t)=\left(t / t_{0}\right)^{2 / 3}$ . Compute the resulting equation for the growth of density perturbations. Show that your equation has growing and decaying modes and comment briefly on the significance of this fact.

Paper 1, Section II, D

Part II, 2010

A star has pressure $P(r)$ and mass density $\rho(r)$ , where $r$ is the distance from the centre of the star. These quantities are related by the pressure support equation

P^{\prime}=-\frac{G m \rho}{r^{2}}

where $P^{\prime}=d P / d r$ and $m(r)$ is the mass within radius $r$ . Use this to derive the virial theorem

E_{\text {grav }}=-3\langle P\rangle V,

where $E_{\text {grav }}$ is the total gravitational potential energy and $\langle P\rangle$ the average pressure.

The total kinetic energy of a spherically symmetric star is related to $\langle P\rangle$ by

E_{\mathrm{kin}}=\alpha\langle P\rangle V

where $\alpha$ is a constant. Use the virial theorem to determine the condition on $\alpha$ for gravitational binding. By considering the relation between pressure and 'internal energy' $U$ for an ideal gas, determine $\alpha$ for the cases of a) an ideal gas of non-relativistic particles, b) an ideal gas of ultra-relativistic particles.

Why does your result imply a maximum mass for any star? Briefly explain what is meant by the Chandrasekhar limit.

A white dwarf is in orbit with a companion star. It slowly accretes matter from the other star until its mass exceeds the Chandrasekhar limit. Briefly explain its subsequent evolution.

Paper 3, Section II, D

Part II, 2010

The number density for particles in thermal equilibrium, neglecting quantum effects, is

n=g_{s} \frac{4 \pi}{h^{3}} \int p^{2} d p \exp (-(E(p)-\mu) / k T)

where $g_{s}$ is the number of degrees of freedom for the particle with energy $E(p)$ and $\mu$ is its chemical potential. Evaluate $n$ for a non-relativistic particle.

Thermal equilibrium between two species of non-relativistic particles is maintained by the reaction

a+\alpha \leftrightarrow b+\beta

where $\alpha$ and $\beta$ are massless particles. Evaluate the ratio of number densities $n_{a} / n_{b}$ given that their respective masses are $m_{a}$ and $m_{b}$ and chemical potentials are $\mu_{a}$ and $\mu_{b}$ .

Explain how a reaction like the one above is relevant to the determination of the neutron to proton ratio in the early universe. Why does this ratio not fall rapidly to zero as the universe cools?

Explain briefly the process of primordial nucleosynthesis by which neutrons are converted into stable helium nuclei. Letting

Y_{H e}=\rho_{H e} / \rho

be the fraction of the universe's helium, compute $Y_{H e}$ as a function of the ratio $r=n_{n} / n_{p}$ at the time of nucleosynthesis.

Paper 1, Section II, H

Part II, 2010

(i) State the definition of smooth manifold with boundary and define the notion of boundary. Show that the boundary $\partial X$ is a manifold (without boundary) with $\operatorname{dim} \partial X=\operatorname{dim} X-1$ .

(ii) Let $0<a<1$ and let $x_{1}, x_{2}, x_{3}, x_{4}$ denote Euclidean coordinates on $\mathbb{R}^{4}$ . Show that the set

$X=\left\{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}-x_{4}^{2} \leqslant a\right\} \cap\left\{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}=1\right\} \cap\left\{x_{1}^{2}+2 x_{2}^{2}+x_{3}^{2}+x_{4}^{2}=3 / 2\right\}$

is a manifold with boundary and compute its dimension. You may appeal to standard results concerning regular values of smooth functions.

(iii) Determine if the following statements are true or false, giving reasons:

a. If $X$ and $Y$ are manifolds, $f: X \rightarrow Y$ smooth and $Z \subset Y$ a submanifold of codimension $r$ such that $f$ is not transversal to $Z$ , then $f^{-1}(Z)$ is not a submanifold of codimension $r$ in $X$ .

b. If $X$ and $Y$ are manifolds and $f: X \rightarrow Y$ is smooth, then the set of regular values of $f$ is open in $Y$ .

c. If $X$ and $Y$ are manifolds and $f: X \rightarrow Y$ is smooth then the set of critical points is of measure 0 in $X$ .

Paper 2, Section II, H

Part II, 2010

(i) State and prove the isoperimetric inequality for plane curves. You may appeal to Wirtinger's inequality as long as you state it precisely.

(ii) State Fenchel's theorem for curves in space.

(iii) Let $\alpha: I \rightarrow \mathbb{R}^{2}$ be a closed regular plane curve bounding a region $K$ . Suppose $K \supset\left[p_{1}, p_{1}+d_{1}\right] \times\left[p_{2}, p_{2}+d_{2}\right]$ , for $d_{1}>0, d_{2}>0$ , i.e. $K$ contains a rectangle of dimensions $d_{1}, d_{2}$ . Let $k(s)$ denote the signed curvature of $\alpha$ with respect to the inward pointing normal, where $\alpha$ is parametrised anticlockwise. Show that there exists an $s_{0} \in I$ such that $k\left(s_{0}\right) \leqslant \sqrt{\pi /\left(d_{1} d_{2}\right)}$ .

Paper 3, Section II, H

Part II, 2010

(i) State and prove the Theorema Egregium.

(ii) Define the notions principal curvatures, principal directions and umbilical point.

(iii) Let $S \subset \mathbb{R}^{3}$ be a connected compact regular surface (without boundary), and let $D \subset S$ be a dense subset of $S$ with the following property. For all $p \in D$ , there exists an open neighbourhood $\mathcal{U}_{p}$ of $p$ in $S$ such that for all $\theta \in[0,2 \pi), \psi_{p, \theta}\left(\mathcal{U}_{p}\right)=\mathcal{U}_{p}$ , where $\psi_{p, \theta}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$ denotes rotation by $\theta$ around the line through $p$ perpendicular to $T_{p} S$ . Show that $S$ is in fact a sphere.

Paper 1, Section II, H

Part II, 2010

State the path lifting and homotopy lifting lemmas for covering maps. Suppose that $X$ is path connected and locally path connected, that $p_{1}: Y_{1} \rightarrow X$ and $p_{2}: Y_{2} \rightarrow X$ are covering maps, and that $Y_{1}$ and $Y_{2}$ are simply connected. Using the lemmas you have stated, but without assuming the correspondence between covering spaces and subgroups of $\pi_{1}$ , prove that $Y_{1}$ is homeomorphic to $Y_{2}$ .

Paper 4, Section II, H

Part II, 2010

(i) Let $S \subset \mathbb{R}^{3}$ be a regular surface. Define the notions exponential map, geodesic polar coordinates, geodesic circles.

(ii) State and prove Gauss' lemma.

(iii) Let $S$ be a regular surface. For fixed $r>0$ , and points $p, q$ in $S$ , let $S_{r}(p)$ , $S_{r}(q)$ denote the geodesic circles around $p, q$ , respectively, of radius $r$ . Show the following statement: for each $p \in S$ , there exists an $r=r(p)>0$ and a neighborhood $\mathcal{U}_{p}$ containing $p$ such that for all $q \in \mathcal{U}_{p}$ , the sets $S_{r}(p)$ and $S_{r}(q)$ are smooth 1-dimensional manifolds which intersect transversally. What is the cardinality $\bmod 2$ of $S_{r}(p) \cap S_{r}(q)$ ?

Paper 1, Section I, D

Part II, 2010

Consider the 2-dimensional flow

\dot{x}=-\mu x+y, \quad \dot{y}=\frac{x^{2}}{1+x^{2}}-\nu y

where $x(t)$ and $y(t)$ are non-negative, the parameters $\mu$ and $\nu$ are strictly positive and $\mu \neq \nu$ . Sketch the nullclines in the $x, y$ plane. Deduce that for $\mu<\mu_{c}$ (where $\mu_{c}$ is to be determined) there are three fixed points. Find them and determine their type.

Sketch the phase portrait for $\mu<\mu_{c}$ and identify, qualitatively on your sketch, the stable and unstable manifolds of the saddle point. What is the final outcome of this system?

Paper 2, Section I, D

Part II, 2010

Consider the 2-dimensional flow

\dot{x}=\mu\left(\frac{1}{3} x^{3}-x\right)+y, \quad \dot{y}=-x

where the parameter $\mu>0$ . Using Lyapunov's approach, discuss the stability of the fixed point and its domain of attraction. Relevant definitions or theorems that you use should be stated carefully, but proofs are not required.

Paper 3, Section I, D

Part II, 2010

Let $I=[0,1)$ . The sawtooth (Bernoulli shift) map $F: I \rightarrow I$ is defined by

F(x)=2 x[\bmod 1]

Describe the effect of $F$ using binary notation. Show that $F$ is continuous on $I$ except at $x=\frac{1}{2}$ . Show also that $F$ has $N$ -periodic points for all $N \geqslant 2$ . Are they stable?

Explain why $F$ is chaotic, using Glendinning's definition.

Paper 4, Section I, D

Part II, 2010

Consider the 2-dimensional flow

\dot{x}=y+\frac{1}{4} x\left(1-2 x^{2}-2 y^{2}\right), \quad \dot{y}=-x+\frac{1}{2} y\left(1-x^{2}-y^{2}\right)

Use the Poincaré-Bendixson theorem, which should be stated carefully, to obtain a domain $\mathcal{D}$ in the $x y$ -plane, within which there is at least one periodic orbit.

Paper 3, Section II, D

Part II, 2010

Describe informally the concepts of extended stable manifold theory. Illustrate your discussion by considering the 2-dimensional flow

\dot{x}=\mu x+x y-x^{3}, \quad \dot{y}=-y+y^{2}-x^{2},

where $\mu$ is a parameter with $|\mu| \ll 1$ , in a neighbourhood of the origin. Determine the nature of the bifurcation.

Paper 4, Section II, D

Part II, 2010

Let $I=[0,1]$ and consider continuous maps $F: I \rightarrow I$ . Give an informal outline description of the two different bifurcations of fixed points of $F$ that can occur.

Illustrate your discussion by considering in detail the logistic map

F(x)=\mu x(1-x),

for $\mu \in(0,1+\sqrt{6}]$ .

Describe qualitatively what happens for $\mu \in(1+\sqrt{6}, 4]$ .

[You may assume without proof that

x-F^{2}(x)=x(\mu x-\mu+1)\left(\mu^{2} x^{2}-\mu(\mu+1) x+\mu+1\right)

Paper 1, Section II, B

Electrodynamics

Part II, 2010

The vector potential $A^{\mu}$ is determined by a current density distribution $j^{\mu}$ in the gauge $\partial_{\mu} A^{\mu}=0$ by

\square A^{\mu}=-\mu_{0} j^{\mu}, \quad \square=-\frac{\partial^{2}}{\partial t^{2}}+\nabla^{2},

in units where $c=1$ .

Describe how to justify the result

A^{\mu}(\mathbf{x}, t)=\frac{\mu_{0}}{4 \pi} \int d^{3} x^{\prime} \frac{j^{\mu}\left(\mathbf{x}^{\prime}, t^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|}, \quad t^{\prime}=t-\left|\mathbf{x}-\mathbf{x}^{\prime}\right|

A plane square loop of thin wire, edge lengths $l$ , has its centre at the origin and lies in the $(x, y)$ plane. For $t<0$ , no current is flowing in the loop, but at $t=0$ a constant current $I$ is turned on.

Find the vector potential at the point $(0,0, z)$ as a function of time due to a single edge of the loop.

What is the electric field due to the entire loop at $(0,0, z)$ as a function of time? Give a careful justification of your answer.

Paper 3, Section II, B

Electrodynamics

Part II, 2010

A particle of rest-mass $m$ , electric charge $q$ , is moving relativistically along the path $x^{\mu}(s)$ where $s$ parametrises the path.

Write down an action for which the extremum determines the particle's equation of motion in an electromagnetic field given by the potential $A^{\mu}(x)$ .

Use your action to derive the particle's equation of motion in a form where $s$ is the proper time.

Suppose that the electric and magnetic fields are given by

\begin{aligned} \mathbf{E} &=(0,0, E) \\ \mathbf{B} &=(0, B, 0) \end{aligned}

where $E$ and $B$ are constants and $B>E>0$ .

Find $x^{\mu}(s)$ given that the particle starts at rest at the origin when $s=0$ .

Describe qualitatively the motion of the particle.

Paper 4, Section II, B

Electrodynamics

Part II, 2010

In a superconductor the number density of charge carriers of charge $q$ is $n_{s}$ . Suppose that there is a time-independent magnetic field described by the three-vector potential $\mathbf{A} .$

Derive an expression for the superconducting current.

Explain how your answer is gauge invariant.

Suppose that for $z<0$ there is a constant magnetic field $\mathbf{B}_{0}$ in a vacuum and, for $z>0$ , there is a uniform superconductor. Derive the magnetic field for $z>0$ .

Paper 2, Section II, $\mathbf{2 1 H}$

Part II, 2010

Let $G$ be the finitely presented group $G=\left\langle a, b \mid a^{2} b^{3} a^{3} b^{2}=1\right\rangle$ . Construct a path connected space $X$ with $\pi_{1}(X, x) \cong G$ . Show that $X$ has a unique connected double cover $\pi: Y \rightarrow X$ , and give a presentation for $\pi_{1}(Y, y)$ .

Paper 1, Section II, A

Part II, 2010

Write down the Navier-Stokes equation for the velocity $\mathbf{u}(\mathbf{x}, t)$ of an incompressible viscous fluid of density $\rho$ and kinematic viscosity $\nu$ . Cast the equation into dimensionless form. Define rectilinear flow, and explain why the spatial form of any steady rectilinear flow is independent of the Reynolds number.

(i) Such a fluid is contained between two infinitely long plates at $y=0, y=a$ . The lower plate is at rest while the upper plate moves at constant speed $U$ in the $x$ direction. There is an applied pressure gradient $d p / d x=-G \rho \nu$ in the $x$ direction. Determine the flow field.

(ii) Now there is no applied pressure gradient, but baffles are attached to the lower plate at a distance $L$ from each other $(L \gg a)$ , lying between the plates so as to prevent any net volume flux in the $x$ direction. Assuming that far from the baffles the flow is essentially rectilinear, determine the flow field and the pressure gradient in the fluid.

Paper 2, Section II, A

Part II, 2010

What is lubrication theory? Explain the assumptions that go into the theory.

Viscous fluid with dynamic viscosity $\mu$ and density $\rho$ is contained between two flat plates, which approach each other at uniform speed $V$ . The first is fixed at $y=0,-L<x<L$ . The second has its ends at $\left(-L, h_{0}-\Delta h-V t\right),\left(L, h_{0}+\Delta h-V t\right)$ , where $\Delta h \sim h_{0} \ll L$ . There is no flow in the $z$ direction, and all variation in $z$ may be neglected. There is no applied pressure gradient in the $x$ direction.

Assuming that $V$ is so small that lubrication theory applies, derive an expression for the horizontal volume flux $Q(x)$ at $t=0$ , in terms of the pressure gradient. Show that mass conservation implies that $d Q / d x=V$ , so that $Q(L)-Q(-L)=2 V L$ . Derive another relation between $Q(L)$ and $Q(-L)$ by setting the pressures at $x=\pm L$ to be equal, and hence show that

Q(\pm L)=V L\left(\frac{\Delta h}{h_{0}} \pm 1\right)

Show that lubrication theory applies if $V \ll \mu / h_{0} \rho$ .

Paper 3, Section II, A

Part II, 2010

The equation for the vorticity $\omega(x, y)$ in two-dimensional incompressible flow takes the form

\frac{\partial \omega}{\partial t}+u \frac{\partial \omega}{\partial x}+v \frac{\partial \omega}{\partial y}=\nu\left(\frac{\partial^{2} \omega}{\partial x^{2}}+\frac{\partial^{2} \omega}{\partial y^{2}}\right)

where

u=\frac{\partial \psi}{\partial y}, \quad v=-\frac{\partial \psi}{\partial x} \quad \text { and } \quad \omega=-\left(\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{\partial^{2} \psi}{\partial y^{2}}\right)

and $\psi(x, y)$ is the stream function.

Show that this equation has a time-dependent similarity solution of the form

\psi=C x H(t)^{-1} \phi(\eta), \quad \omega=-C x H(t)^{-3} \phi_{\eta \eta}(\eta) \quad \text { for } \quad \eta=y H(t)^{-1}

if $H(t)=\sqrt{2 C t}$ and $\phi$ satisfies the equation

3 \phi_{\eta \eta}+\eta \phi_{\eta \eta \eta}-\phi_{\eta} \phi_{\eta \eta}+\phi \phi_{\eta \eta \eta}+\frac{1}{R} \phi_{\eta \eta \eta \eta}=0

and $R=C / \nu$ is the effective Reynolds number.

Show that this solution is appropriate for the problem of two-dimensional flow between the rigid planes $y=\pm H(t)$ , and determine the boundary conditions on $\phi$ in that case.

Verify that $(*)$ has exact solutions, satisfying the boundary conditions, of the form

\phi=\frac{(-1)^{k}}{k \pi} \sin (k \pi \eta)-\eta, \quad k=1,2, \ldots

when $R=k^{2} \pi^{2} / 4$ . Sketch this solution when $k$ is large, and discuss whether such solutions are likely to be realised in practice.

Paper 4, Section II, A

Part II, 2010

An axisymmetric incompressible Stokes flow has the Stokes stream function $\Psi(R, \theta)$ in spherical polar coordinates $(R, \theta, \phi)$ . Give expressions for the components $u_{R}, u_{\theta}$ of the flow field in terms of $\Psi$ . Show that the equation satisfied by $\Psi$ is

\mathcal{D}^{2}\left(\mathcal{D}^{2} \Psi\right)=0, \quad \text { where } \quad \mathcal{D}^{2}=\frac{\partial^{2}}{\partial R^{2}}+\frac{\sin \theta}{R^{2}} \frac{\partial}{\partial \theta}\left(\frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\right)

Fluid is contained between the two spheres $R=a, R=b$ , with $b \gg a$ . The fluid velocity vanishes on the outer sphere, while on the inner sphere $u_{R}=U \cos \theta, u_{\theta}=0$ . It is assumed that Stokes flow applies.

(i) Show that the Stokes stream function,

\Psi(R, \theta)=a^{2} U \sin ^{2} \theta\left(A\left(\frac{a}{R}\right)+B\left(\frac{R}{a}\right)+C\left(\frac{R}{a}\right)^{2}+D\left(\frac{R}{a}\right)^{4}\right)

is the general solution of $(*)$ proportional to $\sin ^{2} \theta$ and write down the conditions on $A, B, C, D$ that allow all the boundary conditions to be satisfied.

(ii) Now let $b \rightarrow \infty$ , with $|\mathbf{u}| \rightarrow 0$ as $R \rightarrow \infty$ . Show that $A=B=1 / 4$ with $C=D=0$ .

(iii) Show that when $b / a$ is very large but finite, then the coefficients have the approximate form

C \approx-\frac{3}{8} \frac{a}{b}, \quad D \approx \frac{1}{8} \frac{a^{3}}{b^{3}}, \quad A \approx \frac{1}{4}-\frac{3}{16} \frac{a}{b}, \quad B \approx \frac{1}{4}+\frac{9}{16} \frac{a}{b}

Paper 1, Section I, E

Part II, 2010

Let the complex-valued function $f(z)$ be analytic in the neighbourhood of the point $z_{0}$ and let $u(x, y)$ be the real part of $f(z)$ . Show that

f(z)=2 u\left(\frac{z+\bar{z}_{0}}{2}, \frac{z-\bar{z}_{0}}{2 i}\right)-\overline{f\left(z_{0}\right)}, \quad z=x+i y

Hence find the analytic function whose real part is

e^{-y}[x \cos x-y \sin x]

Paper 2, Section I, E

Part II, 2010

Define

F^{\pm}(x)=\lim _{\epsilon \rightarrow 0} \frac{1}{2 \pi i} \int_{-\infty}^{\infty} \frac{f(t)}{t-(x \pm i \epsilon)} d t, \quad x \in \mathbb{R}

Using the fact that

F^{\pm}(x)=\pm \frac{f(x)}{2}+\frac{1}{2 \pi i} P \int_{-\infty}^{\infty} \frac{f(t)}{t-x} d t, \quad x \in \mathbb{R}

where $P$ denotes the Cauchy principal value, find two complex-valued functions $F^{+}(z)$ and $F^{-}(z)$ which satisfy the following conditions

$F^{+}(z)$ and $F^{-}(z)$ are analytic for $\operatorname{Im} z>0$ and $\operatorname{Im} z<0$ respectively, $z=x+i y$ ;
$F^{+}(x)-F^{-}(x)=\frac{\sin x}{x}, \quad x \in \mathbb{R}$ ;
$F^{\pm}(z)=\mathrm{O}\left(\frac{1}{z}\right), \quad z \rightarrow \infty, \quad \operatorname{Im} z \neq 0$ .

Paper 3, Section I, E

Part II, 2010

Let $\Gamma(z)$ and $\zeta(z)$ denote the gamma and the zeta functions respectively, namely

\begin{aligned} &\Gamma(z)=\int_{0}^{\infty} x^{z-1} e^{-x} d x, \quad \operatorname{Re} z>0 \\ &\zeta(z)=\sum_{m=1}^{\infty} \frac{1}{m^{z}}, \quad \operatorname{Re} z>1 \end{aligned}

By employing a series expansion of $\left(1-e^{-x}\right)^{-2}$ , prove the following identity

\int_{0}^{\infty} \frac{x^{z}}{\left(e^{x}-1\right)^{2}} d x=\Gamma(z+1)[\zeta(z)-\zeta(z+1)], \quad \operatorname{Re} z>1

Paper 4, Section $I$ , E

Part II, 2010

The hypergeometric function $F(a, b ; c ; z)$ can be expressed in the form

F(a, b ; c ; z)=\frac{\Gamma(c)}{\Gamma(b) \Gamma(c-b)} \int_{0}^{1} t^{b-1}(1-t)^{c-b-1}(1-t z)^{-a} d t

for appropriate restrictions on $c, b, z$ .

Express the following integral in terms of a combination of hypergeometric functions

I(u, A)=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{e^{i t(u+1)}}{e^{i t}+i A} d t, \quad|A|>1

[You may use without proof that $\Gamma(z+1)=z \Gamma(z) .$ ]

Paper 1, Section II, E

Part II, 2010

Consider the partial differential equation for $u(x, t)$ ,

\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}+\beta \frac{\partial u}{\partial x}, \quad \beta>0, \quad 0<x<\infty, \quad t>0

where $u(x, t)$ is required to vanish rapidly for all $t$ as $x \rightarrow \infty$ .

(i) Verify that the PDE $(*)$ can be written in the following form

\left(e^{-i k x+\left(k^{2}-i \beta k\right) t} u\right)_{t}=\left(e^{-i k x+\left(k^{2}-i \beta k\right) t}\left[(i k+\beta) u+u_{x}\right]\right)_{x}

(ii) Define $\hat{u}(k, t)=\int_{0}^{\infty} e^{-i k x} u(x, t) d x$ , which is analytic for $\operatorname{Im} k \leqslant 0$ . Determine $\hat{u}(k, t)$ in terms of $\hat{u}(k, 0)$ and also the functions $f_{0}, f_{1}$ defined by

f_{0}(\omega, t)=\int_{0}^{t} e^{-\omega\left(t-t^{\prime}\right)} u\left(0, t^{\prime}\right) d t^{\prime}, \quad f_{1}(\omega, t)=\int_{0}^{t} e^{-\omega\left(t-t^{\prime}\right)} u_{x}\left(0, t^{\prime}\right) d t^{\prime}

(iii) Show that in the inverse transform expression for $u(x, t)$ the integrals involving $f_{0}, f_{1}$ may be transformed to the contour

L=\left\{k \in \mathbb{C}: \operatorname{Re}\left(k^{2}-i \beta k\right)=0, \operatorname{Im} k \geqslant \beta\right\}

By considering $\hat{u}\left(k^{\prime}, t\right)$ where $k^{\prime}=-k+i \beta$ and $k \in L$ , show that it is possible to obtain an equation which allows $f_{1}$ to be eliminated.

(iv) Obtain an integral expression for the solution of $(*)$ subject to the the initialboundary value conditions of given $u(x, 0), u(0, t)$ .

[You need to show that

\int_{L} e^{i k x} \hat{u}\left(k^{\prime}, t\right) d k=0, \quad x>0,

by an appropriate closure of the contour which should be justified.]

Paper 2, Section II, 14E

Part II, 2010

Let

I(z)=i \oint_{C} \frac{u^{z-1}}{u^{2}-4 u+1} d u

where $C$ is a closed anti-clockwise contour which consists of the unit circle joined to a loop around a branch cut along the negative axis between $-1$ and 0 . Show that

I(z)=F(z)+G(z)

where

F(z)=2 \sin (\pi z) \int_{0}^{1} \frac{x^{z-1}}{x^{2}+4 x+1} d x, \quad \operatorname{Re} z>0

and

G(z)=\frac{1}{2} \int_{-\pi}^{\pi} \frac{e^{i(z-1) \theta}}{1+2 \sin ^{2} \frac{\theta}{2}} d \theta, \quad z \in \mathbb{C}

Evaluate $I(z)$ using Cauchy's theorem. Explain how this may be used to obtain an analytic continuation of $F(z)$ valid for all $z \in \mathbb{C}$ .

Paper 3, Section II, H

Part II, 2010

Suppose $X$ is a finite simplicial complex and that $H_{*}(X)$ is a free abelian group for each value of $*$ . Using the Mayer-Vietoris sequence or otherwise, compute $H_{*}\left(S^{1} \times X\right)$ in terms of $H_{*}(X)$ . Use your result to compute $H_{*}\left(T^{n}\right)$ .

[Note that $T^{n}=S^{1} \times \ldots \times S^{1}$ , where there are $n$ factors in the product.]

Paper 1, Section II, 18H

Part II, 2010

Let $\mathbb{F}_{q}$ be a finite field with $q$ elements and $\overline{\mathbb{F}}_{q}$ its algebraic closure.

(i) Give a non-zero polynomial $P(X)$ in $\mathbb{F}_{q}\left[X_{1}, \ldots, X_{n}\right]$ such that

P\left(\alpha_{1}, \ldots, \alpha_{n}\right)=0 \quad \text { for all } \alpha_{1}, \ldots, \alpha_{n} \in \mathbb{F}_{q}

(ii) Show that every irreducible polynomial $P(X)$ of degree $n>0$ in $\mathbb{F}_{q}[X]$ can be factored in $\overline{\mathbb{F}}_{q}[X]$ as $(X-\alpha)\left(X-\alpha^{q}\right)\left(X-\alpha^{q^{2}}\right) \cdots\left(X-\alpha^{q^{n-1}}\right)$ for some $\alpha \in \overline{\mathbb{F}}_{q}$ . What is the splitting field and the Galois group of $P$ over $\mathbb{F}_{q}$ ?

(iii) Let $n$ be a positive integer and $\Phi_{n}(X)$ be the $n$ -th cyclotomic polynomial. Recall that if $K$ is a field of characteristic prime to $n$ , then the set of all roots of $\Phi_{n}$ in $K$ is precisely the set of all primitive $n$ -th roots of unity in $K$ . Using this fact, prove that if $p$ is a prime number not dividing $n$ , then $p$ divides $\Phi_{n}(x)$ in $\mathbb{Z}$ for some $x \in \mathbb{Z}$ if and only if $p=a n+1$ for some integer $a$ . Write down $\Phi_{n}$ explicitly for three different values of $n$ larger than 2 , and give an example of $x$ and $p$ as above for each $n$ .

Paper 2, Section II, H

Part II, 2010

(1) Let $F=\mathbb{Q}(\sqrt[3]{5}, \sqrt{5}, i)$ . What is the degree of $F / \mathbb{Q}$ ? Justify your answer.

(2) Let $F$ be a splitting field of $X^{4}-5$ over $\mathbb{Q}$ . Determine the Galois group $\operatorname{Gal}(F / \mathbb{Q})$ . Determine all the subextensions of $F / \mathbb{Q}$ , expressing each in the form $\mathbb{Q}(x)$ or $\mathbb{Q}(x, y)$ for some $x, y \in F$ .

[Hint: If an automorphism $\rho$ of a field $X$ has order 2 , then for every $x \in X$ the element $x+\rho(x)$ is fixed by $\rho$ .]

Paper 3, Section II, H

Part II, 2010

Let $K$ be a field of characteristic 0 . It is known that soluble extensions of $K$ are contained in a succession of cyclotomic and Kummer extensions. We will refine this statement.

Let $n$ be a positive integer. The $n$ -th cyclotomic field over a field $K$ is denoted by $K\left(\boldsymbol{\mu}_{n}\right)$ . Let $\zeta_{n}$ be a primitive $n$ -th root of unity in $K\left(\boldsymbol{\mu}_{n}\right)$ .

(i) Write $\zeta_{3} \in \mathbb{Q}\left(\boldsymbol{\mu}_{3}\right), \zeta_{5} \in \mathbb{Q}\left(\boldsymbol{\mu}_{5}\right)$ in terms of radicals. Write $\mathbb{Q}\left(\boldsymbol{\mu}_{3}\right) / \mathbb{Q}$ and $\mathbb{Q}\left(\boldsymbol{\mu}_{5}\right) / \mathbb{Q}$ as a succession of Kummer extensions.

(ii) Let $n>1$ , and $F:=K\left(\zeta_{1}, \zeta_{2}, \ldots, \zeta_{n-1}\right)$ . Show that $F\left(\boldsymbol{\mu}_{n}\right) / F$ can be written as a succession of Kummer extensions, using the structure theorem of finite abelian groups (in other words, roots of unity can be written in terms of radicals). Show that every soluble extension of $K$ is contained in a succession of Kummer extensions.

Paper 4, Section II, H

Part II, 2010

Let $K$ be a field of characteristic $\neq 2,3$ , and assume that $K$ contains a primitive cubic root of unity $\zeta$ . Let $P \in K[X]$ be an irreducible cubic polynomial, and let $\alpha, \beta, \gamma$ be its roots in the splitting field $F$ of $P$ over $K$ . Recall that the Lagrange resolvent $x$ of $P$ is defined as $x=\alpha+\zeta \beta+\zeta^{2} \gamma$ .

(i) List the possibilities for the group $\operatorname{Gal}(F / K)$ , and write out the set $\{\sigma(x) \mid \sigma \in \operatorname{Gal}(F / K)\}$ in each case.

(ii) Let $y=\alpha+\zeta \gamma+\zeta^{2} \beta$ . Explain why $x^{3}, y^{3}$ must be roots of a quadratic polynomial in $K[X]$ . Compute this polynomial for $P=X^{3}+b X+c$ , and deduce the criterion to identify $\operatorname{Gal}(F / K)$ through the element $-4 b^{3}-27 c^{2}$ of $K$ .

Paper 1, Section II, B

General Relativity

Part II, 2010

Consider a spacetime $\mathcal{M}$ with a metric $g_{a b}\left(x^{c}\right)$ and a corresponding connection $\Gamma_{b c}^{a}$ . Write down the differential equation satisfied by a geodesic $x^{a}(\lambda)$ , where $\lambda$ is an affine parameter.

Show how the requirement that

\delta \int g_{a b}\left(x^{c}\right) \frac{d}{d \lambda} x^{a}(\lambda) \frac{d}{d \lambda} x^{b}(\lambda) d \lambda=0

where $\delta$ denotes variation of the path, gives the geodesic equation and determines $\Gamma_{b c}^{a}$ .

Show that the timelike geodesics for the 2 -manifold with line element

d s^{2}=t^{-2}\left(d x^{2}-d t^{2}\right)

are given by

t^{2}=x^{2}+\alpha x+\beta

where $\alpha$ and $\beta$ are constants.

Paper 2, Section II, B

General Relativity

Part II, 2010

A vector field $k^{a}$ which satisfies

k_{a ; b}+k_{b ; a}=0

is called a Killing vector field. Prove that $k^{a}$ is a Killing vector field if and only if

k^{c} g_{a b, c}+k_{, b}^{c} g_{a c}+k_{, a}^{c} g_{b c}=0

Prove also that if $V^{a}$ satisfies

V_{; b}^{a} V^{b}=0

then

\left(V^{a} k_{a}\right)_{, b} V^{b}=0

for any Killing vector field $k^{a}$ .

In the two-dimensional space-time with coordinates $x^{a}=(u, v)$ and line element

d s^{2}=-d u^{2}+u^{2} d v^{2}

verify that $(0,1), e^{-v}\left(1, u^{-1}\right)$ and $e^{v}\left(-1, u^{-1}\right)$ are Killing vector fields. Show, by using $(*)$ with $V^{a}$ the tangent vector to a geodesic, that geodesics in this space-time are given by

\alpha e^{v}+\beta e^{-v}=2 \gamma u^{-1}

where $\alpha, \beta$ and $\gamma$ are arbitrary real constants.

Paper 4, Section II, B

General Relativity

Part II, 2010

The Schwarzschild line element is given by

d s^{2}=-F d t^{2}+F^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)

where $F=1-r_{s} / r$ and $r_{s}$ is the Schwarzschild radius. Obtain the equation of geodesic motion of photons moving in the equatorial plane, $\theta=\pi / 2$ , in the form

\left(\frac{d r}{d \tau}\right)^{2}=E^{2}-\frac{h^{2} F}{r^{2}}

where $\tau$ is proper time, and $E$ and $h$ are constants whose physical significance should be indicated briefly.

Defining $u=1 / r$ show that light rays are determined by

\left(\frac{d u}{d \phi}\right)^{2}=\left(\frac{1}{b}\right)^{2}-u^{2}+r_{s} u^{3}

where $b=h / E$ and $r_{s}$ may be taken to be small. Show that, to zeroth order in $r_{s}$ , a light ray is a straight line passing at distance $b$ from the origin. Show that, to first order in $r_{s}$ , the light ray is deflected through an angle $2 r_{s} / b$ . Comment briefly on some observational evidence for the result.

Paper 1, Section I, F

Part II, 2010

Explain what it means to say that $G$ is a crystallographic group of isometries of the Euclidean plane and that $\bar{G}$ is its point group. Prove the crystallographic restriction: a rotation in such a point group $\bar{G}$ must have order $1,2,3,4$ or 6 .

Paper 2, Section I, F

Part II, 2010

Show that a map $T: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ is an isometry for the Euclidean metric on the plane $\mathbb{R}^{2}$ if and only if there is a vector $\boldsymbol{v} \in \mathbb{R}^{2}$ and an orthogonal linear map $B \in \mathrm{O}(2)$ with

T(\boldsymbol{x})=B(\boldsymbol{x})+\boldsymbol{v} \quad \text { for all } \boldsymbol{x} \in \mathbb{R}^{2}

When $T$ is an isometry with $\operatorname{det} B=-1$ , show that $T$ is either a reflection or a glide reflection.

Paper 3, Section I, F

Part II, 2010

Let $U$ be a "triangular" region in the unit disc $\mathbb{D}$ bounded by three hyperbolic geodesics $\gamma_{1}, \gamma_{2}, \gamma_{3}$ that do not meet in $\mathbb{D}$ nor on its boundary. Let $J_{k}$ be inversion in $\gamma_{k}$ and set

A=J_{2} \circ J_{1} ; \quad B=J_{3} \circ J_{2} .

Let $G$ be the group generated by the Möbius transformations $A$ and $B$ . Describe briefly a fundamental set for the group $G$ acting on $\mathbb{D}$ .

Prove that $G$ is a free group on the two generators $A$ and $B$ . Describe the quotient surface $\mathbb{D} / G$ .

Paper 4, Section II, $\mathbf{2 1 H}$

Part II, 2010

State the Snake Lemma. Explain how to define the boundary map which appears in it, and check that it is well-defined. Derive the Mayer-Vietoris sequence from the Snake Lemma.

Given a chain complex $C$ , let $A \subset C$ be the span of all elements in $C$ with grading greater than or equal to $n$ , and let $B \subset C$ be the span of all elements in $C$ with grading less than $n$ . Give a short exact sequence of chain complexes relating $A, B$ , and $C$ . What is the boundary map in the corresponding long exact sequence?

Paper 4, Section I, F

Part II, 2010

Define loxodromic transformations and explain how to determine when a Möbius transformation

T: z \mapsto \frac{a z+b}{c z+d} \quad \text { with } \quad a d-b c=1

is loxodromic.

Show that any Möbius transformation that maps a disc $\Delta$ onto itself cannot be loxodromic.

Paper 1, Section II, F

Part II, 2010

For which circles $\Gamma$ does inversion in $\Gamma$ interchange 0 and $\infty$ ?

Let $\Gamma$ be a circle that lies entirely within the unit $\operatorname{disc} \mathbb{D}=\{z \in \mathbb{C}:|z|<1\} .$ Let $K$ be inversion in this circle $\Gamma$ , let $J$ be inversion in the unit circle, and let $T$ be the Möbius transformation $K \circ J$ . Show that, if $z_{0}$ is a fixed point of $T$ , then

J\left(z_{0}\right)=K\left(z_{0}\right)

and this point is another fixed point of $T$ .

By applying a suitable isometry of the hyperbolic plane $\mathbb{D}$ , or otherwise, show that $\Gamma$ is the set of points at a fixed hyperbolic distance from some point of $\mathbb{D}$ .

Paper 4, Section II, F

Part II, 2010

Explain briefly how Möbius transformations of the Riemann sphere are extended to give isometries of the unit ball $B^{3} \subset \mathbb{R}^{3}$ for the hyperbolic metric.

Which Möbius transformations have extensions that fix the origin in $B^{3}$ ?

For which Möbius transformations $T$ can we find a hyperbolic line in $B^{3}$ that $T$ maps onto itself? For which of these Möbius transformations is there only one such hyperbolic line?

Paper 1, Section II, F

Part II, 2010

(a) Define the Ramsey number $R(s)$ . Show that for all integers $s \geqslant 2$ the Ramsey number $R(s)$ exists and that $R(s) \leqslant 4^{s}$ .

(b) For any graph $G$ , let $R(G)$ denote the least positive integer $n$ such that in any red-blue colouring of the edges of the complete graph $K_{n}$ there must be a monochromatic copy of $G$ .

(i) How do we know that $R(G)$ exists for every graph $G$ ?

(ii) Let $s$ be a positive integer. Show that, whenever the edge of $K_{2 s}$ are red-blue coloured, there must be a monochromatic copy of the complete bipartite graph $K_{1, s}$ .

(iii) Suppose $s$ is odd. By exhibiting a suitable colouring of $K_{2 s-1}$ , show that $R\left(K_{1, s}\right)=2 s$ .

(iv) Suppose instead $s$ is even. What is $R\left(K_{1, s}\right) ?$ Justify your answer.

Paper 2, Section II, F

Part II, 2010

Let $G$ be a bipartite graph with vertex classes $X$ and $Y$ . What does it mean to say that $G$ contains a matching from $X$ to $Y$ ?

State and prove Hall's Marriage Theorem, giving a necessary and sufficient condition for $G$ to contain a matching from $X$ to $Y$ .

Now assume that $G$ does contain a matching (from $X$ to $Y$ ). For a subset $A \subset X$ , $\Gamma(A)$ denotes the set of vertices adjacent to some vertex in $A$ .

(i) Suppose $|\Gamma(A)|>|A|$ for every $A \subset X$ with $A \neq \emptyset, X$ . Show that every edge of $G$ is contained in a matching.

(ii) Suppose that every edge of $G$ is contained in a matching and that $G$ is connected. Show that $|\Gamma(A)|>|A|$ for every $A \subset X$ with $A \neq \emptyset, X$ .

(iii) For each $n \geqslant 2$ , give an example of $G$ with $|X|=n$ such that every edge is contained in a matching but $|\Gamma(A)|=|A|$ for some $A \subset X$ with $A \neq \emptyset, X$ .

(iv) Suppose that every edge of $G$ is contained in a matching. Must every pair of independent edges in $G$ be contained in a matching? Give a proof or counterexample as appropriate.

[No form of Menger's Theorem or of the Max-Flow-Min-Cut Theorem may be assumed without proof.]

Paper 3, Section II, F

Part II, 2010

Let $G$ be a graph of order $n$ . Show that $G$ must contain an independent set of $\left\lceil\sum_{v \in G} \frac{1}{d(v)+1}\right]$ vertices (where $\lceil x\rceil$ denotes the least integer $\left.\geqslant x\right)$ .

[Hint: take a random ordering of the vertices of $G$ , and consider the set of those vertices which are adjacent to no earlier vertex in the ordering.]

Fix an integer $m<n$ with $m$ dividing $n$ , and suppose that $e(G)=m\left(\begin{array}{c}n / m \\ 2\end{array}\right)$ .

(i) Deduce that $G$ must contain an independent set of $m$ vertices.

(ii) Must $G$ contain an independent set of $m+1$ vertices?

Paper 4, Section II, F

Part II, 2010

State Euler's formula relating the number of vertices, edges and faces in a drawing of a connected planar graph. Deduce that every planar graph has chromatic number at most $5 .$

Show also that any triangle-free planar graph has chromatic number at most 4 .

Suppose $G$ is a planar graph which is minimal 5 -chromatic; that is to say, $\chi(G)=5$ but if $H$ is a subgraph of $G$ with $H \neq G$ then $\chi(H)<5$ . Prove that $\delta(G) \geqslant 5$ . Does this remain true if we drop the assumption that $G$ is planar? Justify your answer.

[The Four Colour Theorem may not be assumed.]

Paper 1, Section II, E

Integrable Systems

Part II, 2010

Define a Poisson structure on an open set $U \subset \mathbb{R}^{n}$ in terms of an anti-symmetric matrix $\omega^{a b}: U \longrightarrow \mathbb{R}$ , where $a, b=1, \cdots, n$ . By considering the Poisson brackets of the coordinate functions $x^{a}$ show that

\sum_{d=1}^{n}\left(\omega^{d c} \frac{\partial \omega^{a b}}{\partial x^{d}}+\omega^{d b} \frac{\partial \omega^{c a}}{\partial x^{d}}+\omega^{d a} \frac{\partial \omega^{b c}}{\partial x^{d}}\right)=0

Now set $n=3$ and consider $\omega^{a b}=\sum_{c=1}^{3} \varepsilon^{a b c} x^{c}$ , where $\varepsilon^{a b c}$ is the totally antisymmetric symbol on $\mathbb{R}^{3}$ with $\varepsilon^{123}=1$ . Find a non-constant function $f: \mathbb{R}^{3} \longrightarrow \mathbb{R}$ such that

\left\{f, x^{a}\right\}=0, \quad a=1,2,3

Consider the Hamiltonian

H\left(x^{1}, x^{2}, x^{3}\right)=\frac{1}{2} \sum_{a, b=1}^{3} M^{a b} x^{a} x^{b}

where $M^{a b}$ is a constant symmetric matrix and show that the Hamilton equations of motion with $\omega^{a b}=\sum_{c=1}^{3} \varepsilon^{a b c} x^{c}$ are of the form

\dot{x}^{a}=\sum_{b, c=1}^{3} Q^{a b c} x^{b} x^{c},

where the constants $Q^{a b c}$ should be determined in terms of $M^{a b}$ .

Paper 2, Section II, E

Integrable Systems

Part II, 2010

Consider the Gelfand-Levitan-Marchenko (GLM) integral equation

K(x, y)+F(x+y)+\int_{x}^{\infty} K(x, z) F(z+y) d z=0

with $F(x)=\sum_{1}^{N} \beta_{n} e^{-c_{n} x}$ , where $c_{1}, \ldots, c_{N}$ are positive constants and $\beta_{1}, \ldots, \beta_{N}$ are constants. Consider separable solutions of the form

K(x, y)=\sum_{n=1}^{N} K_{n}(x) e^{-c_{n} y}

and reduce the GLM equation to a linear system

\sum_{m=1}^{N} A_{n m}(x) K_{m}(x)=B_{n}(x)

where the matrix $A_{n m}(x)$ and the vector $B_{n}(x)$ should be determined.

How is $K$ related to solutions of the $K d V$ equation?

Set $N=1, c_{1}=c, \beta_{1}=\beta \exp \left(8 c^{3} t\right)$ where $c, \beta$ are constants. Show that the corresponding one soliton solution of the $\mathrm{KdV}$ equation is given by

u(x, t)=-\frac{4 \beta_{1} c e^{-2 c x}}{\left(1+\left(\beta_{1} / 2 c\right) e^{-2 c x}\right)^{2}}

[You may use any facts about the Inverse Scattering Transform without proof.]

Paper 3, Section II, E

Integrable Systems

Part II, 2010

Consider a vector field

V=\alpha x \frac{\partial}{\partial x}+\beta t \frac{\partial}{\partial t}+\gamma v \frac{\partial}{\partial v}

on $\mathbb{R}^{3}$ , where $\alpha, \beta$ and $\gamma$ are constants. Find the one-parameter group of transformations generated by this vector field.

Find the values of the constants $(\alpha, \beta, \gamma)$ such that $V$ generates a Lie point symmetry of the modified $\mathrm{KdV}$ equation ( $\mathrm{KKdV}$ )

v_{t}-6 v^{2} v_{x}+v_{x x x}=0, \quad \text { where } \quad v=v(x, t)

Show that the function $u=u(x, t)$ given by $u=v^{2}+v_{x}$ satisfies the KdV equation and find a Lie point symmetry of $\mathrm{KdV}$ corresponding to the Lie point symmetry of $\mathrm{mKdV}$ which you have determined from $V$ .

Paper 1, Section II, B

Part II, 2010

Give an account of the variational principle for establishing an upper bound on the ground-state energy, $E_{0}$ , of a particle moving in a potential $V(x)$ in one dimension.

Explain how an upper bound on the energy of the first excited state can be found in the case that $V(x)$ is a symmetric function.

A particle of mass $2 m=\hbar^{2}$ moves in the potential

V(x)=-V_{0} e^{-x^{2}}, \quad V_{0}>0

Use the trial wavefunction

\psi(x)=e^{-\frac{1}{2} a x^{2}}

where $a$ is a positive real parameter, to establish the upper bound $E_{0} \leqslant E(a)$ for the energy of the ground state, where

E(a)=\frac{1}{2} a-V_{0} \frac{\sqrt{a}}{\sqrt{1+a}} .

Show that, for $a>0, E(a)$ has one zero and find its position.

Show that the turning points of $E(a)$ are given by

(1+a)^{3}=\frac{V_{0}^{2}}{a}

and deduce that there is one turning point in $a>0$ for all $V_{0}>0$ .

Sketch $E(a)$ for $a>0$ and hence deduce that $V(x)$ has at least one bound state for all $V_{0}>0$ .

For $0<V_{0} \ll 1$ show that

-V_{0}<E_{0} \leqslant \epsilon\left(V_{0}\right),

where $\epsilon\left(V_{0}\right)=-\frac{1}{2} V_{0}^{2}+\mathrm{O}\left(V_{0}^{4}\right)$ .

[You may use the result that $\int_{-\infty}^{\infty} e^{-b x^{2}} d x=\sqrt{\frac{\pi}{b}}$ for $b>0 .$ ]

Paper 1, Section II, H

Part II, 2010

a) State and prove the Banach-Steinhaus Theorem.

[You may use the Baire Category Theorem without proving it.]

b) Let $X$ be a (complex) normed space and $S \subset X$ . Prove that if $\{f(x): x \in S\}$ is a bounded set in $\mathbb{C}$ for every linear functional $f \in X^{*}$ then there exists $K \geqslant 0$ such that $\|x\| \leqslant K$ for all $x \in S .$

[You may use here the following consequence of the Hahn-Banach Theorem without proving it: for a given $x \in X$ , there exists $f \in X^{*}$ with $\|f\|=1$ and $|f(x)|=\|x\|$ .]

c) Conclude that if two norms $\|\cdot\|_{1}$ and $\|\cdot\|_{2}$ on a (complex) vector space $V$ are not equivalent, there exists a linear functional $f: V \rightarrow \mathbb{C}$ which is continuous with respect to one of the two norms, and discontinuous with respect to the other.

Paper 2, Section II, H

Part II, 2010

For a sequence $x=\left(x_{1}, x_{2}, \ldots\right)$ with $x_{j} \in \mathbb{C}$ for all $j \geqslant 1$ , let

\|x\|_{\infty}:=\sup _{j \geqslant 1}\left|x_{j}\right|

and $\ell^{\infty}=\left\{x=\left(x_{1}, x_{2}, \ldots\right): x_{j} \in \mathbb{C}\right.$ for all $j \geqslant 1$ and $\left.\|x\|_{\infty}<\infty\right\}$ .

a) Prove that $\ell^{\infty}$ is a Banach space.

b) Define

c_{0}=\left\{x=\left(x_{1}, x_{2}, \ldots\right) \in \ell^{\infty}: \lim _{j \rightarrow \infty} x_{j}=0\right\}

and

\ell^{1}=\left\{x=\left(x_{1}, x_{2}, \ldots\right): x_{j} \in \mathbb{C} \text { for all } j \in \mathbb{N} \text { and }\|x\|_{1}=\sum_{\ell=1}^{\infty}\left|x_{\ell}\right|<\infty\right\}

Show that $c_{0}$ is a closed subspace of $\ell^{\infty}$ . Show that $c_{0}^{*} \simeq \ell^{1}$ .

[Hint: find an isometric isomorphism from $\ell^{1}$ to $\left.c_{0}^{*} .\right]$

c) Let

c_{00}=\left\{x=\left(x_{1}, x_{2}, \ldots\right) \in \ell^{\infty}: x_{j}=0 \text { for all } j \text { large enough }\right\} .

Is $c_{00}$ a closed subspace of $\ell^{\infty} ?$ If not, what is the closure of $c_{00} ?$

Paper 3, Section II, H

Part II, 2010

State and prove the Stone-Weierstrass theorem for real-valued functions.

[You may use without proof the fact that the function $s \rightarrow|s|$ can be uniformly approximated by polynomials on $[-1,1] .]$

Paper 4, Section II, H

Part II, 2010

Let $X$ be a Banach space.

a) What does it mean for a bounded linear map $T: X \rightarrow X$ to be compact?

b) Let $\mathcal{B}(X)$ be the Banach space of all bounded linear maps $S: X \rightarrow X$ . Let $\mathcal{B}_{0}(X)$ be the subset of $\mathcal{B}(X)$ consisting of all compact operators. Show that $\mathcal{B}_{0}(X)$ is a closed subspace of $\mathcal{B}(X)$ . Show that, if $S \in \mathcal{B}(X)$ and $T \in \mathcal{B}_{0}(X)$ , then $S T, T S \in \mathcal{B}_{0}(X)$ .

c) Let

X=\ell^{2}=\left\{x=\left(x_{1}, x_{2}, \ldots\right): x_{j} \in \mathbb{C} \quad \text { and } \quad\|x\|_{2}^{2}=\sum_{j=1}^{\infty}\left|x_{j}\right|^{2}<\infty\right\}

and $T: X \rightarrow X$ be defined by

(T x)_{k}=\frac{x_{k+1}}{k+1} .

Is $T$ compact? What is the spectrum of $T ?$ Explain your answers.

Paper 1, Section II, G

Part II, 2010

Show that $\aleph_{\alpha}^{2}=\aleph_{\alpha}$ for all $\alpha$ .

An infinite cardinal $m$ is called regular if it cannot be written as a sum of fewer than $m$ cardinals each of which is smaller than $m$ . Prove that $\aleph_{0}$ and $\aleph_{1}$ are regular.

Is $\aleph_{2}$ regular? Is $\aleph_{\omega}$ regular? Justify your answers.

Paper 2, Section II, G

Part II, 2010

Let $\alpha$ be a non-zero ordinal. Prove that there exists a greatest ordinal $\beta$ such that $\omega^{\beta} \leqslant \alpha$ . Explain why there exists an ordinal $\gamma$ with $\omega^{\beta}+\gamma=\alpha$ . Prove that $\gamma$ is unique, and that $\gamma<\alpha$ .

A non-zero ordinal $\alpha$ is called decomposable if it can be written as the sum of two smaller non-zero ordinals. Deduce that if $\alpha$ is not a power of $\omega$ then $\alpha$ is decomposable.

Conversely, prove that if $\alpha$ is a power of $\omega$ then $\alpha$ is not decomposable.

[Hint: consider the cases $\alpha=\omega^{\beta}$ ( $\beta$ a successor) and $\alpha=\omega^{\beta}$ ( $\beta$ a limit) separately.]

Paper 3, Section II, G

Part II, 2010

Define the sets $V_{\alpha}, \alpha \in O N$ . What is meant by the rank of a set?

Explain briefly why, for every $\alpha$ , there exists a set of rank $\alpha$ .

Let $x$ be a transitive set of rank $\alpha$ . Show that $x$ has an element of rank $\beta$ for every $\beta<\alpha$ .

For which $\alpha$ does there exist a finite set of rank $\alpha$ ? For which $\alpha$ does there exist a finite transitive set of rank $\alpha$ ? Justify your answers.

[Standard properties of rank may be assumed.]

Paper 4, Section II, G

Part II, 2010

State and prove the Completeness Theorem for Propositional Logic.

[You do not need to give definitions of the various terms involved. You may assume that the set of primitive propositions is countable. You may also assume the Deduction Theorem.]

Explain briefly how your proof should be modified if the set of primitive propositions is allowed to be uncountable.

Paper 1, Section I, A

Part II, 2010

A delay model for a population $N_{t}$ consists of

N_{t+1}=\frac{r N_{t}}{1+b N_{t-1}^{2}}

where $t$ is discrete time, $r>1$ and $b>0$ . Investigate the linear stability about the positive steady state $N^{*}$ . Show that $r=2$ is a bifurcation value at which the steady state bifurcates to a periodic solution of period 6 .

Paper 2, Section $I$ , A

Part II, 2010

The population of a certain species subjected to a specific kind of predation is modelled by the difference equation

u_{t+1}=a \frac{u_{t}^{2}}{b^{2}+u_{t}^{2}}, \quad a>0

Determine the equilibria and show that if $a^{2}>4 b^{2}$ it is possible for the population to be driven to extinction if it becomes less than a critical size which you should find. Explain your reasoning by means of a cobweb diagram.

Paper 2, Section II, B

Part II, 2010

A beam of particles of mass $m$ and momentum $p=\hbar k$ is incident along the $z$ -axis. Write down the asymptotic form of the wave function which describes scattering under the influence of a spherically symmetric potential $V(r)$ and which defines the scattering amplitude $f(\theta)$ .

Given that, for large $r$ ,

e^{i k r \cos \theta} \sim \frac{1}{2 i k r} \sum_{l=0}^{\infty}(2 l+1)\left(e^{i k r}-(-1)^{l} e^{-i k r}\right) P_{l}(\cos \theta),

show how to derive the partial-wave expansion of the scattering amplitude in the form

f(\theta)=\frac{1}{k} \sum_{l=0}^{\infty}(2 l+1) e^{i \delta_{l}} \sin \delta_{l} P_{l}(\cos \theta)

Obtain an expression for the total cross-section, $\sigma$ .

Let $V(r)$ have the form

V(r)=\left\{\begin{array}{cl} -V_{0}, & r<a \\ 0, & r>a \end{array}\right.

where $V_{0}=\frac{\hbar^{2}}{2 m} \gamma^{2}$

Show that the $l=0$ phase-shift $\delta_{0}$ satisfies

\frac{\tan \left(k a+\delta_{0}\right)}{k a}=\frac{\tan \kappa a}{\kappa a},

where $\kappa^{2}=k^{2}+\gamma^{2}$ .

Assume $\gamma$ to be large compared with $k$ so that $\kappa$ may be approximated by $\gamma$ . Show, using graphical methods or otherwise, that there are values for $k$ for which $\delta_{0}(k)=n \pi$ for some integer $n$ , which should not be calculated. Show that the smallest value, $k_{0}$ , of $k$ for which this condition holds certainly satisfies $k_{0}<3 \pi / 2 a$ .

Paper 3, Section I, A

Part II, 2010

A population of aerobic bacteria swims in a laterally-infinite layer of fluid occupying $-\infty<x<\infty,-\infty<y<\infty$ , and $-d / 2<z<d / 2$ , with the top and bottom surfaces in contact with air. Assuming that there is no fluid motion and that all physical quantities depend only on $z$ , the oxygen concentration $c$ and bacterial concentration $n$ obey the coupled equations

\begin{aligned} \frac{\partial c}{\partial t} &=D_{c} \frac{\partial^{2} c}{\partial z^{2}}-k n \\ \frac{\partial n}{\partial t} &=D_{n} \frac{\partial^{2} n}{\partial z^{2}}-\frac{\partial}{\partial z}\left(\mu n \frac{\partial c}{\partial z}\right) \end{aligned}

Consider first the case in which there is no chemotaxis, so $n$ has the spatially-uniform value $\bar{n}$ . Find the steady-state oxygen concentration consistent with the boundary conditions $c(\pm d / 2)=c_{0}$ . Calculate the Fick's law flux of oxygen into the layer and justify your answer on physical grounds.

Now allowing chemotaxis and cellular diffusion, show that the equilibrium oxygen concentration satisfies

\frac{d^{2} c}{d z^{2}}-\frac{k n_{0}}{D_{c}} \exp \left(\mu c / D_{n}\right)=0

where $n_{0}$ is a suitable normalisation constant that need not be found.

Paper 4, Section I, A

Part II, 2010

A concentration $u(x, t)$ obeys the differential equation

\frac{\partial u}{\partial t}=D u_{x x}+f(u)

in the domain $0 \leqslant x \leqslant L$ , with boundary conditions $u(0, t)=u(L, t)=0$ and initial condition $u(x, 0)=u_{0}(x)$ , and where $D$ is a positive constant. Assume $f(0)=0$ and $f^{\prime}(0)>0$ . Linearising the dynamics around $u=0$ , and representing $u(x, t)$ as a suitable Fourier expansion, show that the condition for the linear stability of $u=0$ can be expressed as the following condition on the domain length

L<\pi\left[\frac{D}{f^{\prime}(0)}\right]^{1 / 2}

Paper 2, Section II, A

Part II, 2010

The radially symmetric spread of an insect population density $n(r, t)$ in the plane is described by the equation

\frac{\partial n}{\partial t}=\frac{D_{0}}{r} \frac{\partial}{\partial r}\left[r\left(\frac{n}{n_{0}}\right)^{2} \frac{\partial n}{\partial r}\right]

Suppose $Q$ insects are released at $r=0$ at $t=0$ . We wish to find a similarity solution to $(*)$ in the form

n(r, t)=\frac{n_{0}}{\lambda^{2}(t)} F\left(\frac{r}{r_{0} \lambda(t)}\right)

Show first that the PDE $(*)$ reduces to an ODE for $F$ if $\lambda(t)$ obeys the equation

\lambda^{5} \frac{d \lambda}{d t}=C \frac{D_{0}}{r_{0}^{2}}

where $C$ is an arbitrary constant (that may be set to unity), and then obtain $\lambda(t)$ and $F$ such that $F(0)=1$ and $F(\xi)=0$ for $\xi \geqslant 1$ . Determine $r_{0}$ in terms of $n_{0}$ and $Q$ . Sketch the function $n(r, t)$ at various times to indicate its qualitative behaviour.

Paper 3, Section II, A

Part II, 2010

Consider an epidemic model in which $S(x, t)$ is the local population density of susceptibles and $I(x, t)$ is the density of infectives

\begin{aligned} &\frac{\partial S}{\partial t}=-r I S \\ &\frac{\partial I}{\partial t}=D \frac{\partial^{2} I}{\partial x^{2}}+r I S-a I \end{aligned}

where $r, a$ , and $D$ are positive. If $S_{0}$ is a characteristic population value, show that the rescalings $I / S_{0} \rightarrow I, S / S_{0} \rightarrow S,\left(r S_{0} / D\right)^{1 / 2} x \rightarrow x, r S_{0} t \rightarrow t$ reduce this system to

\begin{aligned} &\frac{\partial S}{\partial t}=-I S \\ &\frac{\partial I}{\partial t}=\frac{\partial^{2} I}{\partial x^{2}}+I S-\lambda I \end{aligned}

where $\lambda$ should be found.

Travelling wavefront solutions are of the form $S(x, t)=S(z), I(x, t)=I(z)$ , where $z=x-c t$ and $c$ is the wave speed, and we seek solutions with boundary conditions $S(\infty)=1, S^{\prime}(\infty)=0, I(\infty)=I(-\infty)=0$ . Under the travelling-wave assumption reduce the rescaled PDEs to ODEs, and show by linearisation around the leading edge of the advancing front that the requirement that $I$ be non-negative leads to the condition $\lambda<1$ and hence the wave speed relation

c \geqslant 2(1-\lambda)^{1 / 2}, \quad \lambda<1

Using the two ODEs you have obtained, show that the surviving susceptible population fraction $\sigma=S(-\infty)$ after the passage of the front satisfies

\sigma-\lambda \ln \sigma=1,

and sketch $\sigma$ as a function of $\lambda$ .

Paper 1, Section II, G

Number Fields

Part II, 2010

Suppose that $m$ is a square-free positive integer, $m \geqslant 5, m \not \equiv 1 \quad(\bmod 4)$ . Show that, if the class number of $K=\mathbb{Q}(\sqrt{-m})$ is prime to 3 , then $x^{3}=y^{2}+m$ has at most two solutions in integers. Assume the $m$ is even.

Paper 2, Section II, G

Number Fields

Part II, 2010

Calculate the class group of the field $\mathbb{Q}(\sqrt{-14})$ .

Paper 4, Section II, G

Number Fields

Part II, 2010

Suppose that $\alpha$ is a zero of $x^{3}-x+3$ and that $K=\mathbb{Q}(\alpha)$ . Show that $[K: \mathbb{Q}]=3$ . Show that $O_{K}$ , the ring of integers in $K$ , is $O_{K}=\mathbb{Z}[\alpha]$ .

[You may quote any general theorem that you wish, provided that you state it clearly. Note that the discriminant of $x^{3}+p x+q$ is $-4 p^{3}-27 q^{2}$ .]

Paper 1, Section I, G

Part II, 2010

(i) Let $N$ be an integer $\geqslant 2$ . Define the addition and multiplication on the set of congruence classes modulo $N$ .

(ii) Let an integer $M \geqslant 1$ have expansion to the base 10 given by $a_{s} \ldots a_{0}$ . Prove that 11 divides $M$ if and only if $\sum_{i=0}^{s}(-1)^{i} a_{i}$ is divisible by 11 .

Paper 2, Section I, G

Part II, 2010

Let $p$ be an odd prime number. If $n$ is an integer prime to $p$ , define $\left(\frac{n}{p}\right)$ .

(i) Prove that $\chi(n)=\left(\frac{n}{p}\right)$ defines a homomorphism from $(\mathbb{Z} / p \mathbb{Z})^{\times}$ to the group $\{\pm 1\}$ . What is the value of $\chi(-1) ?$

(ii) If $p \equiv 1 \bmod 4$ , prove that $\sum_{n=1}^{p-1} \chi(n) n=0$ .

Paper 3, Section I, G

Part II, 2010

(i) Let $M$ and $N$ be positive integers, such that $N$ is not a perfect square. If $M<\sqrt{N}$ , show that every solution of the equation

x^{2}-N y^{2}=M

in positive integers $x, y$ comes from some convergent of the continued fraction of $\sqrt{N}$ .

(ii) Find a solution in positive integers $x, y$ of

x^{2}-29 y^{2}=5