Paper 3, Section II, I
Cars looking for a parking space are directed to one of three unlimited parking lots A, B and C. First, immediately after the entrance, the road forks: one direction is to lot A, the other to B and C. Shortly afterwards, the latter forks again, between B and C. See the diagram below.
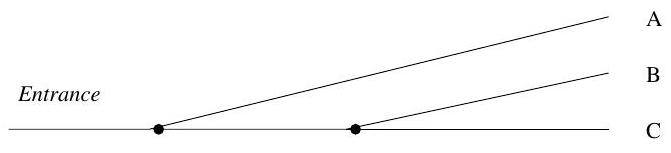
The policeman at the first road fork directs an entering car with probability to A and with probability to the second fork. The policeman at the second fork sends the passing cars to or alternately: cars approaching the second fork go to and cars to .
Assuming that the total arrival process of cars is Poisson of rate , consider the processes and , where is the number of cars directed to lot by time , for . The times for a car to travel from the first to the second fork, or from a fork to the parking lot, are all negligible.
(a) Characterise each of the processes and , by specifying if it is (i) Poisson, (ii) renewal or (iii) delayed renewal. Correspondingly, specify the rate, the holding-time distribution and the distribution of the delay.
(b) In the case of a renewal process, determine the equilibrium delay distribution.
(c) Given , write down explicit expressions for the probability that the interval is free of points in the corresponding process, .