Consider the following sum related to Riemann's zeta function:
S:=m=1∑[2πa]ms−1,s=σ+it,σ,t∈R,a>2π,a=2πN,N∈Z+,
where [a/2π] denotes the integer part of a/2π.
(i) By using an appropriate branch cut, show that
S=(2π)se−2iπs∫Lf(z,s)dz,f(z,s)=1−e−ze−zzs−1
where L is the circle in the complex z-plane centred at i(a+b)/2 with radius (a−b)/2, 0<b<2π.
(ii) Use the above representation to show that, for a>2π and 0<b<2π,
m=1∑[2πa]ms−1=(2π)s1[e−2iπs∫Cbaf(z,s)dz−e2iπs∫C−a−bf(z,s)dz+sas−sbs]
where f(z,s) is defined in (i) and the curves Cba,C−a−b are the following semi-circles in the right half complex z-plane:
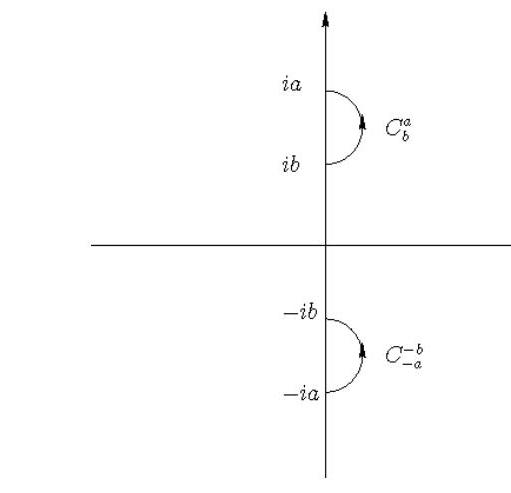
The curves Cba and C−a−b.
CbaC−a−b={2i(a+b)+2(a−b)eiθ,−2π<θ<2π}={2−i(a+b)+2(a−b)eiθ,−2π<θ<2π}
Part II, 2011 List of Questions
[TURN OVER
