Paper 4, Section II, A
Part II, 2012
Setting , the raising and lowering operators for angular momentum satisfy
where . Find the matrix representation for in the basis
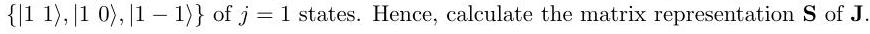
Suppose that the angular momentum of the state is measured in the direction to be . Find the components of , expressing each component by a single term consisting of products of powers of and multiplied by constants.
Suppose that two measurements of a total angular momentum 1 system are made. The first is made in the third direction with value , and the second measurement is subsequently immediately made in direction . What is the probability that the second measurement is also ?