Paper 2, Section II, K
An agent has expected-utility preferences over his possible wealth at time 1 ; that is, the wealth is preferred to wealth if and only if , where the function is strictly concave and twice continuously differentiable. The agent can trade in a market, with the time-1 value of his portfolio lying in an affine space of random variables. Assuming cash can be held between time 0 and time 1 , define the agent's time-0 utility indifference price for a contingent claim with time-1 value . Assuming any regularity conditions you may require, prove that the map is concave.
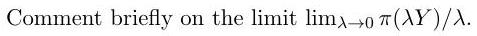
Consider a market with two claims with time-1 values and . Their joint distribution is
At time 0 , arbitrary quantities of the claim can be bought at price , but is not marketed. Derive an explicit expression for in the case where
where is a given constant.