A planar pendulum consists of a mass $m$ at the end of a light rod of length $l$. The pivot of the pendulum is attached to a bead of mass $M$, which slides along a horizontal rod without friction. The bead is connected to the ends of the horizontal rod by two identical springs of force constant $k$. The pivot constrains the pendulum to swing in the vertical plane through the horizontal rod. The horizontal rod is mounted on a bracket, so the system could rotate about the vertical axis which goes through its centre as shown in the figure.

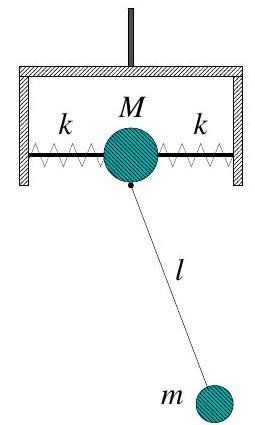
(a) Initially, the system is not allowed to rotate about the vertical axis.

(i) Identify suitable generalized coordinates and write down the Lagrangian of the system.

(ii) Write down expression(s) for any conserved quantities. Justify your answer.

(iii) Derive the equations of motion.

(iv) For $M=m / 2$ and $g m / k l=3$, find the frequencies of small oscillations around the stable equilibrium and the corresponding normal modes. Describe the respective motions of the system.

(b) Assume now that the system is free to rotate about the vertical axis without friction. Write down the Lagrangian of the system. Identify and calculate the additional conserved quantity.