Part II 2015

• Paper 4, Section II, F

  Algebraic Geometry

  Part II, 2015

  (i) Explain how a linear system on a curve $C$ may induce a morphism from $C$ to projective space. What condition on the linear system is necessary to yield a morphism $f: C \rightarrow \mathbb{P}^{n}$ such that the pull-back of a hyperplane section is an element of the linear system? What condition is necessary to imply the morphism is an embedding?

  (ii) State the Riemann-Roch theorem for curves.

  (iii) Show that any divisor of degree 5 on a curve $C$ of genus 2 induces an embedding.

  comment

• Paper 3, Section II, F

  Algebraic Geometry

  Part II, 2015

  (i) Let $X$ be an affine variety. Define the tangent space of $X$ at a point $P$. Say what it means for the variety to be singular at $P$.

  (ii) Find the singularities of the surface in $\mathbb{P}^{3}$ given by the equation

  $$x y z+y z w+z w x+w x y=0 .$$

  (iii) Consider $C=Z\left(x^{2}-y^{3}\right) \subseteq \mathbb{A}^{2}$. Let $X \rightarrow \mathbb{A}^{2}$ be the blowup of the origin. Compute the proper transform of $C$ in $X$, and show it is non-singular.

  comment

• Paper 1, Section II, A

  Applications of Quantum Mechanics

  Part II, 2015

  Define the Rayleigh-Ritz quotient $R[\psi]$ for a normalisable state $|\psi\rangle$ of a quantum system with Hamiltonian $H$. Given that the spectrum of $H$ is discrete and that there is a unique ground state of energy $E_{0}$, show that $R[\psi] \geqslant E_{0}$ and that equality holds if and only if $|\psi\rangle$ is the ground state.

  A simple harmonic oscillator (SHO) is a particle of mass $m$ moving in one dimension subject to the potential

  $$V(x)=\frac{1}{2} m \omega^{2} x^{2}$$

  Estimate the ground state energy $E_{0}$ of the SHO by using the ground state wavefunction for a particle in an infinite potential well of width $a$, centred on the origin (the potential is $U(x)=0$ for $|x|<a / 2$ and $U(x)=\infty$ for $|x|>a / 2)$. Take $a$ as the variational parameter.

  Perform a similar estimate for the energy $E_{1}$ of the first excited state of the SHO by using the first excited state of the infinite potential well as a trial wavefunction.

  Is the estimate for $E_{1}$ necessarily an upper bound? Justify your answer.

  $\left[\right.$ You may use : $\int_{-\pi / 2}^{\pi / 2} y^{2} \cos ^{2} y d y=\frac{\pi}{4}\left(\frac{\pi^{2}}{6}-1\right) \quad$ and $\left.\quad \int_{-\pi}^{\pi} y^{2} \sin ^{2} y d y=\pi\left(\frac{\pi^{2}}{3}-\frac{1}{2}\right) \cdot\right]$

  comment

• Paper 4, Section II, $25 K$

  Optimization and Control

  Part II, 2015

  Consider the scalar system evolving as

  $$x_{t}=x_{t-1}+u_{t-1}+\epsilon_{t}, \quad t=1,2, \ldots,$$

  where $\left\{\epsilon_{t}\right\}_{t=1}^{\infty}$ is a white noise sequence with $E \epsilon_{t}=0$ and $E \epsilon_{t}^{2}=v$. It is desired to choose controls $\left\{u_{t}\right\}_{t=0}^{h-1}$ to minimize $E\left[\sum_{t=0}^{h-1}\left(\frac{1}{2} x_{t}^{2}+u_{t}^{2}\right)+x_{h}^{2}\right]$. Show that for $h=6$ the minimal cost is $x_{0}^{2}+6 v$.

  Find a constant $\lambda$ and a function $\phi$ which solve

  $$\phi(x)+\lambda=\min _{u}\left[\frac{1}{2} x^{2}+u^{2}+E \phi\left(x+u+\epsilon_{1}\right)\right]$$

  Let $P$ be the class of those policies for which every $u_{t}$ obeys the constraint $\left(x_{t}+u_{t}\right)^{2} \leqslant(0.9) x_{t}^{2}$. Show that $E_{\pi} \phi\left(x_{t}\right) \leqslant x_{0}^{2}+10 v$, for all $\pi \in P$. Find, and prove optimal, a policy which over all $\pi \in P$ minimizes

  $$\lim _{h \rightarrow \infty} \frac{1}{h} E_{\pi}\left[\sum_{t=0}^{h-1}\left(\frac{1}{2} x_{t}^{2}+u_{t}^{2}\right)\right]$$

  comment

• Paper 3, Section II, K

  Optimization and Control

  Part II, 2015

  A burglar having wealth $x$ may retire, or go burgling another night, in either of towns 1 or 2 . If he burgles in town $i$ then with probability $p_{i}=1-q_{i}$ he will, independently of previous nights, be caught, imprisoned and lose all his wealth. If he is not caught then his wealth increases by 0 or $2 a_{i}$, each with probability $1 / 2$ and independently of what happens on other nights. Values of $p_{i}$ and $a_{i}$ are the same every night. He wishes to maximize his expected wealth at the point he retires, is imprisoned, or $s$ nights have elapsed.

  Using the dynamic programming equation

  $$F_{s}(x)=\max \left\{x, q_{1} E F_{s-1}\left(x+R_{1}\right), q_{2} E F_{s-1}\left(x+R_{2}\right)\right\}$$

  with $R_{j}, F_{0}(x)$ appropriately defined, prove that there exists an optimal policy under which he burgles another night if and only if his wealth is less than $x^{*}=\max _{i}\left\{a_{i} q_{i} / p_{i}\right\}$.

  Suppose $q_{1}>q_{2}$ and $q_{1} a_{1}>q_{2} a_{2}$. Prove that he should never burgle in town 2 .

  [Hint: Suppose $x<x^{*}$, there are $s$ nights to go, and it has been shown that he ought not burgle in town 2 if less than $s$ nights remain. For the case $a_{2}>a_{1}$, separately consider subcases $x+2 a_{2} \geqslant x^{*}$ and $x+2 a_{2}<x^{*}$. An interchange argument may help.]

  comment

• Paper 2, Section II, $26 \mathrm{~K}$

  Optimization and Control

  Part II, 2015

  As a function of policy $\pi$ and initial state $x$, let

  $$F(\pi, x)=E_{\pi}\left[\sum_{t=0}^{\infty} \beta^{t} r\left(x_{t}, u_{t}\right) \mid x_{0}=x\right]$$

  where $\beta \geqslant 1$ and $r(x, u) \geqslant 0$ for all $x, u$. Suppose that for a specific policy $\pi$, and all $x$,

  $$F(\pi, x)=\sup _{u}\left\{r(x, u)+\beta E\left[F\left(\pi, x_{1}\right) \mid x_{0}=x, u_{0}=u\right]\right\} .$$

  Prove that $F(\pi, x) \geqslant F\left(\pi^{\prime}, x\right)$ for all $\pi^{\prime}$ and $x$.

  A gambler plays games in which he may bet 1 or 2 pounds, but no more than his present wealth. Suppose he has $x_{t}$ pounds after $t$ games. If he bets $i$ pounds then $x_{t+1}=x_{t}+i$, or $x_{t+1}=x_{t}-i$, with probabilities $p_{i}$ and $1-p_{i}$ respectively. Gambling terminates at the first $\tau$ such that $x_{\tau}=0$ or $x_{\tau}=100$. His final reward is $(9 / 8)^{\tau / 2} x_{\tau}$. Let $\pi$ be the policy of always betting 1 pound. Given $p_{1}=1 / 3$, show that $F(\pi, x) \propto x 2^{x / 2}$.

  Is $\pi$ optimal when $p_{2}=1 / 4$ ?

  comment

• Paper 4, Section II, E

  Partial Differential Equations

  Part II, 2015

  (a) Show that the Cauchy problem for $u(x, t)$ satisfying

  $$u_{t}+u=u_{x x}$$

  with initial data $u(x, 0)=u_{0}(x)$, which is a smooth $2 \pi$-periodic function of $x$, defines a strongly continuous one parameter semi-group of contractions on the Sobolev space $H_{\text {per }}^{s}$ for any $s \in\{0,1,2, \ldots\}$.

  (b) Solve the Cauchy problem for the equation

  $$u_{t t}+u_{t}+\frac{1}{4} u=u_{x x}$$

  with $u(x, 0)=u_{0}(x), u_{t}(x, 0)=u_{1}(x)$, where $u_{0}, u_{1}$ are smooth $2 \pi$-periodic functions of $x$, and show that the solution is smooth. Prove from first principles that the solution satisfies the property of finite propagation speed.

  [In this question all functions are real-valued, and

  $$H_{\text {per }}^{s}=\left\{u=\sum_{m \in \mathbb{Z}} \hat{u}(m) e^{i m x} \in L^{2}:\|u\|_{H^{s}}^{2}=\sum_{m \in \mathbb{Z}}\left(1+m^{2}\right)^{s}|\hat{u}(m)|^{2}<\infty\right\}$$

  are the Sobolev spaces of functions which are $2 \pi$-periodic in $x$, for $s=0,1,2, \ldots]$

  comment

• Paper 3, Section II, E

  Partial Differential Equations

  Part II, 2015

  (a) Show that if $f \in \mathcal{S}\left(\mathbb{R}^{n}\right)$ is a Schwartz function and $u$ is a tempered distribution which solves

  $$-\Delta u+m^{2} u=f$$

  for some constant $m \neq 0$, then there exists a number $C>0$ which depends only on $m$, such that $\|u\|_{H^{s+2}} \leqslant C\|f\|_{H^{s}}$ for any $s \geqslant 0$. Explain briefly why this inequality remains valid if $f$ is only assumed to be in $H^{s}\left(\mathbb{R}^{n}\right)$.

  Show that if $\epsilon>0$ is given then $\|v\|_{H^{1}}^{2} \leqslant \epsilon\|v\|_{H^{2}}^{2}+\frac{1}{4 \epsilon}\|v\|_{H^{0}}^{2}$ for any $v \in H^{2}\left(\mathbb{R}^{n}\right)$.

  [Hint: The inequality $a \leqslant \epsilon a^{2}+\frac{1}{4 \epsilon}$ holds for any positive $\epsilon$ and $a \in \mathbb{R} .$ ]

  Prove that if $u$ is a smooth bounded function which solves

  $$-\Delta u+m^{2} u=u^{3}+\alpha \cdot \nabla u$$

  for some constant vector $\alpha \in \mathbb{R}^{n}$ and constant $m \neq 0$, then there exists a number $C^{\prime}>0$ such that $\|u\|_{H^{2}} \leqslant C^{\prime}$ and $C^{\prime}$ depends only on $m, \alpha,\|u\|_{L^{\infty}},\|u\|_{L^{2}}$.

  [You may use the fact that, for non-negative $s$, the Sobolev space of functions

  $$\left.H^{s}\left(\mathbb{R}^{n}\right)=\left\{f \in L^{2}\left(\mathbb{R}^{n}\right):\|f\|_{H^{s}}^{2}=\int_{\mathbb{R}^{n}}\left(1+\|\xi\|^{2}\right)^{s}|\hat{f}(\xi)|^{2} d \xi<\infty\right\} .\right]$$

  (b) Let $u(x, t)$ be a smooth real-valued function, which is $2 \pi$-periodic in $x$ and satisfies the equation

  $$u_{t}=u^{2} u_{x x}+u^{3}$$

  Give a complete proof that if $u(x, 0)>0$ for all $x$ then $u(x, t)>0$ for all $x$ and $t>0$.

  comment

• Paper 2, Section II, E

  Partial Differential Equations

  Part II, 2015

  Prove that if $\phi \in C\left(\mathbb{R}^{n}\right)$ is absolutely integrable with $\int \phi(x) d x=1$, and $\phi_{\epsilon}(x)=\epsilon^{-n} \phi(x / \epsilon)$ for $\epsilon>0$, then for every Schwartz function $f \in \mathcal{S}\left(\mathbb{R}^{n}\right)$ the convolution

  $$\phi_{\epsilon} * f(x) \rightarrow f(x)$$

  uniformly in $x$ as $\epsilon \downarrow 0$.

  Show that the function $N_{\epsilon} \in C^{\infty}\left(\mathbb{R}^{3}\right)$ given by

  $$N_{\epsilon}(x)=\frac{1}{4 \pi \sqrt{|x|^{2}+\epsilon^{2}}}$$

  for $\epsilon>0$ satisfies

  $$\lim _{\epsilon \rightarrow 0} \int_{\mathbb{R}^{3}}-\Delta N_{\epsilon}(x) f(x) d x=f(0)$$

  for $f \in \mathcal{S}\left(\mathbb{R}^{n}\right)$. Hence prove that the tempered distribution determined by the function $N(x)=(4 \pi|x|)^{-1}$ is a fundamental solution of the operator $-\Delta .$

  [You may use the fact that $\int_{0}^{\infty} r^{2} /\left(1+r^{2}\right)^{5 / 2} d r=1 / 3 .$ ]

  comment

• Paper 1, Section II, E

  Partial Differential Equations

  Part II, 2015

  (a) State the Cauchy-Kovalevskaya theorem, and explain for which values of $a \in \mathbb{R}$ it implies the existence of solutions to the Cauchy problem

  $$x u_{x}+y u_{y}+a u_{z}=u, \quad u(x, y, 0)=f(x, y),$$

  where $f$ is real analytic. Using the method of characteristics, solve this problem for these values of $a$, and comment on the behaviour of the characteristics as $a$ approaches any value where the non-characteristic condition fails.

  (b) Consider the Cauchy problem

  $$u_{y}=v_{x}, \quad v_{y}=-u_{x}$$

  with initial data $u(x, 0)=f(x)$ and $v(x, 0)=0$ which are $2 \pi$-periodic in $x$. Give an example of a sequence of smooth solutions $\left(u_{n}, v_{n}\right)$ which are also $2 \pi$-periodic in $x$ whose corresponding initial data $u_{n}(x, 0)=f_{n}(x)$ and $v_{n}(x, 0)=0$ are such that $\int_{0}^{2 \pi}\left|f_{n}(x)\right|^{2} d x \rightarrow 0$ while $\int_{0}^{2 \pi}\left|u_{n}(x, y)\right|^{2} d x \rightarrow \infty$ for non-zero $y$ as $n \rightarrow \infty$

  Comment on the significance of this in relation to the concept of well-posedness.

  comment

• Paper 4, Section II, A

  Principles of Quantum Mechanics

  Part II, 2015

  The Hamiltonian for a quantum system in the Schrödinger picture is $H_{0}+\lambda V(t)$, where $H_{0}$ is independent of time and the parameter $\lambda$ is small. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.

  Suppose that $|\chi\rangle$ and $|\phi\rangle$ are eigenstates of $H_{0}$ with distinct eigenvalues $E$ and $E^{\prime}$, respectively. Show that if the system is in state $|\chi\rangle$ at time zero then the probability of measuring it to be in state $|\phi\rangle$ at time $t$ is

  $$\frac{\lambda^{2}}{\hbar^{2}}\left|\int_{0}^{t} d t^{\prime}\left\langle\phi\left|V\left(t^{\prime}\right)\right| \chi\right\rangle e^{i\left(E^{\prime}-E\right) t^{\prime} / \hbar}\right|^{2}+O\left(\lambda^{3}\right)$$

  Let $H_{0}$ be the Hamiltonian for an isotropic three-dimensional harmonic oscillator of mass $m$ and frequency $\omega$, with $\chi(r)$ being the ground state wavefunction (where $r=|\mathbf{x}|$ ) and $\phi_{i}(\mathbf{x})=(2 m \omega / \hbar)^{1 / 2} x_{i} \chi(r)$ being wavefunctions for the states at the first excited energy level $(i=1,2,3)$. The oscillator is in its ground state at $t=0$ when a perturbation

  $$\lambda V(t)=\lambda \hat{x}_{3} e^{-\mu t}$$

  is applied, with $\mu>0$, and $H_{0}$ is then measured after a very large time has elapsed. Show that to first order in perturbation theory the oscillator will be found in one particular state at the first excited energy level with probability

  $$\frac{\lambda^{2}}{2 \hbar m \omega\left(\mu^{2}+\omega^{2}\right)},$$

  but that the probability that it will be found in either of the other excited states is zero (to this order).

  $\left[\right.$ You may use the fact that $\left.4 \pi \int_{0}^{\infty} r^{4}|\chi(r)|^{2} d r=\frac{3 \hbar}{2 m \omega} .\right]$

  comment

• Paper 3, Section II, A

  Principles of Quantum Mechanics

  Part II, 2015

  Let $|j, m\rangle$ denote the normalised joint eigenstates of $\mathbf{J}^{2}$ and $J_{3}$, where $\mathbf{J}$ is the angular momentum operator for a quantum system. State clearly the possible values of the quantum numbers $j$ and $m$ and write down the corresponding eigenvalues in units with $\hbar=1$.

  Consider two quantum systems with angular momentum states $\left|\frac{1}{2}, r\right\rangle$ and $|j, m\rangle$. The eigenstates corresponding to their combined angular momentum can be written as

  $$|J, M\rangle=\sum_{r, m} C_{r m}^{J M}\left|\frac{1}{2}, r\right\rangle|j, m\rangle,$$

  where $C_{r m}^{J M}$ are Clebsch-Gordan coefficients for addition of angular momenta $\frac{1}{2}$ and $j$. What are the possible values of $J$ and what is a necessary condition relating $r, m$ and $M$ in order that $C_{r m}^{J M} \neq 0$ ?

  Calculate the values of $C_{r m}^{J M}$ for $j=2$ and for all $M \geqslant \frac{3}{2}$. Use the sign convention that $C_{r m}^{J J}>0$ when $m$ takes its maximum value.

  A particle $X$ with spin $\frac{3}{2}$ and intrinsic parity $\eta_{X}$ is at rest. It decays into two particles $A$ and $B$ with spin $\frac{1}{2}$ and spin 0 , respectively. Both $A$ and $B$ have intrinsic parity $-1$. The relative orbital angular momentum quantum number for the two particle system is $\ell$. What are the possible values of $\ell$ for the cases $\eta_{X}=+1$ and $\eta_{X}=-1$ ?

  Suppose particle $X$ is prepared in the state $\left|\frac{3}{2}, \frac{3}{2}\right\rangle$ before it decays. Calculate the probability $P$ for particle $A$ to be found in the state $\left|\frac{1}{2}, \frac{1}{2}\right\rangle$, given that $\eta_{X}=+1$.

  What is the probability $P$ if instead $\eta_{X}=-1$ ?

  [Units with $\hbar=1$ should be used throughout. You may also use without proof

  $$\left.J_{-}|j, m\rangle=\sqrt{(j+m)(j-m+1)}|j, m-1\rangle .\right]$$

  comment

• Paper 2, Section II, A

  Principles of Quantum Mechanics

  Part II, 2015

  Express the spin operator $\mathbf{S}$ for a particle of spin $\frac{1}{2}$ in terms of the Pauli matrices $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ where

  $$\sigma_{1}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  Show that $(\mathbf{n} \cdot \boldsymbol{\sigma})^{2}=\mathbb{I}$ for any unit vector $\mathbf{n}$ and deduce that

  $$e^{-i \theta \mathbf{n} \cdot \mathbf{S} / \hbar}=\mathbb{I} \cos (\theta / 2)-i(\mathbf{n} \cdot \boldsymbol{\sigma}) \sin (\theta / 2) .$$

  The space of states $V$ for a particle of spin $\frac{1}{2}$ has basis states $|\uparrow\rangle,|\downarrow\rangle$ which are eigenstates of $S_{3}$ with eigenvalues $\frac{1}{2} \hbar$ and $-\frac{1}{2} \hbar$ respectively. If the Hamiltonian for the particle is $H=\frac{1}{2} \alpha \hbar \sigma_{1}$, find

  $$e^{-i t H / \hbar}|\uparrow\rangle \quad \text { and } \quad e^{-i t H / \hbar}|\downarrow\rangle$$

  as linear combinations of the basis states.

  The space of states for a system of two spin $\frac{1}{2}$ particles is $V \otimes V$. Write down explicit expressions for the joint eigenstates of $\mathbf{J}^{2}$ and $J_{3}$, where $\mathbf{J}$ is the sum of the spin operators for the particles.

  Suppose that the two-particle system has Hamiltonian $H=\frac{1}{2} \lambda \hbar\left(\sigma_{1} \otimes \mathbb{I}-\mathbb{I} \otimes \sigma_{1}\right)$ and that at time $t=0$ the system is in the state with $J_{3}$ eigenvalue $\hbar$. Calculate the probability that at time $t>0$ the system will be measured to be in the state with $\mathbf{J}^{2}$ eigenvalue zero.

  comment

• Paper 3, Section II, A

  Applications of Quantum Mechanics

  Part II, 2015

  A particle of mass $m$ and energy $E=-\hbar^{2} \kappa^{2} / 2 m<0$ moves in one dimension subject to a periodic potential

  $$V(x)=-\frac{\hbar^{2} \lambda}{m} \sum_{\ell=-\infty}^{\infty} \delta(x-\ell a) \quad \text { with } \quad \lambda>0 .$$

  Determine the corresponding Floquet matrix $\mathcal{M}$. [You may assume without proof that for the Schrödinger equation with potential $\alpha \delta(x)$ the wavefunction $\psi(x)$ is continuous at $x=0$ and satisfies $\left.\psi^{\prime}(0+)-\psi^{\prime}(0-)=\left(2 m \alpha / \hbar^{2}\right) \psi(0) .\right]$

  Explain briefly, with reference to Bloch's theorem, how restrictions on the energy of a Bloch state can be derived from $\mathcal{M}$. Deduce that for the potential $V(x)$ above, $\kappa$ is confined to a range whose boundary values are determined by

  $$\tanh \left(\frac{\kappa a}{2}\right)=\frac{\kappa}{\lambda} \quad \text { and } \quad \operatorname{coth}\left(\frac{\kappa a}{2}\right)=\frac{\kappa}{\lambda} .$$

  Sketch the left-hand and right-hand sides of each of these equations as functions of $y=\kappa a / 2$. Hence show that there is exactly one allowed band of negative energies with either (i) $E_{-} \leqslant E<0$ or (ii) $E_{-} \leqslant E \leqslant E_{+}<0$ and determine the values of $\lambda a$ for which each of these cases arise. [You should not attempt to evaluate the constants $E_{\pm} .$]

  Comment briefly on the limit $a \rightarrow \infty$ with $\lambda$ fixed.

  comment

• Paper 1, Section II, A

  Principles of Quantum Mechanics

  Part II, 2015

  If $A$ and $B$ are operators which each commute with their commutator $[A, B]$, show that

  $$F(\lambda)=e^{\lambda A} e^{\lambda B} e^{-\lambda(A+B)} \quad \text { satisfies } \quad F^{\prime}(\lambda)=\lambda[A, B] F(\lambda)$$

  By solving this differential equation for $F(\lambda)$, deduce that

  $$e^{A} e^{B}=e^{\frac{1}{2}[A, B]} e^{A+B}$$

  The annihilation and creation operators for a harmonic oscillator of mass $m$ and frequency $\omega$ are defined by

  $$a=\sqrt{\frac{m \omega}{2 \hbar}}\left(\hat{x}+\frac{i}{m \omega} \hat{p}\right), \quad a^{\dagger}=\sqrt{\frac{m \omega}{2 \hbar}}\left(\hat{x}-\frac{i}{m \omega} \hat{p}\right)$$

  Write down an expression for the general normalised eigenstate $|n\rangle(n=0,1,2, \ldots)$ of the oscillator Hamiltonian $H$ in terms of the ground state $|0\rangle$. What is the energy eigenvalue $E_{n}$ of the state $|n\rangle ?$

  Suppose the oscillator is now subject to a small perturbation so that it is described by the modified Hamiltonian $H+\varepsilon V(\hat{x})$ with $V(\hat{x})=\cos (\mu \hat{x})$. Show that

  $$V(\hat{x})=\frac{1}{2} e^{-\gamma^{2} / 2}\left(e^{i \gamma a^{\dagger}} e^{i \gamma a}+e^{-i \gamma a^{\dagger}} e^{-i \gamma a}\right)$$

  where $\gamma$ is a constant, to be determined. Hence show that to $O\left(\varepsilon^{2}\right)$ the shift in the ground state energy as a result of the perturbation is

  $$\varepsilon e^{-\mu^{2} \hbar / 4 m \omega}-\varepsilon^{2} e^{-\mu^{2} \hbar / 2 m \omega} \frac{1}{\hbar \omega} \sum_{p=1}^{\infty} \frac{1}{(2 p) ! 2 p}\left(\frac{\mu^{2} \hbar}{2 m \omega}\right)^{2 p} .$$

  [Standard results of perturbation theory may be quoted without proof.]

  comment

• Paper 4, Section II, $\mathbf{2 4 J}$

  Principles of Statistics

  Part II, 2015

  Given independent and identically distributed observations $X_{1}, \ldots, X_{n}$ with finite mean $E\left(X_{1}\right)=\mu$ and variance $\operatorname{Var}\left(X_{1}\right)=\sigma^{2}$, explain the notion of a bootstrap sample $X_{1}^{b}, \ldots, X_{n}^{b}$, and discuss how you can use it to construct a confidence interval $C_{n}$ for $\mu$.

  Suppose you can operate a random number generator that can simulate independent uniform random variables $U_{1}, \ldots, U_{n}$ on $[0,1]$. How can you use such a random number generator to simulate a bootstrap sample?

  Suppose that $\left(F_{n}: n \in \mathbb{N}\right)$ and $F$ are cumulative probability distribution functions defined on the real line, that $F_{n}(t) \rightarrow F(t)$ as $n \rightarrow \infty$ for every $t \in \mathbb{R}$, and that $F$ is continuous on $\mathbb{R}$. Show that, as $n \rightarrow \infty$,

  $$\sup _{t \in \mathbb{R}}\left|F_{n}(t)-F(t)\right| \rightarrow 0 .$$

  State (without proof) the theorem about the consistency of the bootstrap of the mean, and use it to give an asymptotic justification of the confidence interval $C_{n}$. That is, prove that as $n \rightarrow \infty, P^{\mathbb{N}}\left(\mu \in C_{n}\right) \rightarrow 1-\alpha$ where $P^{\mathbb{N}}$ is the joint distribution of $X_{1}, X_{2}, \ldots$

  [You may use standard facts of stochastic convergence and the Central Limit Theorem without proof.]

  comment

• Paper 3, Section II, J

  Principles of Statistics

  Part II, 2015

  Define what it means for an estimator $\hat{\theta}$ of an unknown parameter $\theta$ to be consistent.

  Let $S_{n}$ be a sequence of random real-valued continuous functions defined on $\mathbb{R}$ such that, as $n \rightarrow \infty, S_{n}(\theta)$ converges to $S(\theta)$ in probability for every $\theta \in \mathbb{R}$, where $S: \mathbb{R} \rightarrow \mathbb{R}$ is non-random. Suppose that for some $\theta_{0} \in \mathbb{R}$ and every $\varepsilon>0$ we have

  $$S\left(\theta_{0}-\varepsilon\right)<0<S\left(\theta_{0}+\varepsilon\right),$$

  and that $S_{n}$ has exactly one zero $\hat{\theta}_{n}$ for every $n \in \mathbb{N}$. Show that $\hat{\theta}_{n} \rightarrow \theta_{0}$ as $n \rightarrow \infty$, and deduce from this that the maximum likelihood estimator (MLE) based on observations $X_{1}, \ldots, X_{n}$ from a $N(\theta, 1), \theta \in \mathbb{R}$ model is consistent.

  Now consider independent observations $\mathbf{X}_{1}, \ldots, \mathbf{X}_{n}$ of bivariate normal random vectors

  $$\mathbf{X}_{i}=\left(X_{1 i}, X_{2 i}\right)^{T} \sim N_{2}\left[\left(\mu_{i}, \mu_{i}\right)^{T}, \sigma^{2} I_{2}\right], \quad i=1, \ldots, n,$$

  where $\mu_{i} \in \mathbb{R}, \sigma>0$ and $I_{2}$ is the $2 \times 2$ identity matrix. Find the MLE $\hat{\mu}=\left(\hat{\mu}_{1}, \ldots, \hat{\mu}_{n}\right)^{T}$ of $\mu=\left(\mu_{1}, \ldots, \mu_{n}\right)^{T}$ and show that the MLE of $\sigma^{2}$ equals

  $$\hat{\sigma}^{2}=\frac{1}{n} \sum_{i=1}^{n} s_{i}^{2}, \quad s_{i}^{2}=\frac{1}{2}\left[\left(X_{1 i}-\hat{\mu}_{i}\right)^{2}+\left(X_{2 i}-\hat{\mu}_{i}\right)^{2}\right]$$

  Show that $\hat{\sigma}^{2}$ is not consistent for estimating $\sigma^{2}$. Explain briefly why the MLE fails in this model.

  [You may use the Law of Large Numbers without proof.]

  comment

• Paper 2, Section II, J

  Principles of Statistics

  Part II, 2015

  Consider a random variable $X$ arising from the binomial distribution $\operatorname{Bin}(n, \theta)$, $\theta \in \Theta=[0,1]$. Find the maximum likelihood estimator $\hat{\theta}_{M L E}$ and the Fisher information $I(\theta)$ for $\theta \in \Theta$.

  Now consider the following priors on $\Theta$ :

  (i) a uniform $U([0,1])$ prior on $[0,1]$,

  (ii) a prior with density $\pi(\theta)$ proportional to $\sqrt{I(\theta)}$,

  (iii) a $\operatorname{Beta}(\sqrt{n} / 2, \sqrt{n} / 2)$ prior.

  Find the means $E[\theta \mid X]$ and modes $m_{\theta} \mid X$ of the posterior distributions corresponding to the prior distributions (i)-(iii). Which of these posterior decision rules coincide with $\hat{\theta}_{M L E}$ ? Which one is minimax for quadratic risk? Justify your answers.

  [You may use the following properties of the $\operatorname{Beta}(a, b)(a>0, b>0)$ distribution. Its density $f(x ; a, b), x \in[0,1]$, is proportional to $x^{a-1}(1-x)^{b-1}$, its mean is equal to $a /(a+b)$, and its mode is equal to

  $$\frac{\max (a-1,0)}{\max (a, 1)+\max (b, 1)-2}$$

  provided either $a>1$ or $b>1$.

  You may further use the fact that a unique Bayes rule of constant risk is a unique minimax rule for that risk.]

  comment

• Paper 1, Section II, J

  Principles of Statistics

  Part II, 2015

  Consider a normally distributed random vector $X \in \mathbb{R}^{p}$ modelled as $X \sim N\left(\theta, I_{p}\right)$ where $\theta \in \mathbb{R}^{p}, I_{p}$ is the $p \times p$ identity matrix, and where $p \geqslant 3$. Define the Stein estimator $\hat{\theta}_{S T E I N}$ of $\theta$.

  Prove that $\hat{\theta}_{S T E I N}$ dominates the estimator $\tilde{\theta}=X$ for the risk function induced by quadratic loss

  $$\ell(a, \theta)=\sum_{i=1}^{p}\left(a_{i}-\theta_{i}\right)^{2}, \quad a \in \mathbb{R}^{p}$$

  Show however that the worst case risks coincide, that is, show that

  $$\sup _{\theta \in \mathbb{R}^{p}} E_{\theta} \ell(X, \theta)=\sup _{\theta \in \mathbb{R}^{p}} E_{\theta} \ell\left(\hat{\theta}_{S T E I N}, \theta\right)$$

  [You may use Stein's lemma without proof, provided it is clearly stated.]

  comment

• Paper 4, Section II, J

  Probability and Measure

  Part II, 2015

  (a) State Fatou's lemma.

  (b) Let $X$ be a random variable on $\mathbb{R}^{d}$ and let $\left(X_{k}\right)_{k=1}^{\infty}$ be a sequence of random variables on $\mathbb{R}^{d}$. What does it mean to say that $X_{k} \rightarrow X$ weakly?

  State and prove the Central Limit Theorem for i.i.d. real-valued random variables. [You may use auxiliary theorems proved in the course provided these are clearly stated.]

  (c) Let $X$ be a real-valued random variable with characteristic function $\varphi$. Let $\left(h_{n}\right)_{n=1}^{\infty}$ be a sequence of real numbers with $h_{n} \neq 0$ and $h_{n} \rightarrow 0$. Prove that if we have

  $$\liminf _{n \rightarrow \infty} \frac{2 \varphi(0)-\varphi\left(-h_{n}\right)-\varphi\left(h_{n}\right)}{h_{n}^{2}}<\infty$$

  then $\mathbb{E}\left[X^{2}\right]<\infty$

  comment

• Paper 3 , Section II, J

  Probability and Measure

  Part II, 2015

  (a) Let $(E, \mathcal{E}, \mu)$ be a measure space. What does it mean to say that $T: E \rightarrow E$ is a measure-preserving transformation? What does it mean to say that a set $A \in \mathcal{E}$ is invariant under $T$ ? Show that the class of invariant sets forms a $\sigma$-algebra.

  (b) Take $E$ to be $[0,1)$ with Lebesgue measure on its Borel $\sigma$-algebra. Show that the baker's map $T:[0,1) \rightarrow[0,1)$ defined by

  $$T(x)=2 x-\lfloor 2 x\rfloor$$

  is measure-preserving.

  (c) Describe in detail the construction of the canonical model for sequences of independent random variables having a given distribution $m$.

  Define the Bernoulli shift map and prove it is a measure-preserving ergodic transformation.

  [You may use without proof other results concerning sequences of independent random variables proved in the course, provided you state these clearly.]

  comment

• Paper 2, Section II, J

  Probability and Measure

  Part II, 2015

  (a) Let $(E, \mathcal{E}, \mu)$ be a measure space, and let $1 \leqslant p<\infty$. What does it mean to say that $f$ belongs to $L^{p}(E, \mathcal{E}, \mu)$ ?

  (b) State Hölder's inequality.

  (c) Consider the measure space of the unit interval endowed with Lebesgue measure. Suppose $f \in L^{2}(0,1)$ and let $0<\alpha<1 / 2$.

  (i) Show that for all $x \in \mathbb{R}$,

  $$\int_{0}^{1}|f(y)||x-y|^{-\alpha} d y<\infty$$

  (ii) For $x \in \mathbb{R}$, define

  $$g(x)=\int_{0}^{1} f(y)|x-y|^{-\alpha} d y$$

  Show that for $x \in \mathbb{R}$ fixed, the function $g$ satisfies

  $$|g(x+h)-g(x)| \leqslant\|f\|_{2} \cdot(I(h))^{1 / 2},$$

  where

  $$I(h)=\int_{0}^{1}\left(|x+h-y|^{-\alpha}-|x-y|^{-\alpha}\right)^{2} d y .$$

  (iii) Prove that $g$ is a continuous function. [Hint: You may find it helpful to split the integral defining $I(h)$ into several parts.]

  comment

• Paper 1, Section II, J

  Probability and Measure

  Part II, 2015

  (a) Define the following concepts: a $\pi$-system, a $d$-system and a $\sigma$-algebra.

  (b) State the Dominated Convergence Theorem.

  (c) Does the set function

  $$\mu(A)= \begin{cases}0 & \text { for } A \text { bounded } \\ 1 & \text { for } A \text { unbounded }\end{cases}$$

  furnish an example of a Borel measure?

  (d) Suppose $g:[0,1] \rightarrow[0,1]$ is a measurable function. Let $f:[0,1] \rightarrow \mathbb{R}$ be continuous with $f(0) \leqslant f(1)$. Show that the limit

  $$\lim _{n \rightarrow \infty} \int_{0}^{1} f\left(g(x)^{n}\right) d x$$

  exists and lies in the interval $[f(0), f(1)]$

  comment

• Paper 4, Section II, F

  Representation Theory

  Part II, 2015

  (a) Let $S^{1}$ be the circle group. Assuming any required facts about continuous functions from real analysis, show that every 1-dimensional continuous representation of $S^{1}$ is of the form

  $$z \mapsto z^{n}$$

  for some $n \in \mathbb{Z}$.

  (b) Let $G=S U(2)$, and let $\rho_{V}$ be a continuous representation of $G$ on a finitedimensional vector space $V$.

  (i) Define the character $\chi_{V}$ of $\rho_{V}$, and show that $\chi_{V} \in \mathbb{N}\left[z, z^{-1}\right]$.

  (ii) Show that $\chi_{V}(z)=\chi_{V}\left(z^{-1}\right)$.

  (iii) Let $V$ be the irreducible 4-dimensional representation of $G$. Decompose $V \otimes V$ into irreducible representations. Hence decompose the exterior square $\Lambda^{2} V$ into irreducible representations.

  comment

• Paper 4, Section II, K

  Applied Probability

  Part II, 2015

  (i) Let $X$ be a Markov chain on $S$ and $A \subset S$. Let $T_{A}$ be the hitting time of $A$ and $\tau_{y}$ denote the total time spent at $y \in S$ by the chain before hitting $A$. Show that if $h(x)=\mathbb{P}_{x}\left(T_{A}<\infty\right)$, then $\mathbb{E}_{x}\left[\tau_{y} \mid T_{A}<\infty\right]=[h(y) / h(x)] \mathbb{E}_{x}\left(\tau_{y}\right) .$

  (ii) Define the Moran model and show that if $X_{t}$ is the number of individuals carrying allele $a$ at time $t \geqslant 0$ and $\tau$ is the fixation time of allele $a$, then

  $$\mathbb{P}\left(X_{\tau}=N \mid X_{0}=i\right)=\frac{i}{N}$$

  Show that conditionally on fixation of an allele $a$ being present initially in $i$ individuals,

  $$\mathbb{E}[\tau \mid \text { fixation }]=N-i+\frac{N-i}{i} \sum_{j=1}^{i-1} \frac{j}{N-j}$$

  comment

• Paper 3, Section II, F

  Representation Theory

  Part II, 2015

  (a) State Mackey's theorem, defining carefully all the terms used in the statement.

  (b) Let $G$ be a finite group and suppose that $G$ acts on the set $\Omega$.

  If $n \in \mathbb{N}$, we say that the action of $G$ on $\Omega$ is $n$-transitive if $\Omega$ has at least $n$ elements and for every pair of $n$-tuples $\left(a_{1}, \ldots, a_{n}\right)$ and $\left(b_{1}, \ldots, b_{n}\right)$ such that the $a_{i}$ are distinct elements of $\Omega$ and the $b_{i}$ are distinct elements of $\Omega$, there exists $g \in G$ with $g a_{i}=b_{i}$ for every $i$.

  (i) Let $\Omega$ have at least $n$ elements, where $n \geqslant 1$ and let $\omega \in \Omega$. Show that $G$ acts $n$-transitively on $\Omega$ if and only if $G$ acts transitively on $\Omega$ and the stabiliser $G_{\omega}$ acts $(n-1)$-transitively on $\Omega \backslash\{\omega\}$.

  (ii) Show that the permutation module $\mathbb{C} \Omega$ can be decomposed as

  $$\mathbb{C} \Omega=\mathbb{C}_{G} \oplus V,$$

  where $\mathbb{C}_{G}$ is the trivial module and $V$ is some $\mathbb{C} G$-module.

  (iii) Assume that $|\Omega| \geqslant 2$, so that $V \neq 0$. Prove that $V$ is irreducible if and only if $G$ acts 2-transitively on $\Omega$. In that case show also that $V$ is not the trivial representation. [Hint: Pick any orbit of $G$ on $\Omega$; it is isomorphic as a $G$-set to $G / H$ for some subgroup $H \leqslant G$. Consider the induced character $\left.\operatorname{Ind}_{H}^{G} 1_{H} \cdot\right]$

  comment

• Paper 2, Section II, $15 F$

  Representation Theory

  Part II, 2015

  Let $G$ be a finite group. Suppose that $\rho: G \rightarrow G \mathrm{G}(V)$ is a finite-dimensional complex representation of dimension $d$. Let $n \in \mathbb{N}$ be arbitrary.

  (i) Define the $n$th symmetric power $S^{n} V$ and the $n$th exterior power $\Lambda^{n} V$ and write down their respective dimensions.

  Let $g \in G$ and let $\lambda_{1}, \ldots, \lambda_{d}$ be the eigenvalues of $g$ on $V$. What are the eigenvalues of $g$ on $S^{n} V$ and on $\Lambda^{n} V$ ?

  (ii) Let $X$ be an indeterminate. For any $g \in G$, define the characteristic polynomial $Q=Q(g, X)$ of $g$ on $V$ by $Q(g, X):=\operatorname{det}(g-X I)$. What is the relationship between the coefficients of $Q$ and the character $\chi_{\Lambda^{n}} V$ of the exterior power?

  Find a relation between the character $\chi_{S^{n}} V$ of the symmetric power and the polynomial $Q$.

  comment

• Paper 1, Section II, F

  Representation Theory

  Part II, 2015

  (a) Let $G$ be a finite group and let $\rho: G \rightarrow \mathrm{GL}_{2}(\mathbb{C})$ be a representation of $G$. Suppose that there are elements $g, h$ in $G$ such that the matrices $\rho(g)$ and $\rho(h)$ do not commute. Use Maschke's theorem to prove that $\rho$ is irreducible.

  (b) Let $n$ be a positive integer. You are given that the dicyclic group

  $$G_{4 n}=\left\langle a, b: a^{2 n}=1, a^{n}=b^{2}, b^{-1} a b=a^{-1}\right\rangle$$

  has order $4 n$.

  (i) Show that if $\epsilon$ is any $(2 n)$ th root of unity in $\mathbb{C}$, then there is a representation of $G_{4 n}$ over $\mathbb{C}$ which sends

  $$a \mapsto\left(\begin{array}{cc} \epsilon & 0 \\ 0 & \epsilon^{-1} \end{array}\right), \quad b \mapsto\left(\begin{array}{cc} 0 & 1 \\ \epsilon^{n} & 0 \end{array}\right)$$

  (ii) Find all the irreducible representations of $G_{4 n}$.

  (iii) Find the character table of $G_{4 n}$.

  [Hint: You may find it helpful to consider the cases $n$ odd and $n$ even separately.]

  comment

• Paper 3, Section II, F

  Riemann Surfaces

  Part II, 2015

  Let $\wp(z)$ denote the Weierstrass $\wp$-function with respect to a lattice $\Lambda \subset \mathbb{C}$ and let $f$ be an even elliptic function with periods $\Lambda$. Prove that there exists a rational function $Q$ such that $f(z)=Q(\wp(z))$. If we write $Q(w)=p(w) / q(w)$ where $p$ and $q$ are coprime polynomials, find the degree of $f$ in terms of the degrees of the polynomials $p$ and $q$. Describe all even elliptic functions of degree two. Justify your answers. [You may use standard properties of the Weierstrass $\wp$-function.]

  comment

• Paper 2, Section II, F

  Riemann Surfaces

  Part II, 2015

  Let $G$ be a domain in $\mathbb{C}$. Define the germ of a function element $(f, D)$ at $z \in D$. Let $\mathcal{G}$ be the set of all germs of function elements in $G$. Define the topology on $\mathcal{G}$. Show it is a topology, and that it is Hausdorff. Define the complex structure on $\mathcal{G}$, and show that there is a natural projection map $\pi: \mathcal{G} \rightarrow G$ which is an analytic covering map on each connected component of $\mathcal{G}$.

  Given a complete analytic function $\mathcal{F}$ on $G$, describe how it determines a connected component $\mathcal{G}_{\mathcal{F}}$ of $\mathcal{G}$. [You may assume that a function element $(g, E)$ is an analytic continuation of a function element $(f, D)$ along a path $\gamma:[0,1] \rightarrow G$ if and only if there is a lift of $\gamma$ to $\mathcal{G}$ starting at the germ of $(f, D)$ at $\gamma(0)$ and ending at the germ of $(g, E)$ at $\gamma(1)$.]

  In each of the following cases, give an example of a domain $G$ in $\mathbb{C}$ and a complete analytic function $\mathcal{F}$ such that:

  (i) $\pi: \mathcal{G}_{\mathcal{F}} \rightarrow G$ is regular but not bijective;

  (ii) $\pi: \mathcal{G}_{\mathcal{F}} \rightarrow G$ is surjective but not regular.

  comment

• Paper 1, Section II, F

  Riemann Surfaces

  Part II, 2015

  Let $f: R \rightarrow S$ be a non-constant holomorphic map between compact connected Riemann surfaces and let $B \subset S$ denote the set of branch points. Show that the map $f: R \backslash f^{-1}(B) \rightarrow S \backslash B$ is a regular covering map.

  Given $w \in S \backslash B$ and a closed curve $\gamma$ in $S \backslash B$ with initial and final point $w$, explain how this defines a permutation of the (finite) set $f^{-1}(w)$. Show that the group $H$ obtained from all such closed curves is a transitive subgroup of the full symmetric group of the fibre $f^{-1}(w)$.

  Find the group $H$ for $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ where $f(z)=z^{3} /\left(1-z^{2}\right)$.

  comment

• Paper 4, Section I, J

  Statistical Modelling

  Part II, 2015

  Data on 173 nesting female horseshoe crabs record for each crab its colour as one of 4 factors (simply labelled $1, \ldots, 4$ ), its width (in $\mathrm{cm}$ ) and the presence of male crabs nearby (a 1 indicating presence). The data are collected into the $\mathrm{R}$ data frame crabs and the first few lines are displayed below.

  

  Describe the model being fitted by the $\mathrm{R}$ command below.

  $>$ fit1 <- glm(males colour + width, family = binomial, data=crabs)

  The following (abbreviated) output is obtained from the summary command.

  

  Write out the calculation for an approximate $95 \%$ confidence interval for the coefficient for width. Describe the calculation you would perform to obtain an estimate of the probability that a female crab of colour 3 and with a width of $20 \mathrm{~cm}$ has males nearby. [You need not actually compute the end points of the confidence interval or the estimate of the probability above, but merely show the calculations that would need to be performed in order to arrive at them.]

  comment

• Paper 3, Section I, J

  Statistical Modelling

  Part II, 2015

  Data are available on the number of counts (atomic disintegration events that take place within a radiation source) recorded with a Geiger counter at a nuclear plant. The counts were registered at each second over a 30 second period for a short-lived, man-made radioactive compound. The first few rows of the dataset are displayed below.

  

  Describe the model being fitted with the following $\mathrm{R}$ command.

  $>$ fit $1<-\operatorname{lm}($ Counts $~$Time, data=geiger)

  Below is a plot against time of the residuals from the model fitted above.

  

  Referring to the plot, suggest how the model could be improved, and write out the $R$ code for fitting this new model. Briefly describe how one could test in $R$ whether the new model is to be preferred over the old model.

  comment

• Paper 2, Section I, J

  Statistical Modelling

  Part II, 2015

  Let $Y_{1}, \ldots, Y_{n}$ be independent Poisson random variables with means $\mu_{1}, \ldots, \mu_{n}$, where $\log \left(\mu_{i}\right)=\beta x_{i}$ for some known constants $x_{i} \in \mathbb{R}$ and an unknown parameter $\beta$. Find the log-likelihood for $\beta$.

  By first computing the first and second derivatives of the log-likelihood for $\beta$, describe the algorithm you would use to find the maximum likelihood estimator $\hat{\beta}$. $[$ Hint: Recall that if $Z \sim \operatorname{Pois}(\mu)$ then

  $$\mathbb{P}(Z=k)=\frac{\mu^{k} e^{-\mu}}{k !}$$

  for $k \in\{0,1,2, \ldots\}$.]

  comment

• Paper 1, Section I, J

  Statistical Modelling

  Part II, 2015

  The outputs $Y_{1}, \ldots, Y_{n}$ of a particular process are positive and are believed to be related to $p$-vectors of covariates $x_{1}, \ldots, x_{n}$ according to the following model

  $$\log \left(Y_{i}\right)=\mu+x_{i}^{T} \beta+\varepsilon_{i}$$

  In this model $\varepsilon_{i}$ are i.i.d. $N\left(0, \sigma^{2}\right)$ random variables where $\sigma>0$ is known. It is not possible to measure the output directly, but we can detect whether the output is greater than or less than or equal to a certain known value $c>0$. If

  $$Z_{i}= \begin{cases}1 & \text { if } Y_{i}>c \\ 0 & \text { if } Y_{i} \leqslant c\end{cases}$$

  show that a probit regression model can be used for the data $\left(Z_{i}, x_{i}\right), i=1, \ldots, n$.

  How can we recover $\mu$ and $\beta$ from the parameters of the probit regression model?

  comment

• Paper 3, Section II, K

  Applied Probability

  Part II, 2015

  (i) Let $X$ be a Poisson process of parameter $\lambda$. Let $Y$ be obtained by taking each point of $X$ and, independently of the other points, keeping it with probability $p$. Show that $Y$ is another Poisson process and find its intensity. Show that for every fixed $t$ the random variables $Y_{t}$ and $X_{t}-Y_{t}$ are independent.

  (ii) Suppose we have $n$ bins, and balls arrive according to a Poisson process of rate 1 . Upon arrival we choose a bin uniformly at random and place the ball in it. We let $M_{n}$ be the maximum number of balls in any bin at time $n$. Show that

  $$\mathbb{P}\left(M_{n} \geqslant(1+\epsilon) \frac{\log n}{\log \log n}\right) \rightarrow 0 \quad \text { as } n \rightarrow \infty$$

  [You may use the fact that if $\xi$ is a Poisson random variable of mean 1 , then

  $$\mathbb{P}(\xi \geqslant x) \leqslant \exp (x-x \log x) .]$$

  comment

• Paper 4, Section II, J

  Statistical Modelling

  Part II, 2015

  Consider the normal linear model where the $n$-vector of responses $Y$ satisfies $Y=X \beta+\varepsilon$ with $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$. Here $X$ is an $n \times p$ matrix of predictors with full column rank where $p \geqslant 3$ and $\beta \in \mathbb{R}^{p}$ is an unknown vector of regression coefficients. For $j \in\{1, \ldots, p\}$, denote the $j$ th column of $X$ by $X_{j}$, and let $X_{-j}$ be $X$ with its $j$ th column removed. Suppose $X_{1}=1_{n}$ where $1_{n}$ is an $n$-vector of 1 's. Denote the maximum likelihood estimate of $\beta$ by $\beta$. Write down the formula for $\hat{\beta}_{j}$ involving $P_{-j}$, the orthogonal projection onto the column space of $X_{-j}$.

  Consider $j, k \in\{2, \ldots, p\}$ with $j<k$. By thinking about the orthogonal projection of $X_{j}$ onto $X_{k}$, show that

  $$\operatorname{var}\left(\hat{\beta}_{j}\right) \geqslant \frac{\sigma^{2}}{\left\|X_{j}\right\|^{2}}\left(1-\left(\frac{X_{k}^{T} X_{j}}{\left\|X_{k}\right\|\left\|X_{j}\right\|}\right)^{2}\right)^{-1}$$

  [You may use standard facts about orthogonal projections including the fact that if $V$ and $W$ are subspaces of $\mathbb{R}^{n}$ with $V$ a subspace of $W$ and $\Pi_{V}$ and $\Pi_{W}$ denote orthogonal projections onto $V$ and $W$ respectively, then for all $v \in \mathbb{R}^{n},\left\|\Pi_{W} v\right\|^{2} \geqslant\left\|\Pi_{V} v\right\|^{2}$.]

  By considering the fitted values $X \hat{\beta}$, explain why if, for any $j \geqslant 2$, a constant is added to each entry in the $j$ th column of $X$, then $\hat{\beta}_{j}$ will remain unchanged. Let $\bar{X}_{j}=\sum_{i=1}^{n} X_{i j} / n$. Why is (*) also true when all instances of $X_{j}$ and $X_{k}$ are replaced by $X_{j}-\bar{X}_{j} 1_{n}$ and $X_{k}-\bar{X}_{k} 1_{n}$ respectively?

  The marks from mid-year statistics and mathematics tests and an end-of-year statistics exam are recorded for 100 secondary school students. The first few lines of the data are given below.

  

  The following abbreviated output is obtained:

  

  What are the hypothesis tests corresponding to the final column of the coefficients table? What is the hypothesis test corresponding to the final line of the output? Interpret the results when testing at the $5 \%$ level.

  How does the following sample correlation matrix for the data help to explain the relative sizes of some of the $p$-values?

  

  comment

• Paper 1, Section II, J

  Statistical Modelling

  Part II, 2015

  An experiment is conducted where scientists count the numbers of each of three different strains of fleas that are reproducing in a controlled environment. Varying concentrations of a particular toxin that impairs reproduction are administered to the fleas. The results of the experiment are stored in a data frame $f l e a s$ in $\mathrm{R}$, whose first few rows are given below.

  

  The full dataset has 80 rows. The first column provides the number of fleas, the second provides the concentration of the toxin and the third specifies the strain of the flea as factors 0,1 or 2 . Strain 0 is the common flea and strains 1 and 2 have been genetically modified in a way thought to increase their ability to reproduce in the presence of the toxin.

  Explain and interpret the $\mathrm{R}$ commands and (abbreviated) output below. In particular, you should describe the model being fitted, briefly explain how the standard errors are calculated, and comment on the hypothesis tests being described in the summary.

  

  Explain and motivate the following $\mathrm{R}$ code in the light of the output above. Briefly explain the differences between the models fitted below, and the model corresponding to $f$ it $1 .$

  

  Denote by $M_{1}, M_{2}, M_{3}$ the three models being fitted in sequence above. Explain the hypothesis tests comparing the models to each other that can be performed using the output from the following $R$ code.

  $>c($ fit1$dev, fit2$dev, fit3$dev)

  [1] $56.8756 .9376 .98$

  $>\operatorname{qchisq}(0.95, \mathrm{df}=1)$

  [1] $3.84$

  Use these numbers to comment on the most appropriate model for the data.

  comment

• Paper 4, Section II, C

  Statistical Physics

  Part II, 2015

  The Ising model consists of $N$ particles, labelled by $i$, arranged on a $D$-dimensional Euclidean lattice with periodic boundary conditions. Each particle has spin up $s_{i}=+1$, or down $s_{i}=-1$, and the energy in the presence of a magnetic field $B$ is

  $$E=-B \sum_{i} s_{i}-J \sum_{\langle i, j\rangle} s_{i} s_{j}$$

  where $J>0$ is a constant and $\langle i, j\rangle$ indicates that the second sum is over each pair of nearest neighbours (every particle has $2 D$ nearest neighbours). Let $\beta=1 / k_{B} T$, where $T$ is the temperature.

  (i) Express the average spin per particle, $m=\left(\sum_{i}\left\langle s_{i}\right\rangle\right) / N$, in terms of the canonical partition function $Z$.

  (ii) Show that in the mean-field approximation

  $$Z=C\left[Z_{1}\left(\beta B_{\mathrm{eff}}\right)\right]^{N}$$

  where $Z_{1}$ is a single-particle partition function, $B_{\text {eff }}$ is an effective magnetic field which you should find in terms of $B, J, D$ and $m$, and $C$ is a prefactor which you should also evaluate.

  (iii) Deduce an equation that determines $m$ for general values of $B, J$ and temperature $T$. Without attempting to solve for $m$ explicitly, discuss how the behaviour of the system depends on temperature when $B=0$, deriving an expression for the critical temperature $T_{c}$ and explaining its significance.

  (iv) Comment briefly on whether the results obtained using the mean-field approximation for $B=0$ are consistent with an expression for the free energy of the form

  $$F(m, T)=F_{0}(T)+\frac{a}{2}\left(T-T_{c}\right) m^{2}+\frac{b}{4} m^{4}$$

  where $a$ and $b$ are positive constants.

  comment

• Paper 3, Section II, C

  Statistical Physics

  Part II, 2015

  (a) A sample of gas has pressure $p$, volume $V$, temperature $T$ and entropy $S$.

  (i) Use the first law of thermodynamics to derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial p}\right)_{T}=-\left(\frac{\partial V}{\partial T}\right)_{p} .$$

  (ii) Define the heat capacity at constant pressure $C_{p}$ and the enthalpy $H$ and show that $C_{p}=(\partial H / \partial T)_{p}$.

  (b) Consider a perfectly insulated pipe with a throttle valve, as shown.

  

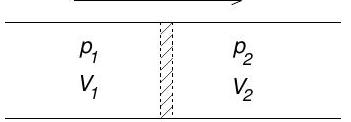
  Gas initially occupying volume $V_{1}$ on the left is forced slowly through the valve at constant pressure $p_{1}$. A constant pressure $p_{2}$ is maintained on the right and the final volume occupied by the gas after passing through the valve is $V_{2}$.

  (i) Show that the enthalpy $H$ of the gas is unchanged by this process.

  (ii) The Joule-Thomson coefficient is defined to be $\mu=(\partial T / \partial p)_{H}$. Show that

  $$\mu=\frac{V}{C_{p}}\left[\frac{T}{V}\left(\frac{\partial V}{\partial T}\right)_{p}-1\right]$$

  [You may assume the identity $(\partial y / \partial x)_{u}=-(\partial u / \partial x)_{y} /(\partial u / \partial y)_{x} \cdot$ ]

  (iii) Suppose that the gas obeys an equation of state

  $$p=k_{B} T\left[\frac{N}{V}+B_{2}(T) \frac{N^{2}}{V^{2}}\right]$$

  where $N$ is the number of particles. Calculate $\mu$ to first order in $N / V$ and hence derive a condition on $\frac{d}{d T}\left(\frac{B_{2}(T)}{T}\right)$ for obtaining a positive Joule-Thomson coefficient.

  comment

• Paper 2, Section II, C

  Statistical Physics

  Part II, 2015

  (a) State the Bose-Einstein distribution formula for the mean occupation numbers $n_{i}$ of discrete single-particle states $i$ with energies $E_{i}$ in a gas of bosons. Write down expressions for the total particle number $N$ and the total energy $U$ when the singleparticle states can be treated as continuous, with energies $E \geqslant 0$ and density of states $g(E)$.

  (b) Blackbody radiation at temperature $T$ is equivalent to a gas of photons with

  $$g(E)=A V E^{2}$$

  where $V$ is the volume and $A$ is a constant. What value of the chemical potential is required when applying the Bose-Einstein distribution to photons? Show that the heat capacity at constant volume satisfies $C_{V} \propto T^{\alpha}$ for some constant $\alpha$, to be determined.

  (c) Consider a system of bosonic particles of fixed total number $N \gg 1$. The particles are trapped in a potential which has ground state energy zero and which gives rise to a density of states $g(E)=B E^{2}$, where $B$ is a constant. Explain, for this system, what is meant by Bose-Einstein condensation and show that the critical temperature satisfies $T_{c} \propto N^{1 / 3}$. If $N_{0}$ is the number of particles in the ground state, show that for $T$ just below $T_{c}$

  $$N_{0} / N \approx 1-\left(T / T_{c}\right)^{\gamma}$$

  for some constant $\gamma$, to be determined.

  (d) Would you expect photons to exhibit Bose-Einstein condensation? Explain your answer very briefly.

  comment

• Paper 1, Section II, C

  Statistical Physics

  Part II, 2015

  (a) Define the canonical partition function $Z$ for a system with energy levels $E_{n}$, where $n$ labels states, given that the system is in contact with a heat reservoir at temperature $T$. What is the probability $p(n)$ that the system occupies state $n$ ? Starting from an expression for the entropy $S=k_{B} \partial(T \ln Z) / \partial T$, deduce that

  $$S=-k_{B} \sum_{n} p(n) \ln p(n)$$

  (b) Consider an ensemble consisting of $W$ copies of the system in part (a) with $W$ very large, so that there are $W p(n)$ members of the ensemble in state $n$. Starting from an expression for the number of ways in which this can occur, find the entropy $S_{W}$ of the ensemble and hence re-derive the expression $(*)$. [You may assume Stirling's formula $\ln X ! \approx X \ln X-X$ for $X$ large. $]$

  (c) Consider a system of $N$ non-interacting particles at temperature $T$. Each particle has $q$ internal states with energies

  $$0, \mathcal{E}, 2 \mathcal{E}, \ldots,(q-1) \mathcal{E}$$

  Assuming that the internal states are the only relevant degrees of freedom, calculate the total entropy of the system. Find the limiting values of the entropy as $T \rightarrow 0$ and $T \rightarrow \infty$ and comment briefly on your answers.

  comment

• Paper 4, Section II, $26 \mathrm{~K}$

  Stochastic Financial Models

  Part II, 2015

  (i) An investor in a single-period market with time- 0 wealth $w_{0}$ may generate any time-1 wealth $w_{1}$ of the form $w_{1}=w_{0}+X$, where $X$ is any element of a vector space $V$ of random variables. The investor's objective is to maximize $E\left[U\left(w_{1}\right)\right]$, where $U$ is strictly increasing, concave and $C^{2}$. Define the utility indifference price $\pi(Y)$ of a random variable $Y$.

  Prove that the map $Y \mapsto \pi(Y)$ is concave. [You may assume that any supremum is attained.]

  (ii) Agent $j$ has utility $U_{j}(x)=-\exp \left(-\gamma_{j} x\right), j=1, \ldots, J$. The agents may buy for time- 0 price $p$ a risky asset which will be worth $X$ at time 1 , where $X$ is random and has density

  $$f(x)=\frac{1}{2} \alpha e^{-\alpha|x|}, \quad-\infty<x<\infty .$$

  Assuming zero interest, prove that agent $j$ will optimally choose to buy

  $$\theta_{j}=-\frac{\sqrt{1+p^{2} \alpha^{2}}-1}{\gamma_{j} p}$$

  units of the risky asset at time 0 .

  If the asset is in unit net supply, if $\Gamma^{-1} \equiv \sum_{j} \gamma_{j}^{-1}$, and if $\alpha>\Gamma$, prove that the market for the risky asset will clear at price

  $$p=-\frac{2 \Gamma}{\alpha^{2}-\Gamma^{2}}$$

  What happens if $\alpha \leqslant \Gamma ?$

  comment

• Paper 3, Section II, $26 \mathrm{~K}$

  Stochastic Financial Models

  Part II, 2015

  A single-period market consists of $n$ assets whose prices at time $t$ are denoted by $S_{t}=\left(S_{t}^{1}, \ldots, S_{t}^{n}\right)^{T}, t=0,1$, and a riskless bank account bearing interest rate $r$. The value of $S_{0}$ is given, and $S_{1} \sim N(\mu, V)$. An investor with utility $U(x)=-\exp (-\gamma x)$ wishes to choose a portfolio of the available assets so as to maximize the expected utility of her wealth at time 1. Find her optimal investment.

  What is the market portfolio for this problem? What is the beta of asset $i$ ? Derive the Capital Asset Pricing Model, that

  Excess return of asset $i=$ Excess return of market portfolio $\times \beta_{i}$.

  The Sharpe ratio of a portfolio $\theta$ is defined to be the excess return of the portfolio $\theta$ divided by the standard deviation of the portfolio $\theta$. If $\rho_{i}$ is the correlation of the return on asset $i$ with the return on the market portfolio, prove that

  Sharpe ratio of asset $i=$ Sharpe ratio of market portfolio $\times \rho_{i}$.

  comment

• Paper 1, Section II, $26 K$

  Stochastic Financial Models

  Part II, 2015

  (i) What does it mean to say that $\left(X_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale?

  (ii) If $Y$ is an integrable random variable and $Y_{n}=E\left[Y \mid \mathcal{F}_{n}\right]$, prove that $\left(Y_{n}, \mathcal{F}_{n}\right)$ is a martingale. [Standard facts about conditional expectation may be used without proof provided they are clearly stated.] When is it the case that the limit $\lim _{n \rightarrow \infty} Y_{n}$ exists almost surely?

  (iii) An urn contains initially one red ball and one blue ball. A ball is drawn at random and then returned to the urn with a new ball of the other colour. This process is repeated, adding one ball at each stage to the urn. If the number of red balls after $n$ draws and replacements is $X_{n}$, and the number of blue balls is $Y_{n}$, show that $M_{n}=h\left(X_{n}, Y_{n}\right)$ is a martingale, where

  $$h(x, y)=(x-y)(x+y-1)$$

  Does this martingale converge almost surely?

  comment

• Paper 2, Section II, $27 \mathrm{~K}$

  Stochastic Financial Models

  Part II, 2015

  (i) What is Brownian motion?

  (ii) Suppose that $\left(B_{t}\right)_{t \geqslant 0}$ is Brownian motion, and the price $S_{t}$ at time $t$ of a risky asset is given by

  $$S_{t}=S_{0} \exp \left\{\sigma B_{t}+\left(\mu-\frac{1}{2} \sigma^{2}\right) t\right\}$$

  where $\mu>0$ is the constant growth rate, and $\sigma>0$ is the constant volatility of the asset. Assuming that the riskless rate of interest is $r>0$, derive an expression for the price at time 0 of a European call option with strike $K$ and expiry $T$, explaining briefly the basis for your calculation.

  (iii) With the same notation, derive the time-0 price of a European option with expiry $T$ which at expiry pays

  $$\left\{\left(S_{T}-K\right)^{+}\right\}^{2} / S_{T}$$

  comment

• Paper 2, Section II, $24 K$

  Applied Probability

  Part II, 2015

  (i) Defne a Poisson process on $\mathbb{R}_{+}$with rate $\lambda$. Let $N$ and $M$ be two independent Poisson processes on $\mathbb{R}_{+}$of rates $\lambda$ and $\mu$ respectively. Prove that $N+M$ is also a Poisson process and find its rate.

  (ii) Let $X$ be a discrete time Markov chain with transition matrix $K$ on the finite state space $S$. Find the generator of the continuous time Markov chain $Y_{t}=X_{N_{t}}$ in terms of $K$ and $\lambda$. Show that if $\pi$ is an invariant distribution for $X$, then it is also invariant for $Y$.

  Suppose that $X$ has an absorbing state $a$. If $\tau_{a}$ and $T_{a}$ are the absorption times for $X$ and $Y$ respectively, write an equation that relates $\mathbb{E}_{x}\left[\tau_{a}\right]$ and $\mathbb{E}_{x}\left[T_{a}\right]$, where $x \in S$.

  [Hint: You may want to prove that if $\xi_{1}, \xi_{2}, \ldots$ are i.i.d. non-negative random variables with $\mathbb{E}\left[\xi_{1}\right]<\infty$ and $M$ is an independent non-negative random variable, then $\left.\mathbb{E}\left[\sum_{i=1}^{M} \xi_{i}\right]=\mathbb{E}[M] \mathbb{E}\left[\xi_{1}\right] .\right]$

  comment

• Paper 4, Section I, $2 I$

  Topics in Analysis

  Part II, 2015

  Let $\mathcal{K}$ be the set of all non-empty compact subsets of $m$-dimensional Euclidean space $\mathbb{R}^{m}$. Define the Hausdorff metric on $\mathcal{K}$, and prove that it is a metric.

  Let $K_{1} \supseteq K_{2} \supseteq \ldots$ be a sequence in $\mathcal{K}$. Show that $K=\bigcap_{n=1}^{\infty} K_{n}$ is also in $\mathcal{K}$ and that $K_{n} \rightarrow K$ as $n \rightarrow \infty$ in the Hausdorff metric.

  comment

• Paper 3, Section I, $2 I$

  Topics in Analysis

  Part II, 2015

  Let $K$ be a compact subset of $\mathbb{C}$ with path-connected complement. If $w \notin K$ and $\epsilon>0$, show that there is a polynomial $P$ such that

  $$\left|P(z)-\frac{1}{w-z}\right| \leqslant \epsilon$$

  for all $z \in K$.

  comment

• Paper 2, Section I, I

  Topics in Analysis

  Part II, 2015

  Let $x_{1}, x_{2}, \ldots, x_{n}$ be the roots of the Legendre polynomial of degree $n$. Let $A_{1}$, $A_{2}, \ldots, A_{n}$ be chosen so that

  $$\int_{-1}^{1} p(t) d t=\sum_{j=1}^{n} A_{j} p\left(x_{j}\right)$$

  for all polynomials $p$ of degree $n-1$ or less. Assuming any results about Legendre polynomials that you need, prove the following results:

  (i) $\int_{-1}^{1} p(t) d t=\sum_{j=1}^{n} A_{j} p\left(x_{j}\right)$ for all polynomials $p$ of degree $2 n-1$ or less;

  (ii) $A_{j} \geqslant 0$ for all $1 \leqslant j \leqslant n$;

  (iii) $\sum_{j=1}^{n} A_{j}=2$.

  Now consider $Q_{n}(f)=\sum_{j=1}^{n} A_{j} f\left(x_{j}\right)$. Show that

  $$Q_{n}(f) \rightarrow \int_{-1}^{1} f(t) d t$$

  as $n \rightarrow \infty$ for all continuous functions $f$.

  comment

• Paper 1, Section I, I

  Topics in Analysis

  Part II, 2015

  Let $\Omega$ be a non-empty bounded open subset of $\mathbb{R}^{2}$ with closure $\bar{\Omega}$ and boundary $\partial \Omega$. Let $\phi: \bar{\Omega} \rightarrow \mathbb{R}$ be continuous with $\phi$ twice differentiable on $\Omega$.

  (i) Why does $\phi$ have a maximum on $\bar{\Omega}$ ?

  (ii) If $\epsilon>0$ and $\nabla^{2} \phi \geqslant \epsilon$ on $\Omega$, show that $\phi$ has a maximum on $\partial \Omega$.

  (iii) If $\nabla^{2} \phi \geqslant 0$ on $\Omega$, show that $\phi$ has a maximum on $\partial \Omega$.

  (iv) If $\nabla^{2} \phi=0$ on $\Omega$ and $\phi=0$ on $\partial \Omega$, show that $\phi=0$ on $\bar{\Omega}$.

  comment

• Paper 2, Section II,

  Topics in Analysis

  Part II, 2015

  State and prove Sperner's lemma concerning the colouring of triangles.

  Deduce a theorem, to be stated clearly, on retractions to the boundary of a disc.

  State Brouwer's fixed point theorem for a disc and sketch a proof of it.

  Let $g: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ be a continuous function such that for some $K>0$ we have $\|g(x)-x\| \leqslant K$ for all $x \in \mathbb{R}^{2}$. Show that $g$ is surjective.

  comment

• Paper 3, Section II, I

  Topics in Analysis

  Part II, 2015

  Let $\alpha>0$. By considering the set $E_{m}$ consisting of those $f \in C([0,1])$ for which there exists an $x \in[0,1]$ with $|f(x+h)-f(x)| \leqslant m|h|^{\alpha}$ for all $x+h \in[0,1]$, or otherwise, give a Baire category proof of the existence of continuous functions $f$ on $[0,1]$ such that

  $$\limsup _{h \rightarrow 0}|h|^{-\alpha}|f(x+h)-f(x)|=\infty$$

  at each $x \in[0,1]$.

  Are the following statements true? Give reasons.

  (i) There exists an $f \in C([0,1])$ such that

  $$\limsup _{h \rightarrow 0}|h|^{-\alpha}|f(x+h)-f(x)|=\infty$$

  for each $x \in[0,1]$ and each $\alpha>0$.

  (ii) There exists an $f \in C([0,1])$ such that

  $$\limsup _{h \rightarrow 0}|h|^{-\alpha}|f(x+h)-f(x)|=\infty$$

  for each $x \in[0,1]$ and each $\alpha \geqslant 0$.

  comment

• Paper 4, Section II, 36B

  Waves

  Part II, 2015

  The shallow-water equations

  $$\frac{\partial h}{\partial t}+u \frac{\partial h}{\partial x}+h \frac{\partial u}{\partial x}=0, \quad \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+g \frac{\partial h}{\partial x}=0$$

  describe one-dimensional flow over a horizontal boundary with depth $h(x, t)$ and velocity $u(x, t)$, where $g$ is the acceleration due to gravity.

  Show that the Riemann invariants $u \pm 2\left(c-c_{0}\right)$ are constant along characteristics $C_{\pm}$satisfying $d x / d t=u \pm c$, where $c(h)$ is the linear wave speed and $c_{0}$ denotes a reference state.

  An initially stationary pool of fluid of depth $h_{0}$ is held between a stationary wall at $x=a>0$ and a removable barrier at $x=0$. At $t=0$ the barrier is instantaneously removed allowing the fluid to flow into the region $x<0$.

  For $0 \leqslant t \leqslant a / c_{0}$, find $u(x, t)$ and $c(x, t)$ in each of the regions

  $$\begin{gathered} \text { (i) } \quad c_{0} t \leqslant x \leqslant a \\ \text { (ii) }-2 c_{0} t \leqslant x \leqslant c_{0} t \end{gathered}$$

  explaining your argument carefully with a sketch of the characteristics in the $(x, t)$ plane.

  For $t \geqslant a / c_{0}$, show that the solution in region (ii) above continues to hold in the region $-2 c_{0} t \leqslant x \leqslant 3 a\left(c_{0} t / a\right)^{1 / 3}-2 c_{0} t$. Explain why this solution does not hold in $3 a\left(c_{0} t / a\right)^{1 / 3}-2 c_{0} t<x<a .$

  comment

• Paper 2, Section II, 36B

  Waves

  Part II, 2015

  A uniform elastic solid with density $\rho$ and Lamé moduli $\lambda$ and $\mu$ occupies the region between rigid plane boundaries $z=0$ and $z=h$. Starting with the linear elastic wave equation, show that SH waves can propagate in the $x$-direction within this waveguide, and find the dispersion relation $\omega(k)$ for the various modes.

  State the cut-off frequency for each mode. Find the corresponding phase velocity $c(k)$ and group velocity $c_{g}(k)$, and sketch these functions for $k, \omega>0$.

  Define the time and cross-sectional average appropriate for a mode with frequency $\mathrm{~}$energy. [You may assume that the elastic energy per unit volume is $\frac{1}{2}\left(\lambda e_{k k}^{2}+2 \mu e_{i j} e_{i j}\right)$.]

  An elastic displacement of the form $\mathbf{u}=(0, f(x, z), 0)$ is created in a region near $x=0$, and then released at $t=0$. Explain briefly how the amplitude of the resulting disturbance varies with time as $t \rightarrow \infty$ at the moving position $x=V t$ for each of the cases $0<V^{2}<\mu / \rho$ and $V^{2}>\mu / \rho$. [You may quote without proof any generic results from the method of stationary phase.]

  comment

• Paper 3, Section II, B

  Waves

  Part II, 2015

  Derive the ray-tracing equations for the quantities $\mathrm{d} k_{i} / \mathrm{d} t, \mathrm{~d} \omega / \mathrm{d} t$ and $\mathrm{d} x_{i} / \mathrm{d} t$ during wave propagation through a slowly varying medium with local dispersion relation $\omega=\Omega(\mathbf{k}, \mathbf{x}, t)$, explaining the meaning of the notation $\mathrm{d} / \mathrm{d} t$.

  The dispersion relation for water waves is $\Omega^{2}=g \kappa \tanh (\kappa h)$, where $h$ is the water depth, $\kappa^{2}=k^{2}+l^{2}$, and $k$ and $l$ are the components of $\mathbf{k}$ in the horizontal $x$ and $y$ directions. Water waves are incident from an ocean occupying $x>0,-\infty<y<\infty$ onto a beach at $x=0$. The undisturbed water depth is $h(x)=\alpha x^{p}$, where $\alpha, p$ are positive constants and $\alpha$ is sufficiently small that the depth can be assumed to be slowly varying. Far from the beach, the waves are planar with frequency $\omega_{\infty}$ and with crests making an acute angle $\theta_{\infty}$ with the shoreline.

  Obtain a differential equation (with $k$ defined implicitly) for a ray $y=y(x)$ and show that near the shore the ray satisfies

  $$y-y_{0} \sim A x^{q}$$

  where $A$ and $q$ should be found. Sketch the shape of the wavecrests near the shoreline for the case $p<2$.

  comment

• Paper 1, Section II, 37B

  Waves

  Part II, 2015

  An acoustic plane wave (not necessarily harmonic) travels at speed $c_{0}$ in the direction $\hat{\mathbf{k}}$, where $|\hat{\mathbf{k}}|=1$, through an inviscid, compressible fluid of unperturbed density $\rho_{0}$. Show that the velocity $\tilde{\mathbf{u}}$ is proportional to the perturbation pressure $\tilde{p}$, and find $\tilde{\mathbf{u}} / \tilde{p}$. Define the acoustic intensity $\mathbf{I}$.

  A harmonic acoustic plane wave with wavevector $\mathbf{k}=k(\cos \theta, \sin \theta, 0)$ and unitamplitude perturbation pressure is incident from $x<0$ on a thin elastic membrane at unperturbed position $x=0$. The regions $x<0$ and $x>0$ are both occupied by gas with density $\rho_{0}$ and sound speed $c_{0}$. The kinematic boundary conditions at the membrane are those appropriate for an inviscid fluid, and the (linearized) dynamic boundary condition

  $$m \frac{\partial^{2} X}{\partial t^{2}}-T \frac{\partial^{2} X}{\partial y^{2}}+[\tilde{p}(0, y, t)]_{-}^{+}=0$$

  where $T$ and $m$ are the tension and mass per unit area of the membrane, and $x=X(y, t)$ (with $|k X| \ll 1$ ) is its perturbed position. Find the amplitudes of the reflected and transmitted pressure perturbations, expressing your answers in terms of the dimensionless parameter

  $$\alpha=\frac{\rho_{0} c_{0}^{2}}{k \cos \theta\left(m c_{0}^{2}-T \sin ^{2} \theta\right)} .$$

  Hence show that the time-averaged energy flux in the $x$-direction is conserved across the membrane.

  comment

• Paper 1, Section II, K

  Applied Probability

  Part II, 2015

  (a) Give the definition of a birth and death chain in terms of its generator. Show that a measure $\pi$ is invariant for a birth and death chain if and only if it solves the detailed balance equations.

  (b) There are $s$ servers in a post office and a single queue. Customers arrive as a Poisson process of rate $\lambda$ and the service times at each server are independent and exponentially distributed with parameter $\mu$. Let $X_{t}$ denote the number of customers in the post office at time $t$. Find conditions on $\lambda, \mu$ and $s$ for $X$ to be positive recurrent, null recurrent and transient, justifying your answers.

  comment

• Paper 4, Section II, C

  Asymptotic Methods

  Part II, 2015

  Consider the ordinary differential equation

  $$\frac{d^{2} u}{d z^{2}}+f(z) \frac{d u}{d z}+g(z) u=0$$

  where

  $$f(z) \sim \sum_{m=0}^{\infty} \frac{f_{m}}{z^{m}}, \quad g(z) \sim \sum_{m=0}^{\infty} \frac{g_{m}}{z^{m}}, \quad z \rightarrow \infty$$

  and $f_{m}, g_{m}$ are constants. Look for solutions in the asymptotic form

  $$u(z)=e^{\lambda z} z^{\mu}\left[1+\frac{a}{z}+\frac{b}{z^{2}}+O\left(\frac{1}{z^{3}}\right)\right], \quad z \rightarrow \infty$$

  and determine $\lambda$ in terms of $\left(f_{0}, g_{0}\right)$, as well as $\mu$ in terms of $\left(\lambda, f_{0}, f_{1}, g_{1}\right)$.

  Deduce that the Bessel equation

  $$\frac{d^{2} u}{d z^{2}}+\frac{1}{z} \frac{d u}{d z}+\left(1-\frac{\nu^{2}}{z^{2}}\right) u=0$$

  where $\nu$ is a complex constant, has two solutions of the form

  $$\begin{aligned} &u^{(1)}(z)=\frac{e^{i z}}{z^{1 / 2}}\left[1+\frac{a^{(1)}}{z}+O\left(\frac{1}{z^{2}}\right)\right], \quad z \rightarrow \infty \\ &u^{(2)}(z)=\frac{e^{-i z}}{z^{1 / 2}}\left[1+\frac{a^{(2)}}{z}+O\left(\frac{1}{z^{2}}\right)\right], \quad z \rightarrow \infty \end{aligned}$$

  and determine $a^{(1)}$ and $a^{(2)}$ in terms of $\nu .$

  Can the above asymptotic expansions be valid for all $\arg (z)$, or are they valid only in certain domains of the complex $z$-plane? Justify your answer briefly.

  comment

• Paper 3, Section II, $27 \mathrm{C}$

  Asymptotic Methods

  Part II, 2015

  Show that

  $$\int_{0}^{1} e^{i k t^{3}} d t=I_{1}-I_{2}, \quad k>0$$

  where $I_{1}$ is an integral from 0 to $\infty$ along the line $\arg (z)=\frac{\pi}{6}$ and $I_{2}$ is an integral from 1 to $\infty$ along a steepest-descent contour $C$ which you should determine.

  By employing in the integrals $I_{1}$ and $I_{2}$ the changes of variables $u=-i z^{3}$ and $u=-i\left(z^{3}-1\right)$, respectively, compute the first two terms of the large $k$ asymptotic expansion of the integral above.

  comment

• Paper 1, Section II, C

  Asymptotic Methods

  Part II, 2015

  (a) State the integral expression for the gamma function $\Gamma(z)$, for $\operatorname{Re}(z)>0$, and express the integral

  $$\int_{0}^{\infty} t^{\gamma-1} e^{i t} d t, \quad 0<\gamma<1$$

  in terms of $\Gamma(\gamma)$. Explain why the constraints on $\gamma$ are necessary.

  (b) Show that

  $$\int_{0}^{\infty} \frac{e^{-k t^{2}}}{\left(t^{2}+t\right)^{\frac{1}{4}}} d t \sim \sum_{m=0}^{\infty} \frac{a_{m}}{k^{\alpha+\beta m}}, \quad k \rightarrow \infty$$

  for some constants $a_{m}, \alpha$ and $\beta$. Determine the constants $\alpha$ and $\beta$, and express $a_{m}$ in terms of the gamma function.

  State without proof the basic result needed for the rigorous justification of the above asymptotic formula.

  [You may use the identity:

  $$\left.(1+z)^{\alpha}=\sum_{m=0}^{\infty} c_{m} z^{m}, \quad c_{m}=\frac{\Gamma(\alpha+1)}{m ! \Gamma(\alpha+1-m)}, \quad|z|<1 .\right]$$

  comment

• Paper 4, Section I, D

  Classical Dynamics

  Part II, 2015

  A triatomic molecule is modelled by three masses moving in a line while connected to each other by two identical springs of force constant $k$ as shown in the figure.

  

  (a) Write down the Lagrangian and derive the equations describing the motion of the atoms.

  (b) Find the normal modes and their frequencies. What motion does the lowest frequency represent?

  comment

• Paper 2, Section II, F

  Algebraic Geometry

  Part II, 2015

  (i) Define the radical of an ideal.

  (ii) Assume the following statement: If $k$ is an algebraically closed field and $I \subseteq$ $k\left[x_{1}, \ldots, x_{n}\right]$ is an ideal, then either $I=(1)$ or $Z(I) \neq \emptyset$. Prove the Hilbert Nullstellensatz, namely that if $I \subseteq k\left[x_{1}, \ldots, x_{n}\right]$ with $k$ algebraically closed, then

  $$I(Z(I))=\sqrt{I}$$

  (iii) Show that if $A$ is a commutative ring and $I, J \subseteq A$ are ideals, then

  $$\sqrt{I \cap J}=\sqrt{I} \cap \sqrt{J} .$$

  (iv) Is

  $$\sqrt{I+J}=\sqrt{I}+\sqrt{J} ?$$

  Give a proof or a counterexample.

  comment

• Paper 3, Section I, $7 \mathrm{D}$

  Classical Dynamics

  Part II, 2015

  (a) Consider a particle of mass $m$ that undergoes periodic motion in a one-dimensional potential $V(q)$. Write down the Hamiltonian $H(p, q)$ for the system. Explain what is meant by the angle-action variables $(\theta, I)$ of the system and write down the integral expression for the action variable $I$.

  (b) For $V(q)=\frac{1}{2} m \omega^{2} q^{2}$ and fixed total energy $E$, describe the shape of the trajectories in phase-space. By using the expression for the area enclosed by the trajectory, or otherwise, find the action variable $I$ in terms of $\omega$ and $E$. Hence describe how $E$ changes with $\omega$ if $\omega$ varies slowly with time. Justify your answer.

  comment

• Paper 2, Section I, D

  Classical Dynamics

  Part II, 2015

  The Lagrangian for a heavy symmetric top of mass $M$, pinned at a point that is a distance $l$ from the centre of mass, is

  $$L=\frac{1}{2} I_{1}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-M g l \cos \theta$$

  (a) Find all conserved quantities. In particular, show that $\omega_{3}$, the spin of the top, is constant.

  (b) Show that $\theta$ obeys the equation of motion

  $$I_{1} \ddot{\theta}=-\frac{d V_{\text {eff }}}{d \theta},$$

  where the explicit form of $V_{\text {eff }}$ should be determined.

  (c) Determine the condition for uniform precession with no nutation, that is $\dot{\theta}=0$ and $\dot{\phi}=$ const. For what values of $\omega_{3}$ does such uniform precession occur?

  comment

• Paper 1, Section I, D

  Classical Dynamics

  Part II, 2015

  (a) The action for a one-dimensional dynamical system with a generalized coordinate $q$ and Lagrangian $L$ is given by

  $$S=\int_{t_{1}}^{t_{2}} L(q, \dot{q}, t) d t$$

  State the principle of least action and derive the Euler-Lagrange equation.

  (b) A planar spring-pendulum consists of a light rod of length $l$ and a bead of mass $m$, which is able to slide along the rod without friction and is attached to the ends of the rod by two identical springs of force constant $k$ as shown in the figure. The rod is pivoted at one end and is free to swing in a vertical plane under the influence of gravity.

  

  (i) Identify suitable generalized coordinates and write down the Lagrangian of the system.

  (ii) Derive the equations of motion.

  comment

• Paper 4, Section II, C

  Classical Dynamics

  Part II, 2015

  Consider a rigid body with angular velocity $\boldsymbol{\omega}$, angular momentum $\mathbf{L}$ and position vector $\mathbf{r}$, in its body frame.

  (a) Use the expression for the kinetic energy of the body,

  $$\frac{1}{2} \int d^{3} \mathbf{r} \rho(\mathbf{r}) \dot{\mathbf{r}}^{2},$$

  to derive an expression for the tensor of inertia of the body, I. Write down the relationship between $\mathbf{L}, \mathbf{I}$ and $\boldsymbol{\omega}$.

  (b) Euler's equations of torque-free motion of a rigid body are

  $$\begin{aligned} &I_{1} \dot{\omega}_{1}=\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3} \\ &I_{2} \dot{\omega}_{2}=\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1} \\ &I_{3} \dot{\omega}_{3}=\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2} \end{aligned}$$

  Working in the frame of the principal axes of inertia, use Euler's equations to show that the energy $E$ and the squared angular momentum $\mathbf{L}^{2}$ are conserved.

  (c) Consider a cuboid with sides $a, b$ and $c$, and with mass $M$ distributed uniformly.

  (i) Use the expression for the tensor of inertia derived in (a) to calculate the principal moments of inertia of the body.

  (ii) Assume $b=2 a$ and $c=4 a$, and suppose that the initial conditions are such that

  $$\mathbf{L}^{2}=2 I_{2} E$$

  with the initial angular velocity $\omega$ perpendicular to the intermediate principal axis $\mathbf{e}_{2}$. Derive the first order differential equation for $\omega_{2}$ in terms of $E, M$ and $a$ and hence determine the long-term behaviour of $\boldsymbol{\omega}$.

  comment

• Paper 2, Section II, C

  Classical Dynamics

  Part II, 2015

  (a) Consider a Lagrangian dynamical system with one degree of freedom. Write down the expression for the Hamiltonian of the system in terms of the generalized velocity $\dot{q}$, momentum $p$, and the Lagrangian $L(q, \dot{q}, t)$. By considering the differential of the Hamiltonian, or otherwise, derive Hamilton's equations.

  Show that if $q$ is ignorable (cyclic) with respect to the Lagrangian, i.e. $\partial L / \partial q=0$, then it is also ignorable with respect to the Hamiltonian.

  (b) A particle of charge $q$ and mass $m$ moves in the presence of electric and magnetic fields such that the scalar and vector potentials are $\phi=y E$ and $\mathbf{A}=(0, x B, 0)$, where $(x, y, z)$ are Cartesian coordinates and $E, B$ are constants. The Lagrangian of the particle is

  $$L=\frac{1}{2} m \dot{\mathbf{r}}^{2}-q \phi+q \dot{\mathbf{r}} \cdot \mathbf{A}$$

  Starting with the Lagrangian, derive an explicit expression for the Hamiltonian and use Hamilton's equations to determine the motion of the particle.

  comment

• Paper 4, Section I, G

  Coding and Cryptography

  Part II, 2015

  Explain how to construct binary Reed-Muller codes. State and prove a result giving the minimum distance for each such Reed-Muller code.

  comment

• Paper 3, Section I, G

  Coding and Cryptography

  Part II, 2015

  Let $A$ be a random variable that takes each value $a$ in the finite alphabet $\mathcal{A}$ with probability $p(a)$. Show that, if each $l(a)$ is an integer greater than 0 and $\sum 2^{-l(a)} \leqslant 1$, then there is a decodable binary code $c: \mathcal{A} \rightarrow\{0,1\}^{*}$ with each codeword $c(a)$ having length $l(a)$.

  Prove that, for any decodable code $c: \mathcal{A} \rightarrow\{0,1\}^{*}$, we have

  $$H(A) \leqslant \mathbb{E} l(A)$$

  where $H(A)$ is the entropy of the random variable $A$. When is there equality in this inequality?

  comment

• Paper 2, Section I, G

  Coding and Cryptography

  Part II, 2015

  A random variable $A$ takes values in the alphabet $\mathcal{A}=\{a, b, c, d, e\}$ with probabilities $0.4,0.2,0.2,0.1$ and $0.1$. Calculate the entropy of $A$.

  Define what it means for a code for a general finite alphabet to be optimal. Find such a code for the distribution above and show that there are optimal codes for this distribution with differing lengths of codeword.

  [You may use any results from the course without proof. Note that $\log _{2} 5 \simeq 2.32$.]

  comment

• Paper 1, Section I, $3 G$

  Coding and Cryptography

  Part II, 2015

  Let $\mathcal{A}$ be a finite alphabet. Explain what is meant by saying that a binary code $c: \mathcal{A} \rightarrow\{0,1\}^{*}$ has minimum distance $\delta$. If $c$ is such a binary code with minimum distance $\delta$, show that $c$ is $\delta-1$ error-detecting and $\left\lfloor\frac{1}{2}(\delta-1)\right\rfloor$ error-correcting.

  Show that it is possible to construct a code that has minimum distance $\delta$ for any integer $\delta>0$.

  comment

• Paper 1, Section II, G

  Coding and Cryptography

  Part II, 2015

  Define the Hamming code. Show that it is a perfect, linear, 1-error correcting code.

  I wish to send a message through a noisy channel to a friend. The message consists of a large number $N=1,000$ of letters from a 16 -letter alphabet $\mathcal{A}$. When my friend has decoded the message, she can tell whether there have been any errors. If there have, she asks me to send the message again and this is repeated until she has received the message without error. For each individual binary digit that is transmitted, there is independently a small probability $p=0.001$ of an error.

  (a) Suppose that I encode my message by writing each letter as a 4-bit binary string. The whole message is then $4 N$ bits long. What is the probability $P$ that the entire message is transmitted without error? How many times should I expect to transmit the message until my friend receives it without error?

  (b) As an alternative, I use the Hamming code to encode each letter of $\mathcal{A}$ as a 7-bit binary string. What is the probability that my friend can decode a single 7-bit string correctly? Deduce that the probability $Q$ that the entire message is correctly decoded is given approximately by

  $$Q \simeq\left(1-21 p^{2}\right)^{N} \simeq \exp \left(-21 N p^{2}\right)$$

  Which coding method is better?

  comment

• Paper 1, Section II, F

  Algebraic Geometry

  Part II, 2015

  Let $k$ be an algebraically closed field.

  (i) Let $X$ and $Y$ be affine varieties defined over $k$. Given a map $f: X \rightarrow Y$, define what it means for $f$ to be a morphism of affine varieties.

  (ii) With $X, Y$ still affine varieties over $k$, show that there is a one-to-one correspondence between $\operatorname{Hom}(X, Y)$, the set of morphisms between $X$ and $Y$, and $\operatorname{Hom}(A(Y), A(X))$, the set of $k$-algebra homomorphisms between $A(Y)$ and $A(X)$.

  (iii) Let $f: \mathbb{A}^{2} \rightarrow \mathbb{A}^{4}$ be given by $f(t, u)=\left(u, t, t^{2}, t u\right)$. Show that the image of $f$ is an affine variety $X$, and find a set of generators for $I(X)$.

  comment

• Paper 2, Section II, G

  Coding and Cryptography

  Part II, 2015

  Briefly describe the $R S A$ public key cipher.

  Just before it went into liquidation, the Internet Bank decided that it wanted to communicate with each of its customers using an RSA cipher. So, it chose a large modulus $N$, which is the product of two large prime numbers, and chose encrypting exponents $e_{j}$ and decrypting exponents $d_{j}$ for each customer $j$. The bank published $N$ and $e_{j}$ and sent the decrypting exponent $d_{j}$ secretly to customer $j$. Show explicitly that the cipher can be broken by each customer.

  The bank sent out the same message to each customer. I am not a customer of the bank but have two friends who are and I notice that their published encrypting exponents are coprime. Explain how I can find the original message. Can I break the cipher?

  comment

• Paper 4, Section I, C

  Cosmology

  Part II, 2015

  Calculate the total effective number of relativistic spin states $g_{*}$ present in the early universe when the temperature $T$ is $10^{10} \mathrm{~K}$ if there are three species of low-mass neutrinos and antineutrinos in addition to photons, electrons and positrons. If the weak interaction rate is $\Gamma=\left(T / 10^{10} \mathrm{~K}\right)^{5} \mathrm{~s}^{-1}$ and the expansion rate of the universe is $H=\sqrt{8 \pi G \rho / 3}$, where $\rho$ is the total density of the universe, calculate the temperature $T_{*}$ at which the neutrons and protons cease to interact via weak interactions, and show that $T_{*} \propto g_{*}^{1 / 6}$.

  State the formula for the equilibrium ratio of neutrons to protons at $T_{*}$, and briefly describe the sequence of events as the temperature falls from $T_{*}$ to the temperature at which the nucleosynthesis of helium and deuterium ends.

  What is the effect of an increase or decrease of $g_{*}$ on the abundance of helium-4 resulting from nucleosynthesis? Why do changes in $g_{*}$ have a very small effect on the final abundance of deuterium?

  comment

• Paper 3, Section I, C

  Cosmology

  Part II, 2015

  What is the flatness problem? Show by reference to the Friedmann equation how a period of accelerated expansion of the scale factor $a(t)$ in the early stages of the universe can solve the flatness problem if $\rho+3 P<0$, where $\rho$ is the mass density and $P$ is the pressure.

  In the very early universe, where we can neglect the spatial curvature and the cosmological constant, there is a homogeneous scalar field $\phi$ with a vacuum potential energy

  $$V(\phi)=m^{2} \phi^{2},$$

  and the Friedmann energy equation (in units where $8 \pi G=1$ ) is

  $$3 H^{2}=\frac{1}{2} \dot{\phi}^{2}+V(\phi),$$

  where $H$ is the Hubble parameter. The field $\phi$ obeys the evolution equation

  $$\ddot{\phi}+3 H \dot{\phi}+\frac{d V}{d \phi}=0$$

  During inflation, $\phi$ evolves slowly after starting from a large initial value $\phi_{i}$ at $t=0$. State what is meant by the slow-roll approximation. Show that in this approximation,

  $$\begin{aligned} \phi(t) &=\phi_{i}-\frac{2}{\sqrt{3}} m t \\ a(t) &=a_{i} \exp \left[\frac{m \phi_{i}}{\sqrt{3}} t-\frac{1}{3} m^{2} t^{2}\right]=a_{i} \exp \left[\frac{\phi_{i}^{2}-\phi^{2}(t)}{4}\right] \end{aligned}$$

  where $a_{i}$ is the initial value of $a$.

  As $\phi(t)$ decreases from its initial value $\phi_{i}$, what is its approximate value when the slow-roll approximation fails?

  comment

• Paper 2, Section I, C

  Cosmology

  Part II, 2015

  The mass density perturbation equation for non-relativistic matter $\left(P \ll \rho c^{2}\right)$ with wave number $k$ in the late universe $\left(t>t_{\mathrm{eq}}\right)$ is

  $$\ddot{\delta}+2 \frac{\dot{a}}{a} \dot{\delta}-\left(4 \pi G \rho-\frac{c_{s}^{2} k^{2}}{a^{2}}\right) \delta=0 .$$

  Suppose that a non-relativistic fluid with the equation of state $P \propto \rho^{4 / 3}$ dominates the universe when $a(t)=t^{2 / 3}$, and the curvature and the cosmological constant can be neglected. Show that the sound speed can be written in the form $c_{s}^{2}(t) \equiv d P / d \rho=$ $\bar{c}_{s}^{2} t^{-2 / 3}$ where $\bar{c}_{s}$ is a constant.

  Find power-law solutions to $(*)$ of the form $\delta \propto t^{\beta}$ and hence show that the general solution is

  $$\delta=A_{k} t^{n_{+}}+B_{k} t^{n_{-}}$$

  where

  $$n_{\pm}=-\frac{1}{6} \pm\left[\left(\frac{5}{6}\right)^{2}-\bar{c}_{s}^{2} k^{2}\right]^{1 / 2}$$

  Interpret your solutions in the two regimes $k \ll k_{J}$ and $k \gg k_{J}$ where $k_{J}=\frac{5}{6 \bar{c}_{s}}$.

  comment

• Paper 1, Section I, C

  Cosmology

  Part II, 2015

  Consider three galaxies $O, A$ and $B$ with position vectors $\mathbf{r}_{O}, \mathbf{r}_{A}$ and $\mathbf{r}_{B}$ in a homogeneous universe. Assuming they move with non-relativistic velocities $\mathbf{v}_{O}=\mathbf{0}, \mathbf{v}_{A}$ and $\mathbf{v}_{B}$, show that spatial homogeneity implies that the velocity field $\mathbf{v}(\mathbf{r})$ satisfies

  $$\mathbf{v}\left(\mathbf{r}_{B}-\mathbf{r}_{A}\right)=\mathbf{v}\left(\mathbf{r}_{B}-\mathbf{r}_{O}\right)-\mathbf{v}\left(\mathbf{r}_{A}-\mathbf{r}_{O}\right)$$

  and hence that $\mathbf{v}$ is linearly related to $\mathbf{r}$ by

  $$v_{i}=\sum_{j=1}^{3} H_{i j} r_{j}$$

  where the components of the matrix $H_{i j}$ are independent of $\mathbf{r}$.

  Suppose the matrix $H_{i j}$ has the form

  $$H_{i j}=\frac{D}{t}\left(\begin{array}{ccc} 5 & -1 & -2 \\ 1 & 5 & -1 \\ 2 & 1 & 5 \end{array}\right)$$

  with $D>0$ constant. Describe the kinematics of the cosmological expansion.

  comment

• Paper 3, Section II, C

  Cosmology

  Part II, 2015

  Massive particles and antiparticles each with mass $m$ and respective number densities $n(t)$ and $\bar{n}(t)$ are present at time $t$ in the radiation era of an expanding universe with zero curvature and no cosmological constant. Assuming they interact with crosssection $\sigma$ at speed $v$, explain, by identifying the physical significance of each of the terms, why the evolution of $n(t)$ is described by

  $$\frac{d n}{d t}=-3 \frac{\dot{a}}{a} n-\langle\sigma v\rangle n \bar{n}+P(t)$$

  where the expansion scale factor of the universe is $a(t)$, and where the meaning of $P(t)$ should be briefly explained. Show that

  $$(n-\bar{n}) a^{3}=\text { constant }$$

  Assuming initial particle-antiparticle symmetry, show that

  $$\frac{d\left(n a^{3}\right)}{d t}=\langle\sigma v\rangle\left(n_{\mathrm{eq}}^{2}-n^{2}\right) a^{3}$$

  where $n_{\mathrm{eq}}$ is the equilibrium number density at temperature $T$.

  Let $Y=n / T^{3}$ and $x=m / T$. Show that

  $$\frac{d Y}{d x}=-\frac{\lambda}{x^{2}}\left(Y^{2}-Y_{\mathrm{eq}}^{2}\right)$$

  where $\lambda=m^{3}\langle\sigma v\rangle / H_{m}$ and $H_{m}$ is the Hubble expansion rate when $T=m$.

  When $x>x_{f} \simeq 10$, the number density $n$ can be assumed to be depleted only by annihilations. If $\lambda$ is constant, show that as $x \rightarrow \infty$ at late time, $Y$ approaches a constant value given by

  $$Y=\frac{x_{f}}{\lambda}$$

  Why do you expect weakly interacting particles to survive in greater numbers than strongly interacting particles?

  comment

• Paper 1, Section II, C

  Cosmology

  Part II, 2015

  A closed universe contains black-body radiation, has a positive cosmological constant $\Lambda$, and is governed by the equation

  $$\frac{\dot{a}^{2}}{a^{2}}=\frac{\Gamma}{a^{4}}-\frac{1}{a^{2}}+\frac{\Lambda}{3},$$

  where $a(t)$ is the scale factor and $\Gamma$ is a positive constant. Using the substitution $y=a^{2}$ and the boundary condition $y(0)=0$, deduce the boundary condition for $\dot{y}(0)$ and show that

  $$\ddot{y}=\frac{4 \Lambda}{3} y-2$$

  and hence that

  $$a^{2}(t)=\frac{3}{2 \Lambda}\left[1-\cosh \left(\sqrt{\frac{4 \Lambda}{3}} t\right)+\lambda \sinh \left(\sqrt{\frac{4 \Lambda}{3}} t\right)\right]$$

  Express the constant $\lambda$ in terms of $\Lambda$ and $\Gamma$.

  Sketch the graphs of $a(t)$ for the cases $\lambda>1$ and $0<\lambda<1$.

  comment

• Paper 4, Section II, G

  Differential Geometry

  Part II, 2015

  Let $\mathrm{U}(n)$ denote the set of $n \times n$ unitary complex matrices. Show that $\mathrm{U}(n)$ is a smooth (real) manifold, and find its dimension. [You may use any general results from the course provided they are stated correctly.] For $A$ any matrix in $\mathrm{U}(n)$ and $H$ an $n \times n$ complex matrix, determine when $H$ represents a tangent vector to $\mathrm{U}(n)$ at $A$.

  Consider the tangent spaces to $\mathrm{U}(n)$ equipped with the metric induced from the standard (Euclidean) inner product $\langle\cdot, \cdot\rangle$ on the real vector space of $n \times n$ complex matrices, given by $\langle L, K\rangle=\operatorname{Re} \operatorname{trace}\left(L K^{*}\right)$, where $\operatorname{Re}$ denotes the real part and $K^{*}$ denotes the conjugate transpose of $K$. Suppose that $H$ represents a tangent vector to $\mathrm{U}(n)$ at the identity matrix $I$. Sketch an explicit construction of a geodesic curve on $\mathrm{U}(n)$ passing through $I$ and with tangent direction $H$, giving a brief proof that the acceleration of the curve is always orthogonal to the tangent space to $\mathrm{U}(n)$.

  [Hint: You will find it easier to work directly with $n \times n$ complex matrices, rather than the corresponding $2 n \times 2 n$ real matrices.]

  comment

• Paper 3 , Section II, G

  Differential Geometry

  Part II, 2015

  Show that the surface $S$ of revolution $x^{2}+y^{2}=\cosh ^{2} z$ in $\mathbb{R}^{3}$ is homeomorphic to a cylinder and has everywhere negative Gaussian curvature. Show moreover the existence of a closed geodesic on $S$.

  Let $S \subset \mathbb{R}^{3}$ be an arbitrary embedded surface which is homeomorphic to a cylinder and has everywhere negative Gaussian curvature. By using a suitable version of the Gauss-Bonnet theorem, show that $S$ contains at most one closed geodesic. [If required, appropriate forms of the Jordan curve theorem in the plane may also be used without proof.

  comment

• Paper 2, Section II, G

  Differential Geometry

  Part II, 2015

  If $U$ denotes a domain in $\mathbb{R}^{2}$, what is meant by saying that a smooth map $\phi: U \rightarrow \mathbb{R}^{3}$ is an immersion? Define what it means for such an immersion to be isothermal. Explain what it means to say that an immersed surface is minimal.

  Let $\phi(u, v)=(x(u, v), y(u, v), z(u, v))$ be an isothermal immersion. Show that it is minimal if and only if $x, y, z$ are harmonic functions of $u, v$. [You may use the formula for the mean curvature given in terms of the first and second fundamental forms, namely $\left.H=(e G-2 f F+g E) /\left(2\left\{E G-F^{2}\right\}\right) .\right]$

  Produce an example of an immersed minimal surface which is not an open subset of a catenoid, helicoid, or a plane. Prove that your example does give an immersed minimal surface in $\mathbb{R}^{3}$.

  comment

• Paper 3, Section II, H

  Algebraic Topology

  Part II, 2015

  Let $K$ and $L$ be simplicial complexes. Explain what is meant by a simplicial approximation to a continuous map $f:|K| \rightarrow|L|$. State the simplicial approximation theorem, and define the homomorphism induced on homology by a continuous map between triangulable spaces. [You do not need to show that the homomorphism is welldefined.]

  Let $h: S^{1} \rightarrow S^{1}$ be given by $z \mapsto z^{n}$ for a positive integer $n$, where $S^{1}$ is considered as the unit complex numbers. Compute the map induced by $h$ on homology.

  comment

• Paper 1, Section II, $22 G$

  Differential Geometry

  Part II, 2015

  Let $\Omega \subset \mathbb{R}^{2}$ be a domain (connected open subset) with boundary $\partial \Omega$ a continuously differentiable simple closed curve. Denoting by $A(\Omega)$ the area of $\Omega$ and $l(\partial \Omega)$ the length of the curve $\partial \Omega$, state and prove the isoperimetric inequality relating $A(\Omega)$ and $l(\partial \Omega)$ with optimal constant, including the characterization for equality. [You may appeal to Wirtinger's inequality as long as you state it precisely.]

  Does the result continue to hold if the boundary $\partial \Omega$ is allowed finitely many points at which it is not differentiable? Briefly justify your answer by giving either a counterexample or an indication of a proof.

  comment

• Paper 4, Section II, B

  Dynamical Systems

  Part II, 2015

  Let $f: I \rightarrow I$ be a continuous one-dimensional map of an interval $I \subset \mathbb{R}$. Explain what is meant by the statements (i) that $f$ has a horseshoe and (ii) that $f$ is chaotic (according to Glendinning's definition).

  Assume that $f$ has a 3-cycle $\left\{x_{0}, x_{1}, x_{2}\right\}$ with $x_{1}=f\left(x_{0}\right), x_{2}=f\left(x_{1}\right), x_{0}=f\left(x_{2}\right)$ and, without loss of generality, $x_{0}<x_{1}<x_{2}$. Prove that $f^{2}$ has a horseshoe. [You may assume the intermediate value theorem.]

  Represent the effect of $f$ on the intervals $I_{a}=\left[x_{0}, x_{1}\right]$ and $I_{b}=\left[x_{1}, x_{2}\right]$ by means of a directed graph, explaining carefully how the graph is constructed. Explain what feature of the graph implies the existence of a 3-cycle.

  The map $g: I \rightarrow I$ has a 5-cycle $\left\{x_{0}, x_{1}, x_{2}, x_{3}, x_{4}\right\}$ with $x_{i+1}=g\left(x_{i}\right), 0 \leqslant i \leqslant 3$ and $x_{0}=g\left(x_{4}\right)$, and $x_{0}<x_{1}<x_{2}<x_{3}<x_{4}$. For which $n, 1 \leqslant n \leqslant 4$, is an $n$-cycle of $g$ guaranteed to exist? Is $g$ guaranteed to be chaotic? Is $g$ guaranteed to have a horseshoe? Justify your answers. [You may use a suitable directed graph as part of your arguments.]

  How do your answers to the above change if instead $x_{4}<x_{2}<x_{1}<x_{3}<x_{0}$ ?

  comment

• Paper 3, Section II, B

  Dynamical Systems

  Part II, 2015

  Consider the dynamical system

  $$\begin{aligned} &\dot{x}=-\mu+x^{2}-y \\ &\dot{y}=y(a-x) \end{aligned}$$

  where $a$ is to be regarded as a fixed real constant and $\mu$ as a real parameter.

  Find the fixed points of the system and determine the stability of the system linearized about the fixed points. Hence identify the values of $\mu$ at given $a$ where bifurcations occur.

  Describe informally the concepts of centre manifold theory and apply it to analyse the bifurcations that occur in the above system with $a=1$. In particular, for each bifurcation derive an equation for the dynamics on the extended centre manifold and hence classify the bifurcation.

  What can you say, without further detailed calculation, about the case $a=0$ ?

  comment

• Paper 2, Section II, B

  Dynamical Systems

  Part II, 2015

  (a) An autonomous dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{2}$ has a periodic orbit $\mathbf{x}=\mathbf{X}(t)$ with period $T$. The linearized evolution of a small perturbation $\mathbf{x}=\mathbf{X}(t)+\boldsymbol{\eta}(t)$ is given by $\eta_{i}(t)=\Phi_{i j}(t) \eta_{j}(0)$. Obtain the differential equation and initial condition satisfied by the matrix $\Phi(t)$.

  Define the Floquet multipliers of the orbit. Explain why one of the multipliers is always unity and give a brief argument to show that the other is given by

  $$\exp \left(\int_{0}^{T} \nabla \cdot \mathbf{f}(\mathbf{X}(t)) d t\right)$$

  (b) Use the energy-balance method for nearly Hamiltonian systems to find leading-order approximations to the two limit cycles of the equation

  $$\ddot{x}+\epsilon\left(2 \dot{x}^{3}+2 x^{3}-4 x^{4} \dot{x}-\dot{x}\right)+x=0$$

  where $0<\epsilon \ll 1$.

  Determine the stability of each limit cycle, giving reasoning where necessary.

  [You may assume that $\int_{0}^{2 \pi} \cos ^{4} \theta d \theta=3 \pi / 4$ and $\int_{0}^{2 \pi} \cos ^{6} \theta d \theta=5 \pi / 8$.]

  comment

• Paper 1, Section II, 28B

  Dynamical Systems

  Part II, 2015

  (a) What is a Lyapunov function?

  Consider the dynamical system for $\mathbf{x}(t)=(x(t), y(t))$ given by

  $$\begin{aligned} &\dot{x}=-x+y+x\left(x^{2}+y^{2}\right) \\ &\dot{y}=-y-2 x+y\left(x^{2}+y^{2}\right) \end{aligned}$$

  Prove that the origin is asymptotically stable (quoting carefully any standard results that you use).

  Show that the domain of attraction of the origin includes the region $x^{2}+y^{2}<r_{1}^{2}$ where the maximum possible value of $r_{1}$ is to be determined.

  Show also that there is a region $E=\left\{\mathbf{x} \mid x^{2}+y^{2}>r_{2}^{2}\right\}$ such that $\mathbf{x}(0) \in E$ implies that $|\mathbf{x}(t)|$ increases without bound. Explain your reasoning carefully. Find the smallest possible value of $r_{2}$.

  (b) Now consider the dynamical system

  $$\begin{aligned} \dot{x} &=x-y-x\left(x^{2}+y^{2}\right) \\ \dot{y} &=y+2 x-y\left(x^{2}+y^{2}\right) \end{aligned}$$

  Prove that this system has a periodic solution (again, quoting carefully any standard results that you use).

  Demonstrate that this periodic solution is unique.

  comment

• Paper 4, Section II, A

  Electrodynamics

  Part II, 2015

  A point particle of charge $q$ has trajectory $y^{\mu}(\tau)$ in Minkowski space, where $\tau$ is its proper time. The resulting electromagnetic field is given by the Liénard-Wiechert 4-potential

  $$A^{\mu}(x)=-\frac{q \mu_{0} c}{4 \pi} \frac{u^{\mu}\left(\tau_{*}\right)}{R^{\nu}\left(\tau_{*}\right) u_{\nu}\left(\tau_{*}\right)}, \quad \text { where } \quad R^{\nu}=x^{\nu}-y^{\nu}(\tau) \quad \text { and } \quad u^{\mu}=d y^{\mu} / d \tau$$

  Write down the condition that determines the point $y^{\mu}\left(\tau_{*}\right)$ on the trajectory of the particle for a given value of $x^{\mu}$. Express this condition in terms of components, setting $x^{\mu}=(c t, \mathbf{x})$ and $y^{\mu}=\left(c t^{\prime}, \mathbf{y}\right)$, and define the retarded time $t_{r}$.

  Suppose that the 3 -velocity of the particle $\mathbf{v}\left(t^{\prime}\right)=\dot{\mathbf{y}}\left(t^{\prime}\right)=d \mathbf{y} / d t^{\prime}$ is small in size compared to $c$, and suppose also that $r=|\mathbf{x}| \gg|\mathbf{y}|$. Working to leading order in $1 / r$ and to first order in $\mathbf{v}$, show that

  $$\phi(x)=\frac{q \mu_{0} c}{4 \pi r}\left(c+\hat{\mathbf{r}} \cdot \mathbf{v}\left(t_{r}\right)\right), \quad \mathbf{A}(x)=\frac{q \mu_{0}}{4 \pi r} \mathbf{v}\left(t_{r}\right), \quad \text { where } \quad \hat{\mathbf{r}}=\mathbf{x} / r$$

  Now assume that $t_{r}$ can be replaced by $t_{-}=t-(r / c)$ in the expressions for $\phi$ and $\mathbf{A}$ above. Calculate the electric and magnetic fields to leading order in $1 / r$ and hence show that the Poynting vector is (in this approximation)

  $$\mathbf{N}(x)=\frac{q^{2} \mu_{0}}{(4 \pi)^{2} c} \frac{\hat{\mathbf{r}}}{r^{2}}\left|\hat{\mathbf{r}} \times \dot{\mathbf{v}}\left(t_{-}\right)\right|^{2}$$

  If the charge $q$ is performing simple harmonic motion $\mathbf{y}\left(t^{\prime}\right)=A \mathbf{n} \cos \omega t^{\prime}$, where $\mathbf{n}$ is a unit vector and $A \omega \ll c$, find the total energy radiated during one period of oscillation.

  comment

• Paper 3, Section II, 34A

  Electrodynamics

  Part II, 2015

  (i) Consider the action

  $$S=-\frac{1}{4 \mu_{0} c} \int\left(F_{\mu \nu} F^{\mu \nu}+2 \lambda^{2} A_{\mu} A^{\mu}\right) d^{4} x+\frac{1}{c} \int A_{\mu} J^{\mu} d^{4} x$$

  where $A_{\mu}(x)$ is a 4-vector potential, $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$ is the field strength tensor, $J^{\mu}(x)$ is a conserved current, and $\lambda \geqslant 0$ is a constant. Derive the field equation

  $$\partial_{\mu} F^{\mu \nu}-\lambda^{2} A^{\nu}=-\mu_{0} J^{\nu} .$$

  For $\lambda=0$ the action $S$ describes standard electromagnetism. Show that in this case the theory is invariant under gauge transformations of the field $A_{\mu}(x)$, which you should define. Is the theory invariant under these same gauge transformations when $\lambda>0$ ?

  Show that when $\lambda>0$ the field equation above implies

  $$\partial_{\mu} \partial^{\mu} A^{\nu}-\lambda^{2} A^{\nu}=-\mu_{0} J^{\nu}$$

  Under what circumstances does $(*)$ hold in the case $\lambda=0$ ?

  (ii) Now suppose that $A_{\mu}(x)$ and $J_{\mu}(x)$ obeying $(*)$ reduce to static 3 -vectors $\mathbf{A}(\mathbf{x})$ and $\mathbf{J}(\mathbf{x})$ in some inertial frame. Show that there is a solution

  $$\mathbf{A}(\mathbf{x})=-\mu_{0} \int G\left(\left|\mathbf{x}-\mathbf{x}^{\prime}\right|\right) \mathbf{J}\left(\mathbf{x}^{\prime}\right) d^{3} \mathbf{x}^{\prime}$$

  for a suitable Green's function $G(R)$ with $G(R) \rightarrow 0$ as $R \rightarrow \infty$. Determine $G(R)$ for any $\lambda \geqslant 0$. [Hint: You may find it helpful to consider first the case $\lambda=0$ and then the case $\lambda>0$, using the result $\nabla^{2}\left(\frac{1}{R} f(R)\right)=\nabla^{2}\left(\frac{1}{R}\right) f(R)+\frac{1}{R} f^{\prime \prime}(R)$, where $\left.R=\left|\mathbf{x}-\mathbf{x}^{\prime}\right| .\right]$

  If $\mathbf{J}(\mathbf{x})$ is zero outside some bounded region, comment on the effect of the value of $\lambda$ on the behaviour of $\mathbf{A}(\mathbf{x})$ when $|\mathbf{x}|$ is large. [No further detailed calculations are required.]

  comment

• Paper 1, Section II, A

  Electrodynamics

  Part II, 2015

  Briefly explain how to interpret the components of the relativistic stress-energy tensor in terms of the density and flux of energy and momentum in some inertial frame.

  (i) The stress-energy tensor of the electromagnetic field is

  $$T_{\mathrm{em}}^{\mu \nu}=\frac{1}{\mu_{0}}\left(F^{\mu \alpha} F_{\alpha}^{\nu}-\frac{1}{4} \eta^{\mu \nu} F^{\alpha \beta} F_{\alpha \beta}\right)$$

  where $F_{\mu \nu}$ is the field strength, $\eta_{\mu \nu}$ is the Minkowski metric, and $\mu_{0}$ is the permeability of free space. Show that $\partial_{\mu} T_{\mathrm{em}}^{\mu \nu}=-F_{\mu}^{\nu} J^{\mu}$, where $J^{\mu}$ is the current 4-vector.

  [ Maxwell's equations are $\partial_{\mu} F^{\mu \nu}=-\mu_{0} J^{\nu}$ and $\partial_{\rho} F_{\mu \nu}+\partial_{\nu} F_{\rho \mu}+\partial_{\mu} F_{\nu \rho}=0 .$ ]

  (ii) A fluid consists of point particles of rest mass $m$ and charge $q$. The fluid can be regarded as a continuum, with 4 -velocity $u^{\mu}(x)$ depending on the position $x$ in spacetime. For each $x$ there is an inertial frame $S_{x}$ in which the fluid particles at $x$ are at rest. By considering components in $S_{x}$, show that the fluid has a current 4-vector field

  $$J^{\mu}=q n_{0} u^{\mu}$$

  and a stress-energy tensor

  $$T_{\text {fluid }}^{\mu \nu}=m n_{0} u^{\mu} u^{\nu},$$

  where $n_{0}(x)$ is the proper number density of particles (the number of particles per unit spatial volume in $S_{x}$ in a small region around $x$ ). Write down the Lorentz 4-force on a fluid particle at $x$. By considering the resulting 4 -acceleration of the fluid, show that the total stress-energy tensor is conserved, i.e.

  $$\partial_{\mu}\left(T_{\mathrm{em}}^{\mu \nu}+T_{\text {fluid }}^{\mu \nu}\right)=0 .$$

  comment

• Paper 4, Section II, E

  Fluid Dynamics II

  Part II, 2015

  A stationary inviscid fluid of thickness $h$ and density $\rho$ is located below a free surface at $y=h$ and above a deep layer of inviscid fluid of the same density in $y<0$ flowing with uniform velocity $U>0$ in the $\mathbf{e}_{x}$ direction. The base velocity profile is thus

  $$u=U, y<0 ; \quad u=0,0<y<h$$

  while the free surface at $y=h$ is maintained flat by gravity.

  By considering small perturbations of the vortex sheet at $y=0$ of the form $\eta=\eta_{0} e^{i k x+\sigma t}, k>0$, calculate the dispersion relationship between $k$ and $\sigma$ in the irrotational limit. By explicitly deriving that

  $$\operatorname{Re}(\sigma)=\pm \frac{\sqrt{\tanh (h k)}}{1+\tanh (h k)} U k$$

  deduce that the vortex sheet is unstable at all wavelengths. Show that the growth rates of the unstable modes are approximately $U k / 2$ when $h k \gg 1$ and $U k \sqrt{h k}$ when $h k \ll 1$.

  comment

• Paper 2, Section II, E

  Fluid Dynamics II

  Part II, 2015

  Consider an infinite rigid cylinder of radius a parallel to a horizontal rigid stationary surface. Let $\mathbf{e}_{x}$ be the direction along the surface perpendicular to the cylinder axis, $\mathbf{e}_{y}$ the direction normal to the surface (the surface is at $y=0$ ) and $\mathbf{e}_{z}$ the direction along the axis of the cylinder. The cylinder moves with constant velocity $U \mathbf{e}_{x}$. The minimum separation between the cylinder and the surface is denoted by $h_{0} \ll a$.

  (i) What are the conditions for the flow in the thin gap between the cylinder and the surface to be described by the lubrication equations? State carefully the relevant length scale in the $\mathbf{e}_{x}$ direction.

  (ii) Without doing any calculation, explain carefully why, in the lubrication limit, the net fluid force $\mathbf{F}$ acting on the stationary surface at $y=0$ has no component in the $\mathbf{e}_{y}$ direction.

  (iii) Using the lubrication approximation, calculate the $\mathbf{e}_{x}$ component of the velocity field in the gap between the cylinder and the surface, and determine the pressure gradient as a function of the gap thickness $h(x)$.

  (iv) Compute the tangential component of the force, $\mathbf{e}_{x} \cdot \mathbf{F}$, acting on the bottom surface per unit length in the $\mathbf{e}_{z}$ direction.

  [You may quote the following integrals:

  $$\int_{-\infty}^{\infty} \frac{d u}{\left(1+u^{2}\right)}=\pi, \quad \int_{-\infty}^{\infty} \frac{d u}{\left(1+u^{2}\right)^{2}}=\frac{\pi}{2}, \quad \int_{-\infty}^{\infty} \frac{d u}{\left(1+u^{2}\right)^{3}}=\frac{3 \pi}{8}$$

  comment

• Paper 4, Section II, H

  Algebraic Topology

  Part II, 2015

  State the Mayer-Vietoris theorem for a simplicial complex $K$ which is the union of two subcomplexes $M$ and $N$. Explain briefly how the connecting homomorphism $\partial_{n}: H_{n}(K) \rightarrow H_{n-1}(M \cap N)$ is defined.

  If $K$ is the union of subcomplexes $M_{1}, M_{2}, \ldots, M_{n}$, with $n \geqslant 2$, such that each intersection

  $$M_{i_{1}} \cap M_{i_{2}} \cap \cdots \cap M_{i_{k}}, \quad 1 \leqslant k \leqslant n,$$

  is either empty or has the homology of a point, then show that

  $$H_{i}(K)=0 \quad \text { for } \quad i \geqslant n-1 .$$

  Construct examples for each $n \geqslant 2$ showing that this is sharp.

  comment

• Paper 3, Section II, E

  Fluid Dynamics II

  Part II, 2015

  Consider a three-dimensional high-Reynolds number jet without swirl induced by a force $\mathbf{F}=F \mathbf{e}_{z}$ imposed at the origin in a fluid at rest. The velocity in the jet, described using cylindrical coordinates $(r, \theta, z)$, is assumed to remain steady and axisymmetric, and described by a boundary layer analysis.

  (i) Explain briefly why the flow in the jet can be described by the boundary layer equations

  $$u_{r} \frac{\partial u_{z}}{\partial r}+u_{z} \frac{\partial u_{z}}{\partial z}=\nu \frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial u_{z}}{\partial r}\right)$$

  (ii) Show that the momentum flux in the jet, $F=\int_{S} \rho u_{z}^{2} d S$, where $S$ is an infinite surface perpendicular to $\mathbf{e}_{z}$, is not a function of $z$. Combining this result with scalings from the boundary layer equations, derive the scalings for the unknown width $\delta(z)$ and typical velocity $U(z)$ of the jet as functions of $z$ and the other parameters of the problem $(\rho, \nu, F)$.

  (iii) Solving for the flow using a self-similar Stokes streamfunction

  $$\psi(r, z)=U(z) \delta^{2}(z) f(\eta), \quad \eta=r / \delta(z)$$

  show that $f(\eta)$ satisfies the differential equation

  $$f f^{\prime}-\eta\left(f^{\prime 2}+f f^{\prime \prime}\right)=f^{\prime}-\eta f^{\prime \prime}+\eta^{2} f^{\prime \prime \prime} .$$

  What boundary conditions should be applied to this equation? Give physical reasons for them.

  [Hint: In cylindrical coordinates for axisymmetric incompressible flow $\left(u_{r}(r, z), 0, u_{z}(r, z)\right)$ you are given the incompressibility condition as

  $$\frac{1}{r} \frac{\partial}{\partial r}\left(r u_{r}\right)+\frac{\partial u_{z}}{\partial z}=0$$

  the $z$-component of the Navier-Stokes equation as

  $$\rho\left(\frac{\partial u_{z}}{\partial t}+u_{r} \frac{\partial u_{z}}{\partial r}+u_{z} \frac{\partial u_{z}}{\partial z}\right)=-\frac{\partial p}{\partial z}+\mu\left[\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial u_{z}}{\partial r}\right)+\frac{\partial^{2} u_{z}}{\partial z^{2}}\right]$$

  and the relationship between the Stokes streamfunction, $\psi(r, z)$, and the velocity components as

  $$\left.u_{r}=-\frac{1}{r} \frac{\partial \psi}{\partial z}, \quad u_{z}=\frac{1}{r} \frac{\partial \psi}{\partial r}\right]$$

  comment

• Paper 1, Section II, E

  Fluid Dynamics II

  Part II, 2015

  (i) In a Newtonian fluid, the deviatoric stress tensor is linearly related to the velocity gradient so that the total stress tensor is

  $$\sigma_{i j}=-p \delta_{i j}+A_{i j k l} \frac{\partial u_{k}}{\partial x_{l}}$$

  Show that for an incompressible isotropic fluid with a symmetric stress tensor we necessarily have

  $$A_{i j k l} \frac{\partial u_{k}}{\partial x_{l}}=2 \mu e_{i j} \text {, }$$

  where $\mu$ is a constant which we call the dynamic viscosity and $e_{i j}$ is the symmetric part of $\partial u_{i} / \partial x_{j}$.

  (ii) Consider Stokes flow due to the translation of a rigid sphere $S_{a}$ of radius $a$ so that the sphere exerts a force $\mathbf{F}$ on the fluid. At distances much larger than the radius of the sphere, the instantaneous velocity and pressure fields are

  $$u_{i}(\mathbf{x})=\frac{1}{8 \mu \pi}\left(\frac{F_{i}}{r}+\frac{F_{m} x_{m} x_{i}}{r^{3}}\right), \quad p(\mathbf{x})=\frac{1}{4 \pi} \frac{F_{m} x_{m}}{r^{3}},$$

  where $\mathbf{x}$ is measured with respect to an origin located at the centre of the sphere, and $r=|\mathbf{x}|$.

  Consider a sphere $S_{R}$ of radius $R \gg a$ instantaneously concentric with $S_{a}$. By explicitly computing the tractions and integrating them, show that the force $G$ exerted by the fluid located in $r>R$ on $S_{R}$ is constant and independent of $R$, and evaluate it.

  (iii) Explain why the Stokes equations in the absence of body forces can be written

  $$\frac{\partial \sigma_{i j}}{\partial x_{j}}=0$$

  Show that by integrating this equation in the fluid volume located instantaneously between $S_{a}$ and $S_{R}$, you can recover the result in (ii) directly.

  comment

• Paper 4, Section I, B

  Further Complex Methods

  Part II, 2015

  Explain how the Papperitz symbol

  $$P\left\{\begin{array}{cccc} z_{1} & z_{2} & z_{3} & \\ \alpha_{1} & \beta_{1} & \gamma_{1} & z \\ \alpha_{2} & \beta_{2} & \gamma_{2} & \end{array}\right\}$$

  represents a differential equation with certain properties. [You need not write down the differential equation explicitly.]

  The hypergeometric function $F(a, b, c ; z)$ is defined to be the solution of the equation given by the Papperitz symbol

  

  that is analytic at $z=0$ and such that $F(a, b, c ; 0)=1$. Show that

  $$F(a, b, c ; z)=(1-z)^{-a} F\left(a, c-b, c ; \frac{z}{z-1}\right) \text {, }$$

  indicating clearly any general results for manipulating Papperitz symbols that you use.

  comment

• Paper 3, Section $I$, B

  Further Complex Methods

  Part II, 2015

  Define what is meant by the Cauchy principal value in the particular case

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{\cos x}{x^{2}-a^{2}} d x$$

  where the constant $a$ is real and strictly positive. Evaluate this expression explicitly, stating clearly any standard results involving contour integrals that you use.

  comment

• Paper 2, Section I, B

  Further Complex Methods

  Part II, 2015

  Give a brief description of what is meant by analytic continuation.

  The dilogarithm function is defined by

  $$\mathrm{Li}_{2}(z)=\sum_{n=1}^{\infty} \frac{z^{n}}{n^{2}}, \quad|z|<1$$

  Let

  $$f(z)=-\int_{C} \frac{1}{u} \ln (1-u) d u$$

  where $C$ is a contour that runs from the origin to the point $z$. Show that $f(z)$ provides an analytic continuation of $\mathrm{Li}_{2}(z)$ and describe its domain of definition in the complex plane, given a suitable branch cut.

  comment

• Paper 1, Section $I$, B

  Further Complex Methods

  Part II, 2015

  Evaluate the real integral

  $$\int_{0}^{\infty} \frac{x^{1 / 2} \ln x}{1+x^{2}} d x$$

  where $x^{1 / 2}$ is taken to be the positive square root.

  What is the value of

  $$\int_{0}^{\infty} \frac{x^{1 / 2}}{1+x^{2}} d x ?$$

  comment

• Paper 2, Section II, B

  Further Complex Methods

  Part II, 2015

  The Riemann zeta function is defined by the sum

  $$\zeta(s)=\sum_{n=1}^{\infty} n^{-s}$$

  which converges for $\operatorname{Re} s>1$. Show that

  $$\zeta(s)=\frac{1}{\Gamma(s)} \int_{0}^{\infty} \frac{t^{s-1}}{e^{t}-1} d t, \quad \operatorname{Re} s>1$$

  The analytic continuation of $\zeta(s)$ is given by the Hankel contour integral

  $$\zeta(s)=\frac{\Gamma(1-s)}{2 \pi i} \int_{-\infty}^{0+} \frac{t^{s-1}}{e^{-t}-1} d t$$

  Verify that this agrees with the integral $(*)$ above when Re $s>1$ and $s$ is not an integer. [You may assume $\Gamma(s) \Gamma(1-s)=\pi / \sin \pi s$.] What happens when $s=2,3,4, \ldots$ ?

  Evaluate $\zeta(0)$. Show that $\left(e^{-t}-1\right)^{-1}+\frac{1}{2}$ is an odd function of $t$ and hence, or otherwise, show that $\zeta(-2 n)=0$ for any positive integer $n$.

  comment

• Paper 1, Section II, B

  Further Complex Methods

  Part II, 2015

  Consider the differential equation

  $$x y^{\prime \prime}+(a-x) y^{\prime}-b y=0$$

  where $a$ and $b$ are constants with $\operatorname{Re}(b)>0$ and $\operatorname{Re}(a-b)>0$. Laplace's method for finding solutions involves writing

  $$y(x)=\int_{C} e^{x t} f(t) d t$$

  for some suitable contour $C$ and some suitable function $f(t)$. Determine $f(t)$ for the equation $(*)$ and use a clearly labelled diagram to specify contours $C$ giving two independent solutions when $x$ is real in each of the cases $x>0$ and $x<0$.

  Now let $a=3$ and $b=1$. Find explicit expressions for two independent solutions to $(*)$. Find, in addition, a solution $y(x)$ with $y(0)=1$.

  comment

• Paper 3, Section II, F

  Galois Theory

  Part II, 2015

  Let $f \in \mathbb{Q}[t]$ be of degree $n>0$, with no repeated roots, and let $L$ be a splitting field for $f$.

  (i) Show that $f$ is irreducible if and only if for any $\alpha, \beta \in \operatorname{Root}_{f}(L)$ there is $\phi \in \operatorname{Gal}(L / \mathbb{Q})$ such that $\phi(\alpha)=\beta$.

  (ii) Explain how to define an injective homomorphism $\tau: \operatorname{Gal}(L / \mathbb{Q}) \rightarrow S_{n}$. Find an example in which the image of $\tau$ is the subgroup of $S_{3}$ generated by (2 3). Find another example in which $\tau$ is an isomorphism onto $S_{3}$.

  (iii) Let $f(t)=t^{5}-3$ and assume $f$ is irreducible. Find a chain of subgroups of $\operatorname{Gal}(L / \mathbb{Q})$ that shows it is a solvable group. [You may quote without proof any theorems from the course, provided you state them clearly.]

  comment

• Paper 4, Section II, $17 \mathrm{~F}$

  Galois Theory

  Part II, 2015

  (i) Prove that a finite solvable extension $K \subseteq L$ of fields of characteristic zero is a radical extension.

  (ii) Let $x_{1}, \ldots, x_{7}$ be variables, $L=\mathbb{Q}\left(x_{1}, \ldots, x_{7}\right)$, and $K=\mathbb{Q}\left(e_{1}, \ldots, e_{7}\right)$ where $e_{i}$ are the elementary symmetric polynomials in the variables $x_{i}$. Is there an element $\alpha \in L$ such that $\alpha^{2} \in K$ but $\alpha \notin K$ ? Justify your answer.

  (iii) Find an example of a field extension $K \subseteq L$ of degree two such that $L \neq K(\sqrt{\alpha})$ for any $\alpha \in K$. Give an example of a field which has no extension containing an $11 t h$ primitive root of unity.

  comment

• Paper 2, Section II, H

  Algebraic Topology

  Part II, 2015

  Define what it means for $p: \widetilde{X} \rightarrow X$ to be a covering map, and what it means to say that $p$ is a universal cover.

  Let $p: \tilde{X} \rightarrow X$ be a universal cover, $A \subset X$ be a locally path connected subspace, and $\tilde{A} \subset p^{-1}(A)$ be a path component containing a point $\tilde{a}_{0}$ with $p\left(\tilde{a}_{0}\right)=a_{0}$. Show that the restriction $\left.p\right|_{\tilde{A}}: \widetilde{A} \rightarrow A$ is a covering map, and that under the Galois correspondence it corresponds to the subgroup

  $$\operatorname{Ker}\left(\pi_{1}\left(A, a_{0}\right) \rightarrow \pi_{1}\left(X, a_{0}\right)\right)$$

  of $\pi_{1}\left(A, a_{0}\right)$.

  comment

• Paper 2, Section II, F

  Galois Theory

  Part II, 2015

  (i) State the fundamental theorem of Galois theory, without proof. Let $L$ be a splitting field of $t^{3}-2 \in \mathbb{Q}[t]$. Show that $\mathbb{Q} \subseteq L$ is Galois and that Gal $(L / \mathbb{Q})$ has a subgroup which is not normal.

  (ii) Let $\Phi_{8}$ be the 8 th cyclotomic polynomial and denote its image in $\mathbb{F}_{7}[t]$ again by $\Phi_{8}$. Show that $\Phi_{8}$ is not irreducible in $\mathbb{F}_{7}[t]$.

  (iii) Let $m$ and $n$ be coprime natural numbers, and let $\mu_{m}=\exp (2 \pi i / m)$ and $\mu_{n}=\exp (2 \pi i / n)$ where $i=\sqrt{-1}$. Show that $\mathbb{Q}\left(\mu_{m}\right) \cap \mathbb{Q}\left(\mu_{n}\right)=\mathbb{Q}$.

  comment

• Paper 1, Section II, $17 \mathrm{~F}$

  Galois Theory

  Part II, 2015

  (i) Let $K \subseteq L$ be a field extension and $f \in K[t]$ be irreducible of positive degree. Prove the theorem which states that there is a $1-1$ correspondence

  $$\operatorname{Root}_{f}(L) \longleftrightarrow \operatorname{Hom}_{K}\left(\frac{K[t]}{\langle f\rangle}, L\right)$$

  (ii) Let $K$ be a field and $f \in K[t]$. What is a splitting field for $f$ ? What does it mean to say $f$ is separable? Show that every $f \in K[t]$ is separable if $K$ is a finite field.

  (iii) The primitive element theorem states that if $K \subseteq L$ is a finite separable field extension, then $L=K(\alpha)$ for some $\alpha \in L$. Give the proof of this theorem assuming $K$ is infinite.

  comment

• Paper 4, Section II, D

  General Relativity

  Part II, 2015

  In static spherically symmetric coordinates, the metric $g_{a b}$ for de Sitter space is given by

  $$d s^{2}=-\left(1-r^{2} / a^{2}\right) d t^{2}+\left(1-r^{2} / a^{2}\right)^{-1} d r^{2}+r^{2} d \Omega^{2}$$

  where $d \Omega^{2}=d \theta^{2}+\sin ^{2} \theta d \phi^{2}$ and $a$ is a constant.

  (a) Let $u=t-a \tanh ^{-1}(r / a)$ for $r \leqslant a$. Use the $(u, r, \theta, \phi)$ coordinates to show that the surface $r=a$ is non-singular. Is $r=0$ a space-time singularity?

  (b) Show that the vector field $g^{a b} u_{, a}$ is null.

  (c) Show that the radial null geodesics must obey either

  $$\frac{d u}{d r}=0 \quad \text { or } \quad \frac{d u}{d r}=-\frac{2}{1-r^{2} / a^{2}}$$

  Which of these families of geodesics is outgoing $(d r / d t>0) ?$

  Sketch these geodesics in the $(u, r)$ plane for $0 \leqslant r \leqslant a$, where the $r$-axis is horizontal and lines of constant $u$ are inclined at $45^{\circ}$ to the horizontal.

  (d) Show, by giving an explicit example, that an observer moving on a timelike geodesic starting at $r=0$ can cross the surface $r=a$ within a finite proper time.

  comment

• Paper 2, Section II, D

  General Relativity

  Part II, 2015

  (a) The Schwarzschild metric is

  $$d s^{2}=-\left(1-r_{s} / r\right) d t^{2}+\left(1-r_{s} / r\right)^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  (in units for which the speed of light $c=1$ ). Show that a timelike geodesic in the equatorial plane obeys

  $$\frac{1}{2} \dot{r}^{2}+V(r)=\frac{1}{2} E^{2}$$

  where

  $$2 V(r)=\left(1-\frac{r_{s}}{r}\right)\left(1+\frac{h^{2}}{r^{2}}\right)$$

  and $E$ and $h$ are constants.

  (b) For a circular orbit of radius $r$, show that

  $$h^{2}=\frac{r^{2} r_{s}}{2 r-3 r_{s}} .$$

  Given that the orbit is stable, show that $r>3 r_{s}$.

  (c) Alice lives on a small planet that is in a stable circular orbit of radius $r$ around a (non-rotating) black hole of radius $r_{s}$. Bob lives on a spacecraft in deep space far from the black hole and at rest relative to it. Bob is ageing $k$ times faster than Alice. Find an expression for $k^{2}$ in terms of $r$ and $r_{s}$ and show that $k<\sqrt{2}$.

  comment

• Paper 3, Section II, D

  General Relativity

  Part II, 2015

  Let $\Gamma_{b c}^{a}$ be the Levi-Civita connection and $R_{b c d}^{a}$ the Riemann tensor corresponding to a metric $g_{a b}(x)$, and let $\widetilde{\Gamma}_{b c}^{a}$ be the Levi-Civita connection and $\widetilde{R}_{b c d}^{a}$ the Riemann tensor corresponding to a metric $\tilde{g}_{a b}(x)$. Let $T_{b c}^{a}=\widetilde{\Gamma}_{b c}^{a}-\Gamma_{b c}^{a}$.

  (a) Show that $T_{b c}^{a}$ is a tensor.

  (b) Using local inertial coordinates for the metric $g_{a b}$, or otherwise, show that

  $$\widetilde{R}_{b c d}^{a}-R_{b c d}^{a}=2 T_{b[d ; c]}^{a}-2 T_{e[d}^{a} T_{c] b}^{e}$$

  holds in all coordinate systems, where the semi-colon denotes covariant differentiation using the connection $\Gamma_{b c}^{a}$. [You may assume that $R_{b c d}^{a}=2 \Gamma_{b[d, c]}^{a}-2 \Gamma_{e[d}^{a} \Gamma_{c] b}^{e}$.]

  (c) In the case that $T_{b c}^{a}=\ell^{a} g_{b c}$ for some vector field $\ell^{a}$, show that $\widetilde{R}_{b d}=R_{b d}$ if and only if

  $$\ell_{b ; d}+\ell_{b} \ell_{d}=0$$

  (d) Using the result that $\ell_{[a ; b]}=0$ if and only if $\ell_{a}=\phi_{, a}$ for some scalar field $\phi$, show that the condition on $\ell_{a}$ in part (c) can be written as

  $$k_{a ; b}=0$$

  for a certain covector field $k_{a}$, which you should define.

  comment

• Paper 1, Section II, 35D

  General Relativity

  Part II, 2015

  A vector field $\xi^{a}$ is said to be a conformal Killing vector field of the metric $g_{a b}$ if

  $$\xi_{(a ; b)}=\frac{1}{2} \psi g_{a b}$$

  for some scalar field $\psi$. It is a Killing vector field if $\psi=0$.

  (a) Show that $(*)$ is equivalent to

  $$\xi^{c} g_{a b, c}+\xi_{, a}^{c} g_{b c}+\xi_{, b}^{c} g_{a c}=\psi g_{a b}$$

  (b) Show that if $\xi^{a}$ is a conformal Killing vector field of the metric $g_{a b}$, then $\xi^{a}$ is a Killing vector field of the metric $\mathrm{e}^{2 \phi} g_{a b}$, where $\phi$ is any function that obeys

  $$2 \xi^{c} \phi_{, c}+\psi=0 .$$

  (c) Use part (b) to find an example of a metric with coordinates $t, x, y$ and $z$ (where $t>0)$ for which $(t, x, y, z)$ are the contravariant components of a Killing vector field. [Hint: You may wish to start by considering what happens in Minkowski space.]

  comment

• Paper 1, Section II, I

  Graph Theory

  Part II, 2015

  (a) What does it mean to say that a graph $G$ is strongly regular with parameters $(k, a, b) ?$

  (b) Let $G$ be an incomplete, strongly regular graph with parameters $(k, a, b)$ and of order $n$. Suppose $b \geqslant 1$. Show that the numbers

  $$\frac{1}{2}\left(n-1 \pm \frac{(n-1)(b-a)-2 k}{\sqrt{(a-b)^{2}+4(k-b)}}\right)$$

  are integers.

  (c) Suppose now that $G$ is an incomplete, strongly regular graph with parameters $(k, 0,3)$. Show that $|G| \in\{6,162\}$.

  comment

• Paper 2, Section II, I

  Graph Theory

  Part II, 2015

  (a) Define the Ramsey numbers $R(s, t)$ and $R(s)$ for integers $s, t \geqslant 2$. Show that $R(s, t)$ exists for all $s, t \geqslant 2$ and that if $s, t \geqslant 3$ then $R(s, t) \leqslant R(s-1, t)+R(s, t-1)$.

  (b) Show that, as $s \rightarrow \infty$, we have $R(s)=O\left(4^{s}\right)$ and $R(s)=\Omega\left(2^{s / 2}\right)$.

  (c) Show that, as $t \rightarrow \infty$, we have $R(3, t)=O\left(t^{2}\right)$ and $R(3, t)=\Omega\left(\left(\frac{t}{\log t}\right)^{3 / 2}\right)$.

  [Hint: For the lower bound in (c), you may wish to begin by modifying a random graph to show that for all $n$ and $p$ we have

  $$R(3, t)>n-\left(\begin{array}{l} n \\ 3 \end{array}\right) p^{3}-\left(\begin{array}{c} n \\ t \end{array}\right)(1-p)\left(\begin{array}{c} t \\ 2 \end{array}\right)$$

  comment

• Paper 3, Section II, I

  Graph Theory

  Part II, 2015

  (a) Let $G$ be a graph. What is a Hamilton cycle in $G$ ? What does it mean to say that $G$ is Hamiltonian?

  (b) Let $G$ be a graph of order $n \geqslant 3$ satisfying $\delta(G) \geqslant \frac{n}{2}$. Show that $G$ is Hamiltonian. For each $n \geqslant 3$, exhibit a non-Hamiltonian graph $G_{n}$ of order $n$ with $\delta\left(G_{n}\right)=\left\lceil\frac{n}{2}\right\rceil-1$.

  (c) Let $H$ be a bipartite graph with $n \geqslant 2$ vertices in each class satisfying $\delta(H)>\frac{n}{2}$. Show that $H$ is Hamiltonian. For each $n \geqslant 2$, exhibit a non-Hamiltonian bipartite graph $H_{n}$ with $n$ vertices in each class and $\delta\left(H_{n}\right)=\left\lfloor\frac{n}{2}\right\rfloor$.

  comment

• Paper 4, Section II, I

  Graph Theory

  Part II, 2015

  Let $G$ be a bipartite graph with vertex classes $X$ and $Y$. What does it mean to say that $G$ contains a matching from $X$ to $Y$ ? State and prove Hall's Marriage Theorem.

  Suppose now that every $x \in X$ has $d(x) \geqslant 1$, and that if $x \in X$ and $y \in Y$ with $x y \in E(G)$ then $d(x) \geqslant d(y)$. Show that $G$ contains a matching from $X$ to $Y$.

  comment

• Paper 1, Section II, H

  Algebraic Topology

  Part II, 2015

  State carefully a version of the Seifert-van Kampen theorem for a cover of a space by two closed sets.

  Let $X$ be the space obtained by gluing together a Möbius band $M$ and a torus $T=S^{1} \times S^{1}$ along a homeomorphism of the boundary of $M$ with $S^{1} \times\{1\} \subset T$. Find a presentation for the fundamental group of $X$, and hence show that it is infinite and non-abelian.

  comment

• Paper 1, Section II, D

  Integrable Systems

  Part II, 2015

  Let $u_{t}=K\left(x, u, u_{x}, \ldots\right)$ be an evolution equation for the function $u=u(x, t)$. Assume $u$ and all its derivatives decay rapidly as $|x| \rightarrow \infty$. What does it mean to say that the evolution equation for $u$ can be written in Hamiltonian form?

  The modified KdV (mKdV) equation for $u$ is

  $$u_{t}+u_{x x x}-6 u^{2} u_{x}=0 .$$

  Show that small amplitude solutions to this equation are dispersive.

  Demonstrate that the mKdV equation can be written in Hamiltonian form and define the associated Poisson bracket $\{,$,} on the space of functionals of u. Verify that the Poisson bracket is linear in each argument and anti-symmetric.

  Show that a functional $I=I[u]$ is a first integral of the mKdV equation if and only if $\{I, H\}=0$, where $H=H[u]$ is the Hamiltonian.

  Show that if $u$ satisfies the mKdV equation then

  $$\frac{\partial}{\partial t}\left(u^{2}\right)+\frac{\partial}{\partial x}\left(2 u u_{x x}-u_{x}^{2}-3 u^{4}\right)=0$$

  Using this equation, show that the functional

  $$I[u]=\int u^{2} d x$$

  Poisson-commutes with the Hamiltonian.

  comment

• Paper 2, Section II, D

  Integrable Systems

  Part II, 2015

  (a) Explain how a vector field

  $$V=\xi(x, u) \frac{\partial}{\partial x}+\eta(x, u) \frac{\partial}{\partial u}$$

  generates a 1-parameter group of transformations $g^{\epsilon}:(x, u) \mapsto(\tilde{x}, \tilde{u})$ in terms of the solution to an appropriate differential equation. [You may assume the solution to the relevant equation exists and is unique.]

  (b) Suppose now that $u=u(x)$. Define what is meant by a Lie-point symmetry of the ordinary differential equation

  $$\Delta\left[x, u, u^{(1)}, \ldots, u^{(n)}\right]=0, \quad \text { where } \quad u^{(k)} \equiv \frac{d^{k} u}{d x^{k}}, \quad k=1, \ldots, n$$

  (c) Prove that every homogeneous, linear ordinary differential equation for $u=u(x)$ admits a Lie-point symmetry generated by the vector field

  $$V=u \frac{\partial}{\partial u}$$

  By introducing new coordinates

  $$s=s(x, u), \quad t=t(x, u)$$

  which satisfy $V(s)=1$ and $V(t)=0$, show that every differential equation of the form

  $$\frac{d^{2} u}{d x^{2}}+p(x) \frac{d u}{d x}+q(x) u=0$$

  can be reduced to a first-order differential equation for an appropriate function.

  comment

• Paper 3, Section II, D

  Integrable Systems

  Part II, 2015

  Let $L=L(t)$ and $A=A(t)$ be real $N \times N$ matrices, with $L$ symmetric and $A$ antisymmetric. Suppose that

  $$\frac{d L}{d t}=L A-A L$$

  Show that all eigenvalues of the matrix $L(t)$ are $t$-independent. Deduce that the coefficients of the polynomial

  $$P(x)=\operatorname{det}(x I-L(t))$$

  are first integrals of the system.

  What does it mean for a $2 n$-dimensional Hamiltonian system to be integrable? Consider the Toda system with coordinates $\left(q_{1}, q_{2}, q_{3}\right)$ obeying

  $$\frac{d^{2} q_{i}}{d t^{2}}=\mathrm{e}^{q_{i-1}-q_{i}}-\mathrm{e}^{q_{i}-q_{i+1}}, \quad i=1,2,3$$

  where here and throughout the subscripts are to be determined modulo 3 so that $q_{4} \equiv q_{1}$ and $q_{0} \equiv q_{3}$. Show that

  $$H\left(q_{i}, p_{i}\right)=\frac{1}{2} \sum_{i=1}^{3} p_{i}^{2}+\sum_{i=1}^{3} \mathrm{e}^{q_{i}-q_{i+1}}$$

  is a Hamiltonian for the Toda system.

  Set $a_{i}=\frac{1}{2} \exp \left(\frac{q_{i}-q_{i+1}}{2}\right)$ and $b_{i}=-\frac{1}{2} p_{i}$. Show that

  $$\frac{d a_{i}}{d t}=\left(b_{i+1}-b_{i}\right) a_{i}, \quad \frac{d b_{i}}{d t}=2\left(a_{i}^{2}-a_{i-1}^{2}\right), \quad i=1,2,3$$

  Is this coordinate transformation canonical?

  By considering the matrices

  $$L=\left(\begin{array}{lll} b_{1} & a_{1} & a_{3} \\ a_{1} & b_{2} & a_{2} \\ a_{3} & a_{2} & b_{3} \end{array}\right), \quad A=\left(\begin{array}{ccc} 0 & -a_{1} & a_{3} \\ a_{1} & 0 & -a_{2} \\ -a_{3} & a_{2} & 0 \end{array}\right)$$

  or otherwise, compute three independent first integrals of the Toda system. [Proof of independence is not required.]

  comment

• Paper 3, Section II, G

  Linear Analysis

  Part II, 2015

  State and prove the Baire Category Theorem. [Choose any version you like.]

  An isometry from a metric space $(M, d)$ to another metric space $(N, e)$ is a function $\varphi: M \rightarrow N$ such that $e(\varphi(x), \varphi(y))=d(x, y)$ for all $x, y \in M$. Prove that there exists no isometry from the Euclidean plane $\ell_{2}^{2}$ to the Banach space $c_{0}$ of sequences converging to 0 . [Hint: Assume $\varphi: \ell_{2}^{2} \rightarrow \mathrm{c}_{0}$ is an isometry. For $n \in \mathbb{N}$ and $x \in \ell_{2}^{2}$ let $\varphi_{n}(x)$ denote the $n^{\text {th }}$coordinate of $\varphi(x)$. Consider the sets $F_{n}$ consisting of all pairs $(x, y)$ with $\|x\|_{2}=\|y\|_{2}=1$ and $\|\varphi(x)-\varphi(y)\|_{\infty}=\left|\varphi_{n}(x)-\varphi_{n}(y)\right|$.]

  Show that for each $n \in \mathbb{N}$ there is a linear isometry $\ell_{1}^{n} \rightarrow \mathrm{c}_{0}$.

  comment

• Paper 4, Section II, G

  Linear Analysis

  Part II, 2015

  Let $H$ be a Hilbert space and $T \in \mathcal{B}(H)$. Define what is meant by an adjoint of $T$ and prove that it exists, it is linear and bounded, and that it is unique. [You may use the Riesz Representation Theorem without proof.]

  What does it mean to say that $T$ is a normal operator? Give an example of a bounded linear map on $\ell_{2}$ that is not normal.

  Show that $T$ is normal if and only if $\|T x\|=\left\|T^{*} x\right\|$ for all $x \in H$.

  Prove that if $T$ is normal, then $\sigma(T)=\sigma_{\mathrm{ap}}(T)$, that is, that every element of the spectrum of $T$ is an approximate eigenvalue of $T$.

  comment

• Paper 2, Section II, G

  Linear Analysis

  Part II, 2015

  (a) Let $T: X \rightarrow Y$ be a linear map between normed spaces. What does it mean to say that $T$ is bounded? Show that $T$ is bounded if and only if $T$ is continuous. Define the operator norm of $T$ and show that the set $\mathcal{B}(X, Y)$ of all bounded, linear maps from $X$ to $Y$ is a normed space in the operator norm.

  (b) For each of the following linear maps $T$, determine if $T$ is bounded. When $T$ is bounded, compute its operator norm and establish whether $T$ is compact. Justify your answers. Here $\|f\|_{\infty}=\sup _{t \in[0,1]}|f(t)|$ for $f \in C[0,1]$ and $\|f\|=\|f\|_{\infty}+\left\|f^{\prime}\right\|_{\infty}$ for $f \in C^{1}[0,1]$.

  (i) $T:\left(C^{1}[0,1],\|\cdot\|_{\infty}\right) \rightarrow\left(C^{1}[0,1],\|\cdot\|\right), T(f)=f$.

  (ii) $T:\left(C^{1}[0,1],\|\cdot\|\right) \rightarrow\left(C[0,1],\|\cdot\|_{\infty}\right), T(f)=f$.

  (iii) $T:\left(C^{1}[0,1],\|\cdot\|\right) \rightarrow\left(C[0,1],\|\cdot\|_{\infty}\right), T(f)=f^{\prime}$.

  (iv) $T:\left(C[0,1],\|\cdot\|_{\infty}\right) \rightarrow \mathbb{R}, T(f)=\int_{0}^{1} f(t) h(t) d t$, where $h$ is a given element of $C[0,1]$. [Hint: Consider first the case that $h(x) \neq 0$ for every $x \in[0,1]$, and apply $T$ to a suitable function. In the general case apply $T$ to a suitable sequence of functions.]

  comment

• Paper 1, Section II, G

  Linear Analysis

  Part II, 2015

  (a) Let $\left(e_{n}\right)_{n=1}^{\infty}$ be an orthonormal basis of an inner product space $X$. Show that for all $x \in X$ there is a unique sequence $\left(a_{n}\right)_{n=1}^{\infty}$ of scalars such that $x=\sum_{n=1}^{\infty} a_{n} e_{n}$.

  Assume now that $X$ is a Hilbert space and that $\left(f_{n}\right)_{n=1}^{\infty}$ is another orthonormal basis of $X$. Prove that there is a unique bounded linear map $U: X \rightarrow X$ such that $U\left(e_{n}\right)=f_{n}$ for all $n \in \mathbb{N}$. Prove that this map $U$ is unitary.

  (b) Let $1 \leqslant p<\infty$ with $p \neq 2$. Show that no subspace of $\ell_{2}$ is isomorphic to $\ell_{p}$. [Hint: Apply the generalized parallelogram law to suitable vectors.]

  comment

• Paper 4, Section II, I

  Logic and Set Theory

  Part II, 2015

  State the Axiom of Foundation and the Principle of $\epsilon$-Induction, and show that they are equivalent (in the presence of the other axioms of $Z F$ ). [You may assume the existence of transitive closures.]

  Explain briefly how the Principle of $\epsilon$-Induction implies that every set is a member of some $V_{\alpha}$.

  Find the ranks of the following sets:

  (i) $\{\omega+1, \omega+2, \omega+3\}$,

  (ii) the Cartesian product $\omega \times \omega$,

  (iii) the set of all functions from $\omega$ to $\omega^{2}$.

  [You may assume standard properties of rank.]

  comment

• Paper 3, Section II, I

  Logic and Set Theory

  Part II, 2015

  (i) State and prove Zorn's Lemma. [You may assume Hartogs' Lemma.] Where in your proof have you made use of the Axiom of Choice?

  (ii) Let $<$ be a partial ordering on a set $X$. Prove carefully that $<$ may be extended to a total ordering of $X$.

  What does it mean to say that $<$ is well-founded?

  If $<$ has an extension that is a well-ordering, must $<$ be well-founded? If $<$ is well-founded, must every total ordering extending it be a well-ordering? Justify your answers.

  comment

• Paper 2, Section II, I

  Logic and Set Theory

  Part II, 2015

  (a) Give the inductive and synthetic definitions of ordinal addition, and prove that they are equivalent. Give the inductive definitions of ordinal multiplication and ordinal exponentiation.

  (b) Answer, with brief justification, the following:

  (i) For ordinals $\alpha, \beta$ and $\gamma$ with $\alpha<\beta$, must we have $\alpha+\gamma<\beta+\gamma$ ? Must we have $\gamma+\alpha<\gamma+\beta$ ?

  (ii) For ordinals $\alpha$ and $\beta$ with $\alpha<\beta$, must we have $\alpha^{\omega}<\beta^{\omega}$ ?

  (iii) Is there an ordinal $\alpha>1$ such that $\alpha^{\omega}=\alpha$ ?

  (iv) Show that $\omega^{\omega_{1}}=\omega_{1}$. Is $\omega_{1}$ the least ordinal $\alpha$ such that $\omega^{\alpha}=\alpha$ ?

  [You may use standard facts about ordinal arithmetic.]

  comment

• Paper 4, Section II,

  Applications of Quantum Mechanics

  Part II, 2015

  Let $\Lambda$ be a Bravais lattice with basis vectors $\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}$. Define the reciprocal lattice $\Lambda^{*}$ and write down basis vectors $\mathbf{b}_{1}, \mathbf{b}_{2}, \mathbf{b}_{3}$ for $\Lambda^{*}$ in terms of the basis for $\Lambda$.

  A finite crystal consists of identical atoms at sites of $\Lambda$ given by

  $$\ell=n_{1} \mathbf{a}_{1}+n_{2} \mathbf{a}_{2}+n_{3} \mathbf{a}_{3} \quad \text { with } \quad 0 \leqslant n_{i}<N_{i}$$

  A particle of mass $m$ scatters off the crystal; its wavevector is $\mathbf{k}$ before scattering and $\mathbf{k}^{\prime}$ after scattering, with $|\mathbf{k}|=\left|\mathbf{k}^{\prime}\right|$. Show that the scattering amplitude in the Born approximation has the form

  $$-\frac{m}{2 \pi \hbar^{2}} \Delta(\mathbf{q}) \tilde{U}(\mathbf{q}), \quad \mathbf{q}=\mathbf{k}^{\prime}-\mathbf{k}$$

  where $U(\mathbf{x})$ is the potential due to a single atom at the origin and $\Delta(\mathbf{q})$ depends on the crystal structure. [You may assume that in the Born approximation the amplitude for scattering off a potential $V(\mathbf{x})$ is $-\left(m / 2 \pi \hbar^{2}\right) \tilde{V}(\mathbf{q})$ where tilde denotes the Fourier transform.]

  Derive an expression for $|\Delta(\mathbf{q})|$ that is valid when $e^{-i \mathbf{q} \cdot \mathbf{a}_{i}} \neq 1$. Show also that when $\mathbf{q}$ is a reciprocal lattice vector $|\Delta(\mathbf{q})|$ is equal to the total number of atoms in the crystal. Comment briefly on the significance of these results.

  Now suppose that $\Lambda$ is a face-centred-cubic lattice:

  $$\mathbf{a}_{1}=\frac{a}{2}(\hat{\mathbf{y}}+\hat{\mathbf{z}}), \quad \mathbf{a}_{2}=\frac{a}{2}(\hat{\mathbf{z}}+\hat{\mathbf{x}}), \quad \mathbf{a}_{3}=\frac{a}{2}(\hat{\mathbf{x}}+\hat{\mathbf{y}})$$

  where $a$ is a constant. Show that for a particle incident with $|\mathbf{k}|>2 \pi / a$, enhanced scattering is possible for at least two values of the scattering angle, $\theta_{1}$ and $\theta_{2}$, related by

  $$\frac{\sin \left(\theta_{1} / 2\right)}{\sin \left(\theta_{2} / 2\right)}=\frac{\sqrt{3}}{2}$$

  comment

• Paper 1, Section II, I

  Logic and Set Theory

  Part II, 2015

  State and prove the Completeness Theorem for Propositional Logic.

  [You do not need to give definitions of the various terms involved. You may assume the Deduction Theorem, provided that you state it precisely.]

  State the Compactness Theorem and the Decidability Theorem, and deduce them from the Completeness Theorem.

  Let $S$ consist of the propositions $p_{n+1} \Rightarrow p_{n}$ for $n=1,2,3, \ldots$. Does $S$ prove $p_{1}$ ? Justify your answer. [Here $p_{1}, p_{2}, p_{3}, \ldots$ are primitive propositions.]

  comment

• Paper 4, Section I, E

  Mathematical Biology

  Part II, 2015

  (i) A variant of the classic logistic population model is given by the HutchinsonWright equation

  $$\frac{d x(t)}{d t}=\alpha x(t)[1-x(t-T)]$$

  where $\alpha, T>0$. Determine the condition on $\alpha$ (in terms of $T$ ) for the constant solution $x(t)=1$ to be stable.

  (ii) Another variant of the logistic model is given by the equation

  $$\frac{d x(t)}{d t}=\alpha\left[x(t-T)-x(t)^{2}\right]$$

  where $\alpha, T>0$. Give a brief interpretation of what this model represents.

  Determine the condition on $\alpha$ (in terms of $T$ ) for the constant solution $x(t)=1$ to be stable in this model.

  comment

• Paper 3, Section I, E

  Mathematical Biology

  Part II, 2015

  The number of a certain type of annual plant in year $n$ is given by $x_{n}$. Each plant produces $k$ seeds that year and then dies before the next year. The proportion of seeds that germinate to produce a new plant the next year is given by $e^{-\gamma x_{n}}$ where $\gamma>0$. Explain briefly why the system can be described by

  $$x_{n+1}=k x_{n} e^{-\gamma x_{n}}$$

  Give conditions on $k$ for a stable positive equilibrium of the plant population size to be possible.

  Winters become milder and now a proportion $s$ of all plants survive each year $(s \in(0,1))$. Assume that plants produce seeds as before while they are alive. Show that a wider range of $k$ now gives a stable positive equilibrium population.

  comment

• Paper 2, Section I, E

  Mathematical Biology

  Part II, 2015

  An activator-inhibitor system is described by the equations

  $$\begin{aligned} \frac{\partial u}{\partial t} &=2 u+u^{2}-u v+\frac{\partial^{2} u}{\partial x^{2}} \\ \frac{\partial v}{\partial t} &=a\left(u^{2}-v\right)+d \frac{\partial^{2} v}{\partial x^{2}} \end{aligned}$$

  where $a, d>0$.

  Find the range of $a$ for which the spatially homogeneous system has a stable equilibrium solution with $u>0$ and $v>0$.

  For the case when the homogeneous system is stable, consider spatial perturbations proportional to $\cos (k x)$ to the equilibrium solution found above. Show that the system has a Turing instability when

  $$d>\left(\frac{7}{2}+2 \sqrt{3}\right) a$$

  comment

• Paper 1, Section I, E

  Mathematical Biology

  Part II, 2015

  The population density $n(a, t)$ of individuals of age $a$ at time $t$ satisfies

  $$\frac{\partial n}{\partial t}+\frac{\partial n}{\partial a}=-\mu(a) n(a, t), \quad n(0, t)=\int_{0}^{\infty} b(a) n(a, t) d a$$

  where $\mu(a)$ is the age-dependent death rate and $b(a)$ is the birth rate per individual of age $a$. Show that this may be solved with a similarity solution of the form $n(a, t)=e^{\gamma t} r(a)$ if the growth rate $\gamma$ satisfies $\phi(\gamma)=1$ where

  $$\phi(\gamma)=\int_{0}^{\infty} b(a) e^{-\gamma a-\int_{0}^{a} \mu(s) d s} d a$$

  Suppose now that the birth rate is given by $b(a)=B a^{p} e^{-\lambda a}$ with $B, \lambda>0$ and $p$ is a positive integer, and the death rate is constant in age (i.e. $\mu(a)=\mu)$. Find the average number of offspring per individual.

  Find the similarity solution, and find the threshold $B^{*}$ for the birth parameter $B$ so that $B>B^{*}$ corresponds to a growing population.

  comment

• Paper 4, Section II, E

  Mathematical Biology

  Part II, 2015

  In a stochastic model of multiple populations, $P=P(\mathbf{x}, t)$ is the probability that the population sizes are given by the vector $\mathbf{x}$ at time $t$. The jump rate $W(\mathbf{x}, \mathbf{r})$ is the probability per unit time that the population sizes jump from $\mathbf{x}$ to $\mathbf{x}+\mathbf{r}$. Under suitable assumptions, the system may be approximated by the multivariate Fokker-Planck equation (with summation convention)

  $$\frac{\partial}{\partial t} P=-\frac{\partial}{\partial x_{i}} A_{i} P+\frac{1}{2} \frac{\partial^{2}}{\partial x_{i} \partial x_{j}} B_{i j} P$$

  where $A_{i}(\mathbf{x})=\sum_{\mathbf{r}} r_{i} W(\mathbf{x}, \mathbf{r})$ and matrix elements $B_{i j}(\mathbf{x})=\sum_{\mathbf{r}} r_{i} r_{j} W(\mathbf{x}, \mathbf{r})$.

  (a) Use the multivariate Fokker-Planck equation to show that

  $$\begin{aligned} \frac{d}{d t}\left\langle x_{k}\right\rangle &=\left\langle A_{k}\right\rangle \\ \frac{d}{d t}\left\langle x_{k} x_{l}\right\rangle &=\left\langle x_{l} A_{k}+x_{k} A_{l}+B_{k l}\right\rangle \end{aligned}$$

  [You may assume that $P(\mathbf{x}, t) \rightarrow 0$ as $|\mathbf{x}| \rightarrow \infty$.]

  (b) For small fluctuations, you may assume that the vector $\mathbf{A}$ may be approximated by a linear function in $\mathbf{x}$ and the matrix $\mathbf{B}$ may be treated as constant, i.e. $A_{k}(\mathbf{x}) \approx$ $a_{k l}\left(x_{l}-\left\langle x_{l}\right\rangle\right)$ and $B_{k l}(\mathbf{x}) \approx B_{k l}(\langle\mathbf{x}\rangle)=b_{k l}$ (where $a_{k l}$ and $b_{k l}$ are constants). Show that at steady state the covariances $C_{i j}=\operatorname{cov}\left(x_{i}, x_{j}\right)$ satisfy

  $$a_{i k} C_{j k}+a_{j k} C_{i k}+b_{i j}=0 .$$

  (c) A lab-controlled insect population consists of $x_{1}$ larvae and $x_{2}$ adults. Larvae are added to the system at rate $\lambda$. Larvae each mature at rate $\gamma$ per capita. Adults die at rate $\beta$ per capita. Give the vector $\mathbf{A}$ and matrix $\mathbf{B}$ for this model. Show that at steady state

  $$\left\langle x_{1}\right\rangle=\frac{\lambda}{\gamma}, \quad\left\langle x_{2}\right\rangle=\frac{\lambda}{\beta} .$$

  (d) Find the variance of each population size near steady state, and show that the covariance between the populations is zero.

  comment

• Paper 3, Section II, E

  Mathematical Biology

  Part II, 2015

  A fungal disease is introduced into an isolated population of frogs. Without disease, the normalised population size $x$ would obey the logistic equation $\dot{x}=x(1-x)$, where the dot denotes differentiation with respect to time. The disease causes death at rate $d$ and there is no recovery. The disease transmission rate is $\beta$ and, in addition, offspring of infected frogs are infected from birth.

  (a) Briefly explain why the population sizes $x$ and $y$ of uninfected and infected frogs respectively now satisfy

  $$\begin{aligned} \dot{x} &=x[1-x-(1+\beta) y] \\ \dot{y} &=y[(1-d)-(1-\beta) x-y] \end{aligned}$$

  (b) The population starts at the disease-free population size $(x=1)$ and a small number of infected frogs are introduced. Show that the disease will successfully invade if and only if $\beta>d$.

  (c) By finding all the equilibria in $x \geqslant 0, y \geqslant 0$ and considering their stability, find the long-term outcome for the frog population. State the relationships between $d$ and $\beta$ that distinguish different final populations.

  (d) Plot the long-term steady total population size as a function of $d$ for fixed $\beta$, and note that an intermediate mortality rate is actually the most harmful. Explain why this is the case.

  comment

• Paper 4, Section II, H

  Number Fields

  Part II, 2015

  Let $K$ be a number field. State Dirichlet's unit theorem, defining all the terms you use, and what it implies for a quadratic field $\mathbb{Q}(\sqrt{d})$, where $d \neq 0,1$ is a square-free integer.

  Find a fundamental unit of $\mathbb{Q}(\sqrt{26})$.

  Find all integral solutions $(x, y)$ of the equation $x^{2}-26 y^{2}=\pm 10$.

  comment

• Paper 2, Section II, H

  Number Fields

  Part II, 2015

  (i) Let $d \equiv 2$ or $3 \bmod 4$. Show that $(p)$ remains prime in $\mathcal{O}_{\mathbb{Q}(\sqrt{d})}$ if and only if $x^{2}-d$ is irreducible $\bmod p$.

  (ii) Factorise $(2)$, (3) in $\mathcal{O}_{K}$, when $K=\mathbb{Q}(\sqrt{-14})$. Compute the class group of $K$.

  comment

• Paper 1, Section II, $16 \mathrm{H}$

  Number Fields

  Part II, 2015

  (a) Let $K$ be a number field, and $f$ a monic polynomial whose coefficients are in $\mathcal{O}_{K}$. Let $M$ be a field containing $K$ and $\alpha \in M$. Show that if $f(\alpha)=0$, then $\alpha$ is an algebraic integer.

  Hence conclude that if $h \in K[x]$ is monic, with $h^{n} \in \mathcal{O}_{K}[x]$, then $h \in \mathcal{O}_{K}[x]$.

  (b) Compute an integral basis for $\mathcal{O}_{\mathbb{Q}(\alpha)}$ when the minimum polynomial of $\alpha$ is $x^{3}-x-4$.

  comment

• Paper 2, Section II, A

  Applications of Quantum Mechanics

  Part II, 2015

  A beam of particles of mass $m$ and energy $\hbar^{2} k^{2} / 2 m$ is incident on a target at the origin described by a spherically symmetric potential $V(r)$. Assuming the potential decays rapidly as $r \rightarrow \infty$, write down the asymptotic form of the wavefunction, defining the scattering amplitude $f(\theta)$.

  Consider a free particle with energy $\hbar^{2} k^{2} / 2 m$. State, without proof, the general axisymmetric solution of the Schrödinger equation for $r>0$ in terms of spherical Bessel and Neumann functions $j_{\ell}$ and $n_{\ell}$, and Legendre polynomials $P_{\ell}(\ell=0,1,2, \ldots)$. Hence define the partial wave phase shifts $\delta_{\ell}$ for scattering from a potential $V(r)$ and derive the partial wave expansion for $f(\theta)$ in terms of phase shifts.

  Now suppose

  $$V(r)=\left\{\begin{array}{cc} \hbar^{2} \gamma^{2} / 2 m & r<a \\ 0 & r>a \end{array}\right.$$

  with $\gamma>k$. Show that the S-wave phase shift $\delta_{0}$ obeys

  $$\frac{\tanh (\kappa a)}{\kappa a}=\frac{\tan \left(k a+\delta_{0}\right)}{k a}$$

  where $\kappa^{2}=\gamma^{2}-k^{2}$. Deduce that for an S-wave solution

  $$f \rightarrow \frac{\tanh \gamma a-\gamma a}{\gamma} \quad \text { as } \quad k \rightarrow 0$$

  [You may assume : $\quad \exp (i k r \cos \theta)=\sum_{\ell=0}^{\infty}(2 \ell+1) i^{\ell} j_{\ell}(k r) P_{\ell}(\cos \theta)$

  and $j_{\ell}(\rho) \sim \frac{1}{\rho} \sin (\rho-\ell \pi / 2), \quad n_{\ell}(\rho) \sim-\frac{1}{\rho} \cos (\rho-\ell \pi / 2) \quad$ as $\left.\quad \rho \rightarrow \infty .\right]$

  comment

• Paper 4, Section I, H

  Number Theory

  Part II, 2015

  Show that if $10^{n}+1$ is prime then $n$ must be a power of 2 . Now assuming $n$ is a power of 2 , show that if $p$ is a prime factor of $10^{n}+1$ then $p \equiv 1(\bmod 2 n)$.

  Explain the method of Fermat factorization, and use it to factor $10^{4}+1$.

  comment

• Paper 3, Section I, H

  Number Theory

  Part II, 2015

  What does it mean to say that a positive definite binary quadratic form is reduced? Find the three smallest positive integers properly represented by each of the forms $f(x, y)=3 x^{2}+8 x y+9 y^{2}$ and $g(x, y)=15 x^{2}+34 x y+20 y^{2}$. Show that every odd integer represented by some positive definite binary quadratic form with discriminant $-44$ is represented by at least one of the forms $f$ and $g$.

  comment

• Paper 2, Section I, H

  Number Theory

  Part II, 2015

  Define the Euler totient function $\phi$ and the Möbius function $\mu$. Suppose $f$ and $g$ are functions defined on the natural numbers satisfying $f(n)=\sum_{d \mid n} g(d)$. State and prove a formula for $g$ in terms of $f$. Find a relationship between $\mu$ and $\phi$.

  Define the Riemann zeta function $\zeta(s)$. Find a Dirichlet series for $\zeta(s-1) / \zeta(s)$ valid for $\operatorname{Re}(s)>2$.

  comment

• Paper 1, Section I, H

  Number Theory

  Part II, 2015

  Define the Legendre symbol $\left(\frac{a}{p}\right)$. State and prove Euler's criterion, assuming if you wish the existence of primitive roots $\bmod p$.

  By considering the prime factors of $n^{2}+4$ for $n$ an odd integer, prove that there are infinitely many primes $p$ with $p \equiv 5(\bmod 8)$.

  comment

• Paper 4, Section II, H

  Number Theory

  Part II, 2015

  State the Chinese Remainder Theorem.

  Let $N$ be an odd positive integer. Define the Jacobi symbol $\left(\frac{a}{N}\right)$. Which of the following statements are true, and which are false? Give a proof or counterexample as appropriate.

  (i) If $\left(\frac{a}{N}\right)=1$ then the congruence $x^{2} \equiv a(\bmod N)$ is soluble.

  (ii) If $N$ is not a square then $\sum_{a=1}^{N}\left(\frac{a}{N}\right)=0$.

  (iii) If $N$ is composite then there exists an integer a coprime to $N$ with

  $$a^{N-1} \not \equiv 1 \quad(\bmod N)$$

  (iv) If $N$ is composite then there exists an integer $a$ coprime to $N$ with

  $$a^{(N-1) / 2} \not \equiv\left(\frac{a}{N}\right) \quad(\bmod N)$$

  comment

• Paper 3, Section II, H

  Number Theory

  Part II, 2015

  Let $\theta$ be a real number with continued fraction expansion $\left[a_{0}, a_{1}, a_{2}, \ldots\right]$. Define the convergents $p_{n} / q_{n}$ (by means of recurrence relations) and show that for $\beta>0$ we have

  $$\left[a_{0}, a_{1}, \ldots, a_{n-1}, \beta\right]=\frac{\beta p_{n-1}+p_{n-2}}{\beta q_{n-1}+q_{n-2}}$$

  Show that

  $$\left|\theta-\frac{p_{n}}{q_{n}}\right|<\frac{1}{q_{n} q_{n+1}}$$

  and deduce that $p_{n} / q_{n} \rightarrow \theta$ as $n \rightarrow \infty$.

  By computing a suitable continued fraction expansion, find solutions in positive integers $x$ and $y$ to each of the equations $x^{2}-53 y^{2}=4$ and $x^{2}-53 y^{2}=-7$.

  comment

• Paper 4, Section II, E

  Numerical Analysis

  Part II, 2015

  (a) Define the $m$ th Krylov space $K_{m}(A, v)$ for $A \in \mathbb{R}^{n \times n}$ and $0 \neq v \in \mathbb{R}^{n}$. Letting $\delta_{m}$ be the dimension of $K_{m}(A, v)$, prove the following results.

  (i) There exists a positive integer $s \leqslant n$ such that $\delta_{m}=m$ for $m \leqslant s$ and $\delta_{m}=s$ for $m>s$.

  (ii) If $v=\sum_{i=1}^{s^{\prime}} c_{i} w_{i}$, where $w_{i}$ are eigenvectors of $A$ for distinct eigenvalues and all $c_{i}$ are nonzero, then $s=s^{\prime}$.

  (b) Define the term residual in the conjugate gradient (CG) method for solving a system $A x=b$ with symmetric positive definite $A$. Explain (without proof) the connection to Krylov spaces and prove that for any right-hand side $b$ the CG method finds an exact solution after at most $t$ steps, where $t$ is the number of distinct eigenvalues of $A$. [You may use without proof known properties of the iterates of the CG method.]

  Define what is meant by preconditioning, and explain two ways in which preconditioning can speed up convergence. Can we choose the preconditioner so that the CG method requires only one step? If yes, is it a reasonable method for speeding up the computation?

  comment

• Paper 2, Section II, E

  Numerical Analysis

  Part II, 2015

  (a) The boundary value problem $-\Delta u+c u=f$ on the unit square $[0,1]^{2}$ with zero boundary conditions and scalar constant $c>0$ is discretised using finite differences as

  $$\begin{array}{r} -u_{i-1, j}-u_{i+1, j}-u_{i, j-1}-u_{i, j+1}+4 u_{i, j}+c h^{2} u_{i, j}=h^{2} f(i h, j h), \\ i, j=1, \ldots, m \end{array}$$

  with $h=1 /(m+1)$. Show that for the resulting system $A u=b$, for a suitable matrix $A$ and vectors $u$ and $b$, both the Jacobi and Gauss-Seidel methods converge. [You may cite and use known results on the discretised Laplace operator and on the convergence of iterative methods.]

  Define the Jacobi method with relaxation parameter $\omega$. Find the eigenvalues $\lambda_{k, l}$ of the iteration matrix $H_{\omega}$ for the above problem and show that, in order to ensure convergence for all $h$, the condition $0<\omega \leqslant 1$ is necessary.

  [Hint: The eigenvalues of the discretised Laplace operator in two dimensions are $4\left(\sin ^{2} \frac{\pi k h}{2}+\sin ^{2} \frac{\pi l h}{2}\right)$ for integers $k, l$.]

  (b) Explain the components and steps in a multigrid method for solving the Poisson equation, discretised as $A_{h} u_{h}=b_{h}$. If we use the relaxed Jacobi method within the multigrid method, is it necessary to choose $\omega \neq 1$ to get fast convergence? Explain why or why not.

  comment

• Paper 3, Section II, E

  Numerical Analysis

  Part II, 2015

  (a) Given the finite-difference recurrence

  $$\sum_{k=r}^{s} a_{k} u_{m+k}^{n+1}=\sum_{k=r}^{s} b_{k} u_{m+k}^{n}, \quad m \in \mathbb{Z}, n \in \mathbb{Z}^{+}$$

  that discretises a Cauchy problem, the amplification factor is defined by

  $$H(\theta)=\left(\sum_{k=r}^{s} b_{k} e^{i k \theta}\right) /\left(\sum_{k=r}^{s} a_{k} e^{i k \theta}\right)$$

  Show how $H(\theta)$ acts on the Fourier transform $\hat{u}^{n}$ of $u^{n}$. Hence prove that the method is stable if and only if $|H(\theta)| \leqslant 1$ for all $\theta \in[-\pi, \pi]$.

  (b) The two-dimensional diffusion equation

  $$u_{t}=u_{x x}+c u_{y y}$$

  for some scalar constant $c>0$ is discretised with the forward Euler scheme

  $$u_{i, j}^{n+1}=u_{i, j}^{n}+\mu\left(u_{i+1, j}^{n}-2 u_{i, j}^{n}+u_{i-1, j}^{n}+c u_{i, j+1}^{n}-2 c u_{i, j}^{n}+c u_{i, j-1}^{n}\right)$$

  Using Fourier stability analysis, find the range of values $\mu>0$ for which the scheme is stable.

  comment

• Paper 1, Section II, 38E

  Numerical Analysis

  Part II, 2015

  (a) The diffusion equation

  $$\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}\left(a(x) \frac{\partial u}{\partial x}\right) \quad \text { in } \quad 0 \leqslant x \leqslant 1, \quad t \geqslant 0$$

  with the initial condition $u(x, 0)=\phi(x)$ in $0 \leqslant x \leqslant 1$ and zero boundary conditions at $x=0$ and $x=1$, is solved by the finite-difference method

  $$\begin{array}{r} u_{m}^{n+1}=u_{m}^{n}+\mu\left[a_{m-\frac{1}{2}} u_{m-1}^{n}-\left(a_{m-\frac{1}{2}}+a_{m+\frac{1}{2}}\right) u_{m}^{n}+a_{m+\frac{1}{2}} u_{m+1}^{n}\right] \\ m=1,2, \ldots, M \end{array}$$

  where $\mu=k / h^{2}, k=\Delta t, h=1 /(M+1), u_{m}^{n} \approx u(m h, n k)$, and $a_{\alpha}=a(\alpha h)$.

  Assuming that the function $a$ and the exact solution are sufficiently smooth, prove that the exact solution satisfies the numerical scheme with error $O\left(h^{3}\right)$ for constant $\mu$.

  (b) For the problem in part (a), assume that there exist $0<a_{-}<a_{+}<\infty$ such that $a_{-} \leqslant a(x) \leqslant a_{+}$for all $0 \leqslant x \leqslant 1$. State (without proof) the Gershgorin theorem and prove that the method is stable for $0<\mu \leqslant 1 /\left(2 a_{+}\right)$.

  comment