Paper 3, Section II, C
(a) A sample of gas has pressure , volume , temperature and entropy .
(i) Use the first law of thermodynamics to derive the Maxwell relation
(ii) Define the heat capacity at constant pressure and the enthalpy and show that .
(b) Consider a perfectly insulated pipe with a throttle valve, as shown.
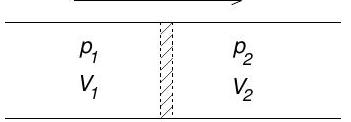
Gas initially occupying volume on the left is forced slowly through the valve at constant pressure . A constant pressure is maintained on the right and the final volume occupied by the gas after passing through the valve is .
(i) Show that the enthalpy of the gas is unchanged by this process.
(ii) The Joule-Thomson coefficient is defined to be . Show that
[You may assume the identity ]
(iii) Suppose that the gas obeys an equation of state
where is the number of particles. Calculate to first order in and hence derive a condition on for obtaining a positive Joule-Thomson coefficient.