Paper 4, Section I, B
Part II, 2015
Explain how the Papperitz symbol
represents a differential equation with certain properties. [You need not write down the differential equation explicitly.]
The hypergeometric function is defined to be the solution of the equation given by the Papperitz symbol
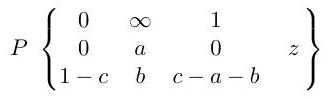
that is analytic at and such that . Show that
indicating clearly any general results for manipulating Papperitz symbols that you use.