Part II 2016

• Paper 3, Section II, H

  Algebraic Geometry

  Part II, 2016

  (a) Let $X$ be an affine variety. Define the tangent space of $X$ at a point $P$. Say what it means for the variety to be singular at $P$.

  Define the dimension of $X$ in terms of (i) the tangent spaces of $X$, and (ii) Krull dimension.

  (b) Consider the ideal $I$ generated by the set $\left\{y, y^{2}-x^{3}+x y^{3}\right\} \subseteq k[x, y]$. What is $Z(I) \subseteq \mathbb{A}^{2} ?$

  Using the generators of the ideal, calculate the tangent space of a point in $Z(I)$. What has gone wrong? [A complete argument is not necessary.]

  (c) Calculate the dimension of the tangent space at each point $p \in X$ for $X=$ $Z\left(x-y^{2}, x-z w\right) \subseteq \mathbb{A}^{4}$, and determine the location of the singularities of $X .$

  comment

• Paper 2, Section II, H

  Algebraic Geometry

  Part II, 2016

  In this question we work over an algebraically closed field of characteristic zero. Let $X^{o}=Z\left(x^{6}+x y^{5}+y^{6}-1\right) \subset \mathbb{A}^{2}$ and let $X \subset \mathbb{P}^{2}$ be the closure of $X^{o}$ in $\mathbb{P}^{2} .$

  (a) Show that $X$ is a non-singular curve.

  (b) Show that $\omega=d x /\left(5 x y^{4}+6 y^{5}\right)$ is a regular differential on $X$.

  (c) Compute the divisor of $\omega$. What is the genus of $X$ ?

  comment

• Paper 4, Section II, A

  Applications of Quantum Mechanics

  Part II, 2016

  Let $\Lambda \subset \mathbb{R}^{2}$ be a Bravais lattice. Define the dual lattice $\Lambda^{*}$ and show that

  $$V(\mathbf{x})=\sum_{\mathbf{q} \in \Lambda^{*}} V_{\mathbf{q}} \exp (i \mathbf{q} \cdot \mathbf{x})$$

  obeys $V(\mathbf{x}+l)=V(\mathbf{x})$ for all $l \in \Lambda$, where $V_{\mathbf{q}}$ are constants. Suppose $V(\mathbf{x})$ is the potential for a particle of mass $m$ moving in a two-dimensional crystal that contains a very large number of lattice sites of $\Lambda$ and occupies an area $\mathcal{A}$. Adopting periodic boundary conditions, plane-wave states $|\mathbf{k}\rangle$ can be chosen such that

  $$\langle\mathbf{x} \mid \mathbf{k}\rangle=\frac{1}{\mathcal{A}^{1 / 2}} \exp (i \mathbf{k} \cdot \mathbf{x}) \quad \text { and } \quad\left\langle\mathbf{k} \mid \mathbf{k}^{\prime}\right\rangle=\delta_{\mathbf{k} \mathbf{k}^{\prime}}$$

  The allowed wavevectors $\mathbf{k}$ are closely spaced and include all vectors in $\Lambda^{*}$. Find an expression for the matrix element $\left\langle\mathbf{k}|V(\mathbf{x})| \mathbf{k}^{\prime}\right\rangle$ in terms of the coefficients $V_{\mathbf{q}}$. [You need not discuss additional details of the boundary conditions.]

  Now suppose that $V(\mathbf{x})=\lambda U(\mathbf{x})$, where $\lambda \ll 1$ is a dimensionless constant. Find the energy $E(\mathbf{k})$ for a particle with wavevector $\mathbf{k}$ to order $\lambda^{2}$ in non-degenerate perturbation theory. Show that this expansion in $\lambda$ breaks down on the Bragg lines in k-space defined by the condition

  $$\mathbf{k} \cdot \mathbf{q}=\frac{1}{2}|\mathbf{q}|^{2} \quad \text { for } \quad \mathbf{q} \in \Lambda^{*}$$

  and explain briefly, without additional calculations, the significance of this for energy levels in the crystal.

  Consider the particular case in which $\Lambda$ has primitive vectors

  $$\mathbf{a}_{1}=2 \pi\left(\mathbf{i}+\frac{1}{\sqrt{3}} \mathbf{j}\right), \quad \mathbf{a}_{2}=2 \pi \frac{2}{\sqrt{3}} \mathbf{j}$$

  where $\mathbf{i}$ and $\mathbf{j}$ are orthogonal unit vectors. Determine the polygonal region in $\mathbf{k}$-space corresponding to the lowest allowed energy band.

  comment

• Paper 4, Section II, 10I

  Number Theory

  Part II, 2016

  (a) Define Euler's totient function $\phi(n)$ and show that $\sum_{d \mid n} \phi(d)=n$.

  (b) State Lagrange's theorem concerning roots of polynomials mod $p$.

  (c) Let $p$ be a prime. Proving any results you need about primitive roots, show that $x^{m} \equiv 1(\bmod p)$ has exactly $(m, p-1)$ roots.

  (d) Show that if $p$ and $3 p-2$ are both primes then $N=p(3 p-2)$ is a Fermat pseudoprime for precisely a third of all bases.

  comment

• Paper 3, Section II, I

  Number Theory

  Part II, 2016

  What does it mean for a positive definite binary quadratic form to be reduced?

  Prove that every positive definite binary quadratic form is equivalent to a reduced form, and that there are only finitely many reduced forms with given discriminant.

  State a criterion for a positive integer $n$ to be represented by a positive definite binary quadratic form with discriminant $d<0$, and hence determine which primes $p$ are represented by $x^{2}+x y+7 y^{2}$.

  comment

• Paper 4, Section II, B

  Numerical Analysis

  Part II, 2016

  (a) Describe an implementation of the power method for determining the eigenvalue of largest modulus and its associated eigenvector for a matrix that has a unique eigenvalue of largest modulus.

  Now let $A$ be a real $n \times n$ matrix with distinct eigenvalues satisfying $\left|\lambda_{n}\right|=\left|\lambda_{n-1}\right|$ and $\left|\lambda_{n}\right|>\left|\lambda_{i}\right|, i=1, \ldots, n-2$. The power method is applied to $A$, with an initial condition $\mathbf{x}^{(0)}=\sum_{i=1}^{n} c_{i} \mathbf{w}_{i}$ such that $c_{n-1} c_{n} \neq 0$, where $\mathbf{w}_{i}$ is the eigenvector associated with $\lambda_{i}$. Show that the power method does not converge. Explain why $\mathbf{x}^{(k)}, \mathbf{x}^{(k+1)}$ and $\mathbf{x}^{(k+2)}$ become linearly dependent as $k \rightarrow \infty$.

  (b) Consider the following variant of the power method, called the two-stage power method, applied to the matrix $A$ of part (a):

  1. Pick $\mathbf{x}^{(0)} \in \mathbb{R}^{n}$ satisfying $\left\|\mathbf{x}^{(0)}\right\|=1$. Let $0<\varepsilon \ll 1$. Set $k=0$ and $\mathbf{x}^{(1)}=A \mathbf{x}^{(0)}$.

  2. Calculate $\mathbf{x}^{(k+2)}=A \mathbf{x}^{(k+1)}$ and calculate $\alpha, \beta$ that minimise

  $$f(\alpha, \beta)=\left\|\mathbf{x}^{(k+2)}+\alpha \mathbf{x}^{(k+1)}+\beta \mathbf{x}^{(k)}\right\| .$$

  2. If $f(\alpha, \beta) \leqslant \varepsilon$, solve $\lambda^{2}+\alpha \lambda+\beta=0$ and let the roots be $\lambda_{1}$ and $\lambda_{2}$. They are accepted as eigenvalues of $A$, and the corresponding eigenvectors are estimated as $\mathbf{x}^{(k+1)}-\lambda_{2} \mathbf{x}^{(k)}$ and $\mathbf{x}^{(k+1)}-\lambda_{1} \mathbf{x}^{(k)}$.

  3. Otherwise, divide $\mathbf{x}^{(k+2)}$ and $\mathbf{x}^{(k+1)}$ by the current value of $\left\|\mathbf{x}^{(k+1)}\right\|$, increase $k$ by 1 and return to Step $\mathbf{1}$.

  Explain the justification behind Step 2 of the algorithm.

  (c) Let $n=3$, and suppose that, for a large value of $k$, the two-stage power method yields the vectors

  $$\mathbf{y}_{k}=\mathbf{x}^{(k)}=\left(\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right), \quad \mathbf{y}_{k+1}=A \mathbf{x}^{(k)}=\left(\begin{array}{c} 2 \\ 3 \\ 4 \end{array}\right), \quad \mathbf{y}_{k+2}=A^{2} \mathbf{x}^{(k)}=\left(\begin{array}{c} 2 \\ 4 \\ 6 \end{array}\right)$$

  Find two eigenvalues of $A$ and the corresponding eigenvectors.

  comment

• Paper 2, Section II, B

  Numerical Analysis

  Part II, 2016

  (a) The advection equation

  $$u_{t}=u_{x}, \quad 0 \leqslant x \leqslant 1, t \geqslant 0$$

  is discretised using an equidistant grid with stepsizes $\Delta x=h$ and $\Delta t=k$. The spatial derivatives are approximated with central differences and the resulting ODEs are approximated with the trapezoidal rule. Write down the relevant difference equation for determining $\left(u_{m}^{n+1}\right)$ from $\left(u_{m}^{n}\right)$. What is the name of this scheme? What is the local truncation error?

  The boundary condition is periodic, $u(0, t)=u(1, t)$. Explain briefly how to write the discretised scheme in the form $B \mathbf{u}^{n+1}=C \mathbf{u}^{n}$, where the matrices $B$ and $C$, to be identified, have a circulant form. Using matrix analysis, find the range of $\mu=\Delta t / \Delta x$ for which the scheme is stable. [Standard results may be used without proof if quoted carefully.]

  [Hint: An $n \times n$ circulant matrix has the form

  $$A=\left(\begin{array}{cccc} a_{0} & a_{1} & \cdots & a_{n-1} \\ a_{n-1} & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & a_{1} \\ a_{1} & \cdots & a_{n-1} & a_{0} \end{array}\right)$$

  All such matrices have the same set of eigenvectors $\mathbf{v}_{\ell}=\left(\omega^{j \ell}\right)_{j=0}^{n-1}, \ell=0,1, \ldots, n-1$, where $\omega=e^{2 \pi i / n}$, and the corresponding eigenvalues are $\lambda_{\ell}=\sum_{k=0}^{n-1} a_{k} \omega^{k \ell}$.]

  (b) Consider the advection equation on the unit square

  $$u_{t}=a u_{x}+b u_{y}, \quad 0 \leqslant x, y \leqslant 1, t \geqslant 0$$

  where $u$ satisfies doubly periodic boundary conditions, $u(0, y)=u(1, y), u(x, 0)=u(x, 1)$, and $a(x, y)$ and $b(x, y)$ are given doubly periodic functions. The system is discretised with the Crank-Nicolson scheme, with central differences for the space derivatives, using an equidistant grid with stepsizes $\Delta x=\Delta y=h$ and $\Delta t=k$. Write down the relevant difference equation, and show how to write the scheme in the form

  $$\mathbf{u}^{n+1}=\left(I-\frac{1}{4} \mu A\right)^{-1}\left(I+\frac{1}{4} \mu A\right) \mathbf{u}^{n}$$

  where the matrix $A$ should be identified. Describe how (*) can be approximated by Strang splitting, and explain the advantages of doing so.

  [Hint: Inversion of the matrix $B$ in part (a) has a similar computational cost to that of a tridiagonal matrix.]

  comment

• Paper 1, Section II, B

  Numerical Analysis

  Part II, 2016

  (a) Consider the periodic function

  $$f(x)=5+2 \cos \left(2 \pi x-\frac{\pi}{2}\right)+3 \cos (4 \pi x)$$

  on the interval $[0,1]$. The $N$-point discrete Fourier transform of $f$ is defined by

  $$F_{N}(n)=\frac{1}{N} \sum_{k=0}^{N-1} f_{k} \omega_{N}^{-n k}, \quad n=0,1, \ldots, N-1$$

  where $\omega_{N}=e^{2 \pi i / N}$ and $f_{k}=f(k / N)$. Compute $F_{4}(n), n=0, \ldots, 3$, using the Fast Fourier Transform (FFT). Compare your result with what you get by computing $F_{4}(n)$ directly from $(*)$. Carefully explain all your computations.

  (b) Now let $f$ be any analytic function on $\mathbb{R}$ that is periodic with period 1 . The continuous Fourier transform of $f$ is defined by

  $$\hat{f}_{n}=\int_{0}^{1} f(\tau) e^{-2 \pi i n \tau} d \tau, \quad n \in \mathbb{Z}$$

  Use integration by parts to show that the Fourier coefficients $\hat{f}_{n}$ decay spectrally.

  Explain what it means for the discrete Fourier transform of $f$ to approximate the continuous Fourier transform with spectral accuracy. Prove that it does so.

  What can you say about the behaviour of $F_{N}(N-n)$ as $N \rightarrow \infty$ for fixed $n$ ?

  comment

• Paper 3, Section II, B

  Numerical Analysis

  Part II, 2016

  (a) Define the Jacobi and Gauss-Seidel iteration schemes for solving a linear system of the form $A \mathbf{u}=\mathbf{b}$, where $\mathbf{u}, \mathbf{b} \in \mathbb{R}^{M}$ and $A \in \mathbb{R}^{M \times M}$, giving formulae for the corresponding iteration matrices $H_{J}$ and $H_{G S}$ in terms of the usual decomposition $A=L_{0}+D+U_{0}$.

  Show that both iteration schemes converge when $A$ results from discretization of Poisson's equation on a square with the five-point formula, that is when

  $$A=\left[\begin{array}{rrrrr} S & I & & & \\ I & S & I & & \\ & \ddots & \ddots & \ddots & \\ & & I & S & I \\ & & & I & S \end{array}\right], \quad S=\left[\begin{array}{rrrrr} -4 & 1 & & & \\ 1 & -4 & 1 & & \\ & \ddots & \ddots & \ddots & \\ & & 1 & -4 & 1 \\ & & & 1 & -4 \end{array}\right] \in \mathbb{R}^{m \times m}$$

  and $M=m^{2}$. [You may state the Householder-John theorem without proof.]

  (b) For the matrix $A$ given in $(*)$ :

  (i) Calculate the eigenvalues of $H_{J}$ and deduce its spectral radius $\rho\left(H_{J}\right)$.

  (ii) Show that each eigenvector $\mathbf{q}$ of $H_{G S}$ is related to an eigenvector $\mathbf{p}$ of $H_{J}$ by a transformation of the form $q_{i, j}=\alpha^{i+j} p_{i, j}$ for a suitable value of $\alpha$.

  (iii) Deduce that $\rho\left(H_{G S}\right)=\rho^{2}\left(H_{J}\right)$. What is the significance of this result for the two iteration schemes?

  [Hint: You may assume that the eigenvalues of the matrix $A$ in $(*)$ are

  $$\lambda_{k, \ell}=-4\left(\sin ^{2} \frac{x}{2}+\sin ^{2} \frac{y}{2}\right), \quad \text { where } x=\frac{k \pi h}{m+1}, y=\frac{\ell \pi h}{m+1}, \quad k, \ell=1, \ldots, m,$$

  with corresponding eigenvectors $\left.\mathbf{v}=\left(v_{i, j}\right), \quad v_{i, j}=\sin i x \sin j y, \quad i, j=1, \ldots, m . \quad\right]$

  comment

• Paper 3, Section II, K

  Optimization and Control

  Part II, 2016

  Consider the system in scalar variables, for $t=1,2, \ldots, h$ :

  $$\begin{aligned} x_{t} &=x_{t-1}+u_{t-1} \\ y_{t} &=x_{t-1}+\eta_{t} \\ \hat{x}_{0} &=x_{0}+\eta_{0} \end{aligned}$$

  where $\hat{x}_{0}$ is given, $y_{t}, u_{t}$ are observed at $t$, but $x_{0}, x_{1}, \ldots$ and $\eta_{0}, \eta_{1}, \ldots$ are unobservable, and $\eta_{0}, \eta_{1}, \ldots$ are independent random variables with mean 0 and variance $v$. Define $\hat{x}_{t-1}$ to be the estimator of $x_{t-1}$ with minimum variance amongst all estimators that are unbiased and linear functions of $W_{t-1}=\left(\hat{x}_{0}, y_{1}, \ldots, y_{t-1}, u_{0}, \ldots, u_{t-2}\right)$. Suppose $\hat{x}_{t-1}=a^{T} W_{t-1}$ and its variance is $V_{t-1}$. After observation at $t$ of $\left(y_{t}, u_{t-1}\right)$, a new unbiased estimator of $x_{t-1}$, linear in $W_{t}$, is expressed

  $$x_{t-1}^{*}=(1-H) b^{T} W_{t-1}+H y_{t}$$

  Find $b$ and $H$ to minimize the variance of $x_{t-1}^{*}$. Hence find $\hat{x}_{t}$ in terms of $\hat{x}_{t-1}, y_{t}, u_{t-1}$, $V_{t-1}$ and $v$. Calculate $V_{h}$.

  Suppose $\eta_{0}, \eta_{1}, \ldots$ are Gaussian and thus $\hat{x}_{t}=E\left[x_{t} \mid W_{t}\right]$. Consider minimizing $E\left[x_{h}^{2}+\sum_{t=0}^{h-1} u_{t}^{2}\right]$, under the constraint that the control $u_{t}$ can only depend on $W_{t}$. Show that the value function of dynamic programming for this problem can be expressed

  $$F\left(W_{t}\right)=\Pi_{t} \hat{x}_{t}^{2}+\cdots$$

  where $F\left(W_{h}\right)=\hat{x}_{h}^{2}+V_{h}$ and $+\cdots$ is independent of $W_{t}$ and linear in $v$.

  comment

• Paper 4, Section II, K

  Optimization and Control

  Part II, 2016

  State transversality conditions that can be used with Pontryagin's maximum principle and say when they are helpful.

  Given $T$, it is desired to maximize $c_{1} x_{1}(T)+c_{2} x_{2}(T)$, where

  $$\begin{aligned} &\dot{x}_{1}=u_{1}\left(a_{1} x_{1}+a_{2} x_{2}\right), \\ &\dot{x}_{2}=u_{2}\left(a_{1} x_{1}+a_{2} x_{2}\right), \end{aligned}$$

  and $u=\left(u_{1}, u_{2}\right)$ is a time-varying control such that $u_{1} \geqslant 0, u_{2} \geqslant 0$ and $u_{1}+u_{2}=1$. Suppose that $x_{1}(0)$ and $x_{2}(0)$ are positive, and that $0<a_{2}<a_{1}$ and $0<c_{1}<c_{2}$. Find the optimal control at times close to $T$. Show that over $[0, T]$ the optimal control is constant, or makes exactly one switch, the latter happening if and only if

  $$c_{2} e^{a_{2} T}<c_{1}+\frac{a_{1} c_{2}}{a_{2}}\left(e^{a_{2} T}-1\right)$$

  comment

• Paper 2, Section II, K

  Optimization and Control

  Part II, 2016

  Consider a Markov decision problem with finite state space $X$, value function $F$ and dynamic programming equation $F=\mathcal{L} F$, where

  $$(\mathcal{L} \phi)(i)=\min _{a \in\{0,1\}}\left\{c(i, a)+\beta \sum_{j \in X} P_{i j}(a) \phi(j)\right\} .$$

  Suppose $0<\beta<1$, and $|c(i, a)| \leqslant B$ for all $i \in X, a \in\{0,1\}$. Prove there exists a deterministic stationary Markov policy that is optimal, explaining what the italicised words mean.

  Let $F_{n}=\mathcal{L}^{n} F_{0}$, where $F_{0}=0$, and $M_{n}=\max _{i \in X}\left|F(i)-F_{n}(i)\right|$. Prove that

  $$M_{n} \leqslant \beta M_{n-1} \leqslant \beta^{n} B /(1-\beta) .$$

  Deduce that the value iteration algorithm converges to an optimal policy in a finite number of iterations.

  comment

• Paper 1, Section II, A

  Principles of Quantum Mechanics

  Part II, 2016

  A particle in one dimension has position and momentum operators $\hat{x}$ and $\hat{p}$ whose eigenstates obey

  $$\left\langle x \mid x^{\prime}\right\rangle=\delta\left(x-x^{\prime}\right), \quad\left\langle p \mid p^{\prime}\right\rangle=\delta\left(p-p^{\prime}\right), \quad\langle x \mid p\rangle=(2 \pi \hbar)^{-1 / 2} e^{i x p / \hbar}$$

  For a state $|\psi\rangle$, define the position-space and momentum-space wavefunctions $\psi(x)$ and $\tilde{\psi}(p)$ and show how each of these can be expressed in terms of the other.

  Write down the translation operator $U(\alpha)$ and check that your expression is consistent with the property $U(\alpha)|x\rangle=|x+\alpha\rangle$. For a state $|\psi\rangle$, relate the position-space and momentum-space wavefunctions for $U(\alpha)|\psi\rangle$ to $\psi(x)$ and $\tilde{\psi}(p)$ respectively.

  Now consider a harmonic oscillator with mass $m$, frequency $\omega$, and annihilation and creation operators

  $$a=\left(\frac{m \omega}{2 \hbar}\right)^{1 / 2}\left(\hat{x}+\frac{i}{m \omega} \hat{p}\right), \quad a^{\dagger}=\left(\frac{m \omega}{2 \hbar}\right)^{1 / 2}\left(\hat{x}-\frac{i}{m \omega} \hat{p}\right)$$

  Let $\psi_{n}(x)$ and $\tilde{\psi}_{n}(p)$ be the wavefunctions corresponding to the normalised energy eigenstates $|n\rangle$, where $n=0,1,2, \ldots$.

  (i) Express $\psi_{0}(x-\alpha)$ explicitly in terms of the wavefunctions $\psi_{n}(x)$.

  (ii) Given that $\tilde{\psi}_{n}(p)=f_{n}(u) \tilde{\psi}_{0}(p)$, where the $f_{n}$ are polynomials and $u=(2 / \hbar m \omega)^{1 / 2} p$, show that

  $$e^{-i \gamma u}=e^{-\gamma^{2} / 2} \sum_{n=0}^{\infty} \frac{\gamma^{n}}{\sqrt{n !}} f_{n}(u) \text { for any real } \gamma$$

  [You may quote standard results for a harmonic oscillator. You may also use, without proof, $e^{A+B}=e^{A} e^{B} e^{-\frac{1}{2}[A, B]}$ for operators $A$ and $B$ which each commute with $\left.[A, B] .\right]$

  comment

• Paper 2, Section II, A

  Applications of Quantum Mechanics

  Part II, 2016

  A particle of mass $m$ moves in three dimensions subject to a potential $V(\mathbf{r})$ localised near the origin. The wavefunction for a scattering process with incident particle of wavevector $\mathbf{k}$ is denoted $\psi(\mathbf{k}, \mathbf{r})$. With reference to the asymptotic form of $\psi$, define the scattering amplitude $f\left(\mathbf{k}, \mathbf{k}^{\prime}\right)$, where $\mathbf{k}^{\prime}$ is the wavevector of the outgoing particle with $\left|\mathbf{k}^{\prime}\right|=|\mathbf{k}|=k$.

  By recasting the Schrödinger equation for $\psi(\mathbf{k}, \mathbf{r})$ as an integral equation, show that

  $$f\left(\mathbf{k}, \mathbf{k}^{\prime}\right)=-\frac{m}{2 \pi \hbar^{2}} \int d^{3} \mathbf{r}^{\prime} \exp \left(-i \mathbf{k}^{\prime} \cdot \mathbf{r}^{\prime}\right) V\left(\mathbf{r}^{\prime}\right) \psi\left(\mathbf{k}, \mathbf{r}^{\prime}\right)$$

  [You may assume that

  $$\mathcal{G}(k ; \mathbf{r})=-\frac{1}{4 \pi|\mathbf{r}|} \exp (i k|\mathbf{r}|)$$

  is the Green's function for $\nabla^{2}+k^{2}$ which obeys the appropriate boundary conditions for a scattering solution.]

  Now suppose $V(\mathbf{r})=\lambda U(\mathbf{r})$, where $\lambda \ll 1$ is a dimensionless constant. Determine the first two non-zero terms in the expansion of $f\left(\mathbf{k}, \mathbf{k}^{\prime}\right)$ in powers of $\lambda$, giving each term explicitly as an integral over one or more position variables $\mathbf{r}, \mathbf{r}^{\prime}, \ldots$

  Evaluate the contribution to $f\left(\mathbf{k}, \mathbf{k}^{\prime}\right)$ of order $\lambda$ in the case $U(\mathbf{r})=\delta(|\mathbf{r}|-a)$, expressing the answer as a function of $a, k$ and the scattering angle $\theta$ (defined so that $\left.\mathbf{k} \cdot \mathbf{k}^{\prime}=k^{2} \cos \theta\right)$.

  comment

• Paper 3, Section II, 31 A

  Principles of Quantum Mechanics

  Part II, 2016

  A three-dimensional oscillator has Hamiltonian

  $$H=\frac{1}{2 m}\left(\hat{p}_{1}^{2}+\hat{p}_{2}^{2}+\hat{p}_{3}^{2}\right)+\frac{1}{2} m \omega^{2}\left(\alpha^{2} \hat{x}_{1}^{2}+\beta^{2} \hat{x}_{2}^{2}+\gamma^{2} \hat{x}_{3}^{2}\right),$$

  where the constants $m, \omega, \alpha, \beta, \gamma$ are real and positive. Assuming a unique ground state, construct the general normalised eigenstate of $H$ and give a formula for its energy eigenvalue. [You may quote without proof results for a one-dimensional harmonic oscillator of mass $m$ and frequency $\omega$ that follow from writing $\hat{x}=(\hbar / 2 m \omega)^{1 / 2}\left(a+a^{\dagger}\right)$ and $\left.\hat{p}=(\hbar m \omega / 2)^{1 / 2} i\left(a^{\dagger}-a\right) .\right]$

  List all states in the four lowest energy levels of $H$ in the cases:

  (i) $\alpha<\beta<\gamma<2 \alpha$;

  (ii) $\alpha=\beta$ and $\gamma=\alpha+\epsilon$, where $0<\epsilon \ll \alpha$.

  Now consider $H$ with $\alpha=\beta=\gamma=1$ subject to a perturbation

  $$\lambda m \omega^{2}\left(\hat{x}_{1} \hat{x}_{2}+\hat{x}_{2} \hat{x}_{3}+\hat{x}_{3} \hat{x}_{1}\right),$$

  where $\lambda$ is small. Compute the changes in energies for the ground state and the states at the first excited level of the original Hamiltonian, working to the leading order at which nonzero corrections occur. [You may quote without proof results from perturbation theory.]

  Explain briefly why some energy levels of the perturbed Hamiltonian will be exactly degenerate. [Hint: Compare with (ii) above.]

  comment

• Paper 4, Section II, A

  Principles of Quantum Mechanics

  Part II, 2016

  (a) Consider a quantum system with Hamiltonian $H=H_{0}+V$, where $H_{0}$ is independent of time. Define the interaction picture corresponding to this Hamiltonian and derive an expression for the time derivative of an operator in the interaction picture, assuming it is independent of time in the Schrödinger picture.

  (b) The Pauli matrices $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ satisfy

  $$\sigma_{i} \sigma_{j}=\delta_{i j}+i \epsilon_{i j k} \sigma_{k}$$

  Explain briefly how these properties allow $\sigma$ to be used to describe a quantum system with spin $\frac{1}{2}$.

  (c) A particle with spin $\frac{1}{2}$ has position and momentum operators $\hat{\mathbf{x}}=\left(\hat{x}_{1}, \hat{x}_{2}, \hat{x}_{3}\right)$ and $\hat{\mathbf{p}}=\left(\hat{p}_{1}, \hat{p}_{2}, \hat{p}_{3}\right)$. The unitary operator corresponding to a rotation through an angle $\theta$ about an axis $\mathbf{n}$ is $U=\exp (-i \theta \mathbf{n} \cdot \mathbf{J} / \hbar)$ where $\mathbf{J}$ is the total angular momentum. Check this statement by considering the effect of an infinitesimal rotation on $\hat{\mathbf{x}}, \hat{\mathbf{p}}$ and $\boldsymbol{\sigma}$.

  (d) Suppose that the particle in part (c) has Hamiltonian $H=H_{0}+V$ with

  $$H_{0}=\frac{1}{2 m} \hat{\mathbf{p}}^{2}+\alpha \mathbf{L} \cdot \boldsymbol{\sigma} \quad \text { and } \quad V=B \sigma_{3}$$

  where $\mathbf{L}$ is the orbital angular momentum and $\alpha, B$ are constants. Show that all components of $\mathbf{J}$ are independent of time in the interaction picture. Is this true in the Heisenberg picture?

  [You may quote commutation relations of $\mathbf{L}$ with $\hat{\mathbf{x}}$ and $\hat{\mathbf{p}}$.]

  comment

• Paper 2, Section II, A

  Principles of Quantum Mechanics

  Part II, 2016

  (a) Let $|j m\rangle$ be standard, normalised angular momentum eigenstates with labels specifying eigenvalues for $\mathbf{J}^{2}$ and $J_{3}$. Taking units in which $\hbar=1$,

  $$J_{\pm}|j m\rangle=\{(j \mp m)(j \pm m+1)\}^{1 / 2}|j m \pm 1\rangle .$$

  Check the coefficients above by computing norms of states, quoting any angular momentum commutation relations that you require.

  (b) Two particles, each of spin $s>0$, have combined spin states $|J M\rangle$. Find expressions for all such states with $M=2 s-1$ in terms of product states.

  (c) Suppose that the particles in part (b) move about their centre of mass with a spatial wavefunction that is a spherically symmetric function of relative position. If the particles are identical, what spin states $|J 2 s-1\rangle$ are allowed? Justify your answer.

  (d) Now consider two particles of spin 1 that are not identical and are both at rest. If the 3-component of the spin of each particle is zero, what is the probability that their total, combined spin is zero?

  comment

• Paper 3, Section II, J

  Principles of Statistics

  Part II, 2016

  Let $X_{1}, \ldots, X_{n}$ be i.i.d. random variables from a $N(\theta, 1)$ distribution, $\theta \in \mathbb{R}$, and consider a Bayesian model $\theta \sim N\left(0, v^{2}\right)$ for the unknown parameter, where $v>0$ is a fixed constant.

  (a) Derive the posterior distribution $\Pi\left(\cdot \mid X_{1}, \ldots, X_{n}\right)$ of $\theta \mid X_{1}, \ldots, X_{n}$.

  (b) Construct a credible set $C_{n} \subset \mathbb{R}$ such that

  (i) $\Pi\left(C_{n} \mid X_{1}, \ldots, X_{n}\right)=0.95$ for every $n \in \mathbb{N}$, and

  (ii) for any $\theta_{0} \in \mathbb{R}$,

  $$P_{\theta_{0}}^{\mathbb{N}}\left(\theta_{0} \in C_{n}\right) \rightarrow 0.95 \quad \text { as } n \rightarrow \infty,$$

  where $P_{\theta}^{\mathbb{N}}$ denotes the distribution of the infinite sequence $X_{1}, X_{2}, \ldots$ when drawn independently from a fixed $N(\theta, 1)$ distribution.

  [You may use the central limit theorem.]

  comment

• Paper 2, Section II,

  Principles of Statistics

  Part II, 2016

  (a) State and prove the Cramér-Rao inequality in a parametric model $\{f(\theta): \theta \in \Theta\}$, where $\Theta \subseteq \mathbb{R}$. [Necessary regularity conditions on the model need not be specified.]

  (b) Let $X_{1}, \ldots, X_{n}$ be i.i.d. Poisson random variables with unknown parameter $E X_{1}=\theta>0$. For $\bar{X}_{n}=(1 / n) \sum_{i=1}^{n} X_{i}$ and $S^{2}=(n-1)^{-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)^{2}$ define

  $$T_{\alpha}=\alpha \bar{X}_{n}+(1-\alpha) S^{2}, \quad 0 \leqslant \alpha \leqslant 1$$

  Show that $\operatorname{Var}_{\theta}\left(T_{\alpha}\right) \geqslant \operatorname{Var}_{\theta}\left(\bar{X}_{n}\right)$ for all values of $\alpha, \theta$.

  Now suppose $\tilde{\theta}=\tilde{\theta}\left(X_{1}, \ldots, X_{n}\right)$ is an estimator of $\theta$ with possibly nonzero bias $B(\theta)=E_{\theta} \tilde{\theta}-\theta$. Suppose the function $B$ is monotone increasing on $(0, \infty)$. Prove that the mean-squared errors satisfy

  $$E_{\theta}\left(\tilde{\theta}_{n}-\theta\right)^{2} \geqslant E_{\theta}\left(\bar{X}_{n}-\theta\right)^{2} \text { for all } \theta \in \Theta$$

  comment

• Paper 4, Section II, J

  Principles of Statistics

  Part II, 2016

  Consider a decision problem with parameter space $\Theta$. Define the concepts of a Bayes decision rule $\delta_{\pi}$ and of a least favourable prior.

  Suppose $\pi$ is a prior distribution on $\Theta$ such that the Bayes risk of the Bayes rule equals $\sup _{\theta \in \Theta} R\left(\delta_{\pi}, \theta\right)$, where $R(\delta, \theta)$ is the risk function associated to the decision problem. Prove that $\delta_{\pi}$ is least favourable.

  Now consider a random variable $X$ arising from the binomial distribution $\operatorname{Bin}(n, \theta)$, where $\theta \in \Theta=[0,1]$. Construct a least favourable prior for the squared risk $R(\delta, \theta)=E_{\theta}(\delta(X)-\theta)^{2}$. [You may use without proof the fact that the Bayes rule for quadratic risk is given by the posterior mean.]

  comment

• Paper 1, Section II, $\mathbf{2 7 J}$

  Principles of Statistics

  Part II, 2016

  Derive the maximum likelihood estimator $\hat{\theta}_{n}$ based on independent observations $X_{1}, \ldots, X_{n}$ that are identically distributed as $N(\theta, 1)$, where the unknown parameter $\theta$ lies in the parameter space $\Theta=\mathbb{R}$. Find the limiting distribution of $\sqrt{n}\left(\widehat{\theta}_{n}-\theta\right)$ as $n \rightarrow \infty$.

  Now define

  $$\begin{array}{rll} \tilde{\theta}_{n} & =\widehat{\theta}_{n} & \text { whenever }\left|\widehat{\theta}_{n}\right|>n^{-1 / 4}, \\ & =0 & \text { otherwise, } \end{array}$$

  $$\begin{aligned} & =0 \text { otherwise, } \end{aligned}$$

  and find the limiting distribution of $\sqrt{n}\left(\tilde{\theta}_{n}-\theta\right)$ as $n \rightarrow \infty$.

  Calculate

  $$\lim _{n \rightarrow \infty} \sup _{\theta \in \Theta} n E_{\theta}\left(T_{n}-\theta\right)^{2}$$

  for the choices $T_{n}=\widehat{\theta}_{n}$ and $T_{n}=\widetilde{\theta}_{n}$. Based on the above findings, which estimator $T_{n}$ of $\theta$ would you prefer? Explain your answer.

  [Throughout, you may use standard facts of stochastic convergence, such as the central limit theorem, provided they are clearly stated.]

  comment

• Paper 3, Section II, J

  Probability and Measure

  Part II, 2016

  (a) Define the Borel $\sigma$-algebra $\mathcal{B}$ and the Borel functions.

  (b) Give an example with proof of a set in $[0,1]$ which is not Lebesgue measurable.

  (c) The Cantor set $\mathcal{C}$ is given by

  $$\mathcal{C}=\left\{\sum_{k=1}^{\infty} \frac{a_{k}}{3^{k}}:\left(a_{k}\right) \text { is a sequence with } a_{k} \in\{0,2\} \text { for all } k\right\}$$

  (i) Explain why $\mathcal{C}$ is Lebesgue measurable.

  (ii) Compute the Lebesgue measure of $\mathcal{C}$.

  (iii) Is every subset of $\mathcal{C}$ Lebesgue measurable?

  (iv) Let $f:[0,1] \rightarrow \mathcal{C}$ be the function given by

  $$f(x)=\sum_{k=1}^{\infty} \frac{2 a_{k}}{3^{k}} \quad \text { where } \quad a_{k}=\left\lfloor 2^{k} x\right\rfloor-2\left\lfloor 2^{k-1} x\right\rfloor$$

  Explain why $f$ is a Borel function.

  (v) Using the previous parts, prove the existence of a Lebesgue measurable set which is not Borel.

  comment

• Paper 4, Section II, J

  Probability and Measure

  Part II, 2016

  Give the definitions of the convolution $f * g$ and of the Fourier transform $\widehat{f}$ of $f$, and show that $\widehat{f * g}=\widehat{f} \widehat{g}$. State what it means for Fourier inversion to hold for a function $f$.

  State the Plancherel identity and compute the $L^{2}$ norm of the Fourier transform of the function $f(x)=e^{-x} \mathbf{1}_{[0,1]}$.

  Suppose that $\left(f_{n}\right), f$ are functions in $L^{1}$ such that $f_{n} \rightarrow f$ in $L^{1}$ as $n \rightarrow \infty$. Show that $\widehat{f}_{n} \rightarrow \widehat{f}$ uniformly.

  Give the definition of weak convergence, and state and prove the Central Limit Theorem.

  comment

• Paper 2, Section II, J

  Probability and Measure

  Part II, 2016

  (a) State Jensen's inequality. Give the definition of $\|\cdot\|_{L^{p}}$ and the space $L^{p}$ for $1<p<\infty$. If $\|f-g\|_{L^{p}}=0$, is it true that $f=g$ ? Justify your answer. State and prove Hölder's inequality using Jensen's inequality.

  (b) Suppose that $(E, \mathcal{E}, \mu)$ is a finite measure space. Show that if $1<q<p$ and $f \in L^{p}(E)$ then $f \in L^{q}(E)$. Give the definition of $\|\cdot\|_{L^{\infty}}$ and show that $\|f\|_{L^{p}} \rightarrow\|f\|_{L^{\infty}}$ as $p \rightarrow \infty$.

  (c) Suppose that $1<q<p<\infty$. Show that if $f$ belongs to both $L^{p}(\mathbb{R})$ and $L^{q}(\mathbb{R})$, then $f \in L^{r}(\mathbb{R})$ for any $r \in[q, p]$. If $f \in L^{p}(\mathbb{R})$, must we have $f \in L^{q}(\mathbb{R})$ ? Give a proof or a counterexample.

  comment

• Paper 3, Section II, J

  Applied Probability

  Part II, 2016

  (a) State the thinning and superposition properties of a Poisson process on $\mathbb{R}_{+}$. Prove the superposition property.

  (b) A bi-infinite Poisson process $\left(N_{t}: t \in \mathbb{R}\right)$ with $N_{0}=0$ is a process with independent and stationary increments over $\mathbb{R}$. Moreover, for all $-\infty<s \leqslant t<\infty$, the increment $N_{t}-N_{s}$ has the Poisson distribution with parameter $\lambda(t-s)$. Prove that such a process exists.

  (c) Let $N$ be a bi-infinite Poisson process on $\mathbb{R}$ of intensity $\lambda$. We identify it with the set of points $\left(S_{n}\right)$ of discontinuity of $N$, i.e., $N[s, t]=\sum_{n} \mathbf{l}\left(S_{n} \in[s, t]\right)$. Show that if we shift all the points of $N$ by the same constant $c$, then the resulting process is also a Poisson process of intensity $\lambda$.

  Now suppose we shift every point of $N$ by $+1$ or $-1$ with equal probability. Show that the final collection of points is still a Poisson process of intensity $\lambda$. [You may assume the thinning and superposition properties for the bi-infinite Poisson process.]

  comment

• Paper 1, Section II, J

  Probability and Measure

  Part II, 2016

  Throughout this question $(E, \mathcal{E}, \mu)$ is a measure space and $\left(f_{n}\right), f$ are measurable functions.

  (a) Give the definitions of pointwise convergence, pointwise a.e. convergence, and convergence in measure.

  (b) If $f_{n} \rightarrow f$ pointwise a.e., does $f_{n} \rightarrow f$ in measure? Give a proof or a counterexample.

  (c) If $f_{n} \rightarrow f$ in measure, does $f_{n} \rightarrow f$ pointwise a.e.? Give a proof or a counterexample.

  (d) Now suppose that $(E, \mathcal{E})=([0,1], \mathcal{B}([0,1]))$ and that $\mu$ is Lebesgue measure on $[0,1]$. Suppose $\left(f_{n}\right)$ is a sequence of Borel measurable functions on $[0,1]$ which converges pointwise a.e. to $f$.

  (i) For each $n, k$ let $E_{n, k}=\bigcup_{m \geqslant n}\left\{x:\left|f_{m}(x)-f(x)\right|>1 / k\right\}$. Show that $\lim _{n \rightarrow \infty} \mu\left(E_{n, k}\right)=0$ for each $k \in \mathbb{N}$.

  (ii) Show that for every $\epsilon>0$ there exists a set $A$ with $\mu(A)<\epsilon$ so that $f_{n} \rightarrow f$ uniformly on $[0,1] \backslash A$.

  (iii) Does (ii) hold with $[0,1]$ replaced by $\mathbb{R}$ ? Give a proof or a counterexample.

  comment

• Paper 3, Section II, I

  Representation Theory

  Part II, 2016

  (a) Let the finite group $G$ act on a finite set $X$ and let $\pi$ be the permutation character. If $G$ is 2 -transitive on $X$, show that $\pi=1_{G}+\chi$, where $\chi$ is an irreducible character of $G$.

  (b) Let $n \geqslant 4$, and let $G$ be the symmetric group $S_{n}$ acting naturally on the set $X=\{1, \ldots, n\}$. For any integer $r \leqslant n / 2$, write $X_{r}$ for the set of all $r$-element subsets of $X$, and let $\pi_{r}$ be the permutation character of the action of $G$ on $X_{r}$. Compute the degree of $\pi_{r}$. If $0 \leqslant \ell \leqslant k \leqslant n / 2$, compute the character inner product $\left\langle\pi_{k}, \pi_{\ell}\right\rangle$.

  Let $m=n / 2$ if $n$ is even, and $m=(n-1) / 2$ if $n$ is odd. Deduce that $S_{n}$ has distinct irreducible characters $\chi^{(n)}=1_{G}, \chi^{(n-1,1)}, \chi^{(n-2,2)}, \ldots, \chi^{(n-m, m)}$ such that for all $r \leqslant m$,

  $$\pi_{r}=\chi^{(n)}+\chi^{(n-1,1)}+\chi^{(n-2,2)}+\cdots+\chi^{(n-r, r)}$$

  (c) Let $\Omega$ be the set of all ordered pairs $(i, j)$ with $i, j \in\{1,2, \ldots, n\}$ and $i \neq j$. Let $S_{n}$ act on $\Omega$ in the obvious way. Write $\pi^{(n-2,1,1)}$ for the permutation character of $S_{n}$ in this action. By considering inner products, or otherwise, prove that

  $$\pi^{(n-2,1,1)}=1+2 \chi^{(n-1,1)}+\chi^{(n-2,2)}+\psi$$

  where $\psi$ is an irreducible character. Calculate the degree of $\psi$, and calculate its value on the elements $\left(\begin{array}{ll}1 & 2\end{array}\right)$ and $\left(\begin{array}{lll}1 & 2 & 3)\end{array}\right)$ of $S_{n}$.

  comment

• Paper 2, Section II, I

  Representation Theory

  Part II, 2016

  Show that the 1-dimensional (complex) characters of a finite group $G$ form a group under pointwise multiplication. Denote this group by $\widehat{G}$. Show that if $g \in G$, the map $\chi \mapsto \chi(g)$ from $\widehat{G}$to $\mathbb{C}$ is a character of $\widehat{G}$, hence an element of $\widehat{G}$. What is the kernel of the $\operatorname{map} G \rightarrow \widehat{\widehat{G}}$?

  Show that if $G$ is abelian the map $G \rightarrow \widehat{\widehat{G}}$is an isomorphism. Deduce, from the structure theorem for finite abelian groups, that the groups $G$ and $\widehat{G}$are isomorphic as abstract groups.

  comment

• Paper 4, Section II, I

  Representation Theory

  Part II, 2016

  Let $N$ be a proper normal subgroup of a finite group $G$ and let $U$ be an irreducible complex representation of $G$. Show that either $U$ restricted to $N$ is a sum of copies of a single irreducible representation of $N$, or else $U$ is induced from an irreducible representation of some proper subgroup of $G$.

  Recall that a $p$-group is a group whose order is a power of the prime number $p$. Deduce, by induction on the order of the group, or otherwise, that every irreducible complex representation of a $p$-group is induced from a 1-dimensional representation of some subgroup.

  [You may assume that a non-abelian $p$-group $G$ has an abelian normal subgroup which is not contained in the centre of $G$.]

  comment

• Paper 1, Section II, I

  Representation Theory

  Part II, 2016

  Let $N$ be a normal subgroup of the finite group $G$. Explain how a (complex) representation of $G / N$ gives rise to an associated representation of $G$, and briefly describe which representations of $G$ arise this way.

  Let $G$ be the group of order 54 which is given by

  $$G=\left\langle a, b: a^{9}=b^{6}=1, b^{-1} a b=a^{2}\right\rangle$$

  Find the conjugacy classes of $G$. By observing that $N_{1}=\langle a\rangle$ and $N_{2}=\left\langle a^{3}, b^{2}\right\rangle$ are normal in $G$, or otherwise, construct the character table of $G$.

  comment

• Paper 3, Section II, H

  Riemann Surfaces

  Part II, 2016

  Let $f$ be a non-constant elliptic function with respect to a lattice $\Lambda \subset \mathbb{C}$. Let $P \subset \mathbb{C}$ be a fundamental parallelogram and let the degree of $f$ be $n$. Let $a_{1}, \ldots, a_{n}$ denote the zeros of $f$ in $P$, and let $b_{1}, \ldots, b_{n}$ denote the poles (both with possible repeats). By considering the integral (if required, also slightly perturbing $P$ )

  $$\frac{1}{2 \pi i} \int_{\partial P} z \frac{f^{\prime}(z)}{f(z)} d z$$

  show that

  $$\sum_{j=1}^{n} a_{j}-\sum_{j=1}^{n} b_{j} \in \Lambda$$

  Let $\wp(z)$ denote the Weierstrass $\wp$-function with respect to $\Lambda$. For $v, w \notin \Lambda$ with $\wp(v) \neq \wp(w)$ we set

  $$f(z)=\operatorname{det}\left(\begin{array}{ccc} 1 & 1 & 1 \\ \wp(z) & \wp(v) & \wp(w) \\ \wp^{\prime}(z) & \wp^{\prime}(v) & \wp^{\prime}(w) \end{array}\right)$$

  an elliptic function with periods $\Lambda$. Suppose $z \notin \Lambda, z-v \notin \Lambda$ and $z-w \notin \Lambda$. Prove that $f(z)=0$ if and only if $z+v+w \in \Lambda$. [You may use standard properties of the Weierstrass $\wp$-function provided they are clearly stated.]

  comment

• Paper 2, Section II, H

  Riemann Surfaces

  Part II, 2016

  Suppose that $f: \mathbb{C} / \Lambda_{1} \rightarrow \mathbb{C} / \Lambda_{2}$ is a holomorphic map of complex tori, and let $\pi_{j}$ denote the projection map $\mathbb{C} \rightarrow \mathbb{C} / \Lambda_{j}$ for $j=1,2$. Show that there is a holomorphic map $F: \mathbb{C} \rightarrow \mathbb{C}$ such that $\pi_{2} F=f \pi_{1} .$

  Prove that $F(z)=\lambda z+\mu$ for some $\lambda, \mu \in \mathbb{C}$. Hence deduce that two complex tori $\mathbb{C} / \Lambda_{1}$ and $\mathbb{C} / \Lambda_{2}$ are conformally equivalent if and only if the lattices are related by $\Lambda_{2}=\lambda \Lambda_{1}$ for some $\lambda \in \mathbb{C}^{*}$.

  comment

• Paper 1, Section II, H

  Riemann Surfaces

  Part II, 2016

  (a) Let $f: R \rightarrow S$ be a non-constant holomorphic map between Riemann surfaces. Prove that $f$ takes open sets of $R$ to open sets of $S$.

  (b) Let $U$ be a simply connected domain strictly contained in $\mathbb{C}$. Is there a conformal equivalence between $U$ and $\mathbb{C}$ ? Justify your answer.

  (c) Let $R$ be a compact Riemann surface and $A \subset R$ a discrete subset. Given a non-constant holomorphic function $f: R \backslash A \rightarrow \mathbb{C}$, show that $f(R \backslash A)$ is dense in $\mathbb{C}$.

  comment

• Paper 2, Section I, K

  Statistical Modelling

  Part II, 2016

  Define an exponential dispersion family. Prove that the range of the natural parameter, $\Theta$, is an open interval. Derive the mean and variance as a function of the log normalizing constant.

  [Hint: Use the convexity of $e^{x}$, i.e. $e^{p x+(1-p) y} \leqslant p e^{x}+(1-p) e^{y}$ for all $\left.p \in[0,1] .\right]$

  comment

• Paper 4, Section I, K

  Statistical Modelling

  Part II, 2016

  (a) Let $Y_{i}=x_{i}^{\top} \beta+\varepsilon_{i}$ where $\varepsilon_{i}$ for $i=1, \ldots, n$ are independent and identically distributed. Let $Z_{i}=I\left(Y_{i}<0\right)$ for $i=1, \ldots, n$, and suppose that these variables follow a binary regression model with the complementary log-log link function $g(\mu)=$ $\log (-\log (1-\mu))$. What is the probability density function of $\varepsilon_{1}$ ?

  (b) The Newton-Raphson algorithm can be applied to compute the MLE, $\hat{\beta}$, in certain GLMs. Starting from $\beta^{(0)}=0$, we let $\beta^{(t+1)}$ be the maximizer of the quadratic approximation of the log-likelihood $\ell(\beta ; Y)$ around $\beta^{(t)}$ :

  $$\ell(\beta ; Y) \approx \ell\left(\beta^{(t)} ; Y\right)+\left(\beta-\beta^{(t)}\right)^{\top} D \ell\left(\beta^{(t)} ; Y\right)+\left(\beta-\beta^{(t)}\right)^{\top} D^{2} \ell\left(\beta^{(t)} ; Y\right)\left(\beta-\beta^{(t)}\right),$$

  where $D \ell$ and $D^{2} \ell$ are the gradient and Hessian of the log-likelihood. What is the difference between this algorithm and Iterative Weighted Least Squares? Why might the latter be preferable?

  comment

• Paper 2, Section II, J

  Applied Probability

  Part II, 2016

  (a) Define an $M / M / \infty$ queue and write without proof its stationary distribution. State Burke's theorem for an $M / M / \infty$ queue.

  (b) Let $X$ be an $M / M / \infty$ queue with arrival rate $\lambda$ and service rate $\mu$ started from the stationary distribution. For each $t$, denote by $A_{1}(t)$ the last time before $t$ that a customer departed the queue and $A_{2}(t)$ the first time after $t$ that a customer departed the queue. If there is no arrival before time $t$, then we set $A_{1}(t)=0$. What is the limit as $t \rightarrow \infty$ of $\mathbb{E}\left[A_{2}(t)-A_{1}(t)\right]$ ? Explain.

  (c) Consider a system of $N$ queues serving a finite number $K$ of customers in the following way: at station $1 \leqslant i \leqslant N$, customers are served immediately and the service times are independent exponentially distributed with parameter $\mu_{i}$; after service, each customer goes to station $j$ with probability $p_{i j}>0$. We assume here that the system is closed, i.e., $\sum_{j} p_{i j}=1$ for all $1 \leqslant i \leqslant N$.

  Let $S=\left\{\left(n_{1}, \ldots, n_{N}\right): n_{i} \in \mathbb{N}, \sum_{i=1}^{N} n_{i}=K\right\}$ be the state space of the Markov chain. Write down its $Q$-matrix. Also write down the $Q$-matrix $R$ corresponding to the position in the network of one customer (that is, when $K=1$ ). Show that there is a unique distribution $\left(\lambda_{i}\right)_{1 \leqslant i \leqslant N}$ such that $\lambda R=0$. Show that

  $$\pi(n)=C_{N} \prod_{i=1}^{N} \frac{\lambda_{i}^{n_{i}}}{n_{i} !}, \quad n=\left(n_{1}, \ldots, n_{N}\right) \in S$$

  defines an invariant measure for the chain. Are the queue lengths independent at equilibrium?

  comment

• Paper 3, Section I, K

  Statistical Modelling

  Part II, 2016

  The $R$ command

  $>\operatorname{boxcox}($ rainfall $\sim$ month+elnino+month:elnino)

  performs a Box-Cox transform of the response at several values of the parameter $\lambda$, and produces the following plot:

  

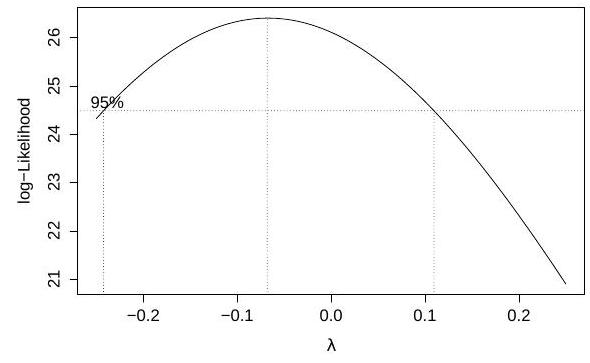
  We fit two linear models and obtain the Q-Q plots for each fit, which are shown below in no particular order:

  

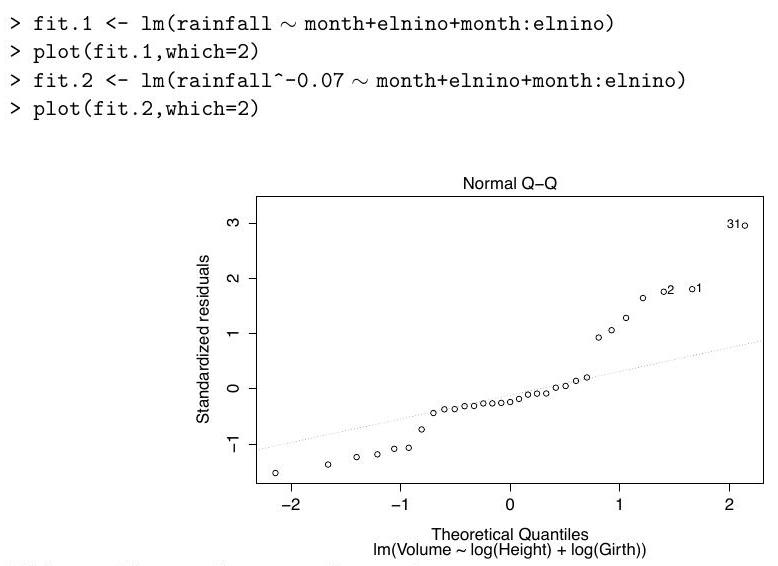
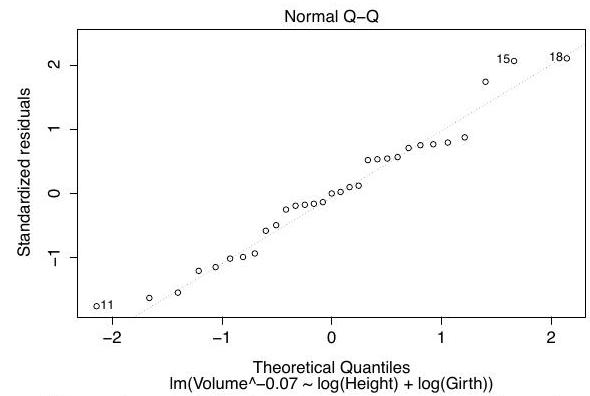
  Define the variable on the $y$-axis in the output of boxcox, and match each Q-Q plot to one of the models.

  After choosing the model fit.2, the researcher calculates Cook's distance for the $i$ th sample, which has high leverage, and compares it to the upper $0.01$-point of an $F_{p, n-p}$ distribution, because the design matrix is of size $n \times p$. Provide an interpretation of this comparison in terms of confidence sets for $\hat{\beta}$. Is this confidence statement exact?

  comment

• Paper 1, Section I, K

  Statistical Modelling

  Part II, 2016

  The body mass index (BMI) of your closest friend is a good predictor of your own BMI. A scientist applies polynomial regression to understand the relationship between these two variables among 200 students in a sixth form college. The $R$ commands

  $>$ fit. $1<-\operatorname{lm}(B M I \sim$ poly $($ friendBMI , 2, raw=T $))$

  $>$ fit. $2<-\operatorname{lm}(B M I \sim$ poly $($ friendBMI, 3, raw $=\mathrm{T}))$

  fit the models $Y=\beta_{0}+\beta_{1} X+\beta_{2} X^{2}+\varepsilon$ and $Y=\beta_{0}+\beta_{1} X+\beta_{2} X^{2}+\beta_{3} X^{3}+\varepsilon$, respectively, with $\varepsilon \sim N\left(0, \sigma^{2}\right)$ in each case.

  Setting the parameters raw to FALSE:

  $>$ fit. $3<-\operatorname{lm}(B M I \sim$ poly $($ friendBMI , 2, raw=F $)$ )

  $>$ fit. $4<-\operatorname{lm}(\mathrm{BMI} \sim$ poly $($ friendBMI, 3, raw $=\mathrm{F}))$

  fits the models $Y=\beta_{0}+\beta_{1} P_{1}(X)+\beta_{2} P_{2}(X)+\varepsilon$ and $Y=\beta_{0}+\beta_{1} P_{1}(X)+\beta_{2} P_{2}(X)+$ $\beta_{3} P_{3}(X)+\varepsilon$, with $\varepsilon \sim N\left(0, \sigma^{2}\right)$. The function $P_{i}$ is a polynomial of degree $i$. Furthermore, the design matrix output by the function poly with raw=F satisfies:

  $>t($ poly $($ friendBMI, 3, raw $=F)) \% * \%$ poly $(a, 3$, raw $=F)$

  $\begin{array}{rrrr}1 & 2 & 3 \\ 1 & 1.000000 e+00 & 1.288032 \mathrm{e}-16 & 3.187554 \mathrm{e}-17 \\ 2 & 1.288032 \mathrm{e}-16 & 1.000000 \mathrm{e}+00 & -6.201636 \mathrm{e}-17 \\ 3 & 3.187554 \mathrm{e}-17 & -6.201636 \mathrm{e}-17 & 1.000000 \mathrm{e}+00\end{array}$

  How does the variance of $\hat{\beta}$ differ in the models $f i t .2$ and $f i t .4$ ? What about the variance of the fitted values $\hat{Y}=X \hat{\beta}$ ? Finally, consider the output of the commands

  $>\operatorname{anova}$ (fit.1,fit.2)

  anova(fit.3,fit.4)

  Define the test statistic computed by this function and specify its distribution. Which command yields a higher statistic?

  comment

• Paper 4, Section II, K

  Statistical Modelling

  Part II, 2016

  For 31 days after the outbreak of the 2014 Ebola epidemic, the World Health Organization recorded the number of new cases per day in 60 hospitals in West Africa. Researchers are interested in modelling $Y_{i j}$, the number of new Ebola cases in hospital $i$ on day $j \geqslant 2$, as a function of several covariates:

  • lab: a Boolean factor for whether the hospital has laboratory facilities,

  • casesBefore: number of cases at the hospital on the previous day,

  • urban: a Boolean factor indicating an urban area,

  • country: a factor with three categories, Guinea, Liberia, and Sierra Leone,

  • numDoctors: number of doctors at the hospital,

  • tradBurials: a Boolean factor indicating whether traditional burials are common in the region.

  Consider the output of the following $R$ code (with some lines omitted):

  fit. 1 <- glm(newCases lab+casesBefore+urban+country+numDoctors+tradBurials,

  • data=ebola, family=poisson)

  $>$ summary (fit.1)

  Coefficients:

  Estimate Std. Error z value $\operatorname{Pr}(>|z|)$

  $\begin{array}{lllll}\text { labTRUE } & 0.094731 & 0.050322 & 1.882 & 0.0598 \\ \text { (Intercept) } & 0.011298 & 0.049498 & 0.228 & 0.8195\end{array}$

  casesBefore $\quad 0.324744 \quad 0.007752 \quad 41.891<2 \mathrm{e}-16 * * *$

  $\begin{array}{llllll}\text { urbanTRUE } & -0.091554 & 0.088212 & -1.038 & 0.2993\end{array}$

  countryLiberia $\quad 0.088490 \quad 0.034119 \quad 2.594 \quad 0.0095 * *$

  countrySierra Leone $-0.197474 \quad 0.036969-5.3429 .21 \mathrm{e}-08 * * *$

  numDoctors $\quad-0.020819 \quad 0.004658-4.4707 .83 \mathrm{e}-06 * * *$

  tradBurialstrUE $\quad 0.054296 \quad 0.031676 \quad 1.714 \quad 0.0865 .$

  Signif. codes: $0{ }^{\prime} * * *, 0.0011^{\prime} * *, 0.01, *, 0.05, \ldots 0.1,1$

  (a) Would you conclude based on the $z$-tests that an urban setting does not affect the rate of infection?

  (b) Explain how you would predict the total number of new cases that the researchers will record in Sierra Leone on day 32 .

  We fit a new model which includes an interaction term, and compute a test statistic using the code:

  $>$ fit. $2<-$ glm (newCases $\sim$ casesBefore+country+country:casesBefore+numDoctors,

  • data=ebola, family=poisson)

  fit. 2 deviance - fit.1$deviance

  [1] $3.016138$

  (c) What is the distribution of the statistic computed in the last line?

  (d) Under what conditions is the deviance of each model approximately chi-squared?

  comment

• Paper 1, Section II, K

  Statistical Modelling

  Part II, 2016

  (a) Let $Y$ be an $n$-vector of responses from the linear model $Y=X \beta+\varepsilon$, with $\beta \in \mathbb{R}^{p}$. The internally studentized residual is defined by

  $$s_{i}=\frac{Y_{i}-x_{i}^{\top} \hat{\beta}}{\tilde{\sigma} \sqrt{1-p_{i}}},$$

  where $\hat{\beta}$ is the least squares estimate, $p_{i}$ is the leverage of sample $i$, and

  $$\tilde{\sigma}^{2}=\frac{\|Y-X \hat{\beta}\|_{2}^{2}}{(n-p)} .$$

  Prove that the joint distribution of $s=\left(s_{1}, \ldots, s_{n}\right)^{\top}$ is the same in the following two models: (i) $\varepsilon \sim N(0, \sigma I)$, and (ii) $\varepsilon \mid \sigma \sim N(0, \sigma I)$, with $1 / \sigma \sim \chi_{\nu}^{2}$ (in this model, $\varepsilon_{1}, \ldots, \varepsilon_{n}$ are identically $t_{\nu}$-distributed). [Hint: A random vector $Z$ is spherically symmetric if for any orthogonal matrix $H, H Z \stackrel{d}{=} Z$. If $Z$ is spherically symmetric and a.s. nonzero, then $Z /\|Z\|_{2}$ is a uniform point on the sphere; in addition, any orthogonal projection of $Z$ is also spherically symmetric. A standard normal vector is spherically symmetric.]

  (b) A social scientist regresses the income of 120 Cambridge graduates onto 20 answers from a questionnaire given to the participants in their first year. She notices one questionnaire with very unusual answers, which she suspects was due to miscoding. The sample has a leverage of $0.8$. To check whether this sample is an outlier, she computes its externally studentized residual,

  $$t_{i}=\frac{Y_{i}-x_{i}^{\top} \hat{\beta}}{\tilde{\sigma}_{(i)} \sqrt{1-p_{i}}}=4.57,$$

  where $\tilde{\sigma}_{(i)}$ is estimated from a fit of all samples except the one in question, $\left(x_{i}, Y_{i}\right)$. Is this a high leverage point? Can she conclude this sample is an outlier at a significance level of $5 \%$ ?

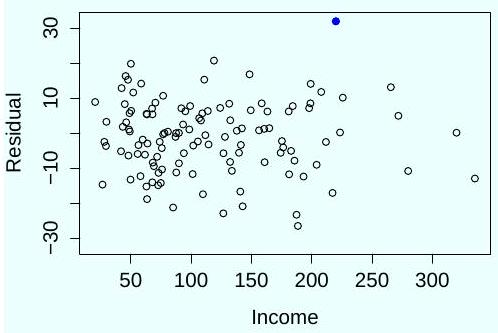
  (c) After examining the following plot of residuals against the response, the investigator calculates the externally studentized residual of the participant denoted by the black dot, which is $2.33$. Can she conclude this sample is an outlier with a significance level of $5 \%$ ?

  

  Part II, $2016 \quad$ List of Questions

  comment

• Paper 1, Section II, C

  Statistical Physics

  Part II, 2016

  Consider an ideal quantum gas with one-particle states $|i\rangle$ of energy $\epsilon_{i}$. Let $p_{i}^{\left(n_{i}\right)}$ denote the probability that state $|i\rangle$ is occupied by $n_{i}$ particles. Here, $n_{i}$ can take the values 0 or 1 for fermions and any non-negative integer for bosons. The entropy of the gas is given by

  $$S=-k_{B} \sum_{i} \sum_{n_{i}} p_{i}^{\left(n_{i}\right)} \ln p_{i}^{\left(n_{i}\right)}$$

  (a) Write down the constraints that must be satisfied by the probabilities if the average energy $\langle E\rangle$ and average particle number $\langle N\rangle$ are kept at fixed values.

  Show that if $S$ is maximised then

  $$p_{i}^{\left(n_{i}\right)}=\frac{1}{\mathcal{Z}_{i}} e^{-\left(\beta \epsilon_{i}+\gamma\right) n_{i}}$$

  where $\beta$ and $\gamma$ are Lagrange multipliers. What is $\mathcal{Z}_{i}$ ?

  (b) Insert these probabilities $p_{i}^{\left(n_{i}\right)}$ into the expression for $S$, and combine the result with the first law of thermodynamics to find the meaning of $\beta$ and $\gamma$.

  (c) Calculate the average occupation number $\left\langle n_{i}\right\rangle=\sum_{n_{i}} n_{i} p_{i}^{\left(n_{i}\right)}$ for a gas of fermions.

  comment

• Paper 3, Section II, C

  Statistical Physics

  Part II, 2016

  (a) Consider an ideal gas consisting of $N$ identical classical particles of mass $m$ moving freely in a volume $V$ with Hamiltonian $H=|\mathbf{p}|^{2} / 2 m$. Show that the partition function of the gas has the form

  $$Z_{\text {ideal }}=\frac{V^{N}}{\lambda^{3 N} N !}$$

  and find $\lambda$ as a function of the temperature $T$.

  [You may assume that $\int_{-\infty}^{\infty} e^{-a x^{2}} d x=\sqrt{\pi / a}$ for $a>0$.]

  (b) A monatomic gas of interacting particles is a modification of an ideal gas where any pair of particles with separation $r$ interact through a potential energy $U(r)$. The partition function for this gas can be written as

  $$Z=Z_{\text {ideal }}\left[1+\frac{2 \pi N}{V} \int_{0}^{\infty} f(r) r^{2} d r\right]^{N}$$

  where $f(r)=e^{-\beta U(r)}-1, \quad \beta=1 /\left(k_{B} T\right)$. The virial expansion of the equation of state for small densities $N / V$ is

  $$\frac{p}{k_{B} T}=\frac{N}{V}+B_{2}(T) \frac{N^{2}}{V^{2}}+\mathcal{O}\left(\frac{N^{3}}{V^{3}}\right)$$

  Using the free energy, show that

  $$B_{2}(T)=-2 \pi \int_{0}^{\infty} f(r) r^{2} d r$$

  (c) The Lennard-Jones potential is

  $$U(r)=\epsilon\left(\frac{r_{0}^{12}}{r^{12}}-2 \frac{r_{0}^{6}}{r^{6}}\right)$$

  where $\epsilon$ and $r_{0}$ are positive constants. Find the separation $\sigma$ where $U(\sigma)=0$ and the separation $r_{\min }$ where $U(r)$ has its minimum. Sketch the graph of $U(r)$. Calculate $B_{2}(T)$ for this potential using the approximations

  $$f(r)=e^{-\beta U(r)}-1 \simeq \begin{cases}-1 & \text { for } \quad r<\sigma \\ -\beta U(r) & \text { for } r \geqslant \sigma\end{cases}$$

  comment

• Paper 4, Section II, 33C

  Statistical Physics

  Part II, 2016

  (a) State the first law of thermodynamics. Derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial p}{\partial T}\right)_{V}$$

  (b) Consider a thermodynamic system whose energy $E$ at constant temperature $T$ is volume independent, i.e.

  $$\left(\frac{\partial E}{\partial V}\right)_{T}=0$$

  Show that this implies that the pressure has the form $p(T, V)=T f(V)$ for some function $f$.

  (c) For a photon gas inside a cavity of volume $V$, the energy $E$ and pressure $p$ are given in terms of the energy density $U$, which depends only on the temperature $T$, by

  $$E(T, V)=U(T) V, \quad p(T, V)=\frac{1}{3} U(T)$$

  Show that this implies $U(T)=\sigma T^{4}$ where $\sigma$ is a constant. Show that the entropy is

  $$S=\frac{4}{3} \sigma T^{3} V$$

  and calculate the energy $E(S, V)$ and free energy $F(T, V)$ in terms of their respective fundamental variables.

  comment

• Paper 2, Section II, C

  Statistical Physics

  Part II, 2016

  (a) What is meant by the canonical ensemble? Consider a system in the canonical ensemble that can be in states $|n\rangle, n=0,1,2, \ldots$ with energies $E_{n}$. Write down the partition function for this system and the probability $p(n)$ that the system is in state $|n\rangle$. Derive an expression for the average energy $\langle E\rangle$ in terms of the partition function.

  (b) Consider an anharmonic oscillator with energy levels

  $$\hbar \omega\left[\left(n+\frac{1}{2}\right)+\delta\left(n+\frac{1}{2}\right)^{2}\right], \quad n=0,1,2, \ldots$$

  where $\omega$ is a positive constant and $0<\delta \ll 1$ is a small constant. Let the oscillator be in contact with a reservoir at temperature $T$. Show that, to linear order in $\delta$, the partition function $Z_{1}$ for the oscillator is given by

  $$Z_{1}=\frac{c_{1}}{\sinh \frac{x}{2}}\left[1+\delta c_{2} x\left(1+\frac{2}{\sinh ^{2} \frac{x}{2}}\right)\right], \quad x=\frac{\hbar \omega}{k_{B} T}$$

  where $c_{1}$ and $c_{2}$ are constants to be determined. Also show that, to linear order in $\delta$, the average energy of a system of $N$ uncoupled oscillators of this type is given by

  $$\langle E\rangle=\frac{N \hbar \omega}{2}\left\{c_{3} \operatorname{coth} \frac{x}{2}+\delta\left[c_{4}+\frac{c_{5}}{\sinh ^{2} \frac{x}{2}}\left(1-x \operatorname{coth} \frac{x}{2}\right)\right]\right\}$$

  where $c_{3}, c_{4}, c_{5}$ are constants to be determined.

  comment

• Paper 3, Section II, K

  Stochastic Financial Models

  Part II, 2016

  Consider the following two-period market model. There is a risk-free asset which pays interest at rate $r=1 / 4$. There is also a risky stock with prices $\left(S_{t}\right)_{t \in\{0,1,2\}}$ given by

  

  The above diagram should be read as

  $$\mathbb{P}\left(S_{1}=10 \mid S_{0}=7\right)=2 / 3, \quad \mathbb{P}\left(S_{2}=14 \mid S_{1}=10\right)=1 / 2$$

  and so forth.

  (a) Find the risk-neutral probabilities.

  (b) Consider a European put option with strike $K=10$ expiring at time $T=2$. What is the initial no-arbitrage price of the option? How many shares should be held in each period to replicate the payout?

  (c) Now consider an American put option with the same strike and expiration date. Find the optimal exercise policy, assuming immediate exercise is not allowed. Would your answer change if you were allowed to exercise the option at time 0 ?

  comment

• Paper 4, Section II, K

  Stochastic Financial Models

  Part II, 2016

  Let $U$ be concave and strictly increasing, and let $\mathcal{A}$ be a vector space of random variables. For every random variable $Z$ let

  $$F(Z)=\sup _{X \in \mathcal{A}} \mathbb{E}[U(X+Z)]$$

  and suppose there exists a random variable $X_{Z} \in \mathcal{A}$ such that

  $$F(Z)=\mathbb{E}\left[U\left(X_{Z}+Z\right)\right]$$

  For a random variable $Y$, let $\pi(Y)$ be such that $F(Y-\pi(Y))=F(0)$.

  (a) Show that for every constant $a$ we have $\pi(Y+a)=\pi(Y)+a$, and that if $\mathbb{P}\left(Y_{1} \leqslant Y_{2}\right)=1$, then $\pi\left(Y_{1}\right) \leqslant \pi\left(Y_{2}\right)$. Hence show that if $\mathbb{P}(a \leqslant Y \leqslant b)=1$ for constants $a \leqslant b$, then $a \leqslant \pi(Y) \leqslant b .$

  (b) Show that $Y \mapsto \pi(Y)$ is concave, and hence show $t \mapsto \pi(t Y) / t$ is decreasing for $t>0$.

  (c) Assuming $U$ is continuously differentiable, show that $\pi(t Y) / t$ converges as $t \rightarrow 0$, and that there exists a random variable $X_{0}$ such that

  $$\lim _{t \rightarrow 0} \frac{\pi(t Y)}{t}=\frac{\mathbb{E}\left[U^{\prime}\left(X_{0}\right) Y\right]}{\mathbb{E}\left[U^{\prime}\left(X_{0}\right)\right]}$$

  comment

• Paper 4, Section II, J

  Applied Probability

  Part II, 2016

  (a) Give the definition of a renewal process. Let $\left(N_{t}\right)_{t \geqslant 0}$ be a renewal process associated with $\left(\xi_{i}\right)$ with $\mathbb{E} \xi_{1}=1 / \lambda<\infty$. Show that almost surely

  $$\frac{N_{t}}{t} \rightarrow \lambda \quad \text { as } t \rightarrow \infty$$

  (b) Give the definition of Kingman's $n$-coalescent. Let $\tau$ be the first time that all blocks have coalesced. Find an expression for $\mathbb{E} e^{-q \tau}$. Let $L_{n}$ be the total length of the branches of the tree, i.e., if $\tau_{i}$ is the first time there are $i$ lineages, then $L_{n}=$ $\sum_{i=2}^{n} i\left(\tau_{i-1}-\tau_{i}\right)$. Show that $\mathbb{E} L_{n} \sim 2 \log n$ as $n \rightarrow \infty$. Show also that $\operatorname{Var}\left(L_{n}\right) \leqslant C$ for all $n$, where $C$ is a positive constant, and that in probability

  $$\frac{L_{n}}{\mathbb{E} L_{n}} \rightarrow 1 \quad \text { as } n \rightarrow \infty$$

  comment

• Paper 2, Section II, K

  Stochastic Financial Models

  Part II, 2016

  In the context of the Black-Scholes model, let $S_{0}$ be the initial price of the stock, and let $\sigma$ be its volatility. Assume that the risk-free interest rate is zero and the stock pays no dividends. Let $\operatorname{EC}\left(S_{0}, K, \sigma, T\right)$ denote the initial price of a European call option with strike $K$ and maturity date $T$.

  (a) Show that the Black-Scholes formula can be written in the form

  $$\mathrm{EC}\left(S_{0}, K, \sigma, T\right)=S_{0} \Phi\left(d_{1}\right)-K \Phi\left(d_{2}\right)$$

  where $d_{1}$ and $d_{2}$ depend on $S_{0}, K, \sigma$ and $T$, and $\Phi$ is the standard normal distribution function.

  (b) Let $\operatorname{EP}\left(S_{0}, K, \sigma, T\right)$ be the initial price of a put option with strike $K$ and maturity $T$. Show that

  $$\operatorname{EP}\left(S_{0}, K, \sigma, T\right)=\operatorname{EC}\left(S_{0}, K, \sigma, T\right)+K-S_{0}$$

  (c) Show that

  $$\operatorname{EP}\left(S_{0}, K, \sigma, T\right)=\operatorname{EC}\left(K, S_{0}, \sigma, T\right)$$

  (d) Consider a European contingent claim with maturity $T$ and payout

  $$S_{T} I_{\left\{S_{T} \leqslant K\right\}}-K I_{\left\{S_{T}>K\right\}}$$

  Assuming $K>S_{0}$, show that its initial price can be written as $\mathrm{EC}\left(S_{0}, K, \hat{\sigma}, T\right)$ for a volatility parameter $\hat{\sigma}$ which you should express in terms of $S_{0}, K, \sigma$ and $T$.

  comment

• Paper 1, Section II, 28K

  Stochastic Financial Models

  Part II, 2016

  (a) What is a Brownian motion?

  (b) State the Brownian reflection principle. State the Cameron-Martin theorem for Brownian motion with constant drift.

  (c) Let $\left(W_{t}\right)_{t \geqslant 0}$ be a Brownian motion. Show that

  $$\mathbb{P}\left(\max _{0 \leqslant s \leqslant t}\left(W_{s}+a s\right) \leqslant b\right)=\Phi\left(\frac{b-a t}{\sqrt{t}}\right)-e^{2 a b} \Phi\left(\frac{-b-a t}{\sqrt{t}}\right)$$

  where $\Phi$ is the standard normal distribution function.

  (d) Find

  $$\mathbb{P}\left(\max _{u \geqslant t}\left(W_{u}+a u\right) \leqslant b\right)$$

  comment

• Paper 1, Section I, H

  Topics in Analysis

  Part II, 2016

  By considering the function $\mathbb{R}^{n+1} \rightarrow \mathbb{R}$ defined by

  $$R\left(a_{0}, \ldots, a_{n}\right)=\sup _{t \in[-1,1]}\left|\sum_{j=0}^{n} a_{j} t^{j}\right|$$

  or otherwise, show that there exist $K_{n}>0$ and $\delta_{n}>0$ such that

  $$K_{n} \sum_{j=0}^{n}\left|a_{j}\right| \geqslant \sup _{t \in[-1,1]}\left|\sum_{j=0}^{n} a_{j} t^{j}\right| \geqslant \delta_{n} \sum_{j=0}^{n}\left|a_{j}\right|$$

  for all $a_{j} \in \mathbb{R}, 0 \leqslant j \leqslant n$.

  Show, quoting carefully any theorems you use, that we must have $\delta_{n} \rightarrow 0$ as $n \rightarrow \infty$.

  comment

• Paper 2, Section I, H

  Topics in Analysis

  Part II, 2016

  Define what it means for a subset $E$ of $\mathbb{R}^{n}$ to be convex. Which of the following statements about a convex set $E$ in $\mathbb{R}^{n}$ (with the usual norm) are always true, and which are sometimes false? Give proofs or counterexamples as appropriate.

  (i) The closure of $E$ is convex.

  (ii) The interior of $E$ is convex.

  (iii) If $\alpha: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is linear, then $\alpha(E)$ is convex.

  (iv) If $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is continuous, then $f(E)$ is convex.

  comment

• Paper 3, Section I, $2 \mathrm{H}$

  Topics in Analysis

  Part II, 2016

  In the game of 'Chicken', $A$ and $B$ drive fast cars directly at each other. If they both swerve, they both lose 10 status points; if neither swerves, they both lose 100 status points. If one swerves and the other does not, the swerver loses 20 status points and the non-swerver gains 40 status points. Find all the pairs of probabilistic strategies such that, if one driver maintains their strategy, it is not in the interest of the other to change theirs.

  comment

• Paper 4, Section I, H

  Topics in Analysis

  Part II, 2016

  Let $a_{0}, a_{1}, a_{2}, \ldots$ be integers such that there exists an $M$ with $M \geqslant\left|a_{n}\right|$ for all $n$. Show that, if infinitely many of the $a_{n}$ are non-zero, then $\sum_{n=0}^{\infty} \frac{a_{n}}{n !}$ is an irrational number.

  comment

• Paper 2, Section II, H

  Topics in Analysis

  Part II, 2016

  Prove Bernstein's theorem, which states that if $f:[0,1] \rightarrow \mathbb{R}$ is continuous and

  $$f_{m}(t)=\sum_{r=0}^{m}\left(\begin{array}{c} m \\ r \end{array}\right) f(r / m) t^{r}(1-t)^{m-r}$$

  then $f_{m}(t) \rightarrow f(t)$ uniformly on $[0,1]$. [Theorems from probability theory may be used without proof provided they are clearly stated.]

  Deduce Weierstrass's theorem on polynomial approximation for any closed interval.

  Proving any results on Chebyshev polynomials that you need, show that, if $g:[0, \pi] \rightarrow \mathbb{R}$ is continuous and $\epsilon>0$, then we can find an $N \geqslant 0$ and $a_{j} \in \mathbb{R}$, for $0 \leqslant j \leqslant N$, such that

  $$\left|g(t)-\sum_{j=0}^{N} a_{j} \cos j t\right| \leqslant \epsilon$$

  for all $t \in[0, \pi]$. Deduce that $\int_{0}^{\pi} g(t) \cos n t d t \rightarrow 0$ as $n \rightarrow \infty$.

  comment

• Paper 4, Section II, H

  Topics in Analysis

  Part II, 2016

  Explain briefly how a positive irrational number $x$ gives rise to a continued fraction

  $$a_{0}+\frac{1}{a_{1}+\frac{1}{a_{2}+\frac{1}{a_{3}+\ldots}}}$$

  with the $a_{j}$ non-negative integers and $a_{j} \geqslant 1$ for $j \geqslant 1$.

  Show that, if we write

  $$\left(\begin{array}{ll} p_{n} & p_{n-1} \\ q_{n} & q_{n-1} \end{array}\right)=\left(\begin{array}{cc} a_{0} & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{cc} a_{1} & 1 \\ 1 & 0 \end{array}\right) \cdots\left(\begin{array}{cc} a_{n-1} & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{cc} a_{n} & 1 \\ 1 & 0 \end{array}\right)$$

  then

  $$\frac{p_{n}}{q_{n}}=a_{0}+\frac{1}{a_{1}+\frac{1}{a_{2}+\frac{1}{a_{n-1}+\frac{1}{a_{n}}}}}$$

  for $n \geqslant 0$.

  Use the observation [which need not be proved] that $x$ lies between $p_{n} / q_{n}$ and $p_{n+1} / q_{n+1}$ to show that

  $$\left|p_{n} / q_{n}-x\right| \leqslant 1 / q_{n} q_{n+1}$$

  Show that $q_{n} \geqslant F_{n}$ where $F_{n}$ is the $n$th Fibonacci number (thus $F_{0}=F_{1}=1$, $\left.F_{n+2}=F_{n+1}+F_{n}\right)$, and conclude that

  $$\left|\frac{p_{n}}{q_{n}}-x\right| \leqslant \frac{1}{F_{n} F_{n+1}}$$

  comment

• Paper 4, Section II, D

  Waves

  Part II, 2016

  A duck swims at a constant velocity $(-V, 0)$, where $V>0$, on the surface of infinitely deep water. Surface tension can be neglected, and the dispersion relation for the linear surface water waves (relative to fluid at rest) is $\omega^{2}=g|\mathbf{k}|$. Show that the wavevector $\mathbf{k}$ of a plane harmonic wave that is steady in the duck's frame, i.e. of the form

  $$\operatorname{Re}\left[A e^{i\left(k_{1} x^{\prime}+k_{2} y\right)}\right]$$

  where $x^{\prime}=x+V t$ and $y$ are horizontal coordinates relative to the duck, satisfies

  $$\left(k_{1}, k_{2}\right)=\frac{g}{V^{2}} \sqrt{p^{2}+1}(1, p)$$

  where $\hat{\mathbf{k}}=(\cos \phi, \sin \phi)$ and $p=\tan \phi$. [You may assume that $|\phi|<\pi / 2 .$ ]

  Assume that the wave pattern behind the duck can be regarded as a Fourier superposition of such steady waves, i.e., the surface elevation $\eta$ at $\left(x^{\prime}, y\right)=R(\cos \theta, \sin \theta)$ has the form

  $$\eta=\operatorname{Re} \int_{-\infty}^{\infty} A(p) e^{i \lambda h(p ; \theta)} \mathrm{d} p \quad \text { for }|\theta|<\frac{1}{2} \pi$$

  where

  $$\lambda=\frac{g R}{V^{2}}, \quad h(p ; \theta)=\sqrt{p^{2}+1}(\cos \theta+p \sin \theta)$$

  Show that, in the limit $\lambda \rightarrow \infty$ at fixed $\theta$ with $0<\theta<\cot ^{-1}(2 \sqrt{2})$,

  $$\eta \sim \sqrt{\frac{2 \pi}{\lambda}} \operatorname{Re}\left\{\frac{A\left(p_{+}\right)}{\sqrt{h_{p p}\left(p_{+} ; \theta\right)}} e^{i\left(\lambda h\left(p_{+} ; \theta\right)+\frac{1}{4} \pi\right)}+\frac{A\left(p_{-}\right)}{\sqrt{-h_{p p}\left(p_{-} ; \theta\right)}} e^{i\left(\lambda h\left(p_{-} ; \theta\right)-\frac{1}{4} \pi\right)}\right\},$$

  where

  $$p_{\pm}=-\frac{1}{4} \cot \theta \pm \frac{1}{4} \sqrt{\cot ^{2} \theta-8}$$

  and $h_{p p}$ denotes $\partial^{2} h / \partial p^{2}$. Briefly interpret this result in terms of what is seen.

  Without doing detailed calculations, briefly explain what is seen as $\lambda \rightarrow \infty$ at fixed $\theta$ with $\cot ^{-1}(2 \sqrt{2})<\theta<\pi / 2$. Very briefly comment on the case $\theta=\cot ^{-1}(2 \sqrt{2})$.

  [Hint: You may find the following results useful.

  $$\begin{gathered} h_{p}=\left\{p \cos \theta+\left(2 p^{2}+1\right) \sin \theta\right\}\left(p^{2}+1\right)^{-1 / 2} \\ \left.h_{p p}=(\cos \theta+4 p \sin \theta)\left(p^{2}+1\right)^{-1 / 2}-\left\{p \cos \theta+\left(2 p^{2}+1\right) \sin \theta\right\} p\left(p^{2}+1\right)^{-3 / 2} \cdot\right] \end{gathered}$$

  comment

• Paper 2, Section II, 37D

  Waves

  Part II, 2016

  Starting from the equations for one-dimensional unsteady flow of a perfect gas at constant entropy, show that the Riemann invariants

  $$R_{\pm}=u \pm \frac{2\left(c-c_{0}\right)}{\gamma-1}$$

  are constant on characteristics $C_{\pm}$given by $d x / d t=u \pm c$, where $u(x, t)$ is the speed of the gas, $c(x, t)$ is the local speed of sound, $c_{0}$ is a constant and $\gamma>1$ is the exponent in the adiabatic equation of state for $p(\rho)$.

  At time $t=0$ the gas occupies $x>0$ and is at rest at uniform density $\rho_{0}$, pressure $p_{0}$ and sound speed $c_{0}$. For $t>0$, a piston initially at $x=0$ has position $x=X(t)$, where

  $$X(t)=-U_{0} t\left(1-\frac{t}{2 t_{0}}\right)$$

  and $U_{0}$ and $t_{0}$ are positive constants. For the case $0<U_{0}<2 c_{0} /(\gamma-1)$, sketch the piston path $x=X(t)$ and the $C_{+}$characteristics in $x \geqslant X(t)$ in the $(x, t)$-plane, and find the time and place at which a shock first forms in the gas.

  Do likewise for the case $U_{0}>2 c_{0} /(\gamma-1)$.

  comment

• Paper 1, Section II, J

  Applied Probability

  Part II, 2016

  (a) Define a continuous-time Markov chain $X$ with infinitesimal generator $Q$ and jump chain $Y$.

  (b) Prove that if a state $x$ is transient for $Y$, then it is transient for $X$.

  (c) Prove or provide a counterexample to the following: if $x$ is positive recurrent for $X$, then it is positive recurrent for $Y$.

  (d) Consider the continuous-time Markov chain $\left(X_{t}\right)_{t \geqslant 0}$ on $\mathbb{Z}$ with non-zero transition rates given by

  $$q(i, i+1)=2 \cdot 3^{|i|}, \quad q(i, i)=-3^{|i|+1} \quad \text { and } \quad q(i, i-1)=3^{|i|}$$

  Determine whether $X$ is transient or recurrent. Let $T_{0}=\inf \left\{t \geqslant J_{1}: X_{t}=0\right\}$, where $J_{1}$ is the first jump time. Does $X$ have an invariant distribution? Justify your answer. Calculate $\mathbb{E}_{0}\left[T_{0}\right]$.

  (e) Let $X$ be a continuous-time random walk on $\mathbb{Z}^{d}$ with $q(x)=\|x\|^{\alpha} \wedge 1$ and $q(x, y)=q(x) /(2 d)$ for all $y \in \mathbb{Z}^{d}$ with $\|y-x\|=1$. Determine for which values of $\alpha$ the walk is transient and for which it is recurrent. In the recurrent case, determine the range of $\alpha$ for which it is also positive recurrent. [Here $\|x\|$ denotes the Euclidean norm of $x$.]

  comment

• Paper 1, Section II, D

  Waves

  Part II, 2016

  Write down the linearised equations governing motion of an inviscid compressible fluid at uniform entropy. Assuming that the velocity is irrotational, show that it may be derived from a velocity potential $\phi(\mathbf{x}, t)$ satisfying the wave equation

  $$\frac{\partial^{2} \phi}{\partial t^{2}}=c_{0}^{2} \nabla^{2} \phi$$

  and identify the wave speed $c_{0}$. Obtain from these linearised equations the energyconservation equation

  $$\frac{\partial E}{\partial t}+\nabla \cdot \mathbf{I}=0$$

  and give expressions for the acoustic-energy density $E$ and the acoustic-energy flux $\mathbf{I}$ in terms of $\phi$.

  Such a fluid occupies a semi-infinite waveguide $x>0$ of square cross-section $0<y<a$, $0<z<a$ bounded by rigid walls. An impenetrable membrane closing the end $x=0$ makes prescribed small displacements to

  $$x=X(y, z, t) \equiv \operatorname{Re}\left[e^{-i \omega t} A(y, z)\right]$$

  where $\omega>0$ and $|A| \ll a, c_{0} / \omega$. Show that the velocity potential is given by

  $$\phi=\operatorname{Re}\left[e^{-i \omega t} \sum_{m=0}^{\infty} \sum_{n=0}^{\infty} \cos \left(\frac{m \pi y}{a}\right) \cos \left(\frac{n \pi z}{a}\right) f_{m n}(x)\right]$$

  where the functions $f_{m n}(x)$, including their amplitudes, are to be determined, with the sign of any square roots specified clearly.

  If $0<\omega<\pi c_{0} / a$, what is the asymptotic behaviour of $\phi$ as $x \rightarrow+\infty$ ? Using this behaviour and the energy-conservation equation averaged over both time and the crosssection, or otherwise, determine the double-averaged energy flux along the waveguide,

  $$\left\langle\overline{I_{x}}\right\rangle(x) \equiv \frac{\omega}{2 \pi a^{2}} \int_{0}^{2 \pi / \omega} \int_{0}^{a} \int_{0}^{a} I_{x}(x, y, z, t) \mathrm{d} y \mathrm{~d} z \mathrm{~d} t$$

  explaining why this is independent of $x$.

  comment

• Paper 3, Section II, $37 \mathrm{D}$

  Waves

  Part II, 2016

  Small disturbances in a homogeneous elastic solid with density $\rho$ and Lamé moduli $\lambda$ and $\mu$ are governed by the equation

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+2 \mu) \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{u})-\mu \boldsymbol{\nabla} \times(\boldsymbol{\nabla} \times \mathbf{u})$$

  where $\mathbf{u}(\mathbf{x}, t)$ is the displacement. Show that a harmonic plane-wave solution

  $$\mathbf{u}=\operatorname{Re}\left[\mathbf{A} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right]$$

  must satisfy

  $$\omega^{2} \mathbf{A}=c_{P}^{2} \mathbf{k}(\mathbf{k} \cdot \mathbf{A})-c_{S}^{2} \mathbf{k} \times(\mathbf{k} \times \mathbf{A}),$$

  where the wavespeeds $c_{P}$ and $c_{S}$ are to be identified. Describe mathematically how such plane-wave solutions can be classified into longitudinal $P$-waves and transverse $S V$ - and $S H$-waves (taking the $y$-direction as the vertical direction).

  The half-space $y<0$ is filled with the elastic solid described above, while the slab $0<y<h$ is filled with a homogeneous elastic solid with Lamé moduli $\bar{\lambda}$ and $\bar{\mu}$, and wavespeeds $\bar{c}_{P}$ and $\bar{c}_{S}$. There is a rigid boundary at $y=h$. A harmonic plane $S H$-wave propagates from $y<0$ towards the interface $y=0$, with displacement

  $$\operatorname{Re}\left[A e^{i(\ell x+m y-\omega t)}\right](0,0,1)$$

  How are $\ell, m$ and $\omega$ related? The total displacement in $y<0$ is the sum of $(*)$ and that of the reflected $S H$-wave,

  $$\operatorname{Re}\left[R A e^{i(\ell x-m y-\omega t)}\right](0,0,1)$$

  Write down the form of the displacement in $0<y<h$, and determine the (complex) reflection coefficient $R$. Verify that $|R|=1$ regardless of the parameter values, and explain this physically.

  comment

• Paper 3, Section II, $37 \mathrm{D}$

  Waves

  Part II, 2016

  Small disturbances in a homogeneous elastic solid with density $\rho$ and Lamé moduli $\lambda$ and $\mu$ are governed by the equation

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+2 \mu) \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{u})-\mu \boldsymbol{\nabla} \times(\boldsymbol{\nabla} \times \mathbf{u})$$

  where $\mathbf{u}(\mathbf{x}, t)$ is the displacement. Show that a harmonic plane-wave solution

  $$\mathbf{u}=\operatorname{Re}\left[\mathbf{A} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right]$$

  must satisfy

  $$\omega^{2} \mathbf{A}=c_{P}^{2} \mathbf{k}(\mathbf{k} \cdot \mathbf{A})-c_{S}^{2} \mathbf{k} \times(\mathbf{k} \times \mathbf{A}),$$

  where the wavespeeds $c_{P}$ and $c_{S}$ are to be identified. Describe mathematically how such plane-wave solutions can be classified into longitudinal $P$-waves and transverse $S V$ - and $S H$-waves (taking the $y$-direction as the vertical direction).

  The half-space $y<0$ is filled with the elastic solid described above, while the slab $0<y<h$ is filled with a homogeneous elastic solid with Lamé moduli $\bar{\lambda}$ and $\bar{\mu}$, and wavespeeds $\bar{c}_{P}$ and $\bar{c}_{S}$. There is a rigid boundary at $y=h$. A harmonic plane $S H$-wave propagates from $y<0$ towards the interface $y=0$, with displacement

  $$\operatorname{Re}\left[A e^{i(\ell x+m y-\omega t)}\right](0,0,1)$$

  How are $\ell, m$ and $\omega$ related? The total displacement in $y<0$ is the sum of $(*)$ and that of the reflected $S H$-wave,

  $$\operatorname{Re}\left[R A e^{i(\ell x-m y-\omega t)}\right](0,0,1)$$

  Write down the form of the displacement in $0<y<h$, and determine the (complex) reflection coefficient $R$. Verify that $|R|=1$ regardless of the parameter values, and explain this physically.

  comment

• Paper 3, Section II, C

  Asymptotic Methods

  Part II, 2016

  Consider the integral

  $$I(x)=\int_{0}^{1} \frac{1}{\sqrt{t(1-t)}} \exp [i x f(t)] d t$$

  for real $x>0$, where $f(t)=t^{2}+t$. Find and sketch, in the complex $t$-plane, the paths of steepest descent through the endpoints $t=0$ and $t=1$ and through any saddle point(s). Obtain the leading order term in the asymptotic expansion of $I(x)$ for large positive $x$. What is the order of the next term in the expansion? Justify your answer.

  comment

• Paper 2, Section II, C

  Asymptotic Methods

  Part II, 2016

  What is meant by the asymptotic relation

  $$f(z) \sim g(z) \quad \text { as } \quad z \rightarrow z_{0}, \operatorname{Arg}\left(z-z_{0}\right) \in\left(\theta_{0}, \theta_{1}\right) ?$$

  Show that

  $$\sinh \left(z^{-1}\right) \sim \frac{1}{2} \exp \left(z^{-1}\right) \quad \text { as } \quad z \rightarrow 0, \operatorname{Arg} z \in(-\pi / 2, \pi / 2),$$

  and find the corresponding result in the sector $\operatorname{Arg} z \in(\pi / 2,3 \pi / 2)$.

  What is meant by the asymptotic expansion

  $$f(z) \sim \sum_{j=0}^{\infty} c_{j}\left(z-z_{0}\right)^{j} \quad \text { as } \quad z \rightarrow z_{0}, \operatorname{Arg}\left(z-z_{0}\right) \in\left(\theta_{0}, \theta_{1}\right) ?$$

  Show that the coefficients $\left\{c_{j}\right\}_{j=0}^{\infty}$ are determined uniquely by $f$. Show that if $f$ is analytic at $z_{0}$, then its Taylor series is an asymptotic expansion for $f$ as $z \rightarrow z_{0}\left(\right.$ for any $\left.\operatorname{Arg}\left(z-z_{0}\right)\right)$.

  Show that

  $$u(x, t)=\int_{-\infty}^{\infty} \exp \left(-i k^{2} t+i k x\right) f(k) d k$$

  defines a solution of the equation $i \partial_{t} u+\partial_{x}^{2} u=0$ for any smooth and rapidly decreasing function $f$. Use the method of stationary phase to calculate the leading-order behaviour of $u(\lambda t, t)$ as $t \rightarrow+\infty$, for fixed $\lambda$.

  comment

• Paper 4, Section II, C

  Asymptotic Methods

  Part II, 2016

  Consider the equation

  $$\epsilon^{2} \frac{d^{2} y}{d x^{2}}=Q(x) y$$

  where $\epsilon>0$ is a small parameter and $Q(x)$ is smooth. Search for solutions of the form

  $$y(x)=\exp \left[\frac{1}{\epsilon}\left(S_{0}(x)+\epsilon S_{1}(x)+\epsilon^{2} S_{2}(x)+\cdots\right)\right],$$

  and, by equating powers of $\epsilon$, obtain a collection of equations for the $\left\{S_{j}(x)\right\}_{j=0}^{\infty}$ which is formally equivalent to (1). By solving explicitly for $S_{0}$ and $S_{1}$ derive the Liouville- Green approximate solutions $y^{L G}(x)$ to (1).

  For the case $Q(x)=-V(x)$, where $V(x) \geqslant V_{0}$ and $V_{0}$ is a positive constant, consider the eigenvalue problem

  $$\frac{d^{2} y}{d x^{2}}+E V(x) y=0, \quad y(0)=y(\pi)=0$$

  Show that any eigenvalue $E$ is necessarily positive. Solve the eigenvalue problem exactly when $V(x)=V_{0}$.

  Obtain Liouville-Green approximate eigenfunctions $y_{n}^{L G}(x)$ for (2) with $E \gg 1$, and give the corresponding Liouville Green approximation to the eigenvalues $E_{n}^{L G}$. Compare your results to the exact eigenvalues and eigenfunctions in the case $V(x)=V_{0}$, and comment on this.

  comment

• Paper 4, Section I, $4 \mathrm{~F}$

  Automata and Formal Languages

  Part II, 2016

  (a) Construct a register machine to compute the function $f(m, n):=m+n$. State the relationship between partial recursive functions and partial computable functions. Show that the function $g(m, n):=m n$ is partial recursive.

  (b) State Rice's theorem. Show that the set $A:=\left\{n \in \mathbb{N}|| W_{n} \mid>7\right\}$ is recursively enumerable but not recursive.

  comment

• Paper 4, Section II, H

  Algebraic Geometry

  Part II, 2016

  (a) Let $C$ be a smooth projective curve, and let $D$ be an effective divisor on $C$. Explain how $D$ defines a morphism $\phi_{D}$ from $C$ to some projective space.

  State a necessary and sufficient condition on $D$ so that the pull-back of a hyperplane via $\phi_{D}$ is an element of the linear system $|D|$.

  State necessary and sufficient conditions for $\phi_{D}$ to be an isomorphism onto its image.

  (b) Let $C$ now have genus 2 , and let $K$ be an effective canonical divisor. Show that the morphism $\phi_{K}$ is a morphism of degree 2 from $C$ to $\mathbb{P}^{1}$.

  Consider the divisor $K+P_{1}+P_{2}$ for points $P_{i}$ with $P_{1}+P_{2} \nsim K$. Show that the linear system associated to this divisor induces a morphism $\phi$ from $C$ to a quartic curve in $\mathbb{P}^{2}$. Show furthermore that $\phi(P)=\phi(Q)$, with $P \neq Q$, if and only if $\{P, Q\}=\left\{P_{1}, P_{2}\right\}$.

  [You may assume the Riemann-Roch theorem.]

  comment

• Paper 3, Section I, $4 F$

  Automata and Formal Languages

  Part II, 2016

  (a) Define what it means for a context-free grammar (CFG) to be in Chomsky normal form (CNF). Can a CFG in CNF ever define a language containing $\epsilon$ ? If $G_{\text {Chom }}$ denotes the result of converting an arbitrary CFG $G$ into one in CNF, state the relationship between $\mathcal{L}(G)$ and $\mathcal{L}\left(G_{\text {Chom }}\right)$.

  (b) Let $G$ be a CFG in CNF, and let $w \in \mathcal{L}(G)$ be a word of length $|w|=n>0$. Show that every derivation of $w$ in $G$ requires precisely $2 n-1$ steps. Using this, give an algorithm that, on input of any word $v$ on the terminals of $G$, decides if $v \in \mathcal{L}(G)$ or not.

  (c) Convert the following CFG $G$ into a grammar in CNF:

  $$S \rightarrow a S b|S S| \epsilon$$

  Does $\mathcal{L}(G)=\mathcal{L}\left(G_{\text {Chom }}\right)$ in this case? Justify your answer.

  comment

• Paper 2, Section $\mathbf{I}$, $4 F$

  Automata and Formal Languages

  Part II, 2016

  (a) Which of the following are regular languages? Justify your answers.

  (i) $\left\{w \in\{a, b\}^{*} \mid w\right.$ is a nonempty string of alternating $a$ 's and $b$ 's $\}$.

  (ii) $\left\{w a b w \mid w \in\{a, b\}^{*}\right\}$.

  (b) Write down a nondeterministic finite-state automaton with $\epsilon$-transitions which accepts the language given by the regular expression $(\mathbf{a}+\mathbf{b})^{*}(\mathbf{b} \mathbf{b}+\mathbf{a}) \mathbf{b}$. Describe in words what this language is.

  (c) Is the following language regular? Justify your answer.

  $$\left\{w \in\{a, b\}^{*} \mid w \text { does not end in } a b \text { or } b b b\right\}$$

  comment

• Paper 1, Section I, $4 \mathrm{~F}$

  Automata and Formal Languages

  Part II, 2016

  State the pumping lemma for context-free languages (CFLs). Which of the following are CFLs? Justify your answers.

  (i) $\left\{a^{2 n} b^{3 n} \mid n \geqslant 3\right\}$.

  (ii) $\left\{a^{2 n} b^{3 n} c^{5 n} \mid n \geqslant 0\right\}$.

  (iii) $\left\{a^{p} \mid p\right.$ is a prime $\}$.

  Let $L, M$ be CFLs. Show that $L \cup M$ is also a CFL.

  comment

• Paper 3, Section II, F

  Automata and Formal Languages

  Part II, 2016

  (a) Let $D=\left(Q, \Sigma, \delta, q_{0}, F\right)$ be a deterministic finite-state automaton. Define the extended transition function $\hat{\delta}: Q \times \Sigma^{*} \rightarrow Q$, and the language accepted by $D$, denoted $\mathcal{L}(D)$. Let $u, v \in \Sigma^{*}$, and $p \in Q$. Prove that $\hat{\delta}(p, u v)=\hat{\delta}(\hat{\delta}(p, u), v)$.

  (b) Let $\sigma_{1}, \sigma_{2}, \ldots, \sigma_{k} \in \Sigma$ where $k \geqslant|Q|$, and let $p \in Q$.

  (i) Show that there exist $0 \leqslant i<j \leqslant k$ such that $\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{i}\right)=\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{j}\right)$, where we interpret $\sigma_{1} \cdots \sigma_{i}$ as $\epsilon$ if $i=0$.

  (ii) Show that $\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{i} \sigma_{j+1} \cdots \sigma_{k}\right)=\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{k}\right)$.

  (iii) Show that $\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{i}\left(\sigma_{i+1} \cdots \sigma_{j}\right)^{t} \sigma_{j+1} \cdots \sigma_{k}\right)=\hat{\delta}\left(p, \sigma_{1} \cdots \sigma_{k}\right)$ for all $t \geqslant 1$.

  (c) Prove the following version of the pumping lemma. Suppose $w \in \mathcal{L}(D)$, with $|w| \geqslant|Q|$. Then $w$ can be broken up into three words $w=x y z$ such that $y \neq \epsilon,|x y| \leqslant|Q|$, and for all $t \geqslant 0$, the word $x y^{t} z$ is also in $\mathcal{L}(D)$.

  (d) Hence show that

  (i) if $\mathcal{L}(D)$ contains a word of length at least $|Q|$, then it contains infinitely many words;

  (ii) if $\mathcal{L}(D) \neq \emptyset$, then it contains a word of length less than $|Q|$;

  (iii) if $\mathcal{L}(D)$ contains all words in $\Sigma^{*}$ of length less than $|Q|$, then $\mathcal{L}(D)=\Sigma^{*}$.

  comment

• Paper 1, Section II, F

  Automata and Formal Languages

  Part II, 2016

  (a) Define a recursive set and a recursively enumerable (r.e.) set. Prove that $E \subseteq \mathbb{N}$ is recursive if and only if both $E$ and $\mathbb{N} \backslash E$ are r.e.

  (b) Define the halting set $\mathbb{K}$. Prove that $\mathbb{K}$ is r.e. but not recursive.

  (c) Let $E_{1}, E_{2}, \ldots, E_{n}$ be r.e. sets. Prove that $\bigcup_{i=1}^{n} E_{i}$ and $\bigcap_{i=1}^{n} E_{i}$ are r.e. Show by an example that the union of infinitely many r.e. sets need not be r.e.

  (d) Let $E$ be a recursive set and $f: \mathbb{N} \rightarrow \mathbb{N}$ a (total) recursive function. Prove that the set $\{f(n) \mid n \in E\}$ is r.e. Is it necessarily recursive? Justify your answer.

  [Any use of Church's thesis in your answer should be explicitly stated.]

  comment

• Paper 4, Section I, E

  Classical Dynamics

  Part II, 2016

  Using conservation of angular momentum $\mathbf{L}=L_{a} \mathbf{e}_{a}$ in the body frame, derive the Euler equations for a rigid body:

  $$I_{1} \dot{\omega}_{1}+\left(I_{3}-I_{2}\right) \omega_{2} \omega_{3}=0, \quad I_{2} \dot{\omega}_{2}+\left(I_{1}-I_{3}\right) \omega_{3} \omega_{1}=0, \quad I_{3} \dot{\omega}_{3}+\left(I_{2}-I_{1}\right) \omega_{1} \omega_{2}=0$$

  [You may use the formula $\dot{\mathbf{e}}_{a}=\boldsymbol{\omega} \wedge \mathbf{e}_{a}$ without proof.]

  Assume that the principal moments of inertia satisfy $I_{1}<I_{2}<I_{3}$. Determine whether a rotation about the principal 3-axis leads to stable or unstable perturbations.

  comment

• Paper 1, Section I, E

  Classical Dynamics

  Part II, 2016

  Consider a one-parameter family of transformations $q_{i}(t) \mapsto Q_{i}(s, t)$ such that $Q_{i}(0, t)=q_{i}(t)$ for all time $t$, and

  $$\frac{\partial}{\partial s} L\left(Q_{i}, \dot{Q}_{i}, t\right)=0$$

  where $L$ is a Lagrangian and a dot denotes differentiation with respect to $t$. State and prove Noether's theorem.

  Consider the Lagrangian

  $$L=\frac{1}{2}\left(\dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2}\right)-V(x+y, y+z),$$

  where the potential $V$ is a function of two variables. Find a continuous symmetry of this Lagrangian and construct the corresponding conserved quantity. Use the Euler-Lagrange equations to explicitly verify that the function you have constructed is independent of $t$.

  comment

• Paper 2, Section I, E

  Classical Dynamics

  Part II, 2016

  Consider the Lagrangian

  $$L=A\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+B(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-C(\cos \theta)^{k}$$

  where $A, B, C$ are positive constants and $k$ is a positive integer. Find three conserved quantities and show that $u=\cos \theta$ satisfies

  $$\dot{u}^{2}=f(u)$$

  where $f(u)$ is a polynomial of degree $k+2$ which should be determined.

  comment

• Paper 3, Section I, E

  Classical Dynamics

  Part II, 2016

  Consider a six-dimensional phase space with coordinates $\left(q_{i}, p_{i}\right)$ for $i=1,2,3$. Compute the Poisson brackets $\left\{L_{i}, L_{j}\right\}$, where $L_{i}=\epsilon_{i j k} q_{j} p_{k}$.

  Consider the Hamiltonian

  $$H=\frac{1}{2}|\mathbf{p}|^{2}+V(|\mathbf{q}|)$$

  and show that the resulting Hamiltonian system admits three Poisson-commuting independent first integrals.

  comment

• Paper 2, Section II, E

  Classical Dynamics

  Part II, 2016

  Define what it means for the transformation $\mathbb{R}^{2 n} \rightarrow \mathbb{R}^{2 n}$ given by

  $$\left(q_{i}, p_{i}\right) \mapsto\left(Q_{i}\left(q_{j}, p_{j}\right), P_{i}\left(q_{j}, p_{j}\right)\right), \quad i, j=1, \ldots, n$$

  to be canonical. Show that a transformation is canonical if and only if

  $$\left\{Q_{i}, Q_{j}\right\}=0, \quad\left\{P_{i}, P_{j}\right\}=0, \quad\left\{Q_{i}, P_{j}\right\}=\delta_{i j}$$

  Show that the transformation $\mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ given by

  $$Q=q \cos \epsilon-p \sin \epsilon, \quad P=q \sin \epsilon+p \cos \epsilon$$

  is canonical for any real constant $\epsilon$. Find the corresponding generating function.

  comment

• Paper 1, Section II, H

  Algebraic Geometry

  Part II, 2016

  Let $k$ be an algebraically closed field.

  (a) Let $X$ and $Y$ be affine varieties defined over $k$. Given a map $f: X \rightarrow Y$, define what it means for $f$ to be a morphism of affine varieties.

  (b) Let $f: \mathbb{A}^{1} \rightarrow \mathbb{A}^{3}$ be the map given by

  $$f(t)=\left(t, t^{2}, t^{3}\right)$$

  Show that $f$ is a morphism. Show that the image of $f$ is a closed subvariety of $\mathbb{A}^{3}$ and determine its ideal.

  (c) Let $g: \mathbb{P}^{1} \times \mathbb{P}^{1} \times \mathbb{P}^{1} \rightarrow \mathbb{P}^{7}$ be the map given by

  $g\left(\left(s_{1}, t_{1}\right),\left(s_{2}, t_{2}\right),\left(s_{3}, t_{3}\right)\right)=\left(s_{1} s_{2} s_{3}, s_{1} s_{2} t_{3}, s_{1} t_{2} s_{3}, s_{1} t_{2} t_{3}, t_{1} s_{2} s_{3}, t_{1} s_{2} t_{3}, t_{1} t_{2} s_{3}, t_{1} t_{2} t_{3}\right) .$

  Show that the image of $g$ is a closed subvariety of $\mathbb{P}^{7}$.

  comment

• Paper 4, Section II, $14 \mathrm{E}$

  Classical Dynamics

  Part II, 2016

  A particle of unit mass is attached to one end of a light, stiff rod of length $\ell$. The other end of the rod is held at a fixed position, such that the rod is free to swing in any direction. Write down the Lagrangian for the system giving a clear definition of any angular variables you introduce. [You should assume the acceleration $g$ is constant.]

  Find two independent constants of the motion.

  The particle is projected horizontally with speed $v$ from a point where the rod lies at an angle $\alpha$ to the downward vertical, with $0<\alpha<\pi / 2$. In terms of $\ell, g$ and $\alpha$, find the critical speed $v_{c}$ such that the particle always remains at its initial height.

  The particle is now projected horizontally with speed $v_{c}$ but from a point at angle $\alpha+\delta \alpha$ to the vertical, where $\delta \alpha / \alpha \ll 1$. Show that the height of the particle oscillates, and find the period of oscillation in terms of $\ell, g$ and $\alpha$.

  comment

• Paper 1, Section I, G

  Coding and Cryptography

  Part II, 2016

  Find the average length of an optimum decipherable binary code for a source that emits five words with probabilities

  $$0.25,0.15,0.15,0.2,0.25$$

  Show that, if a source emits $N$ words (with $N \geqslant 2$ ), and if $l_{1}, \ldots, l_{N}$ are the lengths of the codewords in an optimum encoding over the binary alphabet, then

  $$l_{1}+\cdots+l_{N} \leqslant \frac{1}{2}\left(N^{2}+N-2\right) .$$

  [You may assume that an optimum encoding can be given by a Huffman encoding.]

  comment

• Paper 2, Section I, G

  Coding and Cryptography

  Part II, 2016

  Show that the binary channel with channel matrix

  $$\left(\begin{array}{ll} 1 & 0 \\ \frac{1}{2} & \frac{1}{2} \end{array}\right)$$

  has capacity $\log 5-2$.

  comment

• Paper 3, Section I, $3 G$

  Coding and Cryptography

  Part II, 2016

  Describe in words the unicity distance of a cryptosystem.

  Denote the cryptosystem by $\langle M, K, C\rangle$, in the usual way, and let $m \in M$ and $k \in K$ be random variables and $c=e(m, k)$. The unicity distance $U$ is formally defined to be the least $n>0$ such that $H\left(k \mid c^{(n)}\right)=0$. Derive the formula

  $$U=\frac{\log |K|}{\log |\Sigma|-H}$$

  where $H=H(m)$, and $\Sigma$ is the alphabet of the ciphertext. Make clear any assumptions you make.

  The redundancy of a language is given by $R=1-\frac{H}{\log |\Sigma|}$. If a language has zero redundancy what is the unicity of any cryptosystem?

  comment

• Paper 4, Section I, G

  Coding and Cryptography

  Part II, 2016

  Describe the Rabin-Williams scheme for coding a message $x$ as $x^{2}$ modulo a certain $N$. Show that, if $N$ is chosen appropriately, breaking this code is equivalent to factorising the product of two primes.

  comment

• Paper 1, Section II, G

  Coding and Cryptography

  Part II, 2016

  What does it mean to say a binary code $C$ has length $n$, size $m$ and minimum distance d?

  Let $A(n, d)$ be the largest value of $m$ for which there exists an $[n, m, d]$-code. Prove that

  $$\frac{2^{n}}{V(n, d-1)} \leqslant A(n, d) \leqslant \frac{2^{n}}{V(n,\lfloor(d-1) / 2\rfloor)}$$

  where

  $$V(n, r)=\sum_{j=0}^{r}\left(\begin{array}{l} n \\ j \end{array}\right)$$

  Another bound for $A(n, d)$ is the Singleton bound given by

  $$A(n, d) \leqslant 2^{n-d+1}$$

  Prove the Singleton bound and give an example of a linear code of length $n>1$ that satisfies $A(n, d)=2^{n-d+1}$.

  comment

• Paper 2, Section II, G

  Coding and Cryptography

  Part II, 2016

  Define a $B C H$ code of length $n$, where $n$ is odd, over the field of 2 elements with design distance $\delta$. Show that the minimum weight of such a code is at least $\delta$. [Results about the Vandermonde determinant may be quoted without proof, provided they are stated clearly.]

  Let $\omega \in \mathbb{F}_{16}$ be a root of $X^{4}+X+1$. Let $C$ be the $\mathrm{BCH}$ code of length 15 with defining set $\left\{\omega, \omega^{2}, \omega^{3}, \omega^{4}\right\}$. Find the generator polynomial of $C$ and the rank of $C$. Determine the error positions of the following received words:

  (i) $r(X)=1+X^{6}+X^{7}+X^{8}$,

  (ii) $r(X)=1+X+X^{4}+X^{5}+X^{6}+X^{9}$.

  comment

• Paper 1, Section I, C

  Cosmology

  Part II, 2016

  The expansion scale factor, $a(t)$, for an isotropic and spatially homogeneous universe containing material with pressure $p$ and mass density $\rho$ obeys the equations

  $$\begin{gathered} \dot{\rho}+3(\rho+p) \frac{\dot{a}}{a}=0, \\ \left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi G \rho}{3}-\frac{k}{a^{2}}+\frac{\Lambda}{3}, \end{gathered}$$

  where the speed of light is set equal to unity, $G$ is Newton's constant, $k$ is a constant equal to 0 or $\pm 1$, and $\Lambda$ is the cosmological constant. Explain briefly the interpretation of these equations.

  Show that these equations imply

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G(\rho+3 p)}{3}+\frac{\Lambda}{3} .$$

  Hence show that a static solution with constant $a=a_{\mathrm{s}}$ exists when $p=0$ if

  $$\Lambda=4 \pi G \rho=\frac{k}{a_{\mathrm{s}}^{2}}$$

  What must the value of $k$ be, if the density $\rho$ is non-zero?

  comment

• Paper 2, Section I, C

  Cosmology

  Part II, 2016

  A spherical cloud of mass $M$ has radius $r(t)$ and initial radius $r(0)=R$. It contains material with uniform mass density $\rho(t)$, and zero pressure. Ignoring the cosmological constant, show that if it is initially at rest at $t=0$ and the subsequent gravitational collapse is governed by Newton's law $\ddot{r}=-G M / r^{2}$, then

  $$\dot{r}^{2}=2 G M\left(\frac{1}{r}-\frac{1}{R}\right) .$$

  Suppose $r$ is given parametrically by

  $$r=R \cos ^{2} \theta$$

  where $\theta=0$ at $t=0$. Derive a relation between $\theta$ and $t$ and hence show that the cloud collapses to radius $r=0$ at

  $$t=\sqrt{\frac{3 \pi}{32 G \rho_{0}}},$$

  where $\rho_{0}$ is the initial mass density of the cloud.

  comment

• Paper 3, Section I, C

  Cosmology

  Part II, 2016

  A universe contains baryonic matter with background density $\rho_{B}(t)$ and density inhomogeneity $\delta_{B}(\mathbf{x}, t)$, together with non-baryonic dark matter with background density $\rho_{D}(t)$ and density inhomogeneity $\delta_{D}(\mathbf{x}, t)$. After the epoch of radiation-matter density equality, $t_{\mathrm{eq}}$, the background dynamics are governed by

  $$H=\frac{2}{3 t} \quad \text { and } \quad \rho_{D}=\frac{1}{6 \pi G t^{2}}$$

  where $H$ is the Hubble parameter.

  The dark-matter density is much greater than the baryonic density $\left(\rho_{D} \gg \rho_{B}\right)$ and so the time-evolution of the coupled density perturbations, at any point $\mathbf{x}$, is described by the equations

  $$\begin{aligned} &\ddot{\delta}_{B}+2 H \dot{\delta}_{B}=4 \pi G \rho_{D} \delta_{D} \\ &\ddot{\delta}_{D}+2 H \dot{\delta}_{D}=4 \pi G \rho_{D} \delta_{D} \end{aligned}$$

  Show that

  $$\delta_{D}=\frac{\alpha}{t}+\beta t^{2 / 3}$$

  where $\alpha$ and $\beta$ are independent of time. Neglecting modes in $\delta_{D}$ and $\delta_{B}$ that decay with increasing time, show that the baryonic density inhomogeneity approaches

  $$\delta_{B}=\beta t^{2 / 3}+\gamma$$

  where $\gamma$ is independent of time.

  Briefly comment on the significance of your calculation for the growth of baryonic density inhomogeneities in the early universe.

  comment

• Paper 3, Section II, G

  Algebraic Topology

  Part II, 2016

  Construct a space $X$ as follows. Let $Z_{1}, Z_{2}, Z_{3}$ each be homeomorphic to the standard 2-sphere $S^{2} \subseteq \mathbb{R}^{3}$. For each $i$, let $x_{i} \in Z_{i}$ be the North pole $(1,0,0)$ and let $y_{i} \in Z_{i}$ be the South pole $(-1,0,0)$. Then

  $$X=\left(Z_{1} \sqcup Z_{2} \sqcup Z_{3}\right) / \sim$$

  where $x_{i+1} \sim y_{i}$ for each $i$ (and indices are taken modulo 3 ).

  (a) Describe the universal cover of $X$.

  (b) Compute the fundamental group of $X$ (giving your answer as a well-known group).

  (c) Show that $X$ is not homotopy equivalent to the circle $S^{1}$.

  comment

• Paper 4, Section I, C

  Cosmology

  Part II, 2016

  The external gravitational potential $\Phi(r)$ due to a thin spherical shell of radius $a$ and mass per unit area $\sigma$, centred at $r=0$, will equal the gravitational potential due to a point mass $M$ at $r=0$, at any distance $r>a$, provided

  $$\frac{M r \Phi(r)}{2 \pi \sigma a}+K(a) r=\int_{r-a}^{r+a} R \Phi(R) d R$$

  where $K(a)$ depends on the radius of the shell. For which values of $q$ does this equation have solutions of the form $\Phi(r)=C r^{q}$, where $C$ is constant? Evaluate $K(a)$ in each case and find the relation between the mass of the shell and $M$.

  Hence show that the general gravitational force

  $$F(r)=\frac{A}{r^{2}}+B r$$

  has a potential satisfying $(*)$. What is the cosmological significance of the constant $B$ ?

  comment

• Paper 3, Section II, C

  Cosmology

  Part II, 2016

  The early universe is described by equations (with units such that $c=8 \pi G=\hbar=1$ )

  $$3 H^{2}=\rho, \quad \dot{\rho}+3 H(\rho+p)=0$$

  where $H=\dot{a} / a$. The universe contains only a self-interacting scalar field $\phi$ with interaction potential $V(\phi)$ so that the density and pressure are given by

  $$\begin{aligned} \rho &=\frac{1}{2} \dot{\phi}^{2}+V(\phi) \\ p &=\frac{1}{2} \dot{\phi}^{2}-V(\phi) . \end{aligned}$$

  Show that

  $$\ddot{\phi}+3 H \dot{\phi}+V^{\prime}(\phi)=0$$

  Explain the slow-roll approximation and apply it to equations (1) and (2) to show that it leads to

  $$\sqrt{3} \int \frac{\sqrt{V}}{V^{\prime}} d \phi=-t+\text { const. }$$

  If $V(\phi)=\frac{1}{4} \lambda \phi^{4}$ with $\lambda$ a positive constant and $\phi(0)=\phi_{0}$, show that

  $$\phi(t)=\phi_{0} \exp \left[-\sqrt{\frac{4 \lambda}{3}} t\right]$$

  and that, for small $t$, the scale factor $a(t)$ expands to leading order in $t$ as

  $$a(t) \propto \exp \left[\sqrt{\frac{\lambda}{12}} \phi_{0}^{2} t\right]$$

  Comment on the relevance of this result for inflationary cosmology.

  comment

• Paper 1, Section II, C

  Cosmology

  Part II, 2016

  The distribution function $f(\mathbf{x}, \mathbf{p}, t)$ gives the number of particles in the universe with position in $(\mathbf{x}, \mathbf{x}+\delta \mathbf{x})$ and momentum in $(\mathbf{p}, \mathbf{p}+\delta \mathbf{p})$ at time $t$. It satisfies the boundary condition that $f \rightarrow 0$ as $|\mathbf{x}| \rightarrow \infty$ and as $|\mathbf{p}| \rightarrow \infty$. Its evolution obeys the Boltzmann equation

  $$\frac{\partial f}{\partial t}+\frac{\partial f}{\partial \mathbf{p}} \cdot \frac{d \mathbf{p}}{d t}+\frac{\partial f}{\partial \mathbf{x}} \cdot \frac{d \mathbf{x}}{d t}=\left[\frac{d f}{d t}\right]_{\mathrm{col}}$$

  where the collision term $\left[\frac{d f}{d t}\right]_{c o l}$ describes any particle production and annihilation that occurs.

  The universe expands isotropically and homogeneously with expansion scale factor $a(t)$, so the momenta evolve isotropically with magnitude $p \propto a^{-1}$. Show that the Boltzmann equation simplifies to

  $$\frac{\partial f}{\partial t}-\frac{\dot{a}}{a} \mathbf{p} \cdot \frac{\partial f}{\partial \mathbf{p}}=\left[\frac{d f}{d t}\right]_{\mathrm{col}}$$

  The number densities $n$ of particles and $\bar{n}$ of antiparticles are defined in terms of their distribution functions $f$ and $\bar{f}$, and momenta $p$ and $\bar{p}$, by

  $$n=\int_{0}^{\infty} f 4 \pi p^{2} d p \quad \text { and } \quad \bar{n}=\int_{0}^{\infty} \bar{f} 4 \pi \bar{p}^{2} d \bar{p}$$

  and the collision term may be assumed to be of the form

  $$\left[\frac{d f}{d t}\right]_{\mathrm{col}}=-\langle\sigma v\rangle \int_{0}^{\infty} \bar{f} f 4 \pi \bar{p}^{2} d \bar{p}+R$$

  where $\langle\sigma v\rangle$ determines the annihilation cross-section of particles by antiparticles and $R$ is the production rate of particles.

  By integrating equation $(*)$ with respect to the momentum $\mathbf{p}$ and assuming that $\langle\sigma v\rangle$ is a constant, show that

  $$\frac{d n}{d t}+3 \frac{\dot{a}}{a} n=-\langle\sigma v\rangle n \bar{n}+Q$$

  where $Q=\int_{0}^{\infty} R 4 \pi p^{2} d p$. Assuming the same production rate $R$ for antiparticles, write down the corresponding equation satisfied by $\bar{n}$ and show that

  $$(n-\bar{n}) a^{3}=\mathrm{constant}$$

  comment

• Paper 3, Section II, G

  Differential Geometry

  Part II, 2016

  Explain what it means for an embedded surface $S$ in $\mathbf{R}^{3}$ to be minimal. What is meant by an isothermal parametrization $\phi: U \rightarrow V \subset \mathbf{R}^{3}$ of an embedded surface $V \subset \mathbf{R}^{3}$ ? Prove that if $\phi$ is isothermal then $\phi(U)$ is minimal if and only if the components of $\phi$ are harmonic functions on $U$. [You may assume the formula for the mean curvature of a parametrized embedded surface,

  $$H=\frac{e G-2 f F+g E}{2\left(E G-F^{2}\right)}$$

  where $E, F, G$ (respectively $e, f, g$ ) are the coefficients of the first (respectively second) fundamental forms.]

  Let $S$ be an embedded connected minimal surface in $\mathbf{R}^{3}$ which is closed as a subset of $\mathbf{R}^{3}$, and let $\Pi \subset \mathbf{R}^{3}$ be a plane which is disjoint from $S$. Assuming that local isothermal parametrizations always exist, show that if the Euclidean distance between $S$ and $\Pi$ is attained at some point $P \in S$, i.e. $d(P, \Pi)=\inf _{Q \in S} d(Q, \Pi)$, then $S$ is a plane parallel to 川.

  comment

• Paper 4, Section II, G

  Differential Geometry

  Part II, 2016

  For $S \subset \mathbf{R}^{3}$ a smooth embedded surface, define what is meant by a geodesic curve on $S$. Show that any geodesic curve $\gamma(t)$ has constant speed $|\dot{\gamma}(t)|$.

  For any point $P \in S$, show that there is a parametrization $\phi: U \rightarrow V$ of some open neighbourhood $V$ of $P$ in $S$, with $U \subset \mathbf{R}^{2}$ having coordinates $(u, v)$, for which the first fundamental form is

  $$d u^{2}+G(u, v) d v^{2}$$

  for some strictly positive smooth function $G$ on $U$. State a formula for the Gaussian curvature $K$ of $S$ in $V$ in terms of $G$. If $K \equiv 0$ on $V$, show that $G$ is a function of $v$ only, and that we may reparametrize so that the metric is locally of the form $d u^{2}+d w^{2}$, for appropriate local coordinates $(u, w)$.

  [You may assume that for any $P \in S$ and nonzero $\xi \in T_{P} S$, there exists (for some $\epsilon>0)$ a unique geodesic $\gamma:(-\epsilon, \epsilon) \rightarrow S$ with $\gamma(0)=P$ and $\dot{\gamma}(0)=\xi$, and that such geodesics depend smoothly on the initial conditions $P$ and $\xi .]$

  comment

• Paper 2, Section II, G

  Differential Geometry

  Part II, 2016

  If an embedded surface $S \subset \mathbf{R}^{3}$ contains a line $L$, show that the Gaussian curvature is non-positive at each point of $L$. Give an example where the Gaussian curvature is zero at each point of $L$.

  Consider the helicoid $S$ given as the image of $\mathbf{R}^{2}$ in $\mathbf{R}^{3}$ under the map

  $$\phi(u, v)=(\sinh v \cos u, \sinh v \sin u, u) .$$

  What is the image of the corresponding Gauss map? Show that the Gaussian curvature at a point $\phi(u, v) \in S$ is given by $-1 / \cosh ^{4} v$, and hence is strictly negative everywhere. Show moreover that there is a line in $S$ passing through any point of $S$.

  [General results concerning the first and second fundamental forms on an oriented embedded surface $S \subset \mathbf{R}^{3}$ and the Gauss map may be used without proof in this question.]

  comment

• Paper 1, Section II, G

  Differential Geometry

  Part II, 2016

  Define what is meant by the regular values and critical values of a smooth map $f: X \rightarrow Y$ of manifolds. State the Preimage Theorem and Sard's Theorem.

  Suppose now that $\operatorname{dim} X=\operatorname{dim} Y$. If $X$ is compact, prove that the set of regular values is open in $Y$, but show that this may not be the case if $X$ is non-compact.

  Construct an example with $\operatorname{dim} X=\operatorname{dim} Y$ and $X$ compact for which the set of critical values is not a submanifold of $Y$.

  [Hint: You may find it helpful to consider the case $X=S^{1}$ and $Y=\mathbf{R}$. Properties of bump functions and the function $e^{-1 / x^{2}}$ may be assumed in this question.]

  comment

• Paper 3, Section II, E

  Dynamical Systems

  Part II, 2016

  Consider the dependence of the system

  $$\begin{aligned} \dot{x} &=\left(a-x^{2}\right)\left(a^{2}-y\right) \\ \dot{y} &=x-y \end{aligned}$$

  on the parameter $a$. Find the fixed points and plot their location in the $(a, x)$-plane. Hence, or otherwise, deduce that there are bifurcations at $a=0$ and $a=1$.

  Investigate the bifurcation at $a=1$ by making the substitutions $u=x-1, v=y-1$ and $\mu=a-1$. Find the extended centre manifold in the form $v(u, \mu)$ correct to second order. Find the evolution equation on the extended centre manifold to second order, and determine the stability of its fixed points.

  Use a plot to show which branches of fixed points in the $(a, x)$-plane are stable and which are unstable, and state, without calculation, the type of bifurcation at $a=0$. Hence sketch the structure of the $(x, y)$ phase plane very close to the origin for $|a| \ll 1$ in the cases (i) $a<0$ and (ii) $a>0$.

  comment

• Paper 1, Section II, E

  Dynamical Systems

  Part II, 2016

  Consider the dynamical system

  $$\begin{aligned} &\dot{x}=x(y-a), \\ &\dot{y}=1-x-y^{2}, \end{aligned}$$

  where $-1<a<1$. Find and classify the fixed points of the system.

  Use Dulac's criterion with a weighting function of the form $\phi=x^{p}$ and a suitable choice of $p$ to show that there are no periodic orbits for $a \neq 0$. For the case $a=0$ use the same weighting function to find a function $V(x, y)$ which is constant on trajectories. [Hint: $\phi \dot{\mathbf{x}}$ is Hamiltonian.]

  Calculate the stable manifold at $(0,-1)$ correct to quadratic order in $x$.

  Sketch the phase plane for the cases (i) $a=0$ and (ii) $a=\frac{1}{2}$.

  comment

• Paper 4, Section II, E

  Dynamical Systems

  Part II, 2016

  Consider the map defined on $\mathbb{R}$ by

  $$F(x)= \begin{cases}3 x & x \leqslant \frac{1}{2} \\ 3(1-x) & x \geqslant \frac{1}{2}\end{cases}$$

  and let $I$ be the open interval $(0,1)$. Explain what it means for $F$ to have a horseshoe on $I$ by identifying the relevant intervals in the definition.

  Let $\Lambda=\left\{x: F^{n}(x) \in I, \forall n \geqslant 0\right\}$. Show that $F(\Lambda)=\Lambda$.

  Find the sets $\Lambda_{1}=\{x: F(x) \in I\}$ and $\Lambda_{2}=\left\{x: F^{2}(x) \in I\right\}$.

  Consider the ternary (base-3) representation $x=0 \cdot x_{1} x_{2} x_{3} \ldots$ of numbers in $I$. Show that

  $$F\left(0 \cdot x_{1} x_{2} x_{3} \ldots\right)=\left\{\begin{array}{ll} x_{1} \cdot x_{2} x_{3} x_{4} \ldots & x \leqslant \frac{1}{2} \\ \sigma\left(x_{1}\right) \cdot \sigma\left(x_{2}\right) \sigma\left(x_{3}\right) \sigma\left(x_{4}\right) \ldots & x \geqslant \frac{1}{2} \end{array},\right.$$

  where the function $\sigma\left(x_{i}\right)$ of the ternary digits should be identified. What is the ternary representation of the non-zero fixed point? What do the ternary representations of elements of $\Lambda$ have in common?

  Show that $F$ has sensitive dependence on initial conditions on $\Lambda$, that $F$ is topologically transitive on $\Lambda$, and that periodic points are dense in $\Lambda$. [Hint: You may assume that $F^{n}\left(0 \cdot x_{1} \ldots x_{n-1} 0 x_{n+1} x_{n+2} \ldots\right)=0 \cdot x_{n+1} x_{n+2} \ldots$ for $x \in \Lambda$.]

  Briefly state the relevance of this example to the relationship between Glendinning's and Devaney's definitions of chaos.

  comment

• Paper 2, Section II, G

  Algebraic Topology

  Part II, 2016

  (a) Let $K, L$ be simplicial complexes, and $f:|K| \rightarrow|L|$ a continuous map. What does it mean to say that $g: K \rightarrow L$ is a simplicial approximation to $f ?$

  (b) Define the barycentric subdivision of a simplicial complex $K$, and state the Simplicial Approximation Theorem.

  (c) Show that if $g$ is a simplicial approximation to $f$ then $f \simeq|g|$.

  (d) Show that the natural inclusion $\left|K^{(1)}\right| \rightarrow|K|$ induces a surjective map on fundamental groups.

  comment

• Paper 2, Section II, E

  Dynamical Systems

  Part II, 2016

  Consider the nonlinear oscillator

  $$\begin{aligned} \dot{x} &=y-\mu x\left(\frac{1}{2}|x|-1\right), \\ \dot{y} &=-x \end{aligned}$$

  (a) Use the Hamiltonian for $\mu=0$ to find a constraint on the size of the domain of stability of the origin when $\mu<0$.

  (b) Assume that given $\mu>0$ there exists an $R$ such that all trajectories eventually remain within the region $|\mathbf{x}| \leqslant R$. Show that there must be a limit cycle, stating carefully any result that you use. [You need not show that there is only one periodic orbit.]

  (c) Use the energy-balance method to find the approximate amplitude of the limit cycle for $0<\mu \ll 1$.

  (d) Find the approximate shape of the limit cycle for $\mu \gg 1$, and calculate the leading-order approximation to its period.

  comment

• Paper 1, Section II, E

  Electrodynamics

  Part II, 2016

  A point particle of charge $q$ and mass $m$ moves in an electromagnetic field with 4 -vector potential $A_{\mu}(x)$, where $x^{\mu}$ is position in spacetime. Consider the action

  $$S=-m c \int\left(-\eta_{\mu \nu} \frac{d x^{\mu}}{d \lambda} \frac{d x^{\nu}}{d \lambda}\right)^{1 / 2} d \lambda+q \int A_{\mu} \frac{d x^{\mu}}{d \lambda} d \lambda$$

  where $\lambda$ is an arbitrary parameter along the particle's worldline and $\eta_{\mu \nu}=\operatorname{diag}(-1,+1,+1,+1)$ is the Minkowski metric.

  (a) By varying the action with respect to $x^{\mu}(\lambda)$, with fixed endpoints, obtain the equation of motion

  $$m \frac{d u^{\mu}}{d \tau}=q F_{\nu}^{\mu} u^{\nu} \text {, }$$

  where $\tau$ is the proper time, $u^{\mu}=d x^{\mu} / d \tau$ is the velocity 4-vector, and $F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}$ is the field strength tensor.

  (b) This particle moves in the field generated by a second point charge $Q$ that is held at rest at the origin of some inertial frame. By choosing a suitable expression for $A_{\mu}$ and expressing the first particle's spatial position in spherical polar coordinates $(r, \theta, \phi)$, show from the action $(*)$ that

  $$\begin{aligned} \mathcal{E} & \equiv \dot{t}-\Gamma / r \\ \ell c & \equiv r^{2} \dot{\phi} \sin ^{2} \theta \end{aligned}$$

  are constants, where $\Gamma=-q Q /\left(4 \pi \epsilon_{0} m c^{2}\right)$ and overdots denote differentiation with respect to $\tau$.

  (c) Show that when the motion is in the plane $\theta=\pi / 2$,

  $$\mathcal{E}+\frac{\Gamma}{r}=\sqrt{1+\frac{\dot{r}^{2}}{c^{2}}+\frac{\ell^{2}}{r^{2}}}$$

  Hence show that the particle's orbit is bounded if $\mathcal{E}<1$, and that the particle can reach the origin in finite proper time if $\Gamma>|\ell|$.

  comment

• Paper 3, Section II, E

  Electrodynamics

  Part II, 2016

  The current density in an antenna lying along the $z$-axis takes the form

  $$\mathbf{J}(t, \mathbf{x})=\left\{\begin{array}{ll} \hat{\mathbf{z}} I_{0} \sin (k d-k|z|) e^{-i \omega t} \delta(x) \delta(y) & |z| \leqslant d \\ \mathbf{0} & |z|>d \end{array},\right.$$

  where $I_{0}$ is a constant and $\omega=c k$. Show that at distances $r=|\mathbf{x}|$ for which both $r \gg d$ and $r \gg k d^{2} /(2 \pi)$, the retarded vector potential in Lorenz gauge is

  $$\mathbf{A}(t, \mathbf{x}) \approx \hat{\mathbf{z}} \frac{\mu_{0} I_{0}}{4 \pi r} e^{-i \omega(t-r / c)} \int_{-d}^{d} \sin \left(k d-k\left|z^{\prime}\right|\right) e^{-i k z^{\prime} \cos \theta} d z^{\prime}$$

  where $\cos \theta=\hat{\mathbf{r}} \cdot \hat{\mathbf{z}}$ and $\hat{\mathbf{r}}=\mathbf{x} /|\mathbf{x}|$. Evaluate the integral to show that

  $$\mathbf{A}(t, \mathbf{x}) \approx \hat{\mathbf{z}} \frac{\mu_{0} I_{0}}{2 \pi k r}\left(\frac{\cos (k d \cos \theta)-\cos (k d)}{\sin ^{2} \theta}\right) e^{-i \omega(t-r / c)}$$

  In the far-field, where $k r \gg 1$, the electric and magnetic fields are given by

  $$\begin{aligned} &\mathbf{E}(t, \mathbf{x}) \approx-i \omega \hat{\mathbf{r}} \times[\hat{\mathbf{r}} \times \mathbf{A}(t, \mathbf{x})] \\ &\mathbf{B}(t, \mathbf{x}) \approx i k \hat{\mathbf{r}} \times \mathbf{A}(t, \mathbf{x}) \end{aligned}$$

  By calculating the Poynting vector, show that the time-averaged power radiated per unit solid angle is

  $$\frac{d \mathcal{P}}{d \Omega}=\frac{c \mu_{0} I_{0}^{2}}{8 \pi^{2}}\left(\frac{\cos (k d \cos \theta)-\cos (k d)}{\sin \theta}\right)^{2}$$

  [You may assume that in Lorenz gauge, the retarded potential due to a localised current distribution is

  $$\mathbf{A}(t, \mathbf{x})=\frac{\mu_{0}}{4 \pi} \int \frac{\mathbf{J}\left(t_{\mathrm{ret}}, \mathbf{x}^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|} d^{3} \mathbf{x}^{\prime}$$

  where the retarded time $\left.t_{\text {ret }}=t-\left|\mathbf{x}-\mathbf{x}^{\prime}\right| / c .\right]$

  comment

• Paper 4, Section II, E

  Electrodynamics

  Part II, 2016

  (a) A uniform, isotropic dielectric medium occupies the half-space $z>0$. The region $z<0$ is in vacuum. State the boundary conditions that should be imposed on $\mathbf{E}, \mathbf{D}, \mathbf{B}$ and $\mathbf{H}$ at $z=0$.

  (b) A linearly polarized electromagnetic plane wave, with magnetic field in the $(x, y)$-plane, is incident on the dielectric from $z<0$. The wavevector $\mathbf{k}$ makes an acute angle $\theta_{I}$ to the normal $\hat{\mathbf{z}}$. If the dielectric has frequency-independent relative permittivity $\epsilon_{r}$, show that the fraction of the incident power that is reflected is

  $$\mathcal{R}=\left(\frac{n \cos \theta_{I}-\cos \theta_{T}}{n \cos \theta_{I}+\cos \theta_{T}}\right)^{2}$$

  where $n=\sqrt{\epsilon_{r}}$, and the angle $\theta_{T}$ should be specified. [You should ignore any magnetic response of the dielectric.]

  (c) Now suppose that the dielectric moves at speed $\beta c$ along the $x$-axis, the incident angle $\theta_{I}=0$, and the magnetic field of the incident radiation is along the $y$-direction. Show that the reflected radiation propagates normal to the surface $z=0$, has the same frequency as the incident radiation, and has magnetic field also along the $y$-direction. [Hint: You may assume that under a standard Lorentz boost with speed $v=\beta c$ along the $x$-direction, the electric and magnetic field components transform as

  $$\left(\begin{array}{c} E_{x}^{\prime} \\ E_{y}^{\prime} \\ E_{z}^{\prime} \end{array}\right)=\left(\begin{array}{c} E_{x} \\ \gamma\left(E_{y}-v B_{z}\right) \\ \gamma\left(E_{z}+v B_{y}\right) \end{array}\right) \quad \text { and } \quad\left(\begin{array}{c} B_{x}^{\prime} \\ B_{y}^{\prime} \\ B_{z}^{\prime} \end{array}\right)=\left(\begin{array}{c} B_{x} \\ \gamma\left(B_{y}+v E_{z} / c^{2}\right) \\ \gamma\left(B_{z}-v E_{y} / c^{2}\right) \end{array}\right)$$

  where $\gamma=\left(1-\beta^{2}\right)^{-1 / 2}$.]

  (d) Show that the fraction of the incident power reflected from the moving dielectric

  $$\mathcal{R}_{\beta}=\left(\frac{n / \gamma-\sqrt{1-\beta^{2} / n^{2}}}{n / \gamma+\sqrt{1-\beta^{2} / n^{2}}}\right)^{2}$$

  comment

• Paper 4 , Section II, B

  Fluid Dynamics II

  Part II, 2016

  A thin layer of fluid of viscosity $\mu$ occupies the gap between a rigid flat plate at $y=0$ and a flexible no-slip boundary at $y=h(x, t)$. The flat plate moves with constant velocity $U \mathbf{e}_{x}$ and the flexible boundary moves with no component of velocity in the $x$-direction.

  State the two-dimensional lubrication equations governing the dynamics of the thin layer of fluid. Given a pressure gradient $\mathrm{d} p / \mathrm{d} x$, solve for the velocity profile $u(x, y, t)$ in the fluid and calculate the flux $q(x, t)$. Deduce that the pressure gradient satisfies

  $$\frac{\partial}{\partial x}\left(\frac{h^{3}}{12 \mu} \frac{\mathrm{d} p}{\mathrm{~d} x}\right)=\frac{\partial h}{\partial t}+\frac{U}{2} \frac{\partial h}{\partial x}$$

  The shape of the flexible boundary is a periodic travelling wave, i.e. $h(x, t)=$ $h(x-c t)$ and $h(\xi+L)=h(\xi)$, where $c$ and $L$ are constants. There is no applied average pressure gradient, so the pressure is also periodic with $p(\xi+L)=p(\xi)$. Show that

  $$\frac{\mathrm{d} p}{\mathrm{~d} x}=6 \mu(U-2 c)\left(\frac{1}{h^{2}}-\frac{\left\langle h^{-2}\right\rangle}{\left\langle h^{-3}\right\rangle} \frac{1}{h^{3}}\right)$$

  where $\langle\ldots\rangle=\frac{1}{L} \int_{0}^{L} \ldots \mathrm{d} x$ denotes the average over a period. Calculate the shear stress $\sigma_{x y}$ on the plate.

  The speed $U$ is such that there is no need to apply an external tangential force to the plate in order to maintain its motion. Show that

  $$U=6 c \frac{\left\langle h^{-2}\right\rangle\left\langle h^{-2}\right\rangle-\left\langle h^{-1}\right\rangle\left\langle h^{-3}\right\rangle}{3\left\langle h^{-2}\right\rangle\left\langle h^{-2}\right\rangle-4\left\langle h^{-1}\right\rangle\left\langle h^{-3}\right\rangle} .$$

  comment

• Paper 3, Section II, B

  Fluid Dynamics II

  Part II, 2016

  A cylindrical pipe of radius $a$ and length $L \gg a$ contains two viscous fluids arranged axisymmetrically with fluid 1 of viscosity $\mu_{1}$ occupying the central region $r<\beta a$, where $0<\beta<1$, and fluid 2 of viscosity $\mu_{2}$ occupying the surrounding annular region $\beta a<r<a$. The flow in each fluid is assumed to be steady and unidirectional, with velocities $u_{1}(r) \mathbf{e}_{z}$ and $u_{2}(r) \mathbf{e}_{z}$ respectively, with respect to cylindrical coordinates $(r, \theta, z)$ aligned with the pipe. A fixed pressure drop $\Delta p$ is applied between the ends of the pipe.

  Starting from the Navier-Stokes equations, derive the equations satisfied by $u_{1}(r)$ and $u_{2}(r)$, and state all the boundary conditions. Show that the pressure gradient is constant.

  Solve for the velocity profile in each fluid and calculate the corresponding flow rates, $Q_{1}$ and $Q_{2}$.

  Derive the relationship between $\beta$ and $\mu_{2} / \mu_{1}$ that yields the same flow rate in each fluid. Comment on the behaviour of $\beta$ in the limits $\mu_{2} / \mu_{1} \gg 1$ and $\mu_{2} / \mu_{1} \ll 1$, illustrating your comment by sketching the flow profiles.

  $[$ Hint: In cylindrical coordinates $(r, \theta, z)$,

  $$\nabla^{2} u=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial u}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} u}{\partial \theta^{2}}+\frac{\partial^{2} u}{\partial z^{2}}, \quad e_{r z}=\frac{1}{2}\left(\frac{\partial u_{r}}{\partial z}+\frac{\partial u_{z}}{\partial r}\right)$$

  comment

• Paper 2, Section II, B

  Fluid Dynamics II

  Part II, 2016

  For a two-dimensional flow in plane polar coordinates $(r, \theta)$, state the relationship between the streamfunction $\psi(r, \theta)$ and the flow components $u_{r}$ and $u_{\theta}$. Show that the vorticity $\omega$ is given by $\omega=-\nabla^{2} \psi$, and deduce that the streamfunction for a steady two-dimensional Stokes flow satisfies the biharmonic equation

  $$\nabla^{4} \psi=0$$

  A rigid stationary circular disk of radius $a$ occupies the region $r \leqslant a$. The flow far from the disk tends to a steady straining flow $\mathbf{u}_{\infty}=(-E x, E y)$, where $E$ is a constant. Inertial forces may be neglected. Calculate the streamfunction, $\psi_{\infty}(r, \theta)$, for the far-field flow.

  By making an appropriate assumption about its dependence on $\theta$, find the streamfunction $\psi$ for the flow around the disk, and deduce the flow components, $u_{r}(r, \theta)$ and $u_{\theta}(r, \theta)$.

  Calculate the tangential surface stress, $\sigma_{r \theta}$, acting on the boundary of the disk.

  $[$ Hints: In plane polar coordinates $(r, \theta)$,

  $$\begin{gathered} \boldsymbol{\nabla} \cdot \mathbf{u}=\frac{1}{r} \frac{\partial\left(r u_{r}\right)}{\partial r}+\frac{1}{r} \frac{\partial u_{\theta}}{\partial \theta}, \quad \omega=\frac{1}{r} \frac{\partial\left(r u_{\theta}\right)}{\partial r}-\frac{1}{r} \frac{\partial u_{r}}{\partial \theta} \\ \nabla^{2} V=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial V}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} V}{\partial \theta^{2}}, \quad e_{r \theta}=\frac{1}{2}\left(r \frac{\partial}{\partial r}\left(\frac{u_{\theta}}{r}\right)+\frac{1}{r} \frac{\partial u_{r}}{\partial \theta}\right) \end{gathered}$$

  comment

• Paper 1, Section II, B

  Fluid Dynamics II

  Part II, 2016

  State the vorticity equation and interpret the meaning of each term.

  A planar vortex sheet is diffusing in the presence of a perpendicular straining flow. The flow is everywhere of the form $\mathbf{u}=(U(y, t),-E y, E z)$, where $U \rightarrow \pm U_{0}$ as $y \rightarrow \pm \infty$, and $U_{0}$ and $E>0$ are constants. Show that the vorticity has the form $\boldsymbol{\omega}=\omega(y, t) \mathbf{e}_{z}$, and obtain a scalar equation describing the evolution of $\omega$.

  Explain physically why the solution approaches a steady state in which the vorticity is concentrated near $y=0$. Use scaling to estimate the thickness $\delta$ of the steady vorticity layer as a function of $E$ and the kinematic viscosity $\nu$.

  Determine the steady vorticity profile, $\omega(y)$, and the steady velocity profile, $U(y)$.

  $\left[\right.$ Hint: $\left.\quad \operatorname{erf}(x)=\frac{2}{\sqrt{\pi}} \int_{0}^{x} e^{-u^{2}} \mathrm{~d} u .\right]$

  State, with a brief physical justification, why you might expect this steady flow to be unstable to long-wavelength perturbations, defining what you mean by long.

  comment

• Paper 4, Section I, 7A

  Further Complex Methods

  Part II, 2016

  Consider the equation for $w(z)$ :

  $$w^{\prime \prime}+p(z) w^{\prime}+q(z) w=0 .$$

  State necessary and sufficient conditions on $p(z)$ and $q(z)$ for $z=0$ to be (i) an ordinary point or (ii) a regular singular point. Derive the corresponding conditions for the point $z=\infty$.

  Determine the most general equation of the form $(*)$ that has regular singular points at $z=0$ and $z=\infty$, with all other points being ordinary.

  comment

• Paper 3, Section I, A

  Further Complex Methods

  Part II, 2016

  The functions $f(x)$ and $g(x)$ have Laplace transforms $F(p)$ and $G(p)$ respectively, and $f(x)=g(x)=0$ for $x \leqslant 0$. The convolution $h(x)$ of $f(x)$ and $g(x)$ is defined by

  $$h(x)=\int_{0}^{x} f(y) g(x-y) d y \quad \text { for } \quad x>0 \quad \text { and } \quad h(x)=0 \quad \text { for } \quad x \leqslant 0$$

  Express the Laplace transform $H(p)$ of $h(x)$ in terms of $F(p)$ and $G(p)$.

  Now suppose that $f(x)=x^{\alpha}$ and $g(x)=x^{\beta}$ for $x>0$, where $\alpha, \beta>-1$. Find expressions for $F(p)$ and $G(p)$ by using a standard integral formula for the Gamma function. Find an expression for $h(x)$ by using a standard integral formula for the Beta function. Hence deduce that

  $$\frac{\Gamma(z) \Gamma(w)}{\Gamma(z+w)}=\mathrm{B}(z, w)$$

  for all $\operatorname{Re}(z)>0, \operatorname{Re}(w)>0$.

  comment

• Paper 1, Section II, G

  Algebraic Topology

  Part II, 2016

  Let $T=S^{1} \times S^{1}$ be the 2-dimensional torus. Let $\alpha: S^{1} \rightarrow T$ be the inclusion of the coordinate circle $S^{1} \times\{1\}$, and let $X$ be the result of attaching a 2-cell along $\alpha$.

  (a) Write down a presentation for the fundamental group of $X$ (with respect to some basepoint), and identify it with a well-known group.

  (b) Compute the simplicial homology of any triangulation of $X$.

  (c) Show that $X$ is not homotopy equivalent to any compact surface.

  comment

• Paper 1, Section I, A

  Further Complex Methods

  Part II, 2016

  Evaluate the integral

  $$f(p)=\mathcal{P} \int_{-\infty}^{\infty} d x \frac{e^{i p x}}{x^{4}-1}$$

  where $p$ is a real number, for (i) $p>0$ and (ii) $p<0$.

  comment

• Paper 2, Section I, A

  Further Complex Methods

  Part II, 2016

  The Euler product formula for the Gamma function is

  $$\Gamma(z)=\lim _{n \rightarrow \infty} \frac{n ! n^{z}}{z(z+1) \ldots(z+n)}$$

  Use this to show that

  $$\frac{\Gamma(2 z)}{2^{2 z} \Gamma(z) \Gamma\left(z+\frac{1}{2}\right)}=c,$$

  where $c$ is a constant, independent of $z$. Find the value of $c$.

  comment

• Paper 2, Section II, A

  Further Complex Methods

  Part II, 2016

  The Hurwitz zeta function $\zeta_{\mathrm{H}}(s, q)$ is defined for $\operatorname{Re}(q)>0$ by

  $$\zeta_{\mathrm{H}}(s, q)=\sum_{n=0}^{\infty} \frac{1}{(q+n)^{s}}$$

  State without proof the complex values of $s$ for which this series converges.

  Consider the integral

  $$I(s, q)=\frac{\Gamma(1-s)}{2 \pi i} \int_{\mathcal{C}} d z \frac{z^{s-1} e^{q z}}{1-e^{z}}$$

  where $\mathcal{C}$ is the Hankel contour. Show that $I(s, q)$ provides an analytic continuation of the Hurwitz zeta function for all $s \neq 1$. Include in your account a careful discussion of removable singularities. [Hint: $\Gamma(s) \Gamma(1-s)=\pi / \sin (\pi s)$.]

  Show that $I(s, q)$ has a simple pole at $s=1$ and find its residue.

  comment

• Paper 1, Section II, A

  Further Complex Methods

  Part II, 2016

  (a) Legendre's equation for $w(z)$ is

  $$\left(z^{2}-1\right) w^{\prime \prime}+2 z w^{\prime}-\ell(\ell+1) w=0, \quad \text { where } \quad \ell=0,1,2, \ldots$$

  Let $\mathcal{C}$ be a closed contour. Show by direct substitution that for $z$ within $\mathcal{C}$

  $$\int_{\mathcal{C}} d t \frac{\left(t^{2}-1\right)^{\ell}}{(t-z)^{\ell+1}}$$

  is a non-trivial solution of Legendre's equation.

  (b) Now consider

  $$Q_{\nu}(z)=\frac{1}{4 i \sin \nu \pi} \int_{\mathcal{C}^{\prime}} d t \frac{\left(t^{2}-1\right)^{\nu}}{(t-z)^{\nu+1}}$$

  for real $\nu>-1$ and $\nu \neq 0,1,2, \ldots$. The closed contour $\mathcal{C}^{\prime}$ is defined to start at the origin, wind around $t=1$ in a counter-clockwise direction, then wind around $t=-1$ in a clockwise direction, then return to the origin, without encircling the point $z$. Assuming that $z$ does not lie on the real interval $-1 \leqslant x \leqslant 1$, show by deforming $\mathcal{C}^{\prime}$ onto this interval that functions $Q_{\ell}(z)$ may be defined as limits of $Q_{\nu}(z)$ with $\nu \rightarrow \ell=0,1,2, \ldots$.

  Find an explicit expression for $Q_{0}(z)$ and verify that it satisfies Legendre's equation with $\ell=0$.

  comment

• Paper 2, Section II, H

  Galois Theory

  Part II, 2016

  (a) Let $K \subseteq L$ be a finite separable field extension. Show that there exist only finitely many intermediate fields $K \subseteq F \subseteq L$.

  (b) Define what is meant by a normal extension. Is $\mathbb{Q} \subseteq \mathbb{Q}(\sqrt{1+\sqrt{7}})$ a normal extension? Justify your answer.

  (c) Prove Artin's lemma, which states: if $K \subseteq L$ is a field extension, $H$ is a finite subgroup of $\operatorname{Aut}_{K}(L)$, and $F:=L^{H}$ is the fixed field of $H$, then $F \subseteq L$ is a Galois extension with $\operatorname{Gal}(L / F)=H$.

  comment

• Paper 3, Section II, H

  Galois Theory

  Part II, 2016

  (a) Let $L$ be the 13 th cyclotomic extension of $\mathbb{Q}$, and let $\mu$ be a 13 th primitive root of unity. What is the minimal polynomial of $\mu$ over $\mathbb{Q}$ ? What is the Galois group $\operatorname{Gal}(L / \mathbb{Q})$ ? Put $\lambda=\mu+\frac{1}{\mu}$. Show that $\mathbb{Q} \subseteq \mathbb{Q}(\lambda)$ is a Galois extension and find $\operatorname{Gal}(\mathbb{Q}(\lambda) / \mathbb{Q})$.

  (b) Define what is meant by a Kummer extension. Let $K$ be a field of characteristic zero and let $L$ be the $n$th cyclotomic extension of $K$. Show that there is a sequence of Kummer extensions $K=F_{1} \subseteq F_{2} \subseteq \cdots \subseteq F_{r}$ such that $L$ is contained in $F_{r}$.

  comment

• Paper 1, Section II, H

  Galois Theory

  Part II, 2016

  (a) Prove that if $K$ is a field and $f \in K[t]$, then there exists a splitting field $L$ of $f$ over $K$. [You do not need to show uniqueness of $L$.]

  (b) Let $K_{1}$ and $K_{2}$ be algebraically closed fields of the same characteristic. Show that either $K_{1}$ is isomorphic to a subfield of $K_{2}$ or $K_{2}$ is isomorphic to a subfield of $K_{1}$. [For subfields $F_{i}$ of $K_{1}$ and field homomorphisms $\psi_{i}: F_{i} \rightarrow K_{2}$ with $i=1$, 2, we say $\left(F_{1}, \psi_{1}\right) \leqslant\left(F_{2}, \psi_{2}\right)$ if $F_{1}$ is a subfield of $F_{2}$ and $\left.\psi_{2}\right|_{F_{1}}=\psi_{1}$. You may assume the existence of a maximal pair $(F, \psi)$ with respect to the partial order just defined.]

  (c) Give an example of a finite field extension $K \subseteq L$ such that there exist $\alpha, \beta \in L \backslash K$ where $\alpha$ is separable over $K$ but $\beta$ is not separable over $K .$

  comment

• Paper 4, Section II, H

  Galois Theory

  Part II, 2016

  (a) Let $f=t^{5}-9 t+3 \in \mathbb{Q}[t]$ and let $L$ be the splitting field of $f$ over $\mathbb{Q}$. Show that $\operatorname{Gal}(L / \mathbb{Q})$ is isomorphic to $S_{5}$. Let $\alpha$ be a root of $f$. Show that $\mathbb{Q} \subseteq \mathbb{Q}(\alpha)$ is neither a radical extension nor a solvable extension.

  (b) Let $f=t^{26}+2$ and let $L$ be the splitting field of $f$ over $\mathbb{Q}$. Is it true that $\operatorname{Gal}(L / \mathbb{Q})$ has an element of order 29 ? Justify your answer. Using reduction mod $p$ techniques, or otherwise, show that $\operatorname{Gal}(L / \mathbb{Q})$ has an element of order 3 .

  [Standard results from the course may be used provided they are clearly stated.]

  comment

• Paper 4, Section II, D

  General Relativity

  Part II, 2016

  A spherically symmetric static spacetime has metric

  $$d s^{2}=-\left(1+r^{2} / b^{2}\right) d t^{2}+\frac{d r^{2}}{1+r^{2} / b^{2}}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  where $-\infty<t<\infty, r \geqslant 0, b$ is a positive constant, and units such that $c=1$ are used.

  (a) Explain why a time-like geodesic may be assumed, without loss of generality, to lie in the equatorial plane $\theta=\pi / 2$. For such a geodesic, show that the quantities

  $$E=\left(1+r^{2} / b^{2}\right) \dot{t} \quad \text { and } \quad h=r^{2} \dot{\phi}$$

  are constants of the motion, where a dot denotes differentiation with respect to proper time, $\tau$. Hence find a first-order differential equation for $r(\tau)$.

  (b) Consider a massive particle fired from the origin, $r=0$. Show that the particle will return to the origin and find the proper time taken.

  (c) Show that circular orbits $r=a$ are possible for any $a>0$ and determine whether such orbits are stable. Show that on any such orbit a clock measures coordinate time.

  comment

• Paper 1, Section II, D

  General Relativity

  Part II, 2016

  Consider a family of geodesics with $s$ an affine parameter and $V^{a}$ the tangent vector on each curve. The equation of geodesic deviation for a vector field $W^{a}$ is

  $$\frac{D^{2} W^{a}}{D s^{2}}=R_{b c d}^{a} V^{b} V^{c} W^{d}$$

  where $\frac{D}{D s}$ denotes the directional covariant derivative $V^{b} \nabla_{b}$.

  (i) Show that if

  $$V^{b} \frac{\partial W^{a}}{\partial x^{b}}=W^{b} \frac{\partial V^{a}}{\partial x^{b}}$$

  then $W^{a}$ satisfies $(*)$.

  (ii) Show that $V^{a}$ and $s V^{a}$ satisfy $(*)$.

  (iii) Show that if $W^{a}$ is a Killing vector field, meaning that $\nabla_{b} W_{a}+\nabla_{a} W_{b}=0$, then $W^{a}$ satisfies $(*)$.

  (iv) Show that if $W^{a}=w U^{a}$ satisfies $(*)$, where $w$ is a scalar field and $U^{a}$ is a time-like unit vector field, then

  $$\begin{gathered} \frac{d^{2} w}{d s^{2}}=\left(\Omega^{2}-K\right) w \\ -\frac{D U^{a}}{D s} \frac{D U_{a}}{D s} \quad \text { and } \quad K=R_{a b c d} U^{a} V^{b} V^{c} U^{d} \end{gathered}$$

  $$\begin{aligned} & \text { where } \quad \Omega^{2}=-\frac{D U^{a}}{D s} \frac{D U_{a}}{D s} \text { and } \quad K=R_{a b c d} U^{a} V^{b} V^{c} U^{d} \text {. } \end{aligned}$$

  [You may use: $\nabla_{b} \nabla_{c} X^{a}-\nabla_{c} \nabla_{b} X^{a}=R_{d b c}^{a} X^{d}$ for any vector field $\left.X^{a} .\right]$

  comment

• Paper 4, Section II, G

  Algebraic Topology

  Part II, 2016

  Let $T=S^{1} \times S^{1}$ be the 2-dimensional torus, and let $X$ be constructed from $T$ by removing a small open disc.

  (a) Show that $X$ is homotopy equivalent to $S^{1} \vee S^{1}$.

  (b) Show that the universal cover of $X$ is homotopy equivalent to a tree.

  (c) Exhibit (finite) cell complexes $X, Y$, such that $X$ and $Y$ are not homotopy equivalent but their universal covers $\widetilde{X}, \widetilde{Y}$are.

  [State carefully any results from the course that you use.]

  comment

• Paper 2, Section II, D

  General Relativity

  Part II, 2016

  The Kasner (vacuum) cosmological model is defined by the line element

  $$d s^{2}=-c^{2} d t^{2}+t^{2 p_{1}} d x^{2}+t^{2 p_{2}} d y^{2}+t^{2 p_{3}} d z^{2} \quad \text { with } \quad t>0$$

  where $p_{1}, p_{2}, p_{3}$ are constants with $p_{1}+p_{2}+p_{3}=p_{1}^{2}+p_{2}^{2}+p_{3}^{2}=1$ and $0<p_{1}<1$. Show that $p_{2} p_{3}<0$.

  Write down four equations that determine the null geodesics of the Kasner model.

  If $k^{a}$ is the tangent vector to the trajectory of a photon and $u^{a}$ is the four-velocity of a comoving observer (i.e., an observer at rest in the $(t, x, y, z)$ coordinate system above), what is the physical interpretation of $k_{a} u^{a}$ ?

  Let $O$ be a comoving observer at the origin, $x=y=z=0$, and let $S$ be a comoving source of photons located on one of the spatial coordinate axes.

  (i) Show that photons emitted by $S$ and observed by $O$ can be either redshifted or blue-shifted, depending on the location of $S$.

  (ii) Given any fixed time $t=T$, show that there are locations for $S$ on each coordinate axis from which no photons reach $O$ for $t \leqslant T$.

  Now suppose that $p_{1}=1$ and $p_{2}=p_{3}=0$. Does the property in (ii) still hold?

  comment

• Paper 3, Section II, D

  General Relativity

  Part II, 2016

  For a spacetime that is nearly flat, the metric $g_{a b}$ can be expressed in the form

  $$g_{a b}=\eta_{a b}+h_{a b}$$

  where $\eta_{a b}$ is a flat metric (not necessarily diagonal) with constant components, and the components of $h_{a b}$ and their derivatives are small. Show that

  $$2 R_{b d} \approx h_{d}^{a}, b a+h_{b}^{a}, d a-h_{a, b d}^{a}-h_{b d, a c} \eta^{a c}$$

  where indices are raised and lowered using $\eta_{a b}$.

  [You may assume that $\left.R_{b c d}^{a}=\Gamma_{b d, c}^{a}-\Gamma_{b c, d}^{a}+\Gamma_{c e}^{a} \Gamma_{d b}^{e}-\Gamma_{d e}^{a} \Gamma_{c b}^{e} .\right]$

  For the line element

  $$d s^{2}=2 d u d v+d x^{2}+d y^{2}+H(u, x, y) d u^{2},$$

  where $H$ and its derivatives are small, show that the linearised vacuum field equations reduce to $\nabla^{2} H=0$, where $\nabla^{2}$ is the two-dimensional Laplacian operator in $x$ and $y$.

  comment

• Paper 3, Section II, G

  Graph Theory

  Part II, 2016

  Define the chromatic polynomial $p_{G}(t)$ of a graph $G$. Show that if $G$ has $n$ vertices and $m$ edges then

  $$p_{G}(t)=a_{n} t^{n}-a_{n-1} t^{n-1}+a_{n-2} t^{n-2}-\ldots+(-1)^{n} a_{0}$$

  where $a_{n}=1, a_{n-1}=m$ and $a_{i} \geqslant 0$ for all $i$. [You may assume the deletion-contraction relation, provided that you state it clearly.]

  Show that for every graph $G$ (with $n>0$ ) we have $a_{0}=0$. Show also that $a_{1}=0$ if and only if $G$ is disconnected.

  Explain why $t^{4}-2 t^{3}+3 t^{2}-t$ is not the chromatic polynomial of any graph.

  comment

• Paper 2, Section II, G

  Graph Theory

  Part II, 2016

  Define the Turán graph $T_{r}(n)$, where $r$ and $n$ are positive integers with $n \geqslant r$. For which $r$ and $n$ is $T_{r}(n)$ regular? For which $r$ and $n$ does $T_{r}(n)$ contain $T_{4}(8)$ as a subgraph?

  State and prove Turán's theorem.

  Let $x_{1}, \ldots, x_{n}$ be unit vectors in the plane. Prove that the number of pairs $i<j$ for which $x_{i}+x_{j}$ has length less than 1 is at most $\left\lfloor n^{2} / 4\right\rfloor$.

  comment

• Paper 4, Section II, G

  Graph Theory

  Part II, 2016

  State Menger's theorem in both the vertex form and the edge form. Explain briefly how the edge form of Menger's theorem may be deduced from the vertex form.

  (a) Show that if $G$ is 3 -connected then $G$ contains a cycle of even length.

  (b) Let $G$ be a connected graph with all degrees even. Prove that $\lambda(G)$ is even. [Hint: if $S$ is a minimal set of edges whose removal disconnects $G$, let $H$ be a component of $G-S$ and consider the degrees of the vertices of $H$ in the graph $G-S$.] Give an example to show that $\kappa(G)$ can be odd.

  comment

• Paper 1, Section II, 16G

  Graph Theory

  Part II, 2016

  (a) Show that if $G$ is a planar graph then $\chi(G) \leqslant 5$. [You may assume Euler's formula, provided that you state it precisely.]

  (b) (i) Prove that if $G$ is a triangle-free planar graph then $\chi(G) \leqslant 4$.

  (ii) Prove that if $G$ is a planar graph of girth at least 6 then $\chi(G) \leqslant 3$.

  (iii) Does there exist a constant $g$ such that, if $G$ is a planar graph of girth at least $g$, then $\chi(G) \leqslant 2 ?$ Justify your answer.

  comment

• Paper 3, Section II, D

  Integrable Systems

  Part II, 2016

  What is meant by an auto-Bäcklund transformation?

  The sine-Gordon equation in light-cone coordinates is

  $$\frac{\partial^{2} \varphi}{\partial \xi \partial \tau}=\sin \varphi$$

  where $\xi=\frac{1}{2}(x-t), \tau=\frac{1}{2}(x+t)$ and $\varphi$ is to be understood modulo $2 \pi$. Show that the pair of equations

  $$\partial_{\xi}\left(\varphi_{1}-\varphi_{0}\right)=2 \epsilon \sin \left(\frac{\varphi_{1}+\varphi_{0}}{2}\right), \quad \partial_{\tau}\left(\varphi_{1}+\varphi_{0}\right)=\frac{2}{\epsilon} \sin \left(\frac{\varphi_{1}-\varphi_{0}}{2}\right)$$

  constitute an auto-Bäcklund transformation for (1).

  By noting that $\varphi=0$ is a solution to (1), use the transformation (2) to derive the soliton (or 'kink') solution to the sine-Gordon equation. Show that this solution can be expressed as

  $$\varphi(x, t)=4 \arctan \left[\exp \left(\pm \frac{x-c t}{\sqrt{1-c^{2}}}+x_{0}\right)\right]$$

  for appropriate constants $c$ and $x_{0}$.

  [Hint: You may use the fact that $\int \operatorname{cosec} x \mathrm{~d} x=\log \tan (x / 2)+$ const.]

  The following function is a solution to the sine-Gordon equation:

  $$\varphi(x, t)=4 \arctan \left[c \frac{\sinh \left(x / \sqrt{1-c^{2}}\right)}{\cosh \left(c t / \sqrt{1-c^{2}}\right)}\right] \quad(c>0) .$$

  Verify that this represents two solitons travelling towards each other at the same speed by considering $x \pm c t=$ constant and taking an appropriate limit.

  comment

• Paper 1, Section II, D

  Integrable Systems

  Part II, 2016

  What does it mean for an evolution equation $u_{t}=K\left(x, u, u_{x}, \ldots\right)$ to be in Hamiltonian form? Define the associated Poisson bracket.

  An evolution equation $u_{t}=K\left(x, u, u_{x}, \ldots\right)$ is said to be bi-Hamiltonian if it can be written in Hamiltonian form in two distinct ways, i.e.

  $$K=\mathcal{J} \delta H_{0}=\mathcal{E} \delta H_{1}$$

  for Hamiltonian operators $\mathcal{J}, \mathcal{E}$ and functionals $H_{0}, H_{1}$. By considering the sequence $\left\{H_{m}\right\}_{m \geqslant 0}$ defined by the recurrence relation

  $$\mathcal{E} \delta H_{m+1}=\mathcal{J} \delta H_{m}$$

  show that bi-Hamiltonian systems possess infinitely many first integrals in involution. [You may assume that $(*)$ can always be solved for $H_{m+1}$, given $H_{m}$.]

  The Harry Dym equation for the function $u=u(x, t)$ is

  $$u_{t}=\frac{\partial^{3}}{\partial x^{3}}\left(u^{-1 / 2}\right)$$

  This equation can be written in Hamiltonian form $u_{t}=\mathcal{E} \delta H_{1}$ with

  $$\mathcal{E}=2 u \frac{\partial}{\partial x}+u_{x}, \quad H_{1}[u]=\frac{1}{8} \int u^{-5 / 2} u_{x}^{2} \mathrm{~d} x$$

  Show that the Harry Dym equation possesses infinitely many first integrals in involution. [You need not verify the Jacobi identity if your argument involves a Hamiltonian operator.]

  comment

• Paper 2, Section II, D

  Integrable Systems

  Part II, 2016

  What does it mean for $g^{\epsilon}:(x, u) \mapsto(\tilde{x}, \tilde{u})$ to describe a 1-parameter group of transformations? Explain how to compute the vector field

  $$V=\xi(x, u) \frac{\partial}{\partial x}+\eta(x, u) \frac{\partial}{\partial u}$$

  that generates such a 1-parameter group of transformations.

  Suppose now $u=u(x)$. Define the $n$th prolongation, $\mathrm{pr}^{(n)} g^{\epsilon}$, of $g^{\epsilon}$ and the vector field which generates it. If $V$ is defined by $(*)$ show that

  $$\mathrm{pr}^{(n)} V=V+\sum_{k=1}^{n} \eta_{k} \frac{\partial}{\partial u^{(k)}}$$

  where $u^{(k)}=\mathrm{d}^{k} u / \mathrm{d} x^{k}$ and $\eta_{k}$ are functions to be determined.

  The curvature of the curve $u=u(x)$ in the $(x, u)$-plane is given by

  $$\kappa=\frac{u_{x x}}{\left(1+u_{x}^{2}\right)^{3 / 2}}$$

  Rotations in the $(x, u)$-plane are generated by the vector field

  $$W=x \frac{\partial}{\partial u}-u \frac{\partial}{\partial x}$$

  Show that the curvature $\kappa$ at a point along a plane curve is invariant under such rotations. Find two further transformations that leave $\kappa$ invariant.

  comment

• Paper 3, Section II, I

  Linear Analysis

  Part II, 2016

  (a) Define Banach spaces and Euclidean spaces over $\mathbb{R}$. [You may assume the definitions of vector spaces and inner products.]

  (b) Let $X$ be the space of sequences of real numbers with finitely many non-zero entries. Does there exist a norm $\|\cdot\|$ on $X$ such that $(X,\|\cdot\|)$ is a Banach space? Does there exist a norm such that $(X,\|\cdot\|)$ is Euclidean? Justify your answers.

  (c) Let $(X,\|\cdot\|)$ be a normed vector space over $\mathbb{R}$ satisfying the parallelogram law

  $$\|x+y\|^{2}+\|x-y\|^{2}=2\|x\|^{2}+2\|y\|^{2}$$

  for all $x, y \in X$. Show that $\langle x, y\rangle=\frac{1}{4}\left(\|x+y\|^{2}-\|x-y\|^{2}\right)$ is an inner product on $X$. [You may use without proof the fact that the vector space operations $+$ and are continuous with respect to $\|\cdot\|$. To verify the identity $\langle a+b, c\rangle=\langle a, c\rangle+\langle b, c\rangle$, you may find it helpful to consider the parallelogram law for the pairs $(a+c, b),(b+c, a),(a-c, b)$ and $(b-c, a) .]$

  (d) Let $\left(X,\|\cdot\|_{X}\right)$ be an incomplete normed vector space over $\mathbb{R}$ which is not a Euclidean space, and let $\left(X^{*},\|\cdot\|_{X^{*}}\right)$ be its dual space with the dual norm. Is $\left(X^{*},\|\cdot\|_{X^{*}}\right)$ a Banach space? Is it a Euclidean space? Justify your answers.

  comment

• Paper 1, Section II, A

  Applications of Quantum Mechanics

  Part II, 2016

  A particle in one dimension of mass $m$ and energy $E=\hbar^{2} k^{2} / 2 m(k>0)$ is incident from $x=-\infty$ on a potential $V(x)$ with $V(x) \rightarrow 0$ as $x \rightarrow-\infty$ and $V(x)=\infty$ for $x>0$. The relevant solution of the time-independent Schrödinger equation has the asymptotic form

  $$\psi(x) \sim \exp (i k x)+r(k) \exp (-i k x), \quad x \rightarrow-\infty$$

  Explain briefly why a pole in the reflection amplitude $r(k)$ at $k=i \kappa$ with $\kappa>0$ corresponds to the existence of a stable bound state in this potential. Indicate why a pole in $r(k)$ just below the real $k$-axis, at $k=k_{0}-i \rho$ with $k_{0} \gg \rho>0$, corresponds to a quasi-stable bound state. Find an approximate expression for the lifetime $\tau$ of such a quasi-stable state.

  Now suppose that

  $$V(x)= \begin{cases}\left(\hbar^{2} U / 2 m\right) \delta(x+a) & \text { for } x<0 \\ \infty & \text { for } x>0\end{cases}$$

  where $U>0$ and $a>0$ are constants. Compute the reflection amplitude $r(k)$ in this case and deduce that there are quasi-stable bound states if $U$ is large. Give expressions for the wavefunctions and energies of these states and compute their lifetimes, working to leading non-vanishing order in $1 / U$ for each expression.

  [ You may assume $\psi=0$ for $x \geqslant 0$ and $\lim _{\epsilon \rightarrow 0+}\left\{\psi^{\prime}(-a+\epsilon)-\psi^{\prime}(-a-\epsilon)\right\}=U \psi(-a)$.]

  comment

• Paper 2, Section II, I

  Linear Analysis

  Part II, 2016

  (a) Let $K$ be a topological space and let $C_{\mathbb{R}}(K)$ denote the normed vector space of bounded continuous real-valued functions on $K$ with the norm $\|f\|_{C_{\mathbb{R}}(K)}=\sup _{x \in K}|f(x)|$. Define the terms uniformly bounded, equicontinuous and relatively compact as applied to subsets $S \subset C_{\mathbb{R}}(K)$.

  (b) The Arzela-Ascoli theorem [which you need not prove] states in particular that if $K$ is compact and $S \subset C_{\mathbb{R}}(K)$ is uniformly bounded and equicontinuous, then $S$ is relatively compact. Show by examples that each of the compactness of $K$, uniform boundedness of $S$, and equicontinuity of $S$ are necessary conditions for this conclusion.

  (c) Let $L$ be a topological space. Assume that there exists a sequence of compact subsets $K_{n}$ of $L$ such that $K_{1} \subset K_{2} \subset K_{3} \subset \cdots \subset L$ and $\bigcup_{n=1}^{\infty} K_{n}=L$. Suppose $S \subset C_{\mathbb{R}}(L)$ is uniformly bounded and equicontinuous and moreover satisfies the condition that, for every $\epsilon>0$, there exists $n \in \mathbb{N}$ such that $|f(x)|<\epsilon$ for every $x \in L \backslash K_{n}$ and for every $f \in S$. Show that $S$ is relatively compact.

  comment

• Paper 1, Section II, I

  Linear Analysis

  Part II, 2016

  (a) State the closed graph theorem.

  (b) Prove the closed graph theorem assuming the inverse mapping theorem.

  (c) Let $X, Y, Z$ be Banach spaces and $T: X \rightarrow Y, S: Y \rightarrow Z$ be linear maps. Suppose that $S \circ T$ is bounded and $S$ is both bounded and injective. Show that $T$ is bounded.

  comment

• Paper 4, Section II, I

  Linear Analysis

  Part II, 2016

  Let $H$ be a complex Hilbert space.

  (a) Let $T: H \rightarrow H$ be a bounded linear map. Show that the spectrum of $T$ is a subset of $\left\{\lambda \in \mathbb{C}:|\lambda| \leqslant\|T\|_{\mathcal{B}(H)}\right\}$.

  (b) Let $T: H \rightarrow H$ be a bounded self-adjoint linear map. For $\lambda, \mu \in \mathbb{C}$, let $E_{\lambda}:=\{x \in H: T x=\lambda x\}$ and $E_{\mu}:=\{x \in H: T x=\mu x\}$. If $\lambda \neq \mu$, show that $E_{\lambda} \perp E_{\mu}$.

  (c) Let $T: H \rightarrow H$ be a compact self-adjoint linear map. For $\lambda \neq 0$, show that $E_{\lambda}:=\{x \in H: T x=\lambda x\}$ is finite-dimensional.

  (d) Let $H_{1} \subset H$ be a closed, proper, non-trivial subspace. Let $P$ be the orthogonal projection to $H_{1}$.

  (i) Prove that $P$ is self-adjoint.

  (ii) Determine the spectrum $\sigma(P)$ and the point spectrum $\sigma_{p}(P)$ of $P$.

  (iii) Find a necessary and sufficient condition on $H_{1}$ for $P$ to be compact.

  comment

• Paper 2, Section II, F

  Logic and Set Theory

  Part II, 2016

  Define the von Neumann hierarchy of sets $V_{\alpha}$, and show that each $V_{\alpha}$ is a transitive set. Explain what is meant by saying that a binary relation on a set is well-founded and extensional. State Mostowski's Theorem.

  Let $r$ be the binary relation on $\omega$ defined by: $\langle m, n\rangle \in r$ if and only if $2^{m}$ appears in the base-2 expansion of $n$ (i.e., the unique expression for $n$ as a sum of distinct powers of 2 ). Show that $r$ is well-founded and extensional. To which transitive set is $(\omega, r)$ isomorphic? Justify your answer.

  comment

• Paper 3, Section II, F

  Logic and Set Theory

  Part II, 2016

  State the Completeness Theorem for the first-order predicate calculus, and deduce the Compactness Theorem.

  Let $\mathbb{T}$ be a first-order theory over a signature $\Sigma$ whose axioms all have the form $(\forall \vec{x}) \phi$ where $\vec{x}$is a (possibly empty) string of variables and $\phi$ is quantifier-free. Show that every substructure of a $\mathbb{T}$-model is a $\mathbb{T}$-model, and deduce that if $\mathbb{T}$ is consistent then it has a model in which every element is the interpretation of a closed term of $\mathcal{L}(\Sigma)$. $[$ You may assume the result that if $B$ is a substructure of $A$ and $\phi$ is a quantifier-free formula with $n$ free variables, then $\llbracket \phi \rrbracket_{B}=\llbracket \phi \rrbracket_{A} \cap B^{n}$.]

  Now suppose $\mathbb{T} \vdash(\exists x) \psi$ where $\psi$ is a quantifier-free formula with one free variable $x$. Show that there is a finite list $\left(t_{1}, t_{2}, \ldots, t_{n}\right)$ of closed terms of $\mathcal{L}(\Sigma)$ such that

  $$\mathbb{T} \vdash\left(\psi\left[t_{1} / x\right] \vee \psi\left[t_{2} / x\right] \vee \cdots \vee \psi\left[t_{n} / x\right]\right)$$

  comment

• Paper 1, Section II, F

  Logic and Set Theory

  Part II, 2016

  Which of the following statements are true? Justify your answers. (a) Every ordinal is of the form $\alpha+n$, where $\alpha$ is a limit ordinal and $n \in \omega$. (b) Every ordinal is of the form $\omega^{\alpha} \cdot m+n$, where $\alpha$ is an ordinal and $m, n \in \omega$. (c) If $\alpha=\omega \cdot \alpha$, then $\alpha=\omega^{\omega} \cdot \beta$ for some $\beta$. (d) If $\alpha=\omega^{\alpha}$, then $\alpha$ is uncountable. (e) If $\alpha>1$ and $\alpha=\alpha^{\omega}$, then $\alpha$ is uncountable.

  [Standard laws of ordinal arithmetic may be assumed, but if you use the Division Algorithm you should prove it.]

  comment

• Paper 4, Section II, F

  Logic and Set Theory

  Part II, 2016

  (a) State Zorn's Lemma, and use it to prove that every nontrivial distributive lattice $L$ admits a lattice homomorphism $L \rightarrow\{0,1\}$.

  (b) Let $S$ be a propositional theory in a given language $\mathcal{L}$. Sketch the way in which the equivalence classes of formulae of $\mathcal{L}$, modulo $S$-provable equivalence, may be made into a Boolean algebra. [Detailed proofs are not required, but you should define the equivalence relation explicitly.]

  (c) Hence show how the Completeness Theorem for propositional logic may be deduced from the result of part (a).

  comment

• Paper 4, Section I, B

  Mathematical Biology

  Part II, 2016

  A stochastic birth-death process is given by the master equation

  $$\frac{d p_{n}}{d t}=\lambda\left(p_{n-1}-p_{n}\right)+\mu\left[(n-1) p_{n-1}-n p_{n}\right]+\beta\left[(n+1) p_{n+1}-n p_{n}\right]$$

  where $p_{n}(t)$ is the probability that there are $n$ individuals in the population at time $t$ for $n=0,1,2, \ldots$ and $p_{n}=0$ for $n<0$. Give a brief interpretation of $\lambda, \mu$ and $\beta$.

  Derive an equation for $\frac{\partial \phi}{\partial t}$, where $\phi$ is the generating function

  $$\phi(s, t)=\sum_{n=0}^{\infty} s^{n} p_{n}(t)$$

  Now assume that $\beta>\mu$. Show that at steady state

  $$\phi=\left(\frac{\beta-\mu}{\beta-\mu s}\right)^{\lambda / \mu}$$

  and find the corresponding mean and variance.

  comment

• Paper 3, Section $\mathbf{I}$, B

  Mathematical Biology

  Part II, 2016

  A delay model for a population of size $N_{t}$ at discrete time $t$ is given by

  $$N_{t+1}=\max \left\{\left(r-N_{t-1}^{2}\right) N_{t}, 0\right\}$$

  Show that for $r>1$ there is a non-trivial equilibrium, and analyse its stability. Show that, as $r$ is increased from 1 , the equilibrium loses stability at $r=3 / 2$ and find the approximate periodicity close to equilibrium at this point.

  comment

• Paper 2, Section I, B

  Mathematical Biology

  Part II, 2016

  (a) The populations of two competing species satisfy

  $$\begin{aligned} \frac{d N_{1}}{d t} &=N_{1}\left[b_{1}-\lambda\left(N_{1}+N_{2}\right)\right] \\ \frac{d N_{2}}{d t} &=N_{2}\left[b_{2}-\lambda\left(N_{1}+N_{2}\right)\right] \end{aligned}$$

  where $b_{1}>b_{2}>0$ and $\lambda>0$. Sketch the phase diagram (limiting attention to $\left.N_{1}, N_{2} \geqslant 0\right)$.

  The relative abundance of species 1 is defined by $U=N_{1} /\left(N_{1}+N_{2}\right)$. Show that

  $$\frac{d U}{d t}=A U(1-U)$$

  where $A$ is a constant that should be determined.

  (b) Consider the spatial system

  $$\frac{\partial u}{\partial t}=u(1-u)+D \frac{\partial^{2} u}{\partial x^{2}}$$

  and consider a travelling-wave solution of the form $u(x, t)=f(x-c t)$ representing one species $(u=1)$ invading territory previously occupied by another species $(u=0)$. By linearising near the front of the invasion, show that the wave speed is given by $c=2 \sqrt{D}$.

  [You may assume that the solution to the full nonlinear system will settle to the slowest possible linear wave speed.]

  comment

• Paper 3, Section II, A

  Applications of Quantum Mechanics

  Part II, 2016

  (a) A spinless charged particle moves in an electromagnetic field defined by vector and scalar potentials $\mathbf{A}(\mathbf{x}, t)$ and $\phi(\mathbf{x}, t)$. The wavefunction $\psi(\mathbf{x}, t)$ for the particle satisfies the time-dependent Schrödinger equation with Hamiltonian

  $$\hat{H}_{0}=\frac{1}{2 m}(-i \hbar \boldsymbol{\nabla}+e \mathbf{A}) \cdot(-i \hbar \boldsymbol{\nabla}+e \mathbf{A})-e \phi .$$

  Consider a gauge transformation

  $$\mathbf{A} \rightarrow \tilde{\mathbf{A}}=\mathbf{A}+\nabla f, \quad \phi \rightarrow \tilde{\phi}=\phi-\frac{\partial f}{\partial t}, \quad \psi \rightarrow \tilde{\psi}=\exp \left(-\frac{i e f}{\hbar}\right) \psi$$

  for some function $f(\mathbf{x}, t)$. Define covariant derivatives with respect to space and time, and show that $\tilde{\psi}$ satisfies the Schrödinger equation with potentials $\tilde{\mathbf{A}}$ and $\tilde{\phi}$.

  (b) Suppose that in part (a) the magnetic field has the form $\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}=(0,0, B)$, where $B$ is a constant, and that $\phi=0$. Find a suitable $\mathbf{A}$ with $A_{y}=A_{z}=0$ and determine the energy levels of the Hamiltonian $\hat{H}_{0}$ when the $z$-component of the momentum of the particle is zero. Suppose in addition that the particle is constrained to lie in a rectangular region of area $\mathcal{A}$ in the $(x, y)$-plane. By imposing periodic boundary conditions in the $x$-direction, estimate the degeneracy of each energy level. [You may use without proof results for a quantum harmonic oscillator, provided they are clearly stated.]

  (c) An electron is a charged particle of spin $\frac{1}{2}$ with a two-component wavefunction $\psi(\mathbf{x}, t)$ governed by the Hamiltonian

  $$\hat{H}=\hat{H}_{0} \mathbb{I}_{2}+\frac{e \hbar}{2 m} \mathbf{B} \cdot \boldsymbol{\sigma}$$

  where $\mathbb{I}_{2}$ is the $2 \times 2$ unit matrix and $\sigma=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ denotes the Pauli matrices. Find the energy levels for an electron in the constant magnetic field defined in part (b), assuming as before that the $z$-component of the momentum of the particle is zero.

  Consider $N$ such electrons confined to the rectangular region defined in part (b). Ignoring interactions between the electrons, show that the ground state energy of this system vanishes for $N$ less than some integer $N_{\max }$ which you should determine. Find the ground state energy for $N=(2 p+1) N_{\max }$, where $p$ is a positive integer.

  comment

• Paper 1, Section I, B

  Mathematical Biology

  Part II, 2016

  Consider an epidemic model where susceptibles are vaccinated at per capita rate $v$, but immunity (from infection or vaccination) is lost at per capita rate $b$. The system is given by

  $$\begin{aligned} &\frac{d S}{d t}=-r I S+b(N-I-S)-v S \\ &\frac{d I}{d t}=r I S-a I \end{aligned}$$

  where $S(t)$ are the susceptibles, $I(t)$ are the infecteds, $N$ is the total population size and all parameters are positive. The basic reproduction ratio $R_{0}=r N / a$ satisfies $R_{0}>1$.

  Find the critical vaccination rate $v_{c}$, in terms of $b$ and $R_{0}$, such that the system has an equilibrium with the disease present if $v<v_{c}$. Show that this equilibrium is stable when it exists.

  Find the long-term outcome for $S$ and $I$ if $v>v_{c}$.

  comment

• Paper 3, Section II, B

  Mathematical Biology

  Part II, 2016

  The Fitzhugh-Nagumo model is given by

  $$\begin{aligned} \dot{u} &=c\left(v+u-\frac{1}{3} u^{3}+z(t)\right) \\ \dot{v} &=-\frac{1}{c}(u-a+b v) \end{aligned}$$

  where $\left(1-\frac{2}{3} b\right)<a<1,0<b \leqslant 1$ and $c \gg 1$.

  For $z(t)=0$, by considering the nullclines in the $(u, v)$-plane, show that there is a unique equilibrium. Sketch the phase diagram

  At $t=0$ the system is at the equilibrium, and $z(t)$ is then 'switched on' to be $z(t)=-V_{0}$ for $t>0$, where $V_{0}$ is a constant. Describe carefully how suitable choices of $V_{0}>0$ can represent a system analogous to (i) a neuron firing once, and (ii) a neuron firing repeatedly. Illustrate your answer with phase diagrams and also plots of $v$ against $t$ for each case. Find the threshold for $V_{0}$ that separates these cases. Comment briefly from a biological perspective on the behaviour of the system when $a=1-\frac{2}{3} b+\epsilon b$ and $0<\epsilon \ll 1$.

  comment

• Paper 4, Section II, B

  Mathematical Biology

  Part II, 2016

  The population densities of two types of cell are given by $U(x, t)$ and $V(x, t)$. The system is described by the equations

  $$\begin{aligned} \frac{\partial U}{\partial t} &=\alpha U(1-U)+\chi \frac{\partial}{\partial x}\left(U \frac{\partial V}{\partial x}\right)+D \frac{\partial^{2} U}{\partial x^{2}} \\ \frac{\partial V}{\partial t} &=V(1-V)-\beta U V+\frac{\partial^{2} V}{\partial x^{2}} \end{aligned}$$

  where $\alpha, \beta, \chi$ and $D$ are positive constants.

  (a) Identify the terms which involve interaction between the cell types, and briefly describe what each of these terms might represent.

  (b) Consider the system without spatial dynamics. Find the condition on $\beta$ for there to be a non-trivial spatially homogeneous solution that is stable to spatially invariant disturbances.

  (c) Consider now the full spatial system, and consider small spatial perturbations proportional to $\cos (k x)$ of the solution found in part (b). Show that for sufficiently large $\chi$ (the precise threshold should be found) the spatially homogeneous solution is stable to perturbations with either small or large wavenumber, but is unstable to perturbations at some intermediate wavenumber.

  comment

• Paper 2, Section II, F

  Number Fields

  Part II, 2016

  (a) Prove that $5+2 \sqrt{6}$ is a fundamental unit in $\mathbb{Q}(\sqrt{6})$. [You may not assume the continued fraction algorithm.]

  (b) Determine the ideal class group of $\mathbb{Q}(\sqrt{-55})$.

  comment

• Paper 1, Section II, F

  Number Fields

  Part II, 2016

  (a) Let $f(X) \in \mathbb{Q}[X]$ be an irreducible polynomial of degree $n, \theta \in \mathbb{C}$ a root of $f$, and $K=\mathbb{Q}(\theta)$. Show that $\operatorname{disc}(f)=\pm N_{K / \mathbb{Q}}\left(f^{\prime}(\theta)\right)$.

  (b) Now suppose $f(X)=X^{n}+a X+b$. Write down the matrix representing multiplication by $f^{\prime}(\theta)$ with respect to the basis $1, \theta, \ldots, \theta^{n-1}$ for $K$. Hence show that

  $$\operatorname{disc}(f)=\pm\left((1-n)^{n-1} a^{n}+n^{n} b^{n-1}\right)$$

  (c) Suppose $f(X)=X^{4}+X+1$. Determine $\mathcal{O}_{K}$. [You may quote any standard result, as long as you state it clearly.]

  comment

• Paper 4, Section II, F

  Number Fields

  Part II, 2016

  Let $K$ be a number field, and $p$ a prime in $\mathbb{Z}$. Explain what it means for $p$ to be inert, to split completely, and to be ramified in $K$.

  (a) Show that if $[K: \mathbb{Q}]>2$ and $\mathcal{O}_{K}=\mathbb{Z}[\alpha]$ for some $\alpha \in K$, then 2 does not split completely in $K$.

  (b) Let $K=\mathbb{Q}(\sqrt{d})$, with $d \neq 0,1$ and $d$ square-free. Determine, in terms of $d$, whether $p=2$ splits completely, is inert, or ramifies in $K$. Hence show that the primes which ramify in $K$ are exactly those which divide $D_{K}$.

  comment

• Paper 3, Section I, I

  Number Theory

  Part II, 2016

  Show that the exact power of a prime $p$ dividing $N !$ is $\sum_{j=1}^{\infty}\left\lfloor\frac{N}{p^{j}}\right\rfloor$. By considering the prime factorisation of $\left(\begin{array}{c}2 n \\ n\end{array}\right)$, show that

  $$\frac{4^{n}}{2 n+1} \leqslant\left(\begin{array}{c} 2 n \\ n \end{array}\right) \leqslant(2 n)^{\pi(2 n)}$$

  Setting $n=\left\lfloor\frac{x}{2}\right\rfloor$, deduce that for $x$ sufficiently large

  $$\pi(x)>\frac{\left\lfloor\frac{x}{2}\right\rfloor \log 3}{\log x}>\frac{x}{2 \log x}$$

  comment

• Paper 4 , Section I, I

  Number Theory

  Part II, 2016

  Compute the continued fraction expansion of $\sqrt{14}$, and use it to find two solutions to $x^{2}-14 y^{2}=2$ where $x$ and $y$ are positive integers.

  comment

• Paper 2, Section I, I

  Number Theory

  Part II, 2016

  Define the Legendre symbol and the Jacobi symbol. Compute the Jacobi symbols $\left(\frac{202}{11189}\right)$ and $\left(\frac{974}{1001}\right)$, stating clearly any properties of these symbols that you use.

  comment

• Paper 1, Section I, I

  Number Theory

  Part II, 2016

  Define the Riemann zeta function $\zeta(s)$ for $\operatorname{Re}(s)>1$. State and prove the alternative formula for $\zeta(s)$ as an Euler product. Hence or otherwise show that $\zeta(s) \neq 0$ for $\operatorname{Re}(s)>1$.

  comment