Paper 1, Section II, K
(a) Let be an -vector of responses from the linear model , with . The internally studentized residual is defined by
where is the least squares estimate, is the leverage of sample , and
Prove that the joint distribution of is the same in the following two models: (i) , and (ii) , with (in this model, are identically -distributed). [Hint: A random vector is spherically symmetric if for any orthogonal matrix . If is spherically symmetric and a.s. nonzero, then is a uniform point on the sphere; in addition, any orthogonal projection of is also spherically symmetric. A standard normal vector is spherically symmetric.]
(b) A social scientist regresses the income of 120 Cambridge graduates onto 20 answers from a questionnaire given to the participants in their first year. She notices one questionnaire with very unusual answers, which she suspects was due to miscoding. The sample has a leverage of . To check whether this sample is an outlier, she computes its externally studentized residual,
where is estimated from a fit of all samples except the one in question, . Is this a high leverage point? Can she conclude this sample is an outlier at a significance level of ?
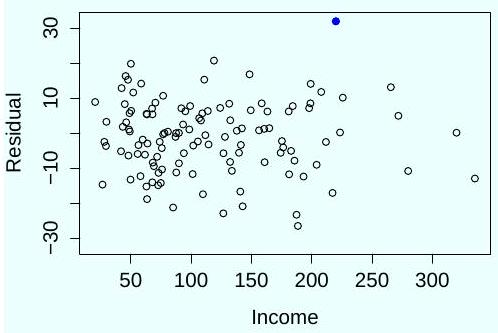
(c) After examining the following plot of residuals against the response, the investigator calculates the externally studentized residual of the participant denoted by the black dot, which is . Can she conclude this sample is an outlier with a significance level of ?
Part II, List of Questions