Paper 3, Section II, K
Part II, 2016
Consider the following two-period market model. There is a risk-free asset which pays interest at rate . There is also a risky stock with prices given by
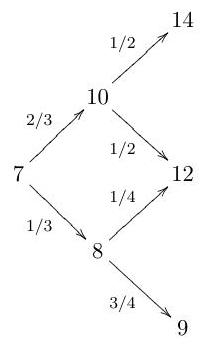
The above diagram should be read as
and so forth.
(a) Find the risk-neutral probabilities.
(b) Consider a European put option with strike expiring at time . What is the initial no-arbitrage price of the option? How many shares should be held in each period to replicate the payout?
(c) Now consider an American put option with the same strike and expiration date. Find the optimal exercise policy, assuming immediate exercise is not allowed. Would your answer change if you were allowed to exercise the option at time 0 ?