Paper 2, Section II, 15C
(a) Show how the -qubit state
can be generated from a computational basis state of by the action of Hadamard gates.
(b) Prove that , where denotes the controlled- gate. Justify (without any explicit calculations) the following identity:
(c) Consider the following two-qubit circuit:
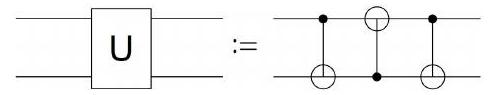
What is its action on an arbitrary 2-qubit state In particular, for two given states and , find the states and such that
(d) Consider the following quantum circuit diagram
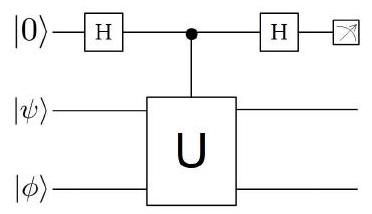
where the measurement is relative to the computational basis and is the quantum gate from part (c). Note that the second gate in the circuit performs the following controlled operation:
(i) Give expressions for the joint state of the three qubits after the action of the first Hadamard gate; after the action of the quantum gate ; and after the action of the second Hadamard gate.
(ii) Compute the probabilities and of getting outcome 0 and 1 , respectively, in the measurement.
(iii) How can the above circuit be used to determine (with high probability) whether the two states and are identical or not? [Assume that you are given arbitrarily many copies of the three input states and that the quantum circuit can be used arbitrarily many times.]