Paper 2, Section II, 21F
Part II, 2021
(a) State a suitable version of the Seifert-van Kampen theorem and use it to calculate the fundamental groups of the torus and of the real projective plane .
(b) Show that there are no covering maps or .
(c) Consider the following covering space of :
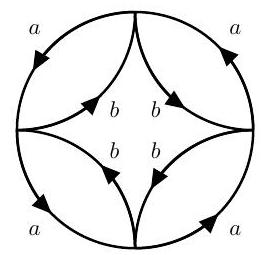
Here the line segments labelled and are mapped to the two different copies of contained in , with orientations as indicated.
Using the Galois correspondence with basepoints, identify a subgroup of
(where is the wedge point) that corresponds to this covering space.